HP Extrapolator - indicador para MetaTrader 4

Autor: gpwr

A qualidade distintiva do filtro de Hodrick-Prescott é que ele não tem atrasos. É calculado minimizando a função objetivo

F = Sum((y[i] - x[i])^2,i=0..n-1) + lambda*Sum((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)

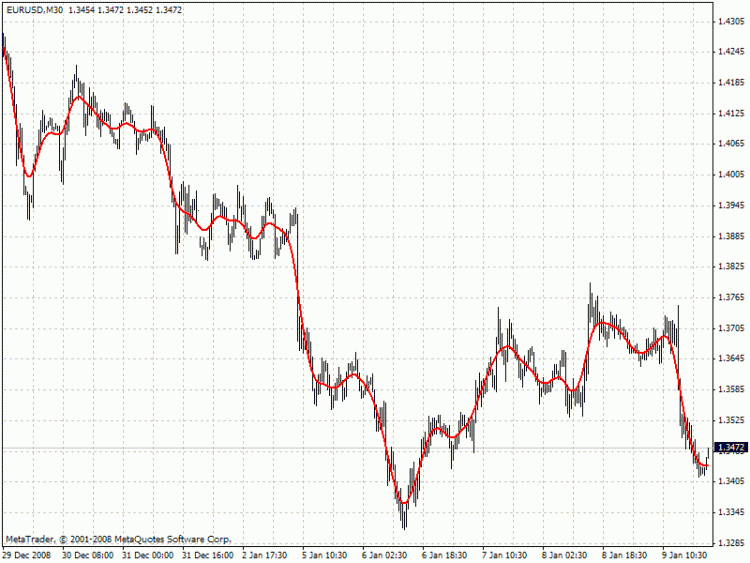
onde x[] é o preço, y[] é o valor do filtro. Aqui está um exemplo do comportamento desse filtro (ver o arquivo anexado HP.mq4)

Se o filtro Hodrick-Prescott olha para o futuro, que valores futuros poderá sugerir? Para responder a esta pergunta, precisamos encontrar um filtro HP digital cuja caraterística seja semelhante ao filtro de Hodrick-Prescott, mas cujos valores são calculados diretamente utilizando valores passados dos preços e valores passados do mesmo "filtro gêmeo", ou seja,

y[i] = Sum(a[k]*x[i-k],k=0..nx-1) - filtro FIR

ou

y[i] = Sum(a[k]*x[i-k],k=0..nx-1) + Sum(b[k]*y[i-k],k=1..ny) - filtro IIR

De preferência, escolha um "filtro gêmeo" que tenha uma latência de freqüência independente CGD (constant group delay). Os filtros IIR, neste caso, não são adequados. Para filtros FIR, a latência de freqüência independente não é uma condição

a[i] = +/-a[nx-1-i], i = 0..nx-1

A Simple Moving Average (SMA) é um filtro FIR com uma latência constante:

y[i] = Sum(x[i-k],k=0..nx-1)/nx

Quanto o nx é impar, a latência desse filtro é igual à CGD = (nx-1)/2. Se deslocar o valor deste filtro SMA, para o passado, no número de barras igual à latência CDG, então, o valor SMA coincidirá com o valor do filtro Hodrick-Prescott. Devido à diferença significativa nas caraterísticas de freqüência dos dois filtros ilustrados neste gráfico, será impossível conseguir uma coincidência exata

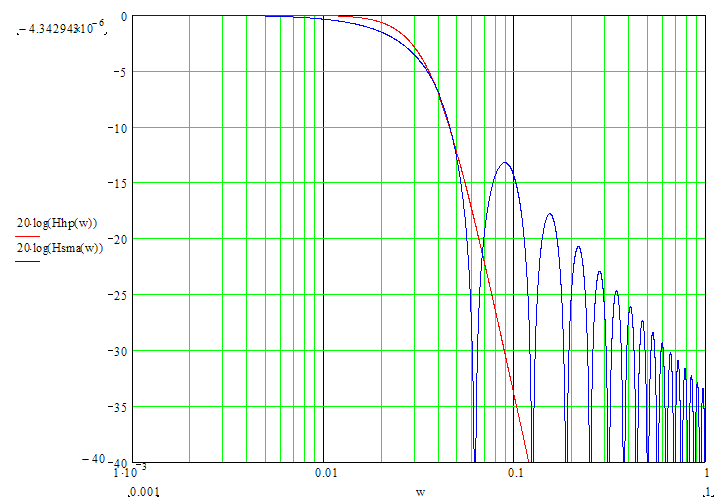
Para conseguir a maior coincidência entre os valores de ambos os filtros, é desejável escolher uma largura da transmissão (por exemplo, no nível -6dB) igual. A largura da transmissão no nível -6dB do filtro Hodrick-Prescott é calculado de acordo com a fórmula

wc = 2*arcsin(0.5/lambda^0.25).

A largura da transmissão no nível -6dB para o filtro SMA acha-se usando métodos numéricos a partir da equação

|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5

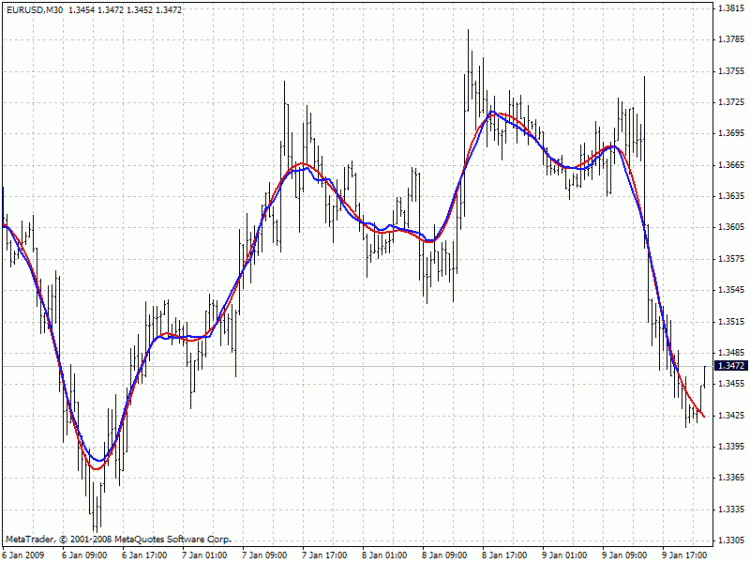
O gráfico abaixo compara os valores de dois filtros com a mesma largura de banda: vermelho para o filtro Hodrick-Prescott (FiltPer = 25), azul para o SMA (Period = 15, Shift = -7). Observe que o SMA (azul) para as últimas 7 barras não existe, pois ele precisa de conhecer os preços futuros. Por sua vez, a filtro Hodrick-Prescott (vermelho)mostra certos valores. Se assumirmos que ao aparecer os preços futuros, o SMA deslocado repetirá os valores do filtro Hodrick-Prescott nas últimas 7 barras, então, quais serão esses valores no futuro?

Algoritmos de previsão:

O indicador dispões de dois métodos de previsão:

Metod 1:

1. Estabelecemos o comprimento SMA igual a 3 e deslocamos o SMA para o passado 1 barra. Tendo tal comprimento, o SMA deslocado não existe apenas para a última barra (Bar = 0), pois ele precisa de o valor do seguinte preço futuro Close[-1].

2. Calculamos a freqüência de transmissão SMA. Nivelamos essa freqüência com a freqüência de transmissão do filtro Hodrick-Prescott. Encontramos lambda.

3. Calculamos o valor do filtro Hodrick-Prescott na última barra HP[0] e assumimos que SMA[0] com um desconhecido Close[-1] dá tal valor.

4. Encontramos Close[-1] = 3*HP[0] - Close[0] - Close[1]

5. Aumentamos o comprimento SMA até 5. Repetimos todos os cálculos e encontramos Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]. E assim por diante até que seja calculado o número de preços futuros FutBars estabelecido.

Metod 2:

1. Estabelecemos o comprimento SMA igual a 2*FutBars+1 e deslocamos SMA para o passado tantos FutBars

2. Calculamos a freqüência de transmissão SMA. Nivelamos essa freqüência com a freqüência de transmissão do filtro Hodrick-Prescott. Encontramos lambda.

3. Calculamos o valor do filtro Hodrick-Prescott nas últimas barras FutBars e assumimos que SMA se comportará do mesmo modo ao aparecer novos preços.

4. Encontramos Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Sum(Close[i],i=0..2*FutBars-1), Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Sum(Close[i],i=-1..2*FutBars-2), etc.

No indicador os seguintes dados de entrada:

Method - metodo de previsão

LastBar - número da última barra para verificar a previsão nos preços existentes (LastBar >= 0)

PastBars - quantidade de barras passadas para as quais será calculado o filtro Hodrick-Prescott (quanto mais, melhor, pelo menos, PastBars>2*FutBars)

FutBars - quantidade de valores futuros previstos

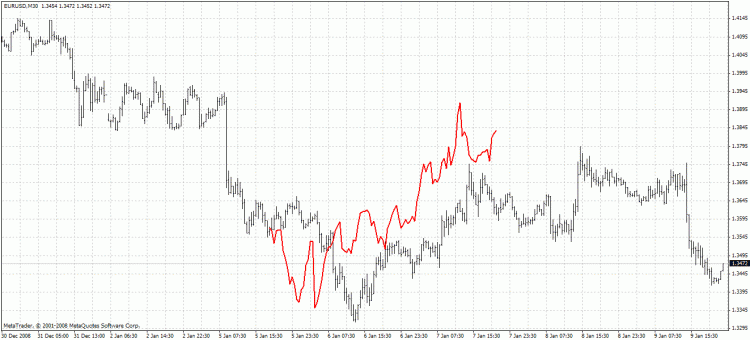
O indicador vermelho representa os valores previstos. No exemplo a seguir usa-se Metod 1:

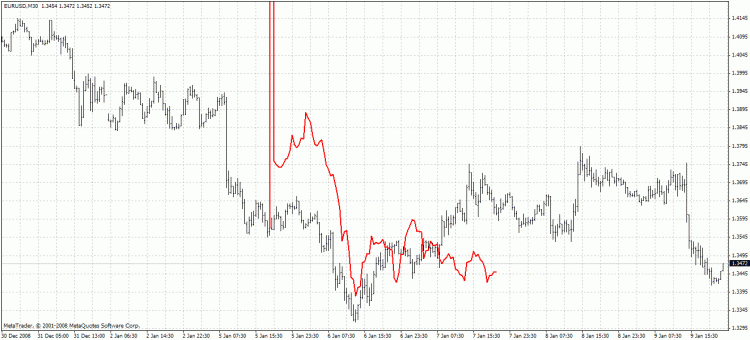
Metod 2:

O segundo método tende a ter previsões mais precisas, mas muitas vezes surgem muitas informações do primeiro preço previsto. O método de previsão pode ser melhorado usando o filtro FIR com uma caraterística de freqüência mais próxima do filtro Hodrick- Prescott. Por exemplo, em vez de SMA, é possível experimentar Hanning, Blackman, Kaiser e outro filtros com uma latência constante.

O autor agradece ao Korey, pela publicação do indicador para construir o filtro Hodrick-Prescott, no seguinte tópico do fórum:

https://www.mql5.com/ru/forum/113677/page2