HP Extrapolator - индикатор для MetaTrader 4

Автор: gpwr

Отличительное качество фильтра Ходрика-Прескота в том что он не имеет задержки. Рассчитывается он путём минимизации целевой функции

F = Sum((y[i] - x[i])^2,i=0..n-1) + lambda*Sum((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)

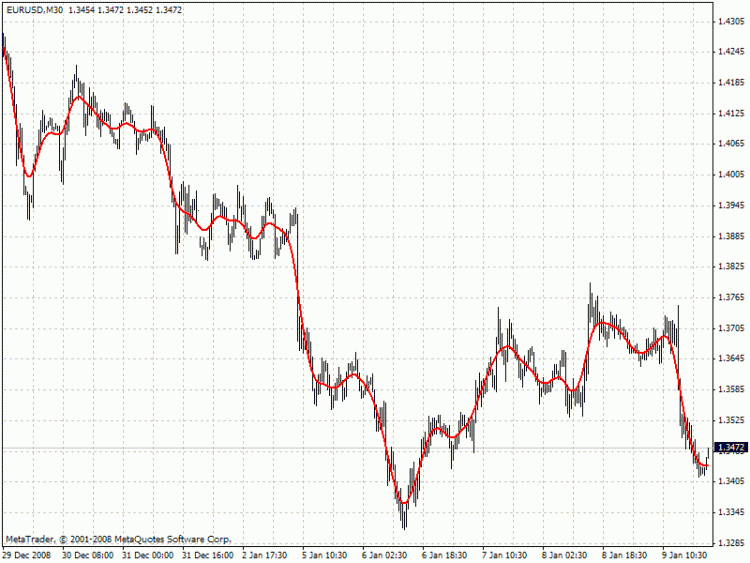
где x[] - цены, y[] - значения фильтра. Вот пример поведения этого фильтра (см приложенный файл HP.mq4)

Если фильтр Ходрика-Прескота заглядывает в будущее, то какие будущие значения он предполагает? Чтобы ответить на этот вопрос, нужно найти цифровой НЧ фильтр, частотная характеристика которого похожа на ту фильтра Ходрика-Прескота, но значения которого рассчитываются напрямую используя прошлые значения цены и прошлые значения самого "фильтра-близнеца", т.е.

y[i] = Sum(a[k]*x[i-k],k=0..nx-1) - FIR фильтр

или

y[i] = Sum(a[k]*x[i-k],k=0..nx-1) + Sum(b[k]*y[i-k],k=1..ny) - IIR фильтр

Предпочтительно выбрать такой "фильтр-близнец", который имел бы частотно-независимую задержку Тзад (constant group delay). IIR фильтры в таком случае не подходят. Для FIR фильтров, условием частотно-независимой задержки является

a[i] = +/-a[nx-1-i], i = 0..nx-1

Простейшим FIR фильтром с постоянной задержкой является Simple Moving Average (SMA):

y[i] = Sum(x[i-k],k=0..nx-1)/nx

При нечётном nx, задержка такого фильтра равна Тзад = (nx-1)/2. Если сдвинуть значения этого SMA фильтра в прошлое на количество баров равному задержке Тзад, то SMA значения совпадут со значениями фильтра Ходрика-Прескота. Точного совпадения достичь невозможно из-за существенной разницы в частотных характеристик двух фильтров проиллюстрированной на этом графике

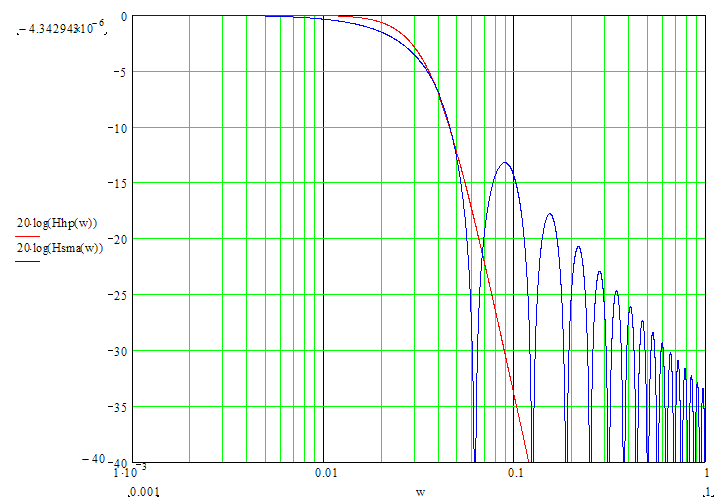
Чтобы достичь наиболее близкого совпадения между значениями обоих фильтров, желательно выбрать их ширину пропускания (например, на уровне -6dB) одинаковой. Ширина пропускания на уровне -6dB фильтра Ходрика-Прескота расчитывается по формуле

wc = 2*arcsin(0.5/lambda^0.25).

Ширина пропускания на уровне -6dB для SMA фильтра находится численными методами из уравнения

|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5

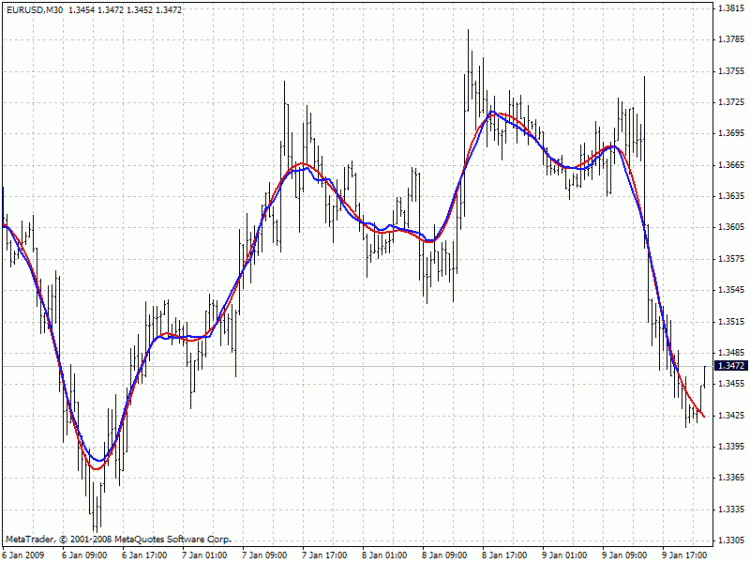
График внизу сравнивает значения двух фильтров при одинаковой полосе пропускания: красный цвет - фильтр Ходрика-Прескота (FiltPer = 25), синий цвет - SMA (Period = 15, Shift = -7). Заметьте что SMA (синий) для последних 7 баров не существует, т.к. ему нужно знать будущие цены. Фильтр Ходрика-Прескота (красный), с другой стороны, показывает какие-то значения. Если предположить что при появлении будущих цен, сдвинутый SMA будет повторять значения фильтра Ходрика-Прескота на последних 7 барах, то какие эти будущие значения должны быть?

Алгоритмы предсказания:

В индикаторе встроены два метода предсказания:

Metod 1:

1. Задаём длинну SMA равную 3 и сдвигаем SMA в прошлое на 1 бар. При такой длинне, сдвинутый SMA не существует только для последнего бара (Bar = 0), т.к. ему нужно значение следующей будущей цены Close[-1].

2. Рассчитываем частоту пропускания SMA. Приравниваем эту частоту к частоте пропускания фильтра Ходрика-Прескота. Находим lambda.

3. Рассчитываем значение фильтра Ходрика-Прескота на последнем баре HP[0] и предполагаем что SMA[0] с неизвестной Close[-1] даёт такое же значение.

4. Находим Close[-1] = 3*HP[0] - Close[0] - Close[1]

5. Увеличиваем длинну SMA до 5. Повторяем все вычисления и находим Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]. И так далее пока не рассчитано заданное количество будущих цен FutBars.

Metod 2:

1. Задаём длинну SMA равную 2*FutBars+1 и сдвигаем SMA в прошлое на FutBars

2. Рассчитываем частоту пропускания SMA. Приравниваем эту частоту к частоте пропускания фильтра Ходрика-Прескота. Находим lambda.

3. Рассчитываем значения фильтра Ходрика-Прескота на последних FutBars барах и предполагаем что SMA поведёт себя таким же образом при появлении новых цен.

4. Находим Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Sum(Close[i],i=0..2*FutBars-1), Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Sum(Close[i],i=-1..2*FutBars-2), и т.д.

В индикаторе следующие входные данные:

Method - метод предсказания

LastBar - номер последнего бара для проверки предсказания на существуящих ценах (LastBar >= 0)

PastBars - количество прошлых баров для которых будет рассчитываться фильтр Ходрика-Прескотта (чем больше тем лучше или, по крайней мере, PastBars>2*FutBars)

FutBars - количество предсказанных будущих значений

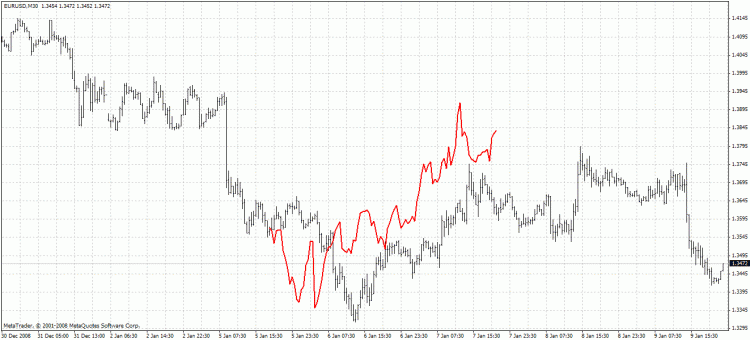
Индикатор красным цветом строит предсказанные значения. В следующем примере используется Metod 1:

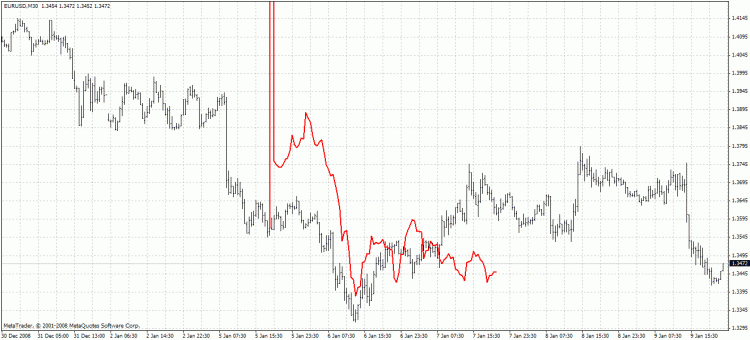
Metod 2:

Второй метод имеет тенденцию более точного предсказания, но часто имеет большие выбросы первой предсказанной цены. Описанный метод предсказания может улучшен путём нахождения FIR фильтра с частотной характеристикой более близкой к той фильтра Ходрика-Прескота. Например, вместо SMA, можно попробовать Hanning, Blackman, Kaiser и другие фильтры с постоянной задержкой.

Автор благодарен Korey за публикацию оригинального индикатора построения фильтра Ходрика-Прескота в следующей ветке форума:

https://www.mql5.com/ru/forum/113677/page2