Raise Your Linear Trading Systems to the Power
9 080
14
Introduction
Today's article shows intermediate MQL5 programmers how they can get more profit from their linear trading systems (Fixed Lot) by easily implementing the so-called technique of exponentiation. The general term of exponentiation is used here for referring to those monetary management models that adapt the size or the number of the positions placed in the market according to the risk that one takes. This is because the resulting equity curve growth is then geometric, or exponential, taking the form of a parabola. The term "linear" is also used in the present context which is halfway between the mathematical and the programming one. Specifically, we will implement a practical MQL5 variant of the Fixed Fractional position sizing developed by Ralph Vince.
Figure 1. Mathematical parabola
Let's do now a quick summary of Money Management Models and see how we can implement a variant of Ralph Vince's Fixed Fractional position sizing. Are you ready? Do not miss the opportunity to get much more from your trading strategies!
1. What Are Money Management Models?
In a nutshell, Money Management Models are the conceptual frameworks, under which you take decisions in relation to your position sizings, the use of your stop losses, and your margin calculations and trading costs. There are many Money Management Models out there! If you wish, you can google for Fixed Lot, Fixed Fractional, Fixed Ratio, Kelly's Percentage or Effective Cost to deepen your knowledge on those classical frameworks. As I say, this article only covers a variant of Fixed Fractional.
1.2. Fixed Fractional
The idea behind this money management model is sizing operations according to the estimated risk associated to them. The risk is the same fraction of the net on each trade.
The equation for the number of contracts in fixed fractional position sizing is as follows:
N = f * Equity / Trade Risk
N is the number of contracts, f is the fixed fraction (a number between 0 and 1), Equity is the current value of account equity, and Trade Risk is the risk of the trade per contract for which the number of contracts is being computed. Please, read the article Fixed Fractional Position Sizing written by Michael R. Bryant to learn more about this model.
An interesting property of Fixed Fractional model is that since the size of the operations is maintained proportional to the net balance of the account, it is theoretically impossible to lose all your capital. The risk of ruin is zero. On the other hand, as risk capital percentages are lower, a streak of winning or losing operations do not have a dramatic impact on the profit curve.
2. Adding Fixed Fractional to Your Trading System
2.1. Take Your Linear Trading System
Of course, first of all you need a linear trading system to experience the low risk exponential power! This system will serve as the power base, so to speak. By a linear system I mean a trading system which proves to be a winner for a certain period of time and whose equity curve looks like a straight line. For example, HawaiianTsunamiSurfer is a so-called linear trading system available in Code Base. Its equity curve looks like a straight line from January 2012 to March 2012.
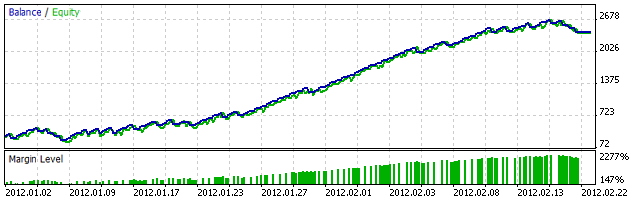
Figure 2. HawaiianTsunamiSurfer's equity curve from January 2012 to March 2012
The aim of this article is not to develop a linear trading system from scratch, but to give you the necessary tools so that you can get more juice from your systems. So from now on, I will assume that you have already developed a trading system like this under the object-oriented paradigm. In this case, you should add the OO piece, which I explain below.
2.2. CEvolution, the Core MQL5 Class to Raise Your System to the Power
So once again we take the object-oriented approach to code our EA. I recommend you first read the articles Another MQL5 OOP class and Building an Automatic News Trader to get the technical basis for working this OO way. If you have already done this, keep in mind that the designs discussed in those articles incorporate a very important element named CEvolution. This allows us keeping track of some important temporal information such as the status of the robot at a given moment, the history of the operations performed, etc.
This time we will code in CEvolution the logic required to manage our money. As the risked fixed fraction stays proportional to the equity, in which we all agree it is not constant, but variable, this logical stuff must be coded in CEvolution. Or simply put, as the equity curve slope evolves with time it is in CEvolution where all this stuff must be implemented. This is our object-oriented design's abstract idea. It is left as an exercise for you integrating the following OO class with your object-oriented styled trading system.
Class CEvolution.mqh:
//+------------------------------------------------------------------+ //| CEvolution.mqh | //| Copyright © 2013, Jordi Bassagañas | //+------------------------------------------------------------------+ #include <Mine\Enums.mqh> //+------------------------------------------------------------------+ //| CEvolution Class | //+------------------------------------------------------------------+ class CEvolution { protected: ENUM_STATUS_EA m_status; // The current EA's status ENUM_EXP_EQUITY_CURVE_LEVEL m_expEquityLevel; // The current exponential equity level double m_originalEquity; // The original equity value double m_lotSize; // The current lot size public: //--- Constructor and destructor methods CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level); ~CEvolution(void); //--- Getter methods ENUM_STATUS_EA GetStatus(void); ENUM_EXP_EQUITY_CURVE_LEVEL GetExpEquityLevel(void); double GetOriginalEquity(void); double GetLotSize(void); //--- Setter methods void SetStatus(ENUM_STATUS_EA status); void SetExpEquityLevel(ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level); void SetOriginalEquity(double equity); void SetLotSize(double size); //--- CEvolution specific methods double CalcEquityGrowth(double currentEquity); void RefreshExpEquityLevel(double currentEquity); void RefreshLotSize(); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CEvolution::CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level) { m_status=status; m_expEquityLevel=exp_equity_level; RefreshLotSize(); m_originalEquity=AccountInfoDouble(ACCOUNT_EQUITY); } //+------------------------------------------------------------------+ //| Destructor | //+------------------------------------------------------------------+ CEvolution::~CEvolution(void) { } //+------------------------------------------------------------------+ //| GetStatus | //+------------------------------------------------------------------+ ENUM_STATUS_EA CEvolution::GetStatus(void) { return m_status; } //+------------------------------------------------------------------+ //| GetExpEquityLevel | //+------------------------------------------------------------------+ ENUM_EXP_EQUITY_CURVE_LEVEL CEvolution::GetExpEquityLevel(void) { return m_expEquityLevel; } //+------------------------------------------------------------------+ //| GetEquity | //+------------------------------------------------------------------+ double CEvolution::GetOriginalEquity(void) { return m_originalEquity; } //+------------------------------------------------------------------+ //| GetLotSize | //+------------------------------------------------------------------+ double CEvolution::GetLotSize(void) { return m_lotSize; } //+------------------------------------------------------------------+ //| SetStatus | //+------------------------------------------------------------------+ void CEvolution::SetStatus(ENUM_STATUS_EA status) { m_status=status; } //+------------------------------------------------------------------+ //| SetExpEquityLevel | //+------------------------------------------------------------------+ void CEvolution::SetExpEquityLevel(ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level) { m_expEquityLevel=exp_equity_level; } //+------------------------------------------------------------------+ //| SetEquity | //+------------------------------------------------------------------+ void CEvolution::SetOriginalEquity(double equity) { m_originalEquity=equity; } //+------------------------------------------------------------------+ //| SetLotSize | //+------------------------------------------------------------------+ void CEvolution::SetLotSize(double lot_size) { m_lotSize=lot_size; } //+------------------------------------------------------------------+ //| CalcEquityGrowth | //+------------------------------------------------------------------+ double CEvolution::CalcEquityGrowth(double currentEquity) { return NormalizeDouble(currentEquity * 100 / m_originalEquity - 100,2); } //+------------------------------------------------------------------+ //| RefreshExpEquityLevel | //+------------------------------------------------------------------+ void CEvolution::RefreshExpEquityLevel(double currentEquity) { double growth = CalcEquityGrowth(currentEquity); //--- is the current equity less than 10% of the original amount? if(growth <= 10) { SetExpEquityLevel(LEVEL_ONE); } //--- is the current equity more than 10% of the original amount and less than 20%? else if(growth > 10 && growth <= 20) { SetExpEquityLevel(LEVEL_TWO); } //--- is the current equity more than 20% of the original amount and less than 30%? else if(growth > 20 && growth <= 30) { SetExpEquityLevel(LEVEL_THREE); } //--- is the current equity more than 30% of the original amount and less than 40%? else if(growth > 30 && growth <= 40) { SetExpEquityLevel(LEVEL_FOUR); } //--- is the current equity more than 40% of the original amount and less than 50%? else if(growth > 40 && growth <= 50) { SetExpEquityLevel(LEVEL_FIVE); } //--- is the current equity more than 50% of the original amount and less than 60%? else if(growth > 50 && growth <= 60) { SetExpEquityLevel(LEVEL_SEVEN); } //--- is the current equity more than 60% of the original amount and less than 70%? else if(growth > 60 && growth <= 70) { SetExpEquityLevel(LEVEL_EIGHT); } //--- is the current equity more than 70% of the original amount and less than 80%? else if(growth > 70 && growth <= 80) { SetExpEquityLevel(LEVEL_NINE); } //--- is the current equity more than 90% of the original amount? else if(growth > 90) { SetExpEquityLevel(LEVEL_TEN); } } //+------------------------------------------------------------------+ //| RefreshLotSize | //+------------------------------------------------------------------+ void CEvolution::RefreshLotSize() { switch(m_expEquityLevel) { case LEVEL_ONE: SetLotSize(0.01); break; case LEVEL_TWO: SetLotSize(0.02); break; case LEVEL_THREE: SetLotSize(0.03); break; case LEVEL_FOUR: SetLotSize(0.04); break; case LEVEL_FIVE: SetLotSize(0.05); break; case LEVEL_SIX: SetLotSize(0.06); break; case LEVEL_SEVEN: SetLotSize(0.07); break; case LEVEL_EIGHT: SetLotSize(0.08); break; case LEVEL_NINE: SetLotSize(0.09); break; case LEVEL_TEN: SetLotSize(0.1); break; } } //+------------------------------------------------------------------+
Let's now comment some important parts of this class!
When the Expert Advisor is created, the value of the original equity curve is stored in m_originalEquity:
//+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CEvolution::CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level) { m_status=status; m_expEquityLevel=exp_equity_level; RefreshLotSize(); m_originalEquity=AccountInfoDouble(ACCOUNT_EQUITY); }
The method CEvolution::CalcEquityGrowth is for calculating the equity curve's growth, always with respect to its original value:
//+------------------------------------------------------------------+ //| CalcEquityGrowth | //+------------------------------------------------------------------+ double CEvolution::CalcEquityGrowth(double currentEquity) { return NormalizeDouble(currentEquity * 100 / m_originalEquity - 100,2); }
Finally, CEvolution::RefreshExpEquityLevel is for refreshing the equity level on every tick (observe how it absolutely depends on the equity growth) and CEvolution::RefreshLotSize is for refreshing the lot size on every tick. This is because you are supposed to refresh that info in your EA's OnTick method this way:
GetEvolution().RefreshExpEquityLevel(AccountInfoDouble(ACCOUNT_EQUITY)); GetEvolution().RefreshLotSize();
By the way, this solution requires the use of the following custom MQL5 enumeration:
//+------------------------------------------------------------------+ //| Exponential equity curve level enumeration | //+------------------------------------------------------------------+ enum ENUM_EXP_EQUITY_CURVE_LEVEL { LEVEL_ONE, LEVEL_TWO, LEVEL_THREE, LEVEL_FOUR, LEVEL_FIVE, LEVEL_SIX, LEVEL_SEVEN, LEVEL_EIGHT, LEVEL_NINE, LEVEL_TEN };We say this implementation is a variant of Fixed Fractional because indeed it introduces some specificities. For example, the equity curve will grow exponentially until reaching the so-called level ten, thereafter the system will become linear. Nevertheless, CEvolution retains the basic idea of constantly increasing the size of the positions in proportion to the equity curve.
2.3. Taking Your Fixed Fractional Decisions
With all the above, you can already take your money management decisions based on the current status of your robot.
Somewhere in your EA's OnTick method:
switch(GetEvolution().GetStatus()) { case BUY: tp = ask + m_takeProfit * _Point; sl = bid - m_stopLoss * _Point; GetTrade().PositionOpen(GetBrain().GetSymbol(),ORDER_TYPE_BUY,m_evolution.GetLotSize(),ask,sl,tp); break; case SELL: sl = ask + m_takeProfit * _Point; tp = bid - m_stopLoss * _Point; GetTrade().PositionOpen(GetBrain().GetSymbol(),ORDER_TYPE_SELL,m_evolution.GetLotSize(),bid,sl,tp); break; case DO_NOTHING: // Nothing... break; }
I have renamed my new exponentiated system to ExponentialHawaiian.
3. Backtesting your exponentiated system
Once you add the OO logic explained above to your system, do not forget to run your tests! Now I am backtesting ExponentialHawaiian, the Fixed Fractional variant of HawaiianTsunamiSurfer:
Figure 3. ExponentialHawaiian's equity curve from January 2012 to March 2012
The curve above will remain exponential while the underlying system remains linear. When this condition is no longer true, the system becomes unstable with a theoretical risk of ruin.
Conclusion
Today we have learnt how to get more profit from our linear trading systems, those implementing a Fixed Lot money management model, by raising them to the power of exponentiation.
We began by presenting some classical money management models (Fixed Lot, Fixed Fractional, Fixed Ratio, Kelly's Percentage, Effective Cost) and decided to focus on Fixed Fractional, a simple model in which the size of the operations is maintained proportional to the net balance of the account. Finally, we took a trading system showing linear results for a period of time, we implemented in MQL5 a variant of Fixed Fractional, and showed the results launched by MetaTrader's Strategy Tester.
Once again, we have taken the object-oriented approach to code our Expert Advisors. It is highly recommended you first read the articles Another MQL5 OOP class and Building an Automatic News Trader to get the technical basis for working this OO way.
Visual Optimization of Indicator and Signal Profitability
MQL5 Cookbook: Indicator Subwindow Controls - Scrollbar
Advanced Analysis of a Trading Account
MQL5 Cookbook: Indicator Subwindow Controls - Buttons
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Okay, you are a good reader so let's delve into this topic a bit deeper! I want you to think.
You're thinking that trading is like mathematics, however my article opens a door for you to work your critical faculties, as you are doing now. IMHO, trading requires that for you. It is actually absurd that you raise any system to the power and make you a millionaire! In that case, we would all be rich.
The funny thing here is that the base theory remains true. That's why I say: "Once you add the OO logic explained above to your system, do not forget to run your tests! Now I am backtesting ExponentialHawaiian, the Fixed Fractional variant of HawaiianTsunamiSurfer".
This sentence above is true. So strictly speaking, let me say that maybe you made a wrong logical deduction. I don't want the reader to think that he/she will be a millionaire by raising any linear trading system to the power. I encourage you to take CEvolution together with your system and observe your own results. That's trading!, I think.
Funny thing is that if you have studied Edward Thorp, not Vince, you would know that a fixed fraction may not be suitable for all strategies, because under certain circumstances, you need a lot of transactions, before it will get better results.
See: Edward O. Thorp. The Kelly Criterion in Blackjack,Sports,Betting, And The Stock Market
Read more here: 4. The Long Run: When Will The Kelly Strategy "Dominate''?
You cannot apply a fixed fraction for any strategy. Since it does not always give better results than other strategies for managing capital and risk.
E. Thorp is a good mathematician, gamblers and experienced trader. He earned his practice.
R. Vince - theorist, not a practitioner. He earns incorrectly copying other people's ideas in his books, and receiving royalties for them.
Vince's followers often make mistakes, which have long been known to practice trading, but about which nothing is said in the books of Vince. They try to apply mathematical methods where they can not be used.
I threw the books of Vince, because they have a lot of inaccuracies and of little practical use.
In my opinion, it is not a good idea to show the advantage of an innovation by showing results on a 3-month test. If I were to compare it, I'd compare it over a 10-year period.
By scaling a price chart (or even a random walk) with a non-linear function (exponent, simply and clearly) you can make a "grail" TS in one or two times. Such scaling ultimately comes down to managing position size. But the whole problem is that the market is discrete: you have a minimum lot and there is a minimum price movement (pip). Eventually, in these discrete sections, all non-linearity degenerates into linearity.
I'm talking without taking into account the commission and spread -- such an abstract price line for long-term investors)).