MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português
preview
多层感知器和反向传播算法（第二部分）：利用 Python 实现并与 MQL5 集成

多层感知器和反向传播算法（第二部分）：利用 Python 实现并与 MQL5 集成

MetaTrader 5 — 示例 | 23 十一月 2021, 13:58
4 498 9
Jonathan Pereira
Jonathan Pereira

概述

上一篇文章研究了如何创建一个简单的神经元（感知器）。 我们学习了梯度下降法、由互连感知器组成的多层感知器 (MLP) 网络的构建，以及如何训练此类网络。

在本文中，我想演示利用 Python 语言实现这种算法类型是多么容易。

有一个 Python 程序包可用于开发与 MQL 的集成，它提供了大量机会，例如数据探索、创建和使用机器学习模型。

集成在 MQL5 内置的 Python，能够创建各种解决方案，从简单的线性回归、到深度学习模型。 由于这种语言是为专业用途而设计的，因此有许多函数库可以执行与艰难计算相关的任务。

我们将手工创建一个网络。 但正如我在上一篇文章中提到的，这只是帮助我们理解在学习和预测过程中实际发生事件的一个步骤。 然后我将展示一个利用 TensorFlow 和 Keras 的更复杂的例子。


什么是 TensorFlow？

TensorFlow 是一个快速数值处理的开源函数库。

它是由 Google 依照 Apache 开源许可下创建、支持和发布。 该 API 是为 Python 语言设计的，尽管它也可以访问基本的 C++ API。

与设计用于深度学习的其它数字函数库（例如 Theano）不同，TensorFlow 意在研究和生产。 例如，Google 用到的基于机器学习的搜索引擎 RankBrain，和一个非常有趣的计算机视觉项目 DeepDream。

它可以在一个 CPU、GPU 或小型移动设备上的系统中运行，也可在由数百台计算机组成的大型分布式系统中运行。

 

什么是 Keras？

Keras 是一个功能强大，且易于使用的开源 Python 函数库，用于开发和评估深度学习模型。

它涉及强大的 Theano 和 TensorFlow 计算函数库。 它能够在短短几行代码中定义和训练神经网络模型。

教程

本教程分为 4 个章节：

  1. 在 MetaEditor 中安装和准备 Python 环境。
  2. 初期步骤和模型重建（感知器和 MLP）。
  3. 利用 Keras 和 TensorFlow 创建一个简单的模型。
  4. 如何集成 MQL5 和 Python。


1. 安装和准备 Python 环境。

首先，您应该从官方网站 www.python.org/downloads/ 下载 Python

为了使用 TensorFlow，您应该安装 3.3 和 3.8 之间的版本（我个人使用 3.7）。

下载并开始安装过程后，选中 “Add Python 3.7 to PATH” 选项。 这可确保某些事情马上就能工作，且无需以后额外配置。

然后可以直接从 MetaTrader 5 终端轻松运行 Python 脚本。

  • 定义 Python 可执行路径（环境）
  • 安装项目所需的依赖部件 

打开 MetaEditor，并进入“工具\选项”。

在此处指定 Python 可执行文件所在的路径。 注意，安装后它应该有默认的 Python 路径。 如果没有，则需手工输入可执行文件的完整路径。 如此即可令您直接从 MetaTrader 5 终端运行脚本。

1 - 配置编译器

我个人使用一个完全独立的函数库环境，称为虚拟环境。 这是一种获得“干净”安装并仅收集产品所需的库的方法。

有关 venv 包的更多信息，请阅读此处。


一旦完毕，您就能够直接从终端运行 Python 脚本。 对于这个项目，我们需要安装以下函数库。

如果您不确定如何安装这些库，请参阅相关的模块安装指南。

  • MetaTrader 5
  • TensorFlow
  • Matplotlib
  • Pandas
  • Sklearn

现在，我们已经安装并配置好了环境，下面我们来进行一个小测试，了解如何在终端中创建和运行一个小脚本。 为了直接从 MetaEditor 启动新脚本，请按照以下步骤操作：

新建 > Python 脚本

1 - 新建脚本

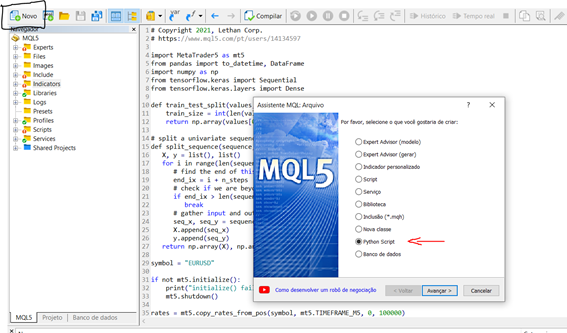
为您的脚本指定名称。 MetaEditor 中的 MQL 向导会自动提示您需要导入一些函数库。 这很有趣，且对于我们的实验，我们要选择 Numpy 选项。

3 - 新建脚本 II

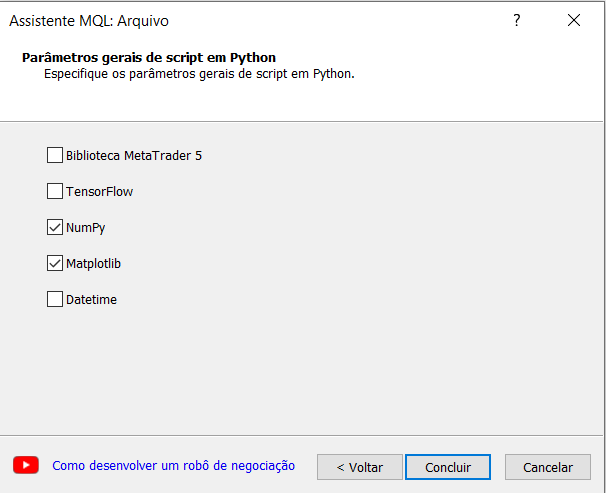
现在，我们创建一个生成正弦图的简单脚本。

# Copyright 2021, Lethan Corp.
# https://www.mql5.com/pt/users/14134597

import numpy as np
import matplotlib.pyplot as plt

data = np.linspace(-np.pi, np.pi, 201)
plt.plot(data, np.sin(data))
plt.xlabel('Angle [rad]')
plt.ylabel('sin(data)')
plt.axis('tight')
plt.show()

为了运行脚本，只需按 F7 进行编译，然后打开 MetaTrader 5 终端，并在图表上运行脚本。 如果有需要打印的内容，则结果将显示在智能系统选项卡中。 在我们的例子中，脚本会打开一个窗口，其中包含我们所创建的函数图。

3 - 正弦图


2. 初期步骤和模型重建（感知器和 MLP）。

 

出于便利起见，我们将采用与 MQL5 示例中相同的数据集合。

下面是 predict() 函数，它针对给定权重集合的指标线预测其输出值。 此处的第一种情况也是偏差。 此外，还有一个激活函数。

# Transfer neuron activation
def activation(activation):
    return 1.0 if activation >= 0.0 else 0.0

# Make a prediction with weights
def predict(row, weights):
    z = weights[0]
    for i in range(len(row) - 1):
        z += weights[i + 1] * row[i]
    return activation(z)

如您所知，为了训练网络，我们需要实现梯度下降过程，这已在上一篇文章中有详细解释。 作为延续，我将展示一个训练函数 “train_weights()”。

# Estimate Perceptron weights using stochastic gradient descent
def train_weights(train, l_rate, n_epoch):
    weights = [0.0 for i in range(len(train[0]))]  #random.random()
    for epoch in range(n_epoch):
        sum_error = 0.0
        for row in train:
            y = predict(row, weights)
            error = row[-1] - y
            sum_error += error**2
            weights[0] = weights[0] + l_rate * error

            for i in range(len(row) - 1):
                weights[i + 1] = weights[i + 1] + l_rate * error * row[i]
        print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))
    return weights


MLP 模型的应用：

本教程分为 5 个部分：

  • 网络启动
  • 前馈
  • 反向传播
  • 训练
  • 预测

网络启动

我们从简单的事情开始，先创建一个新网络，并准备好进行学习。

每个神经元都有一组需要维护的权重，每个输入与一个权重连接，且有一个额外的偏置权重。 我们需要在训练期间保存神经元的其它属性，因此我们将利用字典来表示每个神经元，并按名称存储属性，例如对于权重就是 “weights”。

from random import seed
from random import random

# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
    network = list()
    hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
    network.append(hidden_layer)
    output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
    network.append(output_layer)
    return network

seed(1)
network = initialize_network(2, 1, 2)
for layer in network:
    print(layer)

现在我们知道如何创建和启动网络，我们来看看如何用它来计算输出数据。

    前馈

    from math import exp

# Calculate neuron activation for an input
def activate(weights, inputs):
    activation = weights[-1]
    for i in range(len(weights)-1):
        activation += weights[i] * inputs[i]
    return activation

# Transfer neuron activation
def transfer(activation):
    return 1.0 / (1.0 + exp(-activation))

# Forward propagate input to a network output
def forward_propagate(network, row):
    inputs = row
    for layer in network:
        new_inputs = []
        for neuron in layer:
            activation = activate(neuron['weights'], inputs)
            neuron['output'] = transfer(activation)
            new_inputs.append(neuron['output'])
        inputs = new_inputs
    return inputs

# test forward propagation
network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
        [{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]]
row = [1, 0, None]
output = forward_propagate(network, row)
print(output)

    通过运行上面的脚本，我们得到以下结果：

    [0.6629970129852887, 0.7253160725279748]

    实际输出值现在看来很荒谬。 但我们很快就会看到神经元中的权重如何起更大作用。

    反向传播

    # Calculate the derivative of an neuron output
def transfer_derivative(output):
    return output * (1.0 - output)

# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
    for i in reversed(range(len(network))):
        layer = network[i]
        errors = list()
        if i != len(network)-1:
            for j in range(len(layer)):
                error = 0.0
                for neuron in network[i + 1]:
                    error += (neuron['weights'][j] * neuron['delta'])
                errors.append(error)
        else:
            for j in range(len(layer)):
                neuron = layer[j]
                errors.append(expected[j] - neuron['output'])
        for j in range(len(layer)):
            neuron = layer[j]
            neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])

# test backpropagation of error
network = [[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}],
          [{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095]}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763]}]]
expected = [0, 1]
backward_propagate_error(network, expected)
for layer in network:
    print(layer)

    当运行时，该示例在完成错误检查后打印网络。 如您所见，输出层和隐藏层的误差值已进行计算，并保存在神经元之中。

    [{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614], 'delta': -0.0005348048046610517}]

    [{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095], 'delta': -0.14619064683582808}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763], 'delta': 0.0771723774346327}]

    网络训练

    from math import exp
from random import seed
from random import random

# Initialize a network
def initialize_network(n_inputs, n_hidden, n_outputs):
    network = list()
    hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)]
    network.append(hidden_layer)
    output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)]
    network.append(output_layer)
    return network

# Calculate neuron activation for an input
def activate(weights, inputs):
    activation = weights[-1]
    for i in range(len(weights)-1):
        activation += weights[i] * inputs[i]
    return activation

# Transfer neuron activation
def transfer(activation):
    return 1.0 / (1.0 + exp(-activation))

# Forward propagate input to a network output
def forward_propagate(network, row):
    inputs = row
    for layer in network:
        new_inputs = []
        for neuron in layer:
            activation = activate(neuron['weights'], inputs)
            neuron['output'] = transfer(activation)
            new_inputs.append(neuron['output'])
        inputs = new_inputs
    return inputs

# Calculate the derivative of an neuron output
def transfer_derivative(output):
    return output * (1.0 - output)

# Backpropagate error and store in neurons
def backward_propagate_error(network, expected):
    for i in reversed(range(len(network))):
        layer = network[i]
        errors = list()
        if i != len(network)-1:
            for j in range(len(layer)):
                error = 0.0
                for neuron in network[i + 1]:
                    error += (neuron['weights'][j] * neuron['delta'])
                errors.append(error)
        else:
            for j in range(len(layer)):
                neuron = layer[j]
                errors.append(expected[j] - neuron['output'])
        for j in range(len(layer)):
            neuron = layer[j]
            neuron['delta'] = errors[j] * transfer_derivative(neuron['output'])

# Update network weights with error
def update_weights(network, row, l_rate):
    for i in range(len(network)):
        inputs = row[:-1]
        if i != 0:
            inputs = [neuron['output'] for neuron in network[i - 1]]
        for neuron in network[i]:
            for j in range(len(inputs)):
                neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j]
            neuron['weights'][-1] += l_rate * neuron['delta']

# Train a network for a fixed number of epochs
def train_network(network, train, l_rate, n_epoch, n_outputs):
    for epoch in range(n_epoch):
        sum_error = 0
        for row in train:
            outputs = forward_propagate(network, row)
            expected = [0 for i in range(n_outputs)]
            expected[row[-1]] = 1
            sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))])
            backward_propagate_error(network, expected)
            update_weights(network, row, l_rate)
        print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))

# Test training backprop algorithm
seed(1)
dataset = [[2.7810836,2.550537003,0],
    [1.465489372,2.362125076,0],
    [3.396561688,4.400293529,0],
    [1.38807019,1.850220317,0],
    [3.06407232,3.005305973,0],
    [7.627531214,2.759262235,1],
    [5.332441248,2.088626775,1],
    [6.922596716,1.77106367,1],
    [8.675418651,-0.242068655,1],
    [7.673756466,3.508563011,1]]

n_inputs = len(dataset[0]) - 1
n_outputs = len(set([row[-1] for row in dataset]))
network = initialize_network(n_inputs, 2, n_outputs)
train_network(network, dataset, 0.5, 20, n_outputs)
for layer in network:
    print(layer)

    训练后，打印网络，显示学习到的权重。 此外，网络仍然拥有可以忽略的输出和增量值。 如有必要，我们可以更新我们的训练函数，去删除这些数据。

    >epoch=13, lrate=0.500, error=1.953

    >epoch=14, lrate=0.500, error=1.774

    >epoch=15, lrate=0.500, error=1.614

    >epoch=16, lrate=0.500, error=1.472

    >epoch=17, lrate=0.500, error=1.346

    >epoch=18, lrate=0.500, error=1.233

    >epoch=19, lrate=0.500, error=1.132

    [{'weights': [-1.4688375095432327, 1.850887325439514, 1.0858178629550297], 'output': 0.029980305604426185, 'delta': -0.0059546604162323625}, {'weights': [0.37711098142462157, -0.0625909894552989, 0.2765123702642716], 'output': 0.9456229000211323, 'delta': 0.0026279652850863837}]

    [{'weights': [2.515394649397849, -0.3391927502445985, -0.9671565426390275], 'output': 0.23648794202357587, 'delta': -0.04270059278364587}, {'weights': [-2.5584149848484263, 1.0036422106209202, 0.42383086467582715], 'output': 0.7790535202438367, 'delta': 0.03803132596437354}]

    为了进行预测，我们可用上一个示例中已经配置好的权重集合。

    预测

    from math import exp

# Calculate neuron activation for an input
def activate(weights, inputs):
    activation = weights[-1]
    for i in range(len(weights)-1):
        activation += weights[i] * inputs[i]
    return activation

# Transfer neuron activation
def transfer(activation):
    return 1.0 / (1.0 + exp(-activation))

# Forward propagate input to a network output
def forward_propagate(network, row):
    inputs = row
    for layer in network:
        new_inputs = []
        for neuron in layer:
            activation = activate(neuron['weights'], inputs)
            neuron['output'] = transfer(activation)
            new_inputs.append(neuron['output'])
        inputs = new_inputs
    return inputs

# Make a prediction with a network
def predict(network, row):
    outputs = forward_propagate(network, row)
    return outputs.index(max(outputs))

# Test making predictions with the network
dataset = [[2.7810836,2.550537003,0],
    [1.465489372,2.362125076,0],
    [3.396561688,4.400293529,0],
    [1.38807019,1.850220317,0],
    [3.06407232,3.005305973,0],
    [7.627531214,2.759262235,1],
    [5.332441248,2.088626775,1],
    [6.922596716,1.77106367,1],
    [8.675418651,-0.242068655,1],
    [7.673756466,3.508563011,1]]
network = [[{'weights': [-1.482313569067226, 1.8308790073202204, 1.078381922048799]}, {'weights': [0.23244990332399884, 0.3621998343835864, 0.40289821191094327]}],
    [{'weights': [2.5001872433501404, 0.7887233511355132, -1.1026649757805829]}, {'weights': [-2.429350576245497, 0.8357651039198697, 1.0699217181280656]}]]
for row in dataset:
    prediction = predict(network, row)
    print('Expected=%d, Got=%d' % (row[-1], prediction))

    当示例执行时，它会打印训练数据集合中每条记录的预期结果，随后是网络做出的明确预测。

    根据结果，网络在这个小数据集合上达到了 100% 的准确率。

    Expected=0, Got=0

    Expected=0, Got=0

    Expected=0, Got=0

    Expected=0, Got=0

    Expected=0, Got=0

    Expected=1, Got=1

    Expected=1, Got=1

    Expected=1, Got=1

    Expected=1, Got=1

    Expected=1, Got=1


    3. 利用 Keras 和 TensorFlow 创建一个简单的模型。

    为了收集数据，我们将用到 MetaTrader 5 软件包。 通过导入所需的提取、转换和预测价格的函数库来启动脚本。 我们不会在这里详细研究如何准备数据，然而请不要这对于模型来说是非常重要的一步。

    我们从简要数据概览开始。 数据集合由最后的 1000 跟 EURUSD 柱线组成。 这部分由几个步骤构成：

    • 导入函数库
    • 与 MetaTrader 连接
    • 收集数据
    • 转换数据、调整日期
    • 绘图数据


    import MetaTrader5 as mt5
from pandas import to_datetime, DataFrame
import matplotlib.pyplot as plt

symbol = "EURUSD"

if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

rates = mt5.copy_rates_from_pos(symbol, mt5.TIMEFRAME_D1, 0, 1000)
mt5.shutdown()

rates = DataFrame(rates)
rates['time'] = to_datetime(rates['time'], unit='s')
rates = rates.set_index(['time'])

plt.figure(figsize = (15,10))
plt.plot(rates.close)
plt.show()

    运行代码后，把收盘价数据可视化为下图中的一条线。

    plot_1


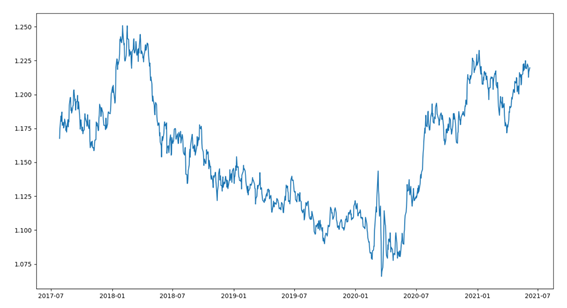
    我们用一个简单的回归方法来预测下一个周期的收盘价。

    对于这个例子，我们将使用单变量方式。

    单变量时间序列是一个数据集合，由含有时间序列的单个观察序列组成。 它需要一个模型，从过去的观察序列中进行学习，以便预测序列中的下一个值。

    第一步是将加载的序列拆分为训练集合和测试集合。 我们来创建一个函数，把这个序列拆分成两部分。 拆分将按照指定的百分比进行，例如 70% 用于训练，30% 用于测试。 对于验证（回测），我们还有其它方法，例如将序列拆分为训练、测试和验证。 鉴于我们在谈论金融序列，我们应该非常小心，避免过度拟合。

    该函数将接收一个 numpy 数组和裁剪值，并将返回两个拆分序列。

    第一个返回值是从位置 0 到 size 的整个集合，代表因子的大小，第二个序列是剩余的集合。

    def train_test_split(values, fator):
    train_size = int(len(values) * fator)
    return values[0:train_size], values[train_size:len(values)]


    Keras 模型可以定义为层的系列。

    我们将创建一个系列模型，并一次添加一层，直到我们对网络架构感到满意为止。

    首先，我们需要确保输入层有正确数量的输入资源。 这可以通过依据参数 input_dim 创建第一层来完成。

    我们怎么知道我们需要多少层和类型？

    这是一个非常难以解答的问题。 我们可以采用启发式，通过反复研判和试错来找到最佳网络结构。 通常，您需要一个足够大的网络来捕获问题的结构。

    在本例中，我们将采用一个全连接的单层网络结构。

    全连接层采用 Dense 类定义。 我们可以指定层中神经元或节点的数量作为第一个参数，并用 activation 参数指定激活函数。

    我们将在第一层采用整流线性单元 (ReLU) 激活函数。

    在预测单变量序列之前，必须先做好准备。

    MLP 模型将调用一个函数来学习，该函数将一系列过去的观察作为输入映射到输出观察中。 因此，必须将观察序列转换为多个示例，模型可以从中进行学习。

    考虑一个单变量序列：

    [10, 20, 30, 40, 50, 60, 70, 80, 90]

    该序列可以拆分为若干个 I/O 形态，称为样本。

    在我们的示例中，我们将在研究预测时采用三个单位步长作为输入，一个单位步长作为输出。

    X,                                          y

    10, 20, 30                          40

    20, 30, 40                          50

    30, 40, 50                          60

    ...

    下面，我们创建了实现此行为的 split_sequence() 函数。 我们还将把单变量集合拆分成若干个样本，每个样本都有一定单位数量的步长。 输出是单个步长。

    我们可以在一小部分数据上测试我们的函数，比如上面例子中的数据。 

    # univariate data preparation
from numpy import array
 
# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
    X, y = list(), list()
    for i in range(len(sequence)):
        # find the end of this pattern
        end_ix = i + n_steps
        # check if we are beyond the sequence
        if end_ix > len(sequence)-1:
            break
        # gather input and output parts of the pattern
        seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
        X.append(seq_x)
        y.append(seq_y)
    return array(X), array(y)
 
# define input sequence
raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90]
# choose a number of time steps
n_steps = 3
# split into samples
X, y = split_sequence(raw_seq, n_steps)
# summarize the data
for i in range(len(X)):
    print(X[i], y[i])

    该代码将单变量集合拆分为六个样本，每个样本含有三个输入单位步长和一个输出单位步长。

    [10 20 30] 40

    [20 30 40] 50

    [30 40 50] 60

    [40 50 60] 70

    [50 60 70] 80

    [60 70 80] 90

    为了继续，我们需要将样本分成 X（特征）和 y（目标），如此我们便可以训练网络。 为此，我们将使用之前创建的 split_sequence() 函数。

    X_train, y_train = split_sequence(train, 3)
X_test, y_test = split_sequence(test, 3)

    现在我们已经准备好了数据样本，我们可以创建 MLP 网络。

    一个简单的 MLP 模型只有一个隐藏的节点层（神经元），和一个用于预测的输出层。

    我们可以定义用于预测单变量时间序列的 MLP，如下所示。

    # define model
model = Sequential()
model.add(Dense(100, activation='relu', input_dim=n_steps))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

    为了定义输入数据的形式，我们需要了解模型期望在单位步长项里为每个样本接收什么样的输入数据。

    作为输入的单位步长是我们为 split_sequence() 函数准备数据集合时选择的数值。

    每个样本的输入维度在第一个隐藏层定义中的 input_dim 参数中指定。 从技术上讲，模型将每个单位步长显示为单独的资源，而不是独个的单位步长。

    通常我们会有多个样本，因此模型期望输入的训练组件具有维度或形状：

    [样本，特征]

    split_sequence() 函数依照准备好的 [样本，特征] 的形式生成 X。

    训练该模型采用名为 Adam 的随机梯度下降高效算法。 它使用 MSE（均方差）损失函数进行优化。

    定义模型后，我们就可以依据数据集合对其进行训练。

    model.fit(X_train, y_train, epochs=100, verbose=2)

    训练模型后，我们可以预测未来的数值。 该模型期望输入形状是二维的[样本，特征]，因此我们需要在进行预测之前重塑单个输入样本。 例如，使用形式 [1, 3] 表示 1 个样本和 3 个单位步长作为特征。

    我们选择测试样本 X_test 的最后一条记录，并在预测后将其与最后一个样本 y_test 中包含的真实值进行比较。

    # demonstrate prediction
x_input = X_test[-1]
x_input = x_input.reshape((1, n_steps))
yhat = model.predict(x_input, verbose=0)

print("Valor previsto: ", yhat)
print("Valor real: ", y_test[-1])


    4. How to integrate MQL5 and Python.

    在交易账户上我们有几个选项可供该模型采用。 其中之一是用本机 Python 函数来开仓和平仓。 但在这种情况下，我们会错过由 MQL 提供的广泛机会。 出于这个原因，我选择了 Python 和 MQL 环境之间的集成，这将令我们在管理仓位/订单方面拥有更多自主权。

    基于 Maxim Dmitrievsky 的文章 MetaTrader 5 和 Python 集成：接收和发送数据，我采用单例范式实现了这个类，它负责创建 Socket 客户端进行通信。 这种范式确保某种类型的对象只有一个副本，因为如果程序里用了两个指针，但均引用自同一个对象，那么这些指针都将指向同一个对象。 

    class CClientSocket
  {
private:
   static CClientSocket*  m_socket;
   int                    m_handler_socket;
   int                    m_port;
   string                 m_host;
   int                    m_time_out;
                     CClientSocket(void);
                    ~CClientSocket(void);
public:
   static bool           DeleteSocket(void);
   bool                  SocketSend(string payload);
   string                SocketReceive(void);
   bool                  IsConnected(void);
   static CClientSocket *Socket(void);
   bool                  Config(string host, int port);
   bool                  Close(void);
  };

    CClienteSocke 类将静态指针存储为私密成员。 该类只有一个构造函数，它是私密的，不能被调用。 替代构造函数代码，我们可以使用 Socket 方法来保证只有一个对象。

    static CClientSocket *CClientSocket::Socket(void)
  {
   if(CheckPointer(m_socket)==POINTER_INVALID)
      m_socket=new CClientSocket();
   return m_socket;
  }

    该方法检查静态指针是否指向 CClienteSocket 套接字。 如果为 true，则返回引用；否则会创建一个新对象，并与该指针相关联，从而确保该对象在我们的系统中是独有的。

    为了与服务器建立连接，需要发起连接。 这里是建立连接的 IsConnected 方法，之后我们就可以开始发送/接收数据了。

    bool CClientSocket::IsConnected(void)
  {
   ResetLastError();
   bool res=true;

   m_handler_socket=SocketCreate();
   if(m_handler_socket==INVALID_HANDLE)
      res=false;

   if(!::SocketConnect(m_handler_socket,m_host,m_port,m_time_out))
      res=false;

   return res;
  }

    在成功连接并传输消息后，我们需要关闭此连接。 为此，我们将调用 Close 方法关闭先前打开的连接。

    bool CClientSocket::Close(void)
  {
   bool res=false;
   if(SocketClose(m_handler_socket))
     {
      res=true;
      m_handler_socket=INVALID_HANDLE;
     }
   return res;
  }

    现在我们需要注册服务器，以后会从它那里接收新 MQL 连接，并向我们的模型发送预测。

    import socket

class socketserver(object):
    def __init__(self, address, port):
        self.sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
        self.address = address
        self.port = port
        self.sock.bind((self.address, self.port))
        
    def socket_receive(self):
        self.sock.listen(1)
        self.conn, self.addr = self.sock.accept()
        self.cummdata = ''

        while True:
            data = self.conn.recv(10000)
            self.cummdata+=data.decode("utf-8")
            if not data:
                self.conn.close()
                break
            return self.cummdata
    
    def socket_send(self, message):
        self.sock.listen(1)
        self.conn, self.addr = self.sock.accept()
        self.conn.send(bytes(message, "utf-8"))
    
            
    def __del__(self):
        self.conn.close()

    我们的对象很简单：在它的构造函数中，我们得到服务器的地址和端口。 socket_received 方法负责接受新连接，并检查是否存在发送的消息。 如果有消息要接收，我们会运行一个循环，直到我们接收完消息的所有部分。 然后关闭与客户端的连接，并退出循环。 另一方面，socket_send 方法负责向我们的客户端发送消息。 因此，这个提议的模型不仅允许我们向我们的模型发送预测，而且还为其它一些事情开辟了可能性 — 这一切都取决于您的创造力和需求。

    现在我们已经准备好进行通信。 我们思考两件事：

    1. 如何训练模型并保存它。
    2. 如何利用经过训练的模型来进行预测。

    若每次我们想要进行预测时，都重新获取数据，并进行训练是不切实际和错误的。 出于这个原因，我总是预先做一些训练，找到最好的超参数，并保存我的模型以备后用。

    我将创建一个名为 model_train 的文件，其中将包含网络训练代码。 我们将使用收盘价之间的百分比差值，并尝试预测这种差值。 请注意，我只想展示如何通过与 MQL 环境集成来使用模型，而不在于模型本身。

    import MetaTrader5 as mt5
from numpy.lib.financial import rate
from pandas import to_datetime, DataFrame
from datetime import datetime, timezone
from matplotlib import pyplot
from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy as np

from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.callbacks import *


symbol = "EURUSD"
date_ini = datetime(2020, 1, 1, tzinfo=timezone.utc)
date_end = datetime(2021, 7, 1, tzinfo=timezone.utc)
period   = mt5.TIMEFRAME_D1

def train_test_split(values, fator):
    train_size = int(len(values) * fator)
    return np.array(values[0:train_size]), np.array(values[train_size:len(values)])

# split a univariate sequence into samples
def split_sequence(sequence, n_steps):
        X, y = list(), list()
        for i in range(len(sequence)):
                end_ix = i + n_steps
                if end_ix > len(sequence)-1:
                        break
                seq_x, seq_y = sequence[i:end_ix], sequence[end_ix]
                X.append(seq_x)
                y.append(seq_y)
        return np.array(X), np.array(y)

if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()
    raise Exception("Error Getting Data")

rates = mt5.copy_rates_range(symbol, period, date_ini, date_end)
mt5.shutdown()
rates = DataFrame(rates)

if rates.empty:
    raise Exception("Error Getting Data")

rates['time'] = to_datetime(rates['time'], unit='s')
rates.set_index(['time'], inplace=True)

rates = rates.close.pct_change(1)
rates = rates.dropna()

X, y = train_test_split(rates, 0.70)
X = X.reshape(X.shape[0])
y = y.reshape(y.shape[0])

train, test = train_test_split(X, 0.7)

n_steps = 60
verbose = 1
epochs  = 50

X_train, y_train = split_sequence(train, n_steps)
X_test, y_test   = split_sequence(test, n_steps)
X_val, y_val     = split_sequence(y, n_steps)

# define model
model = Sequential()
model.add(Dense(200, activation='relu', input_dim=n_steps))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')

history = model.fit(X_train
                   ,y_train  
                   ,epochs=epochs
                   ,verbose=verbose
                   ,validation_data=(X_test, y_test))

model.save(r'C:\YOUR_PATH\MQL5\Experts\YOUR_PATH\model_train_'+symbol+'.h5')

pyplot.title('Loss')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()

history = list()
yhat    = list()

for i in range(0, len(X_val)):
        pred = X_val[i]
        pred = pred.reshape((1, n_steps))
        history.append(y_val[i])
        yhat.append(model.predict(pred).flatten()[0])

pyplot.figure(figsize=(10, 5))
pyplot.plot(history,"*")
pyplot.plot(yhat,"+")
pyplot.plot(history, label='real')
pyplot.plot(yhat, label='prediction')
pyplot.ylabel('Price Close', size=10)
pyplot.xlabel('time', size=10)
pyplot.legend(fontsize=10)

pyplot.show()
rmse = sqrt(mean_squared_error(history, yhat))
mse = mean_squared_error(history, yhat)

print('Test RMSE: %.3f' % rmse)
print('Test MSE: %.3f' % mse)

    我们现在有一个经过训练的模型，它保存在文件夹中，且扩展名为 .h5。 我们能够用这个模型来进行预测。 现在我们来创建一个对象，该对象将此模型实例化，并连接。

    from tensorflow.keras.models import *

class Model(object):
    def __init__(self, n_steps:int, symbol:str, period:int) -> None:
        super().__init__()
        self.n_steps = n_steps
        self.model = load_model(r'C:\YOUR_PATH\MQL5\Experts\YOUR_PATH\model_train_'+symbol+'.h5')

    def predict(self, data):
        return(self.model.predict(data.reshape((1, self.n_steps))).flatten()[0])

    该对象很简单：它的构造函数创建了一个属性的实例，名为 model，该实例将包含保存的模型。 预测模型负责进行预测。

    现在我们需要与客户端交互、接收函数和发送预测的主要方法

    import ast
import pandas as pd
from model import Model
from server_socket import socketserver

host = 'localhost'
port = 9091 
n_steps = 60
TIMEFRAME = 24 | 0x4000
model   = Model(n_steps, "EURUSD", TIMEFRAME)

if __name__ == "__main__":
    serv = socketserver(host, port)

    while True:
        print("<<--Waiting Prices to Predict-->>")
        rates = pd.DataFrame(ast.literal_eval(serv.socket_receive()))
        rates = rates.rates.pct_change(1)
        rates.dropna(inplace=True)
        rates = rates.values.reshape((1, n_steps))
        serv.socket_send(str(model.predict(rates).flatten()[0]))

    在 MQL 客户端，我们需要创建一个机器人来收集数据，并将其发送到我们的服务器，然后从中接收预测。 由于我们的模型是取用已收盘烛条的数据进行训练的，因此我们需要添加一个检查，确保数据只会在烛条收盘后才会收集和发送。 我们应该有完整的数据来预测当前柱线刚刚开盘与已收盘之间的差异。 我们将调用一个函数来检查新柱线的出现。

    bool NewBar(void)
  {
   datetime time[];
   if(CopyTime(Symbol(), Period(), 0, 1, time) < 1)
      return false;
   if(time[0] == m_last_time)
      return false;
   return bool(m_last_time = time[0]);
  }

    m_last_time 变量在全局范围内声明。 它将存储柱线的开盘日期和时间。 如此，我们将检查 'time' 变量是否与 m_last_time 不同：如果为真，则新柱线已开盘。 In this case, the m_last_time should be replaced with 'time'.在这种情况下，应将 m_last_time 替换为新的 “time”。

    如果已有持仓，EA 不应开新仓。 因此，需调用 CheckPosition 方法检查持仓的存在，该方法在全局范围内声明的买入和卖出变量里设置 true 或 false。

    void CheckPosition(void)
  {
   buy = false;
   sell  = false;

   if(PositionSelect(Symbol()))
     {
      if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_BUY&&PositionGetInteger(POSITION_MAGIC) == InpMagicEA)
        {
         buy = true;
         sell  = false;
        }
      if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL&&PositionGetInteger(POSITION_MAGIC) == InpMagicEA)
        {
         sell = true;
         buy = false;
        }
     }
  }

    当一跟新柱线出现时，检查是否有任何持仓。 如果有持仓，则等待平仓。 如果没有持仓，则通过调用 CClienteSocket 类的 IsConnected 方法启动连接过程。

    if(NewBar())
   {
      if(!Socket.IsConnected())
         Print("Error : ", GetLastError(), " Line: ", __LINE__);
    ...
   }

    如果返回 true，则表示我们可以与服务器建立连接，收集数据，并将其发送回。

    string payload = "{'rates':[";
for(int i=InpSteps; i>=0; i--)
   {
      if(i>=1)
         payload += string(iClose(Symbol(), Period(), i))+",";
      else
         payload += string(iClose(Symbol(), Period(), i))+"]}";
   }

    我决定以 {'rates':[1,2,3,4]} 格式发送数据 — 这样我们就可以将它们转换为 Pandas 数据帧，无需在数据转换上浪费时间。

    一旦收集数据完毕，将其发送并等待预测，据此可以制定决策。 我将依据移动平均线来检查价格方向。 根据价格方向和预测值，我们将买入或卖出。

    void OnTick(void)
  {
      ....

      bool send = Socket.SocketSend(payload);
      if(send)
        {
         if(!Socket.IsConnected())
            Print("Error : ", GetLastError(), " Line: ", __LINE__);

         double yhat = StringToDouble(Socket.SocketReceive());

         Print("Value of Prediction: ", yhat);

         if(CopyBuffer(handle, 0, 0, 4, m_fast_ma)==-1)
            Print("Error in CopyBuffer");

         if(m_fast_ma[1]>m_fast_ma[2]&&m_fast_ma[2]>m_fast_ma[3])
           {
            if((iClose(Symbol(), Period(), 2)>iOpen(Symbol(), Period(), 2)&&iClose(Symbol(), Period(), 1)>iOpen(Symbol(), Period(), 1))&&yhat<0)
              {
               m_trade.Sell(mim_vol);
              }
           }

         if(m_fast_ma[1]<m_fast_ma[2]&&m_fast_ma[2]<m_fast_ma[3])
           {
            if((iClose(Symbol(), Period(), 2)<iOpen(Symbol(), Period(), 2)&&iClose(Symbol(), Period(), 1)<iOpen(Symbol(), Period(), 1))&&yhat>0)
              {
               m_trade.Buy(mim_vol);
              }
           }
        }
        
      Socket.Close();
     }
  }

    最后一步是关闭之前建立的连接，等待下一根新柱线的出现。 当新柱线开盘时，开始发送数据和接收预测的过程。

    事实证明，这种架构非常有用，并且具有低延迟。 在一些个人项目中，我在交易账户中采用了这种架构，因为它令我能够享受 MQL 的全部功能，以及 Python 中有关机器学习的大量可用资源。


    下一步是什么？

    在下一篇文章中，我想开发一个更灵活的架构，且能够在策略测试器中使用该模型。

    结束语

    我希望这是一篇关于如何使用和开发各种 Python 模型，以及如何将它们与 MQL 环境集成的有用小教程。

    在本文中，我们：

    1. 搭建 Python 开发环境。
    2. 在 Python 中实现了感知器神经元和 MLP 网络。
    3. 准备用于学习简单网络的单变量数据。 
    4. 设置 Python 和 MQL 之间的通信架构。


    进一步的思路

    本章节提供了一些额外的思路，可以帮助您扩展本教程。

    • 输入尺寸。 探索模型输入的天数，例如 21 天、30 天。
    • 模型优调. 研究各种结构和超参数以获得平均模型性能。
    • 数据伸缩. 了解您是否可以使用数据尺寸（例如标准化和归一化）来提高模型性能。
    • 学习诊断. 使用诸如学习曲线之类的诊断方法来进行学习和验证的误差；使用均方根误差来帮助调整模型的结构和超参数。

    如果您有深入探索这些扩展机会，请分享您的想法。


    本文由MetaQuotes Ltd译自葡萄牙语
    原文地址： https://www.mql5.com/pt/articles/9514

    附加的文件 |
    下载ZIP
    MQL5.zip (179.04 KB)
    注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

    该作者的其他文章

    最近评论 | 前往讨论 (9)
    Hung Wen Lin
    Hung Wen Lin | 17 1月 2022 在 00:38
    Nice
    1441809920
    1441809920 | 27 1月 2022 在 08:20

    after i add the localhost to the url,it still remind me  'error 4014',how to deal with this problem

    the main problem occurs in backtest

    1441809920
    1441809920 | 27 1月 2022 在 18:12
    Hung Wen Lin #:
    Nice
    can you complete the backtest, i found use python  applying the backtest will lead to disconnect
    Ronghua Hu
    Ronghua Hu | 16 2月 2022 在 08:28
    thanks for share,it's a way to create ai for trade
    guicai liu
    guicai liu | 3 4月 2023 在 14:55
    MetaQuotes:

    新文章 多层感知器和反向传播算法（第二部分）：利用 Python 实现并与 MQL5 集成已发布：

    作者：Jonathan Pereira

    MetaQuotes:

    新文章 多层感知器和反向传播算法（第二部分）：利用 Python 实现并与 MQL5 集成已发布：

    作者：Jonathan Pereira

    Does the program developed in this way have to be used on the computer where the machine learning environment is deployed? This program will be very inconvenient to use.

    DoEasy 函数库中的图形（第八十七部分）：图形对象集合 - 在所有打开的图表上管理对象属性修改 DoEasy 函数库中的图形（第八十七部分）：图形对象集合 - 在所有打开的图表上管理对象属性修改
    在本文中，我将继续跟踪标准图形对象事件，并创建允许用户控制在终端中打开的任何图表上放置的图形对象属性更改的功能。
    DoEasy 函数库中的图形（第八十六部分）：图形对象集合 - 管理属性修改 DoEasy 函数库中的图形（第八十六部分）：图形对象集合 - 管理属性修改
    在本文中，我将研究跟踪属性值的修改，以及删除和重命名函数库中的图形对象。
    使用 MQL5.0 社区频道和群聊天 使用 MQL5.0 社区频道和群聊天
    MQL5.com 网站汇集了来自世界各地的交易者。 用户发表文章、共享免费代码、在市场上销售产品、执行自由职业订单、以及跟单信号。 您可以在论坛、交易者聊天和元交易者频道中与他们交流。
    更好的程序员（第 05 部分）：如何成为更迅捷的开发人员 更好的程序员（第 05 部分）：如何成为更迅捷的开发人员
    每位开发人员都希望能够更快地编写代码，且能够更快、更有效地编写代码并非只是少数人与生俱来的特殊能力。 这项技能是可通过学习提升的，这就是我在本文中尝试传授的内容。