
Дискретизация ценового ряда, случайная составляющая и "шумы"
Введение
Классический способ представления ценовых движений в виде временных отрезков возник на заре становления финансовых рынков, когда еще не было компьютеров и вся торговля шла на реальных рынках, реальными товарами. Хранить каждое изменение цены в течении дня было трудно, да и не имело смысла, цены менялись не так быстро. Поэтому представлялось очевидным фиксировать значение цены через определенные промежутки времени. Это логично: "сегодня пшеница стоила 50 рублей, а вчера 49". Все предельно понятно, за сегодня спрос вырос и товар подорожал. Сделок за один день происходило немного по сегодняшним меркам, а значит и переопределение стоимости товара происходило относительно редко.
С развитием анализа ценовых данных, в попытках лучше предсказать поведение цены, и с увеличением числа торговых операций, людям стало важно понимать, какая-же цена была максимальная и минимальная за фиксированный временной отрезок. То есть теперь было недостаточно информации, что вчера цена было 49 рублей, а сегодня 50, необходимо знать, какие максимальные и минимальные значения принимала цена за установленный промежуток времени. Возникла потребность и были придуманы всем известные свечи и бары, которыми мы пользуемся и сегодня.
По мере увеличения числа торговых операций дискретизация ценового ряда становилась все точнее, и сейчас уже актуальна минутная дискретизация, а некоторые применяют и меньшие масштабы, вроде секундной и десятисекундной, все зависит от потребностей.
Основными преимуществами временной дискретизации ценового ряда являются:
- Удобство. Мы точно знаем, что через минуту будет сформирован очередной бар и мы получим новые значения цены открытия, закрытия, максимума и минимума.
- Экономия ресурсов. Представление данных в виде свечей позволяет за промежуток времени хранить только 4 цифры, если не требуется большая точность. Если хранить каждое изменение цены bid, ask, last, то история за год будет иметь значительный объем, исчисляемый гигабайтами, а в некоторых случаях и десятки гигабайт. Если требуется хранить (скачивать) историю не за 1 год, а за 10-20, и еще не по одному инструменту, а по 200-500 инструментам, то это превращается в проблему. К тому же обработка гигабайтов истории для анализа требует значительных вычислительных ресурсов. Поэтому анализ и обработка свечей выглядят более привлекательными.
- Легкое масштабирование и визуальный анализ. Если нужно посмотреть общую картину, мы можем увеличить масштаб дискретизации до недель или даже месяцев и на мониторе будет доступны изменения цен сразу за столько лет, сколько нужно. Но если требуется точность, мы уменьшаем масштаб дискретизации и смотрим, что происходило внутри минуты.
- Линейность во времени. Пожалуй, самое удобное в таком представлении это то, что визуально история за каждый год занимает примерно одинаковое количество места на экране. Легко и интуитивно можно найти на графике прошлый год, прошлый час и так далее. Интуитивно линейность во времени кажется нам очень важным параметром, но бывают случаи, когда "правильные" решения контринтуитивны.
- Простота сравнения цен по разным инструментам в один момент времени.
Особенности дискретизации сигналов
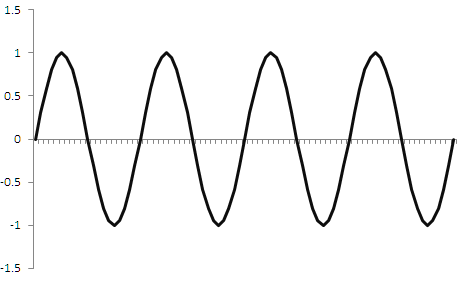
Потребность в дискретизации данных существует не только в трейдинге, но и во многих других областях обработки сигналов. Например, когда вы слушаете музыку, там изначально непрерывный сигнал был оцифрован. Оцифровывается он при помощи дискретизации по времени. То есть через равные промежутки времени берется значение амплитуды сигнала и записывается в память. Затем этот сигнал можно обратно превратить в непрерывный при помощи некоторых манипуляций. И область дискретизации непрерывных сигналов давно и хорошо исследована. В частности, есть такое правило, которое следует из теоремы Котельникова (Найквеста-Шеннона): Сигнал можно полностью восстановить, если частота дискретизации превышает частоту сигнала в 2 и более раз. Это означает, что если у нас частота сигнала 1 герц, то значение его амплитуды нужно считывать минимум 2 раза в секунду (то есть с частотой 2 герца), только тогда после дискретизации можно будет получить его исходную форму. На рисунке 1 ниже показано, что будет, если продискретизировать синусоиду частотой 1 герц, с частотой выборки 2 герца. Зеленым цветом показан сам сигнал, а красным показано, что получается после дискретизации.
Рисунок 1.
После дискретизации из синусоиды получится сигнал треугольной формы. Некоторая ошибка есть, конечно, но при помощи фильтров низкой частоты можно обратно превратить этот треугольный сигнал в синус. То есть восстановить исходный сигнал возможно, да и сам смысл сохраняется, период сохраняется, амплитуда с некоторой погрешностью тоже сохраняется. Если для музыки эти искажения считаются критичными, то для трейдинга нестрашно. Но что получится, если частота дискретизации будет ниже, чем у исходного сигнала? Пример показан на рисунке 2 ниже.
 ---->>
---->> 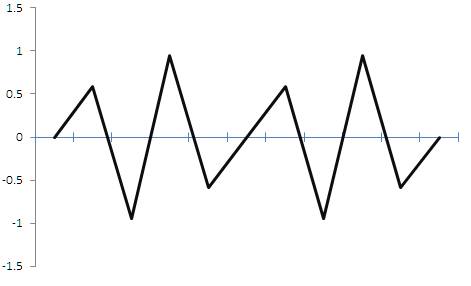
Рисунок 2.
На рисунке видно, что если частота дискретизации меньше, удвоенной частоты сигнала, то сигнал сильно искажается, на выходе и мы получаем, по сути случайный сигнал, не имеющий ничего общего с исходным. Если применительно к трейдингу, то в первом случае мы могли продавать, когда находим максимум и покупать, когда видим минимум. В добавок мы знали периодичность, но после "неправильной" дискретизации у нас потерялась информация как по амплитуде, так и по периодичности сигнала. Так из детерминированного периодического сигнала с известными характеристиками, мы получили случайный непериодический сигнал с неизвестными характеристиками, всего лишь допустив ошибку с выбором частоты дискретизации.
Зная все это, логично должны возникнуть 2 вопроса: "а не допускаем ли мы ошибку при дискретизации ценового ряда?" и "ценовой ряд — это дискретный или непрерывный сигнал и какие у него параметры?"
Ответ не так прост, как может показаться на первый взгляд, но он очень важен.
Ценовой ряд — дискретный или непрерывный?
Ответить на этот вопрос можно, зная механизм формирования рыночной цены. Подробно описывать его не буду, думаю все знают или прочитают в статье "Основы биржевого ценообразования на примере срочной секции Московской биржи". В стакан цен одни участники выставляют заявки и затем другие выкупают нужный объем по нужной цене, так происходит формирования графика цен. Сами уровни получаются дискретные, то есть можно выставить заявку по цене 1, 2, 3 и так далее, с некоторой точностью. Объем, выставляемый в заявках и выкупаемый покупателями, тоже дискретный, потому что можно купить 1,2,3 единицы товара и так далее. На рисунке 3 ниже показан для примера стакан цен, видно, что цены и объемы имеют дискретные значения.
Рисунок 3.
Отсюда можно сделать вывод: сам по себе график ценового ряда имеет дискретную природу. Цена ходит по дискретным уровням после того, как участники выкупают дискретные значения объемов.
Функцией от чего является цена
Мы выяснили, что ценовой ряд сам по себе дискретен, но функцией от какого параметра является изменение цены?
Дискретизировать звуковой сигнал через равные промежутки времени — это приемлемое решение, потому что звуковой сигнал — это функция, меняющаяся от времени. Сам по себе сигнал — это амплитуда, зависящая от времени и это свойство в нем, является фундаментальным. Именно поэтому никаких проблем тут нет.
Природа ценового ряда иная, тут амплитуда (цена) хоть и меняется от времени, но время не является причиной изменения цены. Если задуматься, что-же является причиной изменения цены, то вопрос уже не кажется таким простым. Можно сделать несколько предположений:
- Цена как функция от торговых операций. Тут цена меняется от проведенных торговых операций, поскольку именно торговые операции двигают цену. Но торговые операции могут и не приводить к изменению цены. Например, по цене 5 рублей за акцию доступно 10 акций, участник выкупает 4 акции, остается 6 акций доступно по данной цене, следовательно торговая операция была проведена, а цена не изменилась. При этом данная операция уменьшила объем доступный по данной цене и может стать причиной дальнейшего изменения цены, когда следующий участник выкупи весь объем по данной цене. Цены же меняются только тогда, когда объема доступных по цене 5 рублей за акцию не хватило для удовлетворения спроса и был выкуплен весь объем по цене 5 рублей. В таком случае цена ASK сдвигается на 6 рублей, но все еще остается возможность у других участников выставить еще одну заявку по 5 рублей и вернуть цену ASK на прежнее место.
- Цена как функция от всех операций, проведенных на рынке. Цена может меняться не только от того, что участники выкупают объем по определенному уровню, но и от того, что просто снимают свои заявки и переставляют на другие уровни. Так торговые операции происходить не будут, а цены BID и ASK будут двигаться.
- Цена как функция от "выгоды". Цена может меняться от того, что участники переопределяют для себя стоимость актива, но причины переопределения стоимости актива могут быть совершенно разные. В любом случае переопределение стоимости актива тесно связано с выгодой участников. Теоретически, установившаяся цена будет максимально выгодной для всей совокупности участников, как для покупателей, так и для продавцов (даже если эта выгода отрицательна). Рынок изначально и был создан именно для максимизации выгоды и для определения оптимальной, равновесной цены, устраивающей покупателя и продавца. Причем эта выгода может быть даже не связана с конкретным активом. Например, какому-то инвестиционному фонду срочно требуется выйти из актива, и он готов это сделать даже, получив убытки по этому активу, потому что посчитал, что, совершив такую операцию, он получит какую-то другую выгоду, возможно купив другой актив или даже выплатив прибыль своим клиентам. Природа выгоды тут может быть максимально разнообразной. В таком случае цена и является функцией от каждого переопределения выгоды для каждого участника.
- Цена как функция от самой себя. Очевидно, что каждое изменение цены, точно ведет к изменения выгоды участников торгов. Выгода может меняться и без изменения цены, но когда цена меняется, то выгода участников меняется. Может это не самый точный способ описания ценовых изменений, но он позволяет грубо приблизиться к идеальной модели и сделать ряд допущений, которые в дальнейшем не сильно повлияют на результат. Торгуем мы в основном изменения цены и даже если мы выбираем дивидендные стратегии (совсем не обращая внимания на цену), то в конечном итоге выплата дивидендов приводит к изменению цены. Тут изменение цены и есть сигнал для сдвига графика влево. Фиксируем значение цены, только в те моменты, когда она проходит 1 пункт. Шаг можно сделать любым, зависит от предпочитаемого масштаба, можно фиксировать значение цены, каждый раз, когда она проходит n пунктов по вертикали.
Сам я считаю наиболее вероятным третий вариант, что цена — это функция от переопределения выгоды. Но подсчитывать выгоду каждого участника для дискретизации ценового ряда невозможно. В первых двух случаях реально подсчитывать торговые и неторговые операции на биржевых рынках, но тоже могут возникнуть сложности. Например актив может торговаться на двух и более разных биржах, или ситуация, когда на базовый актив существует производные инструменты, такие как фьючерсы и опционы, нужно ли подсчитывать все операции косвенно связанные с активом или нет, вопрос не простой и заслуживает огромного исследования. В любом случае все четыре случая косвенно связаны между собой, и четвертый вариант, где цена как функция от самой себя, позволяет вести исследования дальше, опираясь на предположение, что это будет грубая модель.
Скорость изменений цены актива точно зависит от количества торговых операций. Чем больше торговых операций, тем чаще будет меняться цена, значит тут существует прямая корреляция. Соответственно, чем больше участников на рынке, тем больше они совершают операций и тем чаще переопределяется выгода для каждого участника, а следовательно, каждый участник будет пытаться чаще переопределить цену, что приведет к большему числу проведенных операций, и тем больше будет частота смены цены на актив.
Особенности дискретизации ценового ряда по временным отрезкам и случайная составляющая
Примем за грубою модель, что цена — это функция от самой себя, то есть дискретизируем цену только тогда, когда она изменяется на определенное количество пунктов. Даже если это не так, то такое допущение позволит дальше раскрыть смысл темы, не сильно повлияв на конечный результат. К тому же для того, чтобы заработать, нам интересно именно то, что цена менялась, а для поиска закономерностей, важно знать, как она менялась.
Каждое изменение цены на 1 пункт (под пунктом понимаем минимально возможное изменение цены) будет представлять собой один шаг и рассмотрим, что происходит, когда мы дискретизируем подобный ряд по времени. Очевидно, что количество пунктов, которое пройдет цена за единицу времени, зависит от торговой активности. Чем выше торговая активность (количество проведенных операций), тем больше шагов в итоге сделает цена. Торговая активность не связана напрямую с движением цены, но так или иначе движение цены зависит от торговой активности и чем выше активность, тем больше будет движений. Связь получается косвенной, но корреляция положительная. Для примера пусть 1 шаг будет 10 пунктов и для примера возьмем часовые свечи. На двух рисунках снизу показано представление цены в виде блоков. Блоки похожи на ренко, но строятся немного по-другому. Из классических свечей взяты значений high и low, которые показывают, какие максимальные и минимальные значения принимала цена, пока формировался блок. Как и у свечей, у блоков есть 4 характеристики: Open High Low Close. Отличие от свечей в том, что расстояние между Open и Close всегда фиксировано и выражено в пунктах. Блок закрывается, когда цена проходит N пунктов по вертикали. Например, размер блока 10 пунктов, тогда как только цена пройдет 10 пунктов по вертикали, блок закрывается и начинается формирование нового блока.
Рисунок 4.
Если принять, что один блок равен одному шагу размером N пунктов, то посмотрим, что происходит внутри часовой свечи. На рисунках 4 показаны движения, которые были за время формирования часовой свечи. Видно, что на верхнем рисунке цена прошла за час 10 блоков по вертикали. Если блоки размером по 10 пунктов, то размер свечи получается 100 пунктов. При этом всего, за время формирования свечи, было сформировано 25 блоков или, по-другому, 25 шагов. На нижнем рисунке показан другой пример, в котором за время формирования свечи, цена прошла 0 блоков по вертикали, а следовательно, 0 пунктов. При этом всего цена прошла 40 блоков или 40 шагов за время формирования цены. Теперь посмотрим на график из таких свечей, представленный ниже на рисунке 5. Свеча закрывается 1 раз в час, а ценовой ряд — это точно не функция от времени, в упрощенном случае это функция от торговых операций, которые, как я писал выше, имеют положительную корреляцию с числом пройденных пунктов. Так как мы превратили пункты в блоки, то число блоков имеет положительную корреляцию с числом торговых операций. Внутри каждой свечи (допустим часовой) оказывается, по сути, случайное число блоков, или шагов по N пунктов, и это будет важно далее. Все потому, что свечи просто закрываются по времени, не обращая внимания на процессы, происходящие на рынке. Время тут получается внешним параметром, который имеет слабое отношение к процессам происходящим с ценой. Другими словами, цена меняется не потому, что прошел час, а по своим причинам, среди которых может быть и то, что прошел час.
Рисунок 5.
Торговая активность может существенно меняться во времени, и у каждого инструмента она индивидуальна. Плюс ко всему, с развитием алготрейдинга, с каждым годом растет и число торговых операций в единицу времени и торговый оборот, а это значит, что сравнивать напрямую часовые свечи за 2010 год и за сегодня будет неправильно, потому что внутри каждой свечи, по сути, разное количество торговых операций.
Далее сделаем еще одно упрощение, примем рынок за случайное блуждание. Естественно, рынок — это неслучайное блуждание, но для понимания так будет проще, потом вернемся обратно к реальным рынкам.
Центральная предельная теорема говорит нам, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному. Применительно к нашему случаю, из центральной предельной теоремы можно получить вывод, что в среднем наш случайный процесс будет проходить за N шагов расстояние пропорционально по вертикали примерно корню квадратному из числа шагов. Если у нас 1 блок это 1 шаг, то за 100 блоков цена в среднем будет проходить 100^0.5 = 10 блоков по вертикали. Где-то больше, где-то меньше, но в среднем наш случайный ценовой ряд будет подчиняться закону нормального распределения. Нужно уточнить, что число шагов у данного случайного ряда будет слабо зависеть от времени, потому что шаги генерирует торговая активность, а она сильно меняется во времени.
Получается, что размер часовой свечи у такого случайного ценового ряда в среднем будет пропорционален числу N^0.5, где N число шагов внутри свечи. То есть размер часовой свечи будет подчинен закону нормального распределения. Далее, принимая во внимание факт, что внутри свечи будет, по сути, случайное число шагов, можно сделать вывод, что и сам размер свечи будет подчинен закону нормального распределения. То есть размер свечи будет равен корню из числа шагов, входящих в эту свечу. Проверим данное утверждение. Для этого буду использовать 50 000 минутных свечей GBPUSD за промежуток 2020.05.18 по 2020.07.03.
- Найдем средний размер минутной свечи по модулю, это будет размер шага. Для этого от цены закрытия каждой следующей свечи отнимем цену закрытия каждой предыдущей свечи и возьмем значение по модулю. У меня получился средний размер минутной свечи GBPUSD = 0,000170
- Найдем средний размер часовой свечи за тот же промежуток (в часовой свече 60 минутных). Для этого от цены закрытия каждой следующей часовой свечи отнимем цену закрытия каждой предыдущей часовой свечи и возьмем значение по модулю. У меня получился средний размер часовой свечи GBPUSD = 0,001117
- Найдем, сколько должна в среднем проходить цена за час, если допустить, что ценовой ряд — это случайное блуждание. Для этого средний размер минутной свечи умножим на корень из числа шагов, и умножим на средний размер шага. У нас число шагов 60 => 0,000170*(60^0.5) = 0.001315. К такому среднему размеру стремился бы размер часовой свечи был бы, если бы исходный ряд подчинялся закону нормального распределения.
- Сравним средний размер реальной свечи и свечи случайного блуждания (реальный 0,001117) ≈ (0.001315 теоретический). Отличие всего 0,0002. Можно сделать вывод, что допущение о том, что размер свечи подчинен закону нормального распределения не просто верно, но и подтверждается рыночными данными реального инструмента. Отличие в 0,0002 несущественно.
Далее, используя полученные часовые свечи, мы, по сути, объединяем и анализируем последовательность неких отрезков ценового ряда, амплитуда которых подчиняется закону нормального распределения. И ничего удивительного, если дальше, переходя на высшие таймфреймы, мы получаем все те же свечи, размер которых пропорционален корню из числа шагов. Так мы возвращаемся к тому, что изображено на рисунке 2, а именно — при неправильной дискретизации какого-то ряда на выходе мы получаем случайную последовательность. По сути, при помощи дискретизации по времени мы превращаем ценовой ряд в случайную последовательность. Да, закономерности все еще могут оставаться и на последовательностях с временной дискретизацией, по тому, что рынок не случайная последовательность и косвенные зависимости от времени тут присутствуют, но анализ такого ряда и выявление закономерностей, становится намного сложнее. Именно из-за временной дискретизации на ценовом ряде появляются так называемые "шумы" и нестационарности, о которых многие говорят, но не говорят, что это за шумы и откуда они берутся. Теперь под шумами можно понимать не только шумы дискретизации, которые возникают во время дискретизации сигнала, но и случайную составляющую, которая возникает из-за неправильных параметров дискретизации ценового ряда, который сам по себе уже является дискретным.
Для того, чтобы убедиться, что полученные результаты с часовыми свечами не были случайным совпадением, проведем подобную операцию для дневных свечей. В сутках 24 часа, так как валютные пары торгуются круглосуточно, то можно сказать, что в дневной свече содержится 1440 минутных свечи. Нарежем тот же интервал минутных данных, которые использовали для построения H1. Только в этот раз, для удобства, все данные выведу в виде таблицы.
| Средний размер свечи m1 | Средний реальный размер свечи H1 | Теоретический размер свечи H1, рассчитанный как 0.000117*(60^0.5) | Средний реальный размер свечи D1 | Теоретический размер свечи D1, рассчитанный как 0.00017*(1440^0.5) |
|---|---|---|---|---|
| 0.000170 | 0.001117 | 0.001315 | 0.006547 | 0.006442 |
Как видно, реальный средний размер дневной свечи не сильно отличается от того размера, который предсказывается теоретически, если бы это был не реальный рынок, а случайное блуждание. Файл с историческими данными и расчетами я приложу к статье в формате Excel.
До этого для расчета среднего размера свечи старшего таймфрейма использовались данные минутного таймфрейма. Но что, если спуститься ниже и использовать тиковые данные, может тогда получатся другие результаты? Для этого:
- Возьмем данные по тиковому объему минутных свечей (с реального счета) за тот же период и найдем среднее число тиков в минутной свече, получилось в среднем значение 59.99 тика в минуту.
- Теперь загрузим тиковые данные и узнаем средний размер тика, он получается 0,000014378.
- Посчитаем теоретический размер минутой свечи, как (59,99^0.5)*0.00014378=0.000111363
- Посчитаем теоретический размер часовой свечи, как ((59,99*60)^0.5)* 0.000014378= 0.00086
| Средний размер тика | Средний реальный размер свечи m1 | Теоретический размер свечи m1, рассчитанный как (59,99^0.5)*0.000014378 | Средний реальный размер свечи H1 | Теоретический размер свечи H1, рассчитанный как ((59,99*60)^0.5)* 0.000014378 |
|---|---|---|---|---|
| 0.000014378 | 0.00017 | 0.000111363 | 0.001117 | 0.00086 |
Как видно, средний размер свечи m1 и H1, не сильно отличается от теоретического, который имел бы ценовой ряд, если бы был случайным блужданием, откуда можно сделать вывод, что по какой-то причине ценовой ряд похож по своему поведению на случайное блуждание и, возможно , это связано с неправильной дискретизацией временными отрезками.
Плотность распределения приращений ценового ряда
Количественная оценка позволила грубо оценить, насколько размер свечей ценового ряда соответствует размеру свечей случайного блуждания, но интереснее построить плотность распределений приращений ценового ряд, чтобы оценить визуально сходства или отличия с плотностью распределения приращений для случайного блуждания.
Подготовка данных для анализа занимает немаловажную часть. Плотность распределения будем строить для количества пунктов, которое цена может пройти за 60 минут (за час), то есть за 60 шагов. Для этого нужно знать средний размер минутной свечи и число шагов (сколько минутных свечей в часовой свече). Средний размер минутной свечи мы вычисляли ранее, и он равен 0.000170, число минутных свечей в часовой 60. Значит, за час цена может сделать 60 шагов по 0,000170. Следовательно, крайние случаи будут, когда цена от начальной точки пройдет непрерывно 60 шагов вверх или 60 шагов вниз. Поэтому оценивать плотность распределения будем в диапазоне -0,00017*60=-0,0102 до 0,00017*60=0,0102. Другими словами, мы знаем, что если цена будет идти только вверх, шагами 0,00017, то за 60 шагов (за час) максимум она дойдет до значения 0,0102. Причем для 60 шагов, цена сможет занимать только дискретные уровни 0; 0.00034; 0,00068; 0,00102...0,0102 и аналогичные отрицательные значения. Проиллюстрировать почему именно цена будет занимать эти уровни можно при помощи рисунка 6.
Рисунок 6.
На рисунке 6 видно, что если какая-то дискретная функция выходит из нулевой точки, ее шаг равен 1 и всего она делает 6 шагов, то в конечном итоге она может пройти по вертикали 6; 4; 2; 0, делений, она может принимать только дискретные значения с интервалом двойного шага. Аналогично и для нашего случая, если средний размер минутной свечи 0,00017, то цена может занимать дискретные уровни с интервалом равным удвоенному размеру свечи. В реальности, так как свечи бывают разного размера, не только 0,00017, цена может принимать промежуточные значения, поэтому для анализа мы будем подсчитывать, сколько событий попадает в интервалы с двойным средний размером свечи. Для того, чтобы сравнить, насколько сильно отличается полученное распределение для ценового ряда, мы сравним его с распределением для случайного блуждания. Для случайного блуждания характерно то, что вероятность смены направления каждого следующего шага равна 50% и отсутствует память. На рисунке 7, показаны распределения плотности вероятностей черным цветом для ценового ряда, красным цветом для случайного блуждания.
Рисунок 7.
Из рисунка 7, видно, что плотность распределения вероятностей ценового ряда почти совпадает с плотностью распределение вероятностей для случайного блуждания. Плотность распределения вероятностей ценового ряда имеет чуть более высокий пик, чуть уже и немного смещена вправо, относительно плотности распределения для случайного блуждания. Это говорит о том, что вероятность разворота каждого следующего шага у ценового ряда чуть выше 50%, и присутствует небольшой восходящий тренд, но эти отличия не велики. Сразу возникает соблазн заработать на этом отклонении, казалось бы, сделать это несложно, но в следующей статье мы подробно рассмотрим эту закономерность и возможность заработка на ней. Тут нужно понимать, что идет речь об идеальной случайной величине, которая при достаточно большой выборке будет стремиться к эталону. График плотности распределения вероятности для случайного блуждания построен при помощи таблицы, часть которой показана на рисунке 8.
Рисунок 8.
Построенный график распределения плотностей вероятности подтверждает выводы, сделанные ранее о том, что размер свечей (в данном случае часовых) стремится к такому размеру свечей, который был бы, если бы ценовой ряд являлся случайным блужданием, но позволяет оценить этот факт визуально и более точно.
Все данные и расчеты, которыми я оперирую в статье, прикреплены к статье в формате xlsx, в этом файле можно будет найти все расчеты.
Участки высокой и низкой волатильности
Внимательный трейдер может возразить, что на графиках часто даже визуально можно увидеть, как на рынке свечи условно поделены на группы "больших" и "маленьких" размеров (участки с высокой и низкой волатильностью), значит график не случайное блуждание и закономерности есть. Если бы временная дискретизация вносила такие сильные искажения, то такого эффекта не наблюдалось. Но этот факт как раз и объясняется тем, что размер свечей зависит от числа торговых операций, проведенных внутри этой свечи. Как это можно проверить? Достаточно посмотреть на график, на котором нанесены тиковые объемы и видно, что периоды с "маленькими свечами" сопровождаются периодами с низкими тиковыми объемами, а периоды с большими свечами, сопровождаются периодами больших тиковых объемов. Если представить, что один тик — это один шаг, то в периоды "больших" свечей цена делает больше шагов и, соответственно, имеет больший размер, но сам размер свечи остается пропорционален квадратному корню из числа шагов, умноженному на средний размер шага (пример на рисунке 9). Тиковые объемы в свою очередь имеют прямую корреляцию с торговой активностью, чем выше торговая активность, тем больше проходит тиков в единицу времени. На биржевых рынках доступна история реальных объемов и там можно наблюдать, что размер тиковых объемов сильно коррелирует с реальными объемами, что так же говорит о связи числа тиков с интенсивностью торговли.
Рисунок 9.
Этот факт еще раз доказывает, что дискретизация временными отрезками вносит сильные искажения в итоговую форму ценового ряда и существенно затрудняет анализ. Подобное искажение привело к появлению целого класса торговых систем, так называемых "ночных скальперов". Я не утверждаю, что они неспособны приносить прибыль, но во время разработки подобного рода систем нужно учитывать данную особенность представления ценового ряда и проводить дополнительные исследования, которые должны ответить на вопрос: "действительно ли на данных участках вероятность разворота выше, чем вероятность продолжения тенденции" и "позволяют ли статистические характеристики данных участков извлечь прибыль", потому что именно эту закономерность и эксплуатируют системы подобного рода.
Альтернативный вариант дискретизации ценового ряда
После анализа напрашивается простой вывод, что лучше всего использовать для обработки и анализа тиковые данные, чтобы не вносить свои ошибки дискретизации в исходный ценовой ряд, потому что цена и так приходит дискретной. Если потребуется увеличить масштаб, то просто будем делать блоки по 10 тиков или 100. Но проблема в том, что сами тики — это тоже способ дискретизации. Да, этот способ устоявшийся и широко используемый, но он может вносить искажения в процесс, ведь цена не является функцией от пришедших тиков. Цена как минимум является функцией от проведенных торговых операций, а торговая операция может и не генерировать тик. На бирже тики хоть как-то связаны с реальной торговлей, а на FOREX каждая компания может транслировать сколько угодно тиков, и у кого они "правильные" выяснить не получится. Поэтому даже при таком простом допущении, что цена является функцией от торговых операций, становится понятно, что тики уже искажают форму ценового ряда и вносят случайную составляющую, которая при дальнейшем анализе может приводить к ошибкам.
Вопрос "правильной" дискретизации занимает немаловажную часть анализа данных. Например, на рисунке 10 ниже показаны 2 графики цены биткоина к доллару. Верхний график — это обычный график, построенный из недельных свечей, а нижний график продискретизирован блоками по N пунктов. Это один и тот же период, одинаковое число блоков/свечей, но разные способы дискретизации. Видно, как сильно отличаются графики на один и тот же актив. Поэтому возникает закономерный вопрос: "а какое из двух отображений правильное?"
Рисунок 10.
Я пришел к выводу, что правильное отображение то, которая учитывает природу дискретности ценового ряда. Но так как природа дискретности остается неизвестна, то "правильнее" будет использовать тот способ дискретизации, который способен отразить получение прибыли/убытка как мной, так и остальными участниками рынка. Соответственно анализировать предпочтительнее те данные, на основании которых и формируется наш заработок. То есть не рассматривать движение цены во времени, а учитывать только то, на сколько сдвинулась цена.
Альтернативой временной дискретизации может быть дискретизация с фиксированной амплитудой, где делается допущение, что цена — это функция от самой себя. То есть те блоки, о которых я писал выше. Мы считаем, что закрылся блок размером N пунктов, каждый раз, когда цена проходит N пунктов по вертикали. Возможно, это не самый лучший подход, но во время торговли нас, как и многих других участников, интересует именно то, сколько цена прошла пунктов, потому что именно от этого зависит то, сколько мы получим прибыли или убытка. К тому же именно после того, как цена прошла N пунктов по вертикали, меняется выгода каждого участника. То есть модель, при которой цена является функцией от самой себя, наиболее близка к реальной торговле. На рисунке 11 показано, как была продискретизирована синусоида блоками фиксированного размера. При этом потерялась форма, но основные важные для нас характеристики, такие как период и амплитуда, сохранились.
Рисунок 11.
Даже если мы ошибемся с параметрами дискретизации, ничего страшного не произойдет, значения амплитуды и периода будут сохраняться. На рисунке 12 ниже показан пример, что происходит, когда размер блока слишком большой. Теряется часть информации, которая находится внутри блока, то есть ухудшается точность и теряется часть информации (что неизбежно при сжатии данных), но при этом сохраняется информация по амплитуде и периоду. Если же размер блока будет больше, чем амплитуда ценового ряда, то блоки не будут отображаться. Как видно, в отличии от примера, показанного на рисунке 2, при неправильном выборе параметра дискретизации исходный детерминированный сигнал не превращается в случайный сигнал.
Рисунок 12
Таким способом можно бороться со случайной составляющей, которую вносит дискретизация ценового ряда по времени и в ситуациях, когда неизвестно, функцией от какого параметра является исходный ряд. Данный метод работает лучше, чем дискретизация по времени и позволяет удобно масштабировать график с точностью изменения масштаба до 1 пункта.
Заключение
- Природа ценового ряда дискретна, что следует из самой структуры ценообразования.
- Рыночная цена не является функцией от времени, это функция от тесно связанных между собой экономический процессов и учесть их все на данный момент не представляется возможным.
- Дискретизация ценового ряда временными отрезками вносит существенную случайную составляющую, искажая реальную форму графика цены, добавляя "шумы" и нестационарность к без того сложному процессу с неизвестными параметрами.
- При разработке методов дискретизации ценового ряда, нужно учитывать функцией от какого параметра является цена.
- Нестационарность ценового ряда образуется, в том числе, из-за неправильных параметров дискретизации.
- Анализировать графики цены с временной дискретизацией на наличие закономерностей можно, но вышеперечисленные аспекты нужно учитывать, чтобы лучше понимать природу той или иной найденной закономерности.
- Нужно разрабатывать способы дискретизации ценового ряда, вносящие намного меньше искажений в исходные данные, один из них представлен в этой статье.
- При разработке торговых алгоритмов и статистических исследованиях рынка нужно учитывать особенности используемой дискретизации ценового ряда.
 Что такое тренды и какова структура рынков — трендовая или флэтовая?
Что такое тренды и какова структура рынков — трендовая или флэтовая?
 Использование криптографии совместно с внешними приложениями
Использование криптографии совместно с внешними приложениями
 Система голосовых уведомлений торговых событий и сигналов
Система голосовых уведомлений торговых событий и сигналов
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
На рисунке 7, показаны распределения плотности вероятностей черным цветом для ценового ряда, красным цветом для случайного блуждания.
Рисунок 7.
Из рисунка 7, видно, что плотность распределения вероятностей ценового ряда почти совпадает с плотностью распределение вероятностей для случайного блуждания. Плотность распределения вероятностей ценового ряда имеет чуть более высокий пик, чуть уже и немного смещена вправо, относительно плотности распределения для случайного блуждания. Это говорит о том, что вероятность разворота каждого следующего шага у ценового ряда чуть выше 50%, и присутствует небольшой восходящий тренд, но эти отличия не велики.
Скорее всего, причина выделенного - что стат. исследование делалось в пунктах.
Скорее всего, причина выделенного - что стат. исследование делалось в пунктах.
А в каких единицах было бы интереснее делать?
А в каких единицах было бы интереснее делать?
Логичнее в относительных величинах смотреть. Поэтому целесообразно логарифмировать цВР перед стат. исследованиями с returns.
Логичнее в относительных величинах смотреть. Поэтому целесообразно логарифмировать цВР перед стат. исследованиями с returns.
У Вас же не возникал этот вопрос, когда брали разность цен. Здесь - аналогично.