
Прогнозирование временных рядов (Часть 2): метод наименьших квадратов опорных векторов (LS-SVM)
Ключевые слова: LS-SVM, SOM-LS-SVM, SOM
Введение
В данной статье мы продолжим рассказ об алгоритмах прогнозирования временных рядов. В первой части был освещен метод прогнозирующей эмпирической модовой декомпозиции (EMD) и индикатор TSA для статистического анализа временных рядов. В этой второй части объектом исследования станет алгоритм опорных векторов (support-vector machine, SVM) в его модификации наименьших квадратов (Least-squares support-vector machine, LS-SVM). Данная технология до сих пор не была ещё реализована на MQL. Но сначала нам потребуется познакомиться с некоторым математическим аппаратом.
Математический аппарат LS-SVM
Метод опорных векторов (Support Vector Machine, SVM) — это обобщающее название для группы алгоритмов анализа данных, используемых для классификации и регрессии. Для нас особый интерес представляет именно регрессия (статья в английской Wikipedia), потому что она выявляет взаимосвязь между зависимыми и независимыми переменными (предикторами). Задачу прогнозирования можно сформулировать через регрессию как нахождение некой функции, зависящей от прошлых отсчетов временного ряда (тех самых предикторов), такой, что её значения максимально правдоподобно описывают будущие отсчеты ряда.
В основе алгоритма SVM лежит перевод исходных данных в пространство более высокой размерности, где каждый входной вектор формируется как последовательность исходных точек с временными задержками. Далее эти вектора используются в качестве опорных образцов, из комбинации которых особым образом вычисляется регрессионная гиперплоскость, описывающая распределение данных с заданной точностью. Вычисления представляют собой суммирование по всем образцам так называемых ядер (kernels) — единообразных функций от входных данных. Эти функции могут быть линейными или нелинейными (обычно колоколообразными), и управляться параметрами, влияющими на точность регрессии. К числу наиболее распространенных ядер относятся:
- линейное
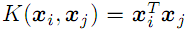 ;
; - полиномиальное степени d
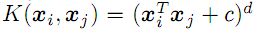 ;
; - радиальная базисная функция с дисперсией "сигма" (Гауссиан, см. ниже);
- сигмоида (гиперболический тангенс)
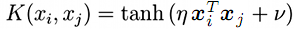 ;
;
Существует модификация SVM — Least-Squares SVM (LS-SVM) или дословно в переводе на русский — метод наименьших квадратов опорных векторов. Он позволяет вместо исходной нелинейной задачи решить эквивалентную в виде системы линейных уравнений.
Допустим, у нас есть временной ряд y и мы предполагаем, что можем узнать его значение в момент t как функцию от p предыдущих точек и некоторых внешних q переменных, с ошибкой e. В общем виде это запишется так:
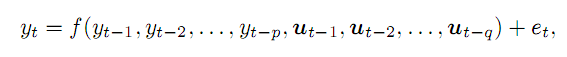 (1)
(1)
В качестве примеров внешних переменных (для прикладной области трейдинга) можно привести номер дня недели, номер часа в сутках, или объем соответствующего бара. В данной статье мы ограничимся лишь предыдущими точками временного ряда цен. Сложность материала не позволяет рассмотреть сразу все аспекты.
Взятые из ряда p предыдущих точек формируют вектор в p-мерном пространстве. Продвигаясь по исходному ряду слева направо мы получим набор векторов-предикторов, которые обозначим x, и для момента времени t их соответствие прогнозу y выражается так:
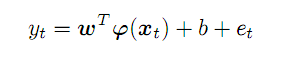 (2)
(2)
Неизвестный вектор коэффициентов w и трансформирующие функции f работают в абстрактном пространстве признаков, размерность которого потенциально ничем не ограничена и может быть даже выше, чем p, а вид f, как и значения коэффициентов w как раз и требуется найти в процессе оптимизации:
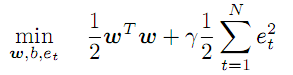 (3)
(3)
Данное условие предписывает минимизировать величину коэффициентов w и вводит регуляризующий (штрафной) коэффициент "гамма" для величины ошибок. Чем больше "гамма", тем точнее регрессия должна приближать исходные данные. Если "гамма" уменьшается, допуск отклонений увеличивается и тем самым повышается гладкость модели.
Ограничениями выступает система уравнений (2) для всех t от 1 до N (количество векторов).
Чтобы упростить задачу применяют математические "трюки" (один из них так и называется — kernel trick): вместо исходной оптимизационной задачи решают так называемую дуальную, по сути эквивалентную, в которой удается избавиться от коэффициентов w и трансформаций f в обмен на ядерные функции (см. далее). В результате решение сводится к линейной системе:
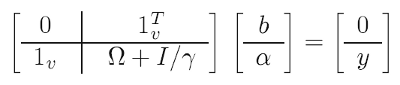 (4)
(4)
Известные данные в ней:
- y - вектор, состоящий из всех целевых (обучающих) значений прогноза;
- 1 - единичные вектора (строка и столбец);
- I - единичная матрица;
- гамма - описанный выше регуляризующий параметр (его нужно подбирать, руководствуясь качеством прогноза на тестовой выборке);
- омега - матрица, рассчитываемая по формуле:
![]() (5)
(5)
И здесь мы наконец встречаем анонсированные ранее ядерные функции K, рассчитываемые на попарных комбинациях между всеми входными векторами x. Для радиальной базисной функции в виде симметричного Гауссиана (мы будем использовать именно её) формула K выглядит следующим образом:
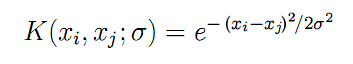 (6)
(6)
Параметр "сигма" описывает ширину колокола — это еще один параметр, который нужно подбирать итеративно на практике. Чем больше "сигма", тем большее количество "окрестных" векторов будет принимать участие в регрессии. Когда "сигма" мала, функция фактически точно проходит по точкам обучающего набора данных и перестает реагировать на неизвестные образы (обобщать).
С помощью исходных данных (x, y), по формулам (4), (5) и (6) мы методом наименьших квадратов получаем все неизвестные:
- b - свободный член, фигурирующий в (2) и (7);
- a - вектор коэффициентов "альфа", которые входят в окончательную формулу регрессионной модели:
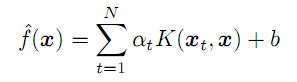 (7)
(7)
Для любого произвольного вектора x (не из обучающего множества), она позволяет вычислить прогноз как сумму произведений коэффицентов "альфа" и ядер по всем исходным N векторам, с поправкой на свободный член b.
В теоретической части остается ответить на 2 вопроса. Во-первых, каким образом мы узнаем свободные параметры "гамма" и "сигма". Во-вторых, какую следует выбирать глубину временных задержек p для формирования входных векторов x из ряда котировок.
Параметры определяются фактически методом "проб и ошибок": в цикле по очень широкой двумерной сетке значений делается расчет модели для каждого сочетания и определяется её качество. Под качеством будем понимать минимизацию ошибки прогнозирования на тестовом наборе данных, отличном от набора обучения. Процесс напоминает и может задействовать оптимизацию в тестере MetaTrader, но для исследования широких диапазонов потребуется фактически менять значения не с постоянным шагом, а в геометрической прогрессии — с помощью умножения. Поэтому нам потребуется учесть данную особенность на стадии реализации.
Что касается размера входного пространства p, его рекомендуется определять исходя из характеристик прогнозируемого ряда, в частности, с помощью частной автокорреляционной функции (PACF). В предыдущей статье мы подготовили инструментарий для расчета PACF и видели, как она выглядит на дифференцированном EURUSD D1 для конкретного участка истории. Каждый столбик гистограммы описывает влияние баров с соответствующим временным лагом на текущий бар (то есть, в целом по всей выборке, попарно между барами с индексами, отличающимися на величину лага). 2 пунктирные кривые линии сверху и снизу обозначают границы 95%-ого доверительного интервала. Большая часть отсчетов PACF лежит внутри интервала, но некоторые выходят за его пределы. Строго говоря, при формировании входных векторов имеет смысл в первую очередь брать отсчеты с большими значениями, так как они указывают на связь нового бара и соответствующих прошлых баров. Иными словами, в вектор y можно было бы складывать не все прошлые отсчеты подряд, а, например, 6-ой, 8-ой и 50-й, как на картинке из прошлой статьи. Однако, данная ситуация характерна только для конкретной выборки. Если мы возьмем, не 500 баров D1, а 1000 или 250, получим новую PACF с другими "всплесками". Таким образом, "прореживание" отсчетов исходного ряда потребуется делать при любом изменении данных, а это в свою очередь потребует переоптимизации настроек LS-SVM (в частности, параметров "гамма" и "сигма"). Поэтому, в целях повышения универсальности алгоритма, хоть и за счет некоторой потери эффективности, было решено формировать входные вектора из всех последовательных баров на заданную глубину p, чтобы на этом начальном участке PACF происходило покрытие доверительным интервалом основных "выбросов". На практике это означает p в диапазоне от 20 до 50 баров для EURUSD D1.
Наконец, стоит отметить, что вычислительная сложность LS-SVM квадратично зависит от длины выборки N, поскольку размер матрицы равен (N+1)*(N+1). Для выборок в несколько сотен и тысяч баров это может негативно сказаться на производительности. Существует много разновидностей LS-SVM, которые пытаются бороться с этим "проклятием размерности". Один из них, например, предполагает сперва кластеризовать все вектора с помощью нейронной сети Кохонена (SOM), а затем проводить обучение отдельных M моделей для каждого кластера (M - число кластеров).
Я предлагаю иной подход. После кластеризации исходного набора векторов сетью SOM, найденные кластеры будут использоваться в качестве ядер вместо исходных векторов. Например, выборка из 1000 векторов может быть отображена на слой Кохонена размером 7*7, т.е. 49 опорных векторов, что в среднем дает примерно по 20 исходных образцов на каждую ячейку сети.
Сеть Кохонена уже была рассмотрена в статьях Практическое использование нейросетей Кохонена в алгоритмическом трейдинге (Часть I, Часть II), поэтому её сравнительно просто встроить в создаваемый движок LS-SVM.
Приступим к реализации алгоритма на MQL.
LS-SVM на MQL
Все расчеты сведем в один класс LSSVM, который будет использовать линейные "решатели" библиотеки ALGLIB. Поэтому подключим её в исходный код, и библиотеку CSOM за одно.
#include <Math/Alglib/dataanalysis.mqh> #include <CSOM/CSOM.mqh>
В классе обеспечим хранение всех входных векторов и матриц LS-SVM:
class LSSVM { protected: double X[]; double Y[]; double Alpha[]; double Omega[]; double Beta; double Sigma; double Sigma22; // 2 * Sigma * Sigma; double Gamma; int VectorNumber; int VectorSize; int Offset; int DifferencingOrder; ...
Класс будет сам заполнять X и Y данными из котировок, руководствуясь запрошенным количеством векторов VectorNumber, их размером VectorSize, и смещением на истории Offset (по умолчанию, 0 — самые последние цены), всё это передается через параметры в конструктор.
Класс поддерживает обработку не только исходного ряда (DifferencingOrder равно 0), но и его разниц порядков от 1 до 3. Нюансы этого приема будут далее рассмотрены более подробно.
Опциональную кластеризацию с помощью сети Кохонена обеспечивает объект KohonenMap, а найденные им кластеры попадают в массив Kernels.
double Kernels[]; // SOM clusters int KernelNumber; CSOM KohonenMap; ...
Размер сети (предполагается квадратный слой, т.е. число KernelNumber должно быть квадратом целого) задает пользователь, и этот параметр тоже можно оптимизировать. Если KernelNumber равно 0 (по умолчанию) или общему числу векторов, SOM отключается и в ход вступает стандартная обработка с помощью LS-SVM. Работа с сетью выходит за рамки статьи, желающие могут ознакомиться с методами её подготовки, обучения и интеграции в прилагаемых исходных кодах. Учтите, что сеть изначально рандомизуется, и потому для получения воспроизводимых результатов нужно вызывать srand с конкретным значением.
Данные по умолчанию считываются из таймсерии цен открытия в методе buildXYVectors. В данной статье мы будем работать только с ними. Для ввода произвольных данных предусмотрен метод feedXYVectors, но он не тестировался.
bool buildXYVectors() { ArrayResize(X, VectorNumber * VectorSize); ArrayResize(Y, VectorNumber); double open[]; int k = 0; const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y CopyOpen(_Symbol, _Period, Offset, size, open); double diff[]; ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction for(int i = 0; i < VectorNumber; i++) // loop through anchor bars { for(int j = 0; j < VectorSize; j++) // loop through successive bars { differentiate(open, i + j, diff); X[k++] = diff[0]; } differentiate(open, i + VectorSize, diff); Y[i] = diff[0]; } return true; }
Вызываемый здесь вспомогательный метод differentiate позволяет посчитать для переданного массива разницу произвольного порядка — результат возвращается через массив diff, длина которого на 1 больше DifferencingOrder.
void differentiate(const double &open[], const int ij, double &diff[]) { for(int q = 0; q <= DifferencingOrder; q++) { diff[q] = open[ij + q]; } int d = DifferencingOrder; while(d > 0) { for(int q = 0; q < d; q++) { diff[q] = diff[q + 1] - diff[q]; } d--; } }
Класс поддерживает нормализацию векторов с помощью вычитания среднего и деления на стандартное отклонение в методе normalizeXYVectors (здесь не приводится).
В классе также имеется пара методов расчета ядер — как для векторов из X[] по их индексам, так и для внешних векторов, например:
double kernel(const double &x1[], const double &x2[]) const { double sum = 0; for(int i = 0; i < VectorSize; i++) { sum += (x1[i] - x2[i]) * (x1[i] - x2[i]); } return exp(-1 * sum / Sigma22); }
Расчет матрицы "омега" выполняет метод buildOmega (он использует метод kernel с обращением к векторам X[] по индексам):
void buildOmega() { KernelNumber = VectorNumber; ArrayResize(Omega, VectorNumber * VectorNumber); for(int i = 0; i < VectorNumber; i++) { for(int j = i; j < VectorNumber; j++) { const double k = kernel(i, j); Omega[i * VectorNumber + j] = k; Omega[j * VectorNumber + i] = k; if(i == j) { Omega[i * VectorNumber + j] += 1 / Gamma; Omega[j * VectorNumber + i] += 1 / Gamma; } } } }
Непосредственно решение системы уравнений и получение искомых коэффициентов "альфа" и "бета" происходит в методе solveSoLE.
bool solveSoLE() { // | 0 |1| | | Beta | | 0 | // | | * | | = | | // | |1| |Omega| + |Identity|/Gamma | | |Alpha| | | |Y| | CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1); for(int i = 1; i <= KernelNumber; i++) { for(int j = 1; j <= KernelNumber; j++) { MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]); } } MATRIX[0].Set(0, 0); for(int i = 1; i <= KernelNumber; i++) { MATRIX[i].Set(0, 1); MATRIX[0].Set(i, 1); } double B[]; ArrayResize(B, KernelNumber + 1); B[0] = 0; for(int j = 1; j <= KernelNumber; j++) { B[j] = Y[j - 1]; } int info; CDenseSolverLSReport rep; double x[]; CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x); Beta = x[0]; ArrayResize(Alpha, KernelNumber); ArrayCopy(Alpha, x, 0, 1); return true; }
Главный метод класса для выполнения регрессии — process. Из него запускается формирование входных/выходных данных, нормализация, расчет матрицы "омега", решение системы уравнений и получение ошибки по выборке.
bool process() { if(!buildXYVectors()) return false; normalizeXYVectors(); // least squares linear regression for demo purpose only if(KernelNumber == -1 || KernelNumber > VectorNumber) { return regress(); } if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM { buildOmega(); } else // proposed SOM-LS-SVM { if(!buildKernels()) return false; } if(!solveSoLE()) return false; LSSVM_Error result; checkAll(result); ErrorPrint(result); return true; }
Для оценки качества оптимизации в классе используется несколько разных показателей, автоматически рассчитываемых для всего набора данных: среднеквадратическая ошибка, коэффициент корреляции, коэффициент детерминации (R-squared) и % совпадения по знаку (имеет смысл только в режимах с дифференцированием). Все показатели сведены в структуру LSSVM_Error:
struct LSSVM_Error { // indices: 0 - training set, 1 - test set double RMSE[2]; // RMSE double CC[2]; // Correlation Coefficient double R2[2]; // R-squared double PCT[2]; // % };
Нулевой индекс массивов соответствует обучающей выборке, первый — тестовой выборке. Желательно было бы использовать более строгую оценку статистической значимости прогноза, например, критерий Фишера, так как красивые значения корреляция или R2 могут быть обманчивы, но охватить всё сразу не представляется возможным.
Метод расчета ошибки по всей выборке — checkAll.
void checkAll(LSSVM_Error &result) { result.RMSE[0] = result.RMSE[1] = 0; result.CC[0] = result.CC[1] = 0; result.R2[0] = result.R2[1] = 0; result.PCT[0] = result.PCT[1] = 0; double xy = 0; double x2 = 0; double y2 = 0; int correct = 0; double out[]; getResult(out); for(int i = 0; i < VectorNumber; i++) { double given = Y[i]; double trained = out[i]; result.RMSE[0] += (given - trained) * (given - trained); // mean is 0 after normalization xy += (given) * (trained); x2 += (given) * (given); y2 += (trained) * (trained); if(given * trained > 0) correct++; } result.R2[0] = 1 - result.RMSE[0] / x2; result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber); result.CC[0] = xy / sqrt(x2 * y2); result.PCT[0] = correct * 100.0 / VectorNumber; crossvalidate(result); // fill metrics for test set (if attached) }
Перед циклом вызван метод getResult, который выполняет аппроксимацию для всех входных векторов и заполняет этими значениями массив out.
void getResult(double &out[], const bool reverse = false) const { double data[]; ArrayResize(out, VectorNumber); for(int i = 0; i < VectorNumber; i++) { vector(i, data); out[i] = approximate(data); } if(reverse) ArrayReverse(out); }
Здесь используется штатная функция прогнозирования для уже построенной модели — approximate:
double approximate(const double &x[]) const { double sum = 0; double data[]; if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference) { for(int i = 0; i < ArraySize(x); i++) { sum += Solution[i] * x[i]; } sum += Solution[ArraySize(x)]; } else { if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM { for(int i = 0; i < VectorNumber; i++) { vector(i, data); sum += Alpha[i] * kernel(x, data); } } else // proposed SOM-LS-SVM { for(int i = 0; i < KernelNumber; i++) { ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize); sum += Alpha[i] * kernel(x, data); } } } return sum + Beta; }
В ней найденные коэффициенты Alpha[] и Beta применяются к сумме ядерных функций (случаи LS-SVM и SOM-LS-SVM).
Тестовая выборка формируется аналогично обучающей — с помощью еще одного объекта LSSVM, причем в основном объекте задается привязка к "проверочному".
protected: LSSVM *crossvalidator; public: bool bindCrossValidator(LSSVM *tester) { if(tester.getVectorSize() == VectorSize) { crossvalidator = tester; return true; } return false; } void crossvalidate(LSSVM_Error &result) { const int vectorNumber = crossvalidator.getVectorNumber(); double out[]; double _Y[]; crossvalidator.getY(_Y); // assumed normalized by validator double xy = 0; double x2 = 0; double y2 = 0; int correct = 0; for(int i = 0; i < vectorNumber; i++) { crossvalidator.vector(i, out); double z = approximate(out); result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z); xy += (_Y[i]) * (z); x2 += (_Y[i]) * (_Y[i]); y2 += (z) * (z); if(_Y[i] * z > 0) correct++; } result.R2[1] = 1 - result.RMSE[1] / x2; result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber); result.CC[1] = xy / sqrt(x2 * y2); result.PCT[1] = correct * 100.0 / vectorNumber; }
Класс позволяет при необходимости выполнить вместо нелинейной оптимизации по алгоритму LS-SVM/SOM-LS-SVM линейную регрессию методом наименьших квадратов в системе с VeсtorSize переменных и VectorNumber уравнений. Для этого реализован метод regress.
bool regress(void) { CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column for(int i = 0; i < VectorNumber; i++) { MATRIX[i].Set(VectorSize, Y[i]); } for(int i = 0; i < VectorSize; i++) { for(int j = 0; j < VectorNumber; j++) { MATRIX[j].Set(i, X[j * VectorSize + i]); } } CLinearModel LM; CLRReport AR; int info; CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR); if(info != 1) { Alert("Error in regression model!"); return false; } int _size; CLinReg::LRUnpack(LM, Solution, _size); Print("RMSE=" + (string)AR.m_rmserror); ArrayPrint(Solution); return true; }
Этот метод заведомо проигрывает в точности LS-SVM и добавлен для демонстрации этого. С другой стороны, он может быть востребован для регрессии более простых по своей природе данных, чем котировки. Включение этого режима происходит при задании KernelNumber = -1. В этом случае решение записывается в массив Solution (Alpha[] и Beta при этом не участвуют).
Создадим на основе класса LSSVM прогнозирующий индикатор.
Прогнозирующий индикатор LS-SVM
Задача индикатора SOMLSSVM.mq5 — создать 2 объекта LSSVM (один для обучающей выборки, другой для тестовой), выполнить регрессию и отобразить исходные и спрогнозированные значения с оценкой качества прогноза в обоих выборках. Параметры "гамма" и "сигма" будут считаться уже подобранными и задаваться пользователем. Их оптимизацию удобнее проводить в эксперте с помощью штатного тестера (этому будет посвящен следующий раздел). В принципе, тестер мог бы поддерживать возможность оптимизировать и индикаторы, т.к. данное ограничение носит искусственный характер. Тогда мы могли бы оптимизировать модель непосредственно в индикаторе.
В индикаторе будет 4 буфера в отдельном окне. 2 буфера отобразят исходные и спрогнозированные значения для обучающей выборки, а 2 других буфера — то же самое для тестовой.
Входные параметры:
input int _VectorNumber = 250; // VectorNumber (training) input int _VectorNumber2 = 50; // VectorNumber (validating) input int _VectorSize = 20; // VectorSize input double _Gamma = 0; // Gamma (0 - auto) input double _Sigma = 0; // Sigma (0 - auto) input int _KernelNumber = 0; // KernelNumber (0 - auto) input int _TrainingOffset = 50; // Offset of training bars input int _ValidationOffset = 0; // Offset of validation bars input int DifferencingOrder = 1;
Два первых задают размер обучающей и тестовой выборки. Размер вектора указывается в VectorSize. Параметры Gamma и Sigma можно оставить равными 0 для автоматического выбора их значений на основе входных данных, но качество этого тривиального режима далеко от оптимального — он нужен только для того, чтобы индикатор работал со значениями по умолчанию. KernelNumber следует оставить равным 0 для регрессии методом LS-SVM. Тестовый набор по умолчанию расположен в самом конце истории котировок, а обучающий слева от него (хронологически раньше).
На основе входных параметров производится инициализация объектов.
LSSVM *lssvm = NULL; LSSVM *test = NULL; int OnInit() { static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"}; for(int i = 0; i < BUF_NUM; i++) { PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE); PlotIndexSetString(i, PLOT_LABEL, titles[i]); } lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset); test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset); lssvm.setDifferencingOrder(DifferencingOrder); test.setDifferencingOrder(DifferencingOrder); return INIT_SUCCEEDED; }
Вычисление индикатора происходит лишь однажды, так как он создан в демонстрационных целях. При необходимости его легко адаптировать так, чтобы показания обновлялись на каждом баре, но потенциально накладное решение системы следует выполнить лишь раз или повторять через определенный довольно большой период времени.
int OnCalculate(const int rates_total, const int prev_calculated, const datetime& Time[], const double& Open[], const double& High[], const double& Low[], const double& Close[], const long& Tick_volume[], const long& Volume[], const int& Spread[]) { ArraySetAsSeries(Open, true); ArraySetAsSeries(Time, true); static bool calculated = false; if(calculated) return rates_total; calculated = true; for(int k = 0; k < BUF_NUM; k++) { buffers[k].empty(); } lssvm.bindCrossValidator(test); bool processed = lssvm.process(true);
В обработчике OnCalculate мы подключаем тестовый набор к обучающему и запускаем регрессию. Если она завершится успешно, отображаем все данные: как исходные, так и полученные прогнозы:
if(processed) { const double m1 = lssvm.getMean(); const double s1 = lssvm.getStdDev(); const double m2 = test.getMean(); const double s2 = test.getStdDev(); // training double out[]; lssvm.getY(out, true); for(int i = 0; i < _VectorNumber; i++) { out[i] = out[i] * s1 + m1; } buffers[0].set(_TrainingOffset, out); lssvm.getResult(out, true); for(int i = 0; i < _VectorNumber; i++) { out[i] = out[i] * s1 + m1; } buffers[1].set(_TrainingOffset, out); // validation test.getY(out, true); for(int i = 0; i < _VectorNumber2; i++) { out[i] = out[i] * s2 + m2; } buffers[2].set(_ValidationOffset, out); for(int i = 0; i < _VectorNumber2; i++) { test.vector(i, out); double z = lssvm.approximate(out); z = z * s2 + m2; buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z; ... } }
Поскольку у нас есть опция анализа дифференцированного ряда, индикатор выводится в отдельном окне. Однако по сути мы все равно работаем с ценами и желательно отобразить прогноз на основном графике. Для этого можно использовать объекты. Их координаты по оси цен следует восстановить из разностного ряда. Индексация элементов в исходном ряду и в производных от него разностных рядах различного порядка иллюстрируется следующей схемой (индексация в порядке хронологии):
d0: 0 1 2 3 4 5 :y
d1: 0 1 2 3 4
d2: 0 1 2 3
d3: 0 1 2
Например, если разность первого порядка (d1), то очевидно, что:
y[i+1] = y[i] + d1[i]
Для разностей второго (d2) и третьего (d3) порядков уравнения будут такими:
y[i+2] = 2 * y[i+1] - y[i] + d2[i]
y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]
Мы видим, что чем больше порядок дифференцирования, тем большее количество предыдущих отсчетов y участвует в расчетах.
Применив данные формулы, мы можем изобразить прогноз объектами на графике цены.
if(ShowPredictionOnChart) { double target = 0; if(DifferencingOrder == 0) { target = z; } else if(DifferencingOrder == 1) { target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z; } else if(DifferencingOrder == 2) { target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z; } else if(DifferencingOrder == 3) { target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z; } else { // unsupported yet } string name = prefix + (string)i; ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target); ObjectSetString(0, name, OBJPROP_TEXT, "l"); ObjectSetString(0, name, OBJPROP_FONT, "Wingdings"); ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER); ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed); }
Порядки выше 3 не рассматривались, так как они имеют не только положительный, но и один негативный эффект. Напомним, что положительный заключается в том, что качество прогноза повышается с увеличением порядка за счет возрастающей стационарности. Однако это относится именно к прогнозу производной соответствующего порядка, а не к исходному ряду. Негативный эффект дифференцирования высоких порядков в том, что на них даже очень мелкая ошибка существенно возрастает при последующем "разворачивании" приращений в интегрированный ряд. Таким образом, для параметра DifferencingOrder также следует найти "золотую середину" путем оптимизации или подбора.
Оба эффекта можно наблюдать на двух следующих скриншотах (светлозеленая и зеленая линии - реальные данные обучающей и тестовой выборок; голубая и синяя линии - прогноз на обучающей и тестовой выборках):
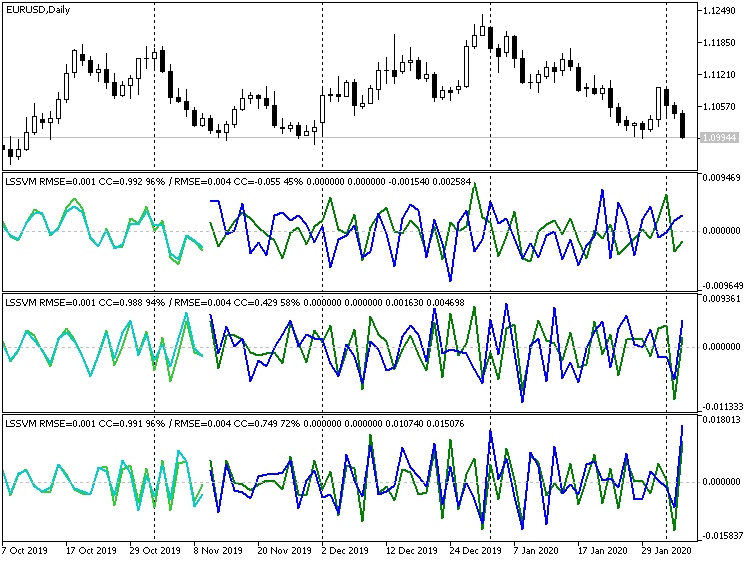
Индикаторы LSSVM с различным порядком дифференцирования ряда EURUSD D1
Здесь показано 3 экземпляра индикатора с общими настройками и с разными порядками дифференцирования. Общие настройки:
- _VectorNumber = 250; // VectorNumber (training)
- _VectorNumber2 = 60; // VectorNumber (validating)
- _VectorSize = 20; // VectorSize
- _Gamma = 2048; // Gamma (0 - auto)
- _Sigma = 8; // Sigma (0 - auto)
- _KernelNumber = 0; // KernelNumber (0 - auto)
- _TrainingOffset = 60; // Offset of training bars
- _ValidationOffset = 0; // Offset of validation bars
Порядок дифференцирования равен, соответственно, 1, 2 и 3. В заголовке каждого окна после наклонной черты выведены показатели прогноза для тестовой (в данном случае — валидационной) выборки: они увеличиваются в лучшую сторону (коэффициент корреляции: -0.055, 0.429, 0.749; процент совпадающих знаков приращений: 45%, 58%, 72%). В принципе, улучшение совпадения линий видно даже визуально. Однако, если мы восстановим прогноз третьего порядка на график цены, получим такую картину:
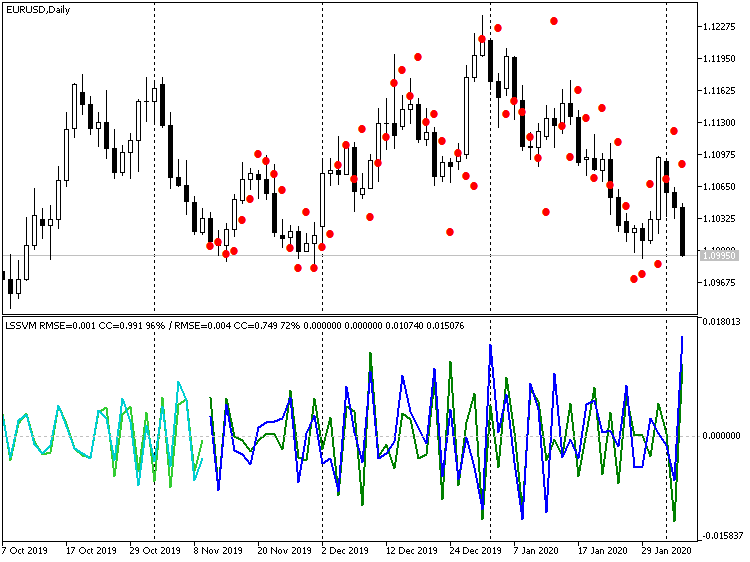
Индикатор LSSVM третьего порядка дифференцирования с восстановленными значениями прогноза цен EURUSD D1
Очевидно, что многие точки можно охарактеризовать как выбросы. С другой стороны, если дифференцирование отключить совсем, получим:
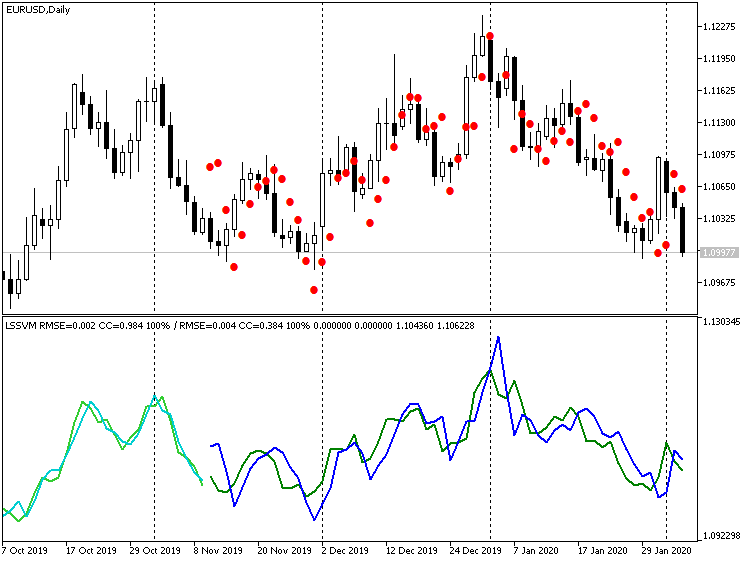
Индикатор LSSVM без дифференцирования с восстановленными значениями прогноза цен EURUSD D1
Здесь значения цены гораздо ближе к реальным, но заметно отставание прогноза по фазе примерно на 1 бар. Этот эффект объясняется тем, что наш алгоритм фактически эквивалентен цифровому фильтру, своего рода скользящей средней на основе N векторов-образцов. Учитывая близость по уровню цен, данную задержку в 1-2 бара имеет смысл нивелировать за счет прогнозирования сразу на несколько шагов вперед, т.е. после получения прогноза для -1 бара, подавать его как входной отсчет для прогноза -2 бара и так далее. Мы предусмотрим данный режим при создании эксперта в следующем разделе.
Эксперт LS-SVM
Эксперт LSSVMbot.mq5 служит для выполнения двух задач:
- оптимизация параметров "гамма" и "сигма" LS-SVM в виртуальном режиме (без торговли);
- торговля в тестере и опционально оптимизация прочих параметров в режиме торговли;
В виртуальном режиме, также как и в индикаторе, используется 2 экземпляра LSSVM — один с обучающей выборкой, а второй — с тестовой. Именно показатели тестовой выборки и берутся в расчет. Оптимизация проводится по пользовательскому критерию. Все они сведены в перечисление:
enum CUSTOM_ESTIMATOR { RMSE, // RMSE CC, // correlation R2, // R-squared PCT, // % TRADING // trading };
Вариант TRADING применяется для перевода эксперта в режим торговли. В нем эксперт можно оптимизировать привычным способом по одному из встроенных критериев (прибыль, просадка и т.д.).
Основная группа входных параметров задает те же величины, что и в индикаторе.
input int _VectorNumber = 250; // VectorNumber (training) input int _VectorNumber2 = 25; // VectorNumber (validating) input int _VectorSize = 20; // VectorSize input double _Gamma = 0; // Gamma (0 - auto) input double _Sigma = 0; // Sigma (0 - auto) input int _KernelNumber = 0; // KernelNumber (sqrt, 0 - auto) input int DifferencingOrder = 1; input int StepsAhead = 0;
Однако смещения TrainingOffset и ValidationOffset стали внутренними переменными и устанавливаются автоматически. ValidationOffset всегда равен 0. TrainingOffset равен размеру тестовой выборки VectorNumber2 в виртуальном режиме, или 0 в режиме торговли (поскольку здесь подразумевается, что все параметры уже найдены, тестовой выборки нет, и проводить регрессию следует по свежим данным).
Для использования SOM в параметре KernelNumber нужно указать размер одной стороны, а полный размер карты будет вычислен как квадрат этого значения.
Для оптимизации "гамма" и "сигма" предназначена вторая группа входных параметров:
input int _GammaIndex = 0; // Gamma Power Iterator input int _SigmaIndex = 0; // Sigma Power Iterator input double _GammaStep = 0; // Gamma Power Multiplier (0 - off) input double _SigmaStep = 0; // Sigma Power Multiplier (0 - off) input CUSTOM_ESTIMATOR Estimator = R2;
Поскольку диапазон поиска очень широк, а штатный тестер поддерживает итерацию только путем прибавления заданного шага, в эксперте применен следующий подход. Оптимизация должна быть включена по параметрам GammaIndex и SigmaIndex. Каждый из них определяет, какое количество раз нужно умножить начальные значения Gamma и Sigma, на множители GammaStep и SigmaStep соответственно, чтобы получить рабочее значение "гамма" и "сигма". Например, если Gamma равна 1, GammaStep равно 2, и оптимизация проводится для GammaIndex в диапазоне от 0 по 5, то алгоритм оценит значения "гаммы" 1, 2, 4, 8, 16, 32. Если GammaStep и SigmaStep не равны 0, они всегда используются для вычисления рабочего значения "гамма" и "сигма", в том числе и в одиночном прогоне тестера.
Эксперт работает по барам. Эксперт начинает вычисления не ранее, чем в истории будет доступно запрошенное количество баров (векторов). Если в тестере не окажется достаточного количества баров, прогон может закончиться вхолостую — смотрите логи. К сожалению, количество баров истории, подгружаемых тестером при старте, зависит от многих факторов (таймфрейма, номера дня внутри года и пр.) и может существенно варьироваться. При необходимости отодвигайте начальное время теста в прошлое.
В виртуальном режиме обучение модели происходит лишь единожды и одна из характеристик (выбранная в параметре Estimator) возвращается из функции OnTester как показатель качества (в случае выбора RMSE, ошибка отдается с обратным знаком).
bool optimize() { if(Estimator != TRADING) lssvm.bindCrossValidator(test); iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep); bool success = lssvm.process(); if(success) { LSSVM::LSSVM_Error result; lssvm.checkAll(result); Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma()); Print(" training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]); Print(" test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]); customResult = Estimator == CC ? result.CC[1] : (Estimator == RMSE ? -result.RMSE[1] // the lesser |absolute error value| the better : (Estimator == PCT ? result.PCT[1] : result.R2[1])); } return success; } void OnTick() { ... if(Estimator != TRADING) { if(!processed) { processed = optimize(); } } ... } double OnTester() { return processed ? customResult : -1; }
В режиме торговли обучение модели происходит по умолчанию также лишь один раз, но можно задать перестроение каждый год, квартал или месяц. Для этого в параметре OPTIMIZATION (в коде он называется _2) следует написать, соответственно "y", "q" или "m" (верхний регистр также поддерживается). Напомним, что данный процесс затрагивает только решение системы уравнений по новым (свежим) данным, однако параметры "гамма" и "сигма" остаются прежними. В принципе, можно усложнить процесс и при каждом переобучении налету подбирать параметры (то, что мы ранее поручили штатному оптимизатору), однако тогда это должно быть организовано внутри эксперта и потому будет выполняться единственным потоком.
Сейчас подразумевается, что параметры "гамма" и "сигма", подобранные для данных за достаточно долгий период (год и более) не должны терять своей актуальности в течение торговых периодов меньшей длительности.
После того как модель построена, тестовый экземпляр LSSVM используется для чтения последних известных цен, формирования из них входного вектора, и его нормализации. Далее вектор передается в метод lssvm.approximate:
static bool solved = false; if(!solved) { const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0); solved = opt ? optimize() : lssvm.process(); } if(solved) { // test is used to read latest _VectorNumber2 prices if(!test.buildXYVectors()) { Print("No vectors"); return; } test.normalizeXYVectors(); double out[]; // read latest vector if(!test.buildVector(out)) { Print("No last price"); return; } test.normalizeVector(out); double z = lssvm.approximate(out);
В зависимости от входного параметра StepsAhead, эксперт либо сразу пускает полученное значение z в дело, преобразуя его в предсказание цены путем денормализации, либо заданное количество раз повторяет прогноз и только затем преобразует в цену.
for(int i = 0; i < StepsAhead; i++) { ArrayCopy(out, out, 0, 1); out[ArraySize(out) - 1] = z; z = lssvm.approximate(out); } z = test.denormalize(z);
Поскольку временной ряд мог быть дифференцированным, мы берем несколько последних значений цены, чтобы восстановить по ним и прогнозному приращению следующее значение цены.
double open[]; if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current { double target = 0; if(DifferencingOrder == 0) { target = z; } else if(DifferencingOrder == 1) { target = open[2] + z; } else if(DifferencingOrder == 2) { target = 2 * open[2] - open[1] + z; } else if(DifferencingOrder == 3) { target = 3 * open[2] - 3 * open[1] + open[0] + z; } else { // unsupported yet }
В зависимости от положения спрогнозированной цены относительно текущего уровня, эксперт открывает сделку. Если позиция в нужном направлении уже открыта, она сохраняется. Если позиция в противоположном направлении, делается переворот.
int mode = target >= open[2] ? +1 : -1; int dir = CurrentOrderDirection(); if(dir * mode <= 0) { if(dir != 0) // there is an order { OrdersCloseAll(); } if(mode != 0) { const int type = mode > 0 ? OP_BUY : OP_SELL; const double p = type == OP_BUY ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID); OrderSend(_Symbol, type, Lot, p, 100, 0, 0); } } } }
Проверим как эксперт функционирует в обоих режимах. В качестве рабочего инструмента возьмем XAUUSD, как менее подверженного национальным новостям (по сравнению с валютами). Таймфрейм — D1.
Файл с настройками прилагается (LSSVMbot.set). Размер обучающего набора VectorNumber волюнтаристски выбран равным 200. Это чуть меньше года. Большие значения в районе 1000 могут уже существенно замедлить решение системы уравнений. Тестовый набор VectorNumber2=50. Размер вектора VectorSize=20 (месяц). SOM не используется (KernelNumber=0). Дифференцирование отключено (DifferencingOrder=0), но для стадии проверки в торговом режиме стоит прогнозирование на 2 шага вперед (StepsAhead=2), поскольку с помощью индикатора мы заметили незначительное отставание прогноза от цен. В виртуальном режиме при расчете модели входной параметр StepsAhead не используется.
Базовые значения Gamma и Sigma равны 1, но их множители Power Multiplier (GammaStep, SigmaStep) равны 2, а количество умножений, которые будут производиться в процессе оптимизации, заданы в итераторах GammaIndex и SigmaIndex, соответственно, как интервалы от 5 до 35 и от 5 до 20 с шагом 5. Таким образом, когда GammaIndex будет равно 15, Gamma получит значение равное 1 * (2 в степени 15), то есть 32768.
Подбор правильных диапазонов для поиска "гамма" и "сигма" — довольно рутинная задача, т.к. для неё, к сожалению, не существует иного решения кроме расчетов сперва по грубой сетке, а затем по более мелкой. Мы ограничимся одной сеткой, т.к. при подготовке статьи было сделано много проб, которые можно считать поиском в более широком диапазоне.
Итак, оптимизируемых параметров всего 2: GammaIndex и SigmaIndex. Они опосредованно меняют Gamma и Sigma в большом диапазоне, с переменным шагом в геометрической прогрессии.
Запустим оптимизацию на 2018 году, по ценам открытия. Оптимизацию делаем по пользовательскому критерию, Estimator = R2.
Напомним, что эксперт в этом режиме не торгует, а заполняет из котировок систему уравнений и решает её по алгоритму LS-SVM. В расчете участвуют бары в количестве, достаточном, чтобы сформировать VectorNumber векторов размера VectorSize с поправкой на возможно включенное дифференцирование (каждый дополнительный порядок взятия разниц требует дополнительного бара во входных данных). Кроме того, эксперту дополнительно требуется VectorNumber2 тестовых векторов, которые хронологически располагаются после обучающих, то есть на самых последних барах. Именно на тестовых барах (точнее, сформированных из них векторах) оцениваются прогностические способности полученной модели для возврата из OnTester.
Все это важно, поскольку тестер не всегда имеет достаточное количество баров в истории при старте, и эксперт сможет заполнить систему лишь несколько меяцев спустя начальной даты. С другой стороны, не стоит забывать, что обучающие бары всегда начинаются раньше даты теста (оптимизации), так как эксперту сразу предоставляется история некоторой длины.
После завершения оптимизации отсортируем результаты по критерию R2 (по убыванию, т.е. лучшие вверху). Допустим, в начале будут идти настройки GammaIndex=15 и SigmaIndex=5 (сказано "допустим", потому что порядок проходов с равными результатами, вероятно, может меняться).
Выполним двойной щелчок мыши на первой записи, чтобы запустить одиночный тест (пока еще в виртуальном режиме). В логе увидим примерно следующее:
2018.01.01 00:00:00 Bars required: 270 2018.01.02 00:00:00 247 2017.01.03 00:00:00 2018.02.02 00:00:00 Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270 2018.02.02 00:00:00 G[15]=32768.0 S[5]=32.0 2018.02.02 00:00:00 RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985 2018.02.02 00:00:00 Parameters: 32768.0 32.0 2018.02.02 00:00:00 training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0 2018.02.02 00:00:00 test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0 final balance 10000.00 USD OnTester result 0.9598497541714557
Это можно трактовать следующим образом: для выполнения полной процедуры требовалось 270 баров, но в момент старта 2018.01.02 в наличии было только 247. Достаточное количество появилось только 2018.02.02 (то есть месяц спустя), причем обучающие данные (доступная история) начинались 2017.01.03. Далее указаны рабочие параметры Gamma и Sigma (G[15]=32768.0 S[5]=32.0, в квадратных скобках — оптимизированные параметры-итераторы). Наконец, в строке с показателями качества обучения видим величину R2 (0.95985), которая и была возвращена из OnTester.
Теперь отключим оптимизацию, расширим диапазон дат с 2017 до февраля 2020, в параметрах эксперта установим Estimator = TRADING (это означает, что эксперт будет совершать торговые операции). В параметре OPTIMIZATION (в коде — _2) введем символ "q", что предписывает эксперту раз в квартал пересчитывать регрессионную модель на новых данных (последних на текущий момент VectorNumber векторов). Но "гамма" и "сигма" при этом остаются прежними.
Запустим одиночный тест.
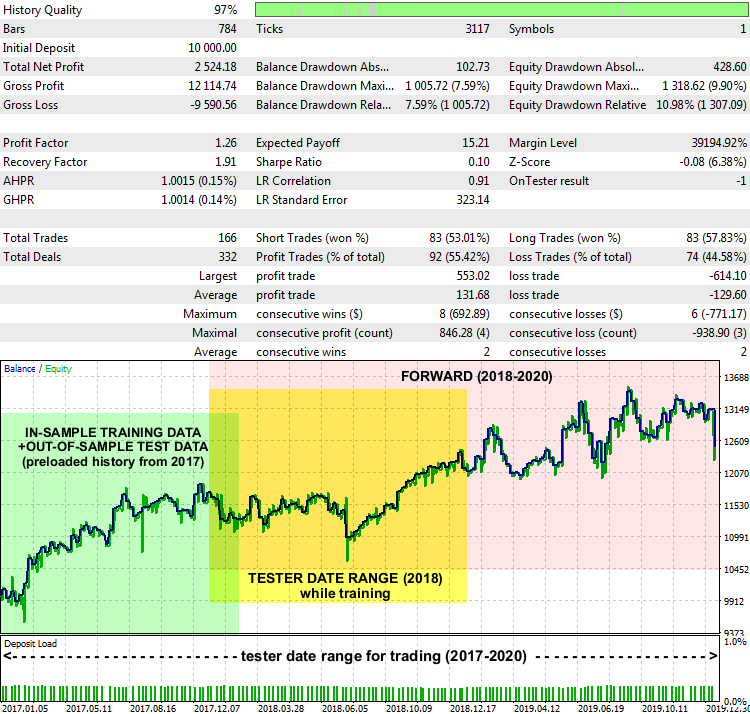
Отчет эксперта LSSVMbot на XAUUSD D1, 2017-2020
Показатели невыдающиеся, но система в целом работает. На графике отчета помечены диапазоны дат, откуда брались обучающие данные для нахождения оптимальных "гамма" и "сигма" (подсвечено зеленым), какой диапазон был задан в тестере в режиме обучения (подсвечено желтым), и диапазон, где эксперт торговал на незнакомых данных (подсвечено розовым).
Способ интерпретации прогноза и построение вокруг него торговой стратегии может быть разным. В частности, в нашем тестовом эксперте есть входной параметр PreviousTargetCheck (по умолчанию false). Если его включить, то торговля по прогнозу будет вестись с помощью другой стратегии: направление сделки определяется относительным положением свежего прогноза относительно предыдущего. Также остается простор для экспериментов с другими настройками, например, с кластеризацией SOM, изменением лота в зависимости от силы прогнозируемого движения, доливками, и т.д.
Заключение
В данной статье мы познакомились с алгоритмом прогнозирования временных рядов на базе LS-SVM, требующим активного применения математического аппарата и тщательной настройки. Успешное использование подобных методов (EMD из первой части и LS-SVM из данной, второй) на практике может сильно зависеть от особенностей временных рядов, а в приложении к трейдингу — от природы финансового инструмента и таймфрейма. Поэтому выбор рынка, соответствующего возможностям конкретного алгоритма, не менее важен, чем реализация наукоемких и/или ресурсоемких вычислений. В частности, валюты Форекс менее предсказуемы и более подвержены внешним шокам, что снижает эффективность прогноза, строящегося исключительно на исторических котировочных данных. Более подходящими для двух рассмотренных методов следует считать металлы, индексы или сбалансированные корзины (портфели). Кроме того, каким-бы замечательным ни казался прогноз, не следует забывать об управлении рисками, защитных стоп-приказах, мониторинге новостного фона.
Предоставленные исходные коды позволяют встроить новые методы в собственные проекты MQL.
 Применение OLAP в трейдинге (Часть 4): Количественный и визуальный анализ отчетов тестера
Применение OLAP в трейдинге (Часть 4): Количественный и визуальный анализ отчетов тестера
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования