
Explorando os Padrões Sazonais de Séries Temporais Financeiras com o Boxplot
Tentativa de refutar a hipótese do mercado eficiente e provar a existência de ciclos de mercado
Em 2013, Eugene Fama, que desenvolveu a hipótese do mercado eficiente, ganhou o Prêmio Nobel de Economia. De acordo com sua hipótese, os preços dos ativos refletem completamente todas as informações substanciais. Isso significa que nenhum dos participantes de mercado tem vantagens sobre os outros.
No entanto, a hipótese em si tem algumas ressalvas, enquanto a eficiência pode ter os seguintes três níveis:
- fraco se o preço do ativo de mercado refletir completamente as informações passadas sobre esse ativo
- médio quando o preço refletir não apenas o passado, mas também as informações públicas atuais
- forte, quando ele refletir adicionalmente as informações privilegiadas não públicas
Dependendo do grau de eficiência, os mercados possuem diferentes graus de previsibilidade. Para um analista técnico, isso significa que podem existir diferentes componentes sazonais cíclicos no mercado.
Por exemplo, a atividade de mercado pode variar de ano para ano, de mês para mês, de sessão para sessão, de hora em hora e assim por diante. Além disso, esses ciclos podem representar algumas sequências previsíveis, dentro e entre as quais o profissional pode encontrar seu alfa. Os ciclos também podem se sobrepor e criar diferentes padrões de composição que podem ser mais explorados.
Busca por padrões sazonais nos incrementos de preço
Nós podemos estudar os ciclos regulares junto com os compostos. Vamos ver o exemplo do estudo das flutuações mensais de um instrumento financeiro. Para esse fim, nós usaremos a linguagem IPython combinado com a plataforma MetaTrader 5.
Para facilitar a importação das cotações diretamente do terminal, nós usaremos o seguinte código:
from MetaTrader5 import * from datetime import datetime import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import seaborn; seaborn.set() # Initializing MT5 connection MT5Initialize("C:\\Program Files\\MetaTrader 5\\terminal64.exe") MT5WaitForTerminal() print(MT5TerminalInfo()) print(MT5Version())
Aqui, devemos especificamos o caminho da sua plataforma, que pode diferir do meu.
Adicionamos mais algumas linhas para iniciar a análise:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
returns.head(5)
Monthly_Returns = returns.groupby([returns.index.year.rename('year'), returns.index.month.rename('month')]).mean()
Monthly_Returns.boxplot(column='close', by='month', figsize=(15, 8))
A variável rates recebe o dataframe do pandas com os preços no intervalo de tempo especificado (por exemplo, 10 anos neste exemplo). Suponha que nós estamos interessados apenas nos preços de fechamento (para simplificar outras interpretações). Vamos excluir as colunas de dados desnecessárias usando o método rates.drop().
Os preços alteram o seu valor médio ao longo do tempo e formam tendências, portanto, a análise estatística não é aplicável a essas séries brutas. As variações percentuais dos preços (incrementos de preços) geralmente são usadas na econometria para garantir que todas estejam na mesma faixa de valor. As alterações percentuais podem ser recebidas usando o método pd.DataFrame(rates['close'].pct_change(1)).
Nós precisamos das médias do preço mensais. Vamos organizar a tabela para receber os valores médios dos incrementos mensais por ano e exibi-los no diagrama do boxplot.
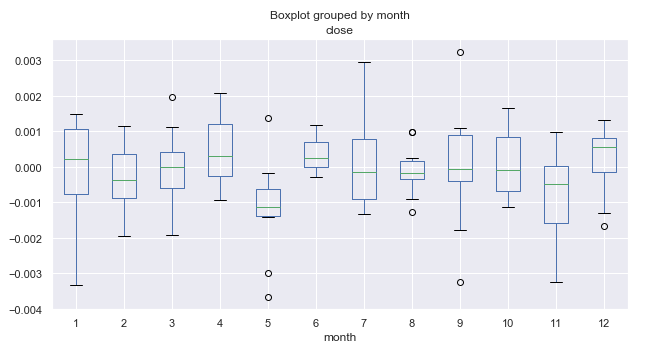
Fig. 1. Média dos preços em intervalos mensais dos últimos 10 anos.
O que são os boxplots e como interpretá-los?
Nós precisamos acessar os dados sobre a volatilidade ou a distribuição dos dados de preços por um período selecionado. Cada boxplot separado (ou diagrama de caixa) fornece uma boa visualização de como os valores são distribuídos ao longo do conjunto de dados. Os boxplots não devem ser confundidos com os gráficos de velas, embora possam ser visualmente semelhantes. Ao contrário das velas, os boxplots fornecem uma maneira padronizada de exibir a distribuição dos dados com base em cinco leituras.
- A mediana, o Q2 ou o 50º percentil mostra o valor médio do conjunto de dados. O valor aparece como uma linha verde horizontal dentro das caixas no diagrama.
- O primeiro quartil, Q1 (ou o 25º percentil) representa a mediana entre Q2 e o menor valor da amostra, que cai dentro do intervalo de confiança de 99%. Ele é exibido como a borda inferior da caixa "corpo" no diagrama.
- O terceiro quartil, Q3 (ou o 75º percentil) é a mediana entre Q2 e o valor máximo, exibido como a borda superior da caixa "corpo".
- O corpo da caixa forma um intervalo interquartil (entre os 25º e 75º percentis), também chamado de IQR.
- O whisker ou fio de bigode da caixa complementam a distribuição. Eles cobrem 99% de toda a variação da amostra, e os pontos acima e abaixo indicam os valores além da faixa de 99%.
Esses dados são suficientes para avaliar a faixa de flutuações e a dispersão de valores dentro da faixa interna.
Análise mais aprofundada dos padrões sazonais
Vamos considerar a figura 1 em mais detalhes. Nós podemos ver que a mediana dos incrementos para o quinto mês (maio) é deslocada para baixo em relação ao zero e tem um valor atípico visível acima de zero. Em geral, como nós podemos ver pelas estatísticas de 10 anos, o mercado em maio estava em baixa em relação a março. Houve apenas um ano, quando o mercado cresceu em maio. Essa é uma ideia interessante, que está de acordo com o ditado do trader "Venda em maio e vá embora!".
Vamos dar uma olhada no 6º mês (junho), seguinte ao mês de maio. Quase sempre (com exceção de um ano) o mercado estava crescendo em junho em relação a maio, mostrando um padrão que se repete a cada ano. A variação das flutuações de junho é bastante pequena, sem discrepâncias (ao contrário de maio), o que indica uma boa estabilidade sazonal.
Preste atenção ao 11º mês (novembro). A probabilidade de o mercado cair durante esse período é alta. Depois disso, em dezembro, o mercado voltou a subir. Janeiro (1º mês) foi marcado por uma alta volatilidade e queda em relação a dezembro.
Os dados obtidos podem fornecer uma visão geral das condições subjacentes para a tomada de decisões de negociação. Além disso, as probabilidades podem ser integradas em um sistema de negociação. Por exemplo, ele pode realizar mais compras ou vendas em determinados meses.
Os dados do ciclo mensal são muito interessantes, mas é possível analisar ainda mais profundamente os ciclos diários mais curtos.
Vamos ver a distribuição dos incrementos dos preços para cada dia da semana separado, usando o mesmo período de 10 anos:
Daily_Returns = returns.groupby([returns.index.week.rename('week'), returns.index.dayofweek.rename('day')]).mean()
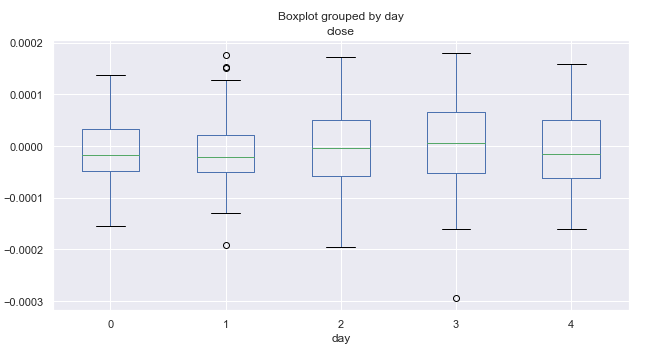
Fig. 2. Média dos preços que varia pelos dias da semana dos últimos 10 anos.
Aqui, o valor zero corresponde a segunda-feira e o valor quatro a sexta-feira. De acordo com a faixa de preço, a volatilidade por dias permanece quase que constante. Não se pode concluir que as negociações sejam mais intensas em um determinado dia da semana. Em média, o mercado está mais inclinado a cair do que nas segundas e sextas-feiras. Talvez, em alguns meses separados, a distribuição por dia tenha uma aparência diferente. Vamos realizar análises adicionais.
# leave only one month "returns.index[~returns.index.month.isin([1])" returns = returns.drop(returns.index[~returns.index.month.isin([1])])
No código acima, 1 é usado para janeiro. Ao alterar esse valor, nós podemos obter as estatísticas para qualquer mês, no nosso caso por 10 anos.
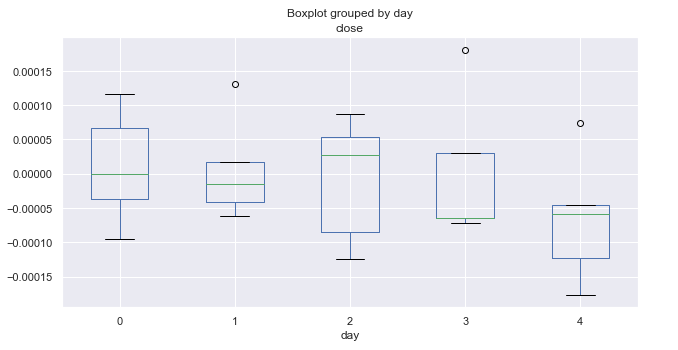
Fig. 3. Média dos preços que varia pelos dias da semana dos últimos 10 anos (janeiro).
O diagrama acima mostra a distribuição dos incrementos por dia para janeiro. Agora, o diagrama fornece os detalhes mais úteis em comparação com o resumo estatístico de todos os meses. Isso mostra claramente que o mercado tende ser de baixa às sextas-feiras. Houve apenas uma ocorrência do par EURUSD não cair (exibido por um valor atípico acima de zero).
Aqui, estão as estatísticas semelhantes para março:
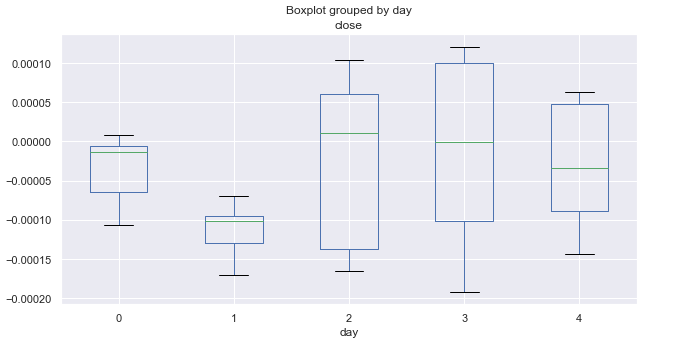
Fig. 4. Média dos preços que varia pelos dias da semana dos últimos 10 anos (março).
As estatísticas de março são completamente diferentes das de janeiro. Segunda e terça-feira (especialmente terça-feira) mostram uma tendência de baixa. Todas as terças-feiras fecharam com uma queda significativa, enquanto os dias restantes flutuam em torno de zero (em média).
Vamos dar uma olhada em outubro:
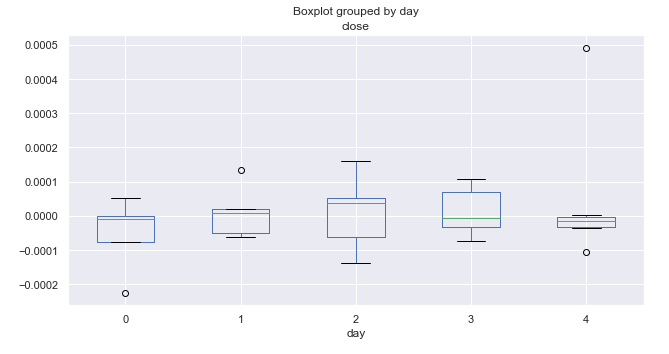
Fig. 5. Média dos preços que varia pelos dias da semana dos últimos 10 anos (outubro).
A análise da distribuição do incremento por dia da semana não revelou padrões de destaque. Nós só podemos destacar quarta-feira, que tem a maior amplitude e potencial para um maior movimento no preço. Todos os outros dias mostram probabilidade iguais para os movimentos para cima e para baixo, contendo alguns valores atípicos.
Análise de padrões sazonais intradiários
Muitas vezes, é necessário levar em consideração as distribuições intradiárias durante a criação de um sistema de negociação, por exemplo, para usar os dados de uma hora (H1), além das distribuições diárias e mensais. Isso pode ser feito facilmente.
Considere a distribuição de incrementos de preço para cada hora:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
Hourly_Returns = returns.groupby([returns.index.day.rename('day'), returns.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(10, 5))
Estas são as cotações do período de 15 minutos por 10 anos. Outra diferença é que os dados são agrupados por dias e horas para obter as medianas horárias de todos os dias na subamostra.
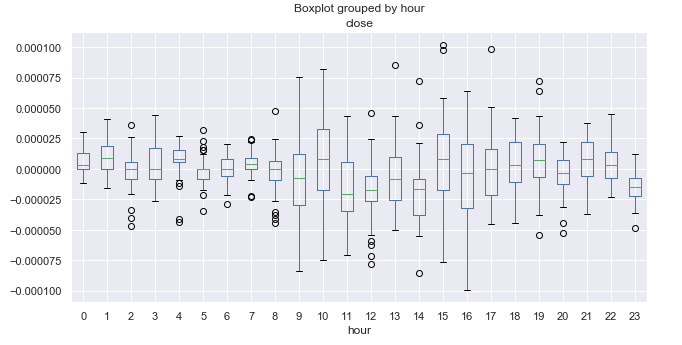
Fig. 6. Média dos preços em intervalos horários dos últimos 10 anos.
Aqui é necessário conhecer o fuso horário da plataforma. No meu caso, é +2. Para referência, vamos escrever os horários de abertura e fechamento das principais sessões do mercado FOREX em UTC+2.
| Sessão | Início | Encerramento |
|---|---|---|
| Pacífico | 21.00 | 08.00 |
| Asiática | 01.00 | 11.00 |
| Europeia | 08.00 | 18.00 |
| Americana | 14.00 | 00.00 |
As negociações durante a sessão do Pacífico geralmente são calmas. Se você observar o tamanho das caixas, poderá perceber facilmente que o intervalo é mínimo entre 21.00-08.00, o que corresponde a operações silenciosas. O intervalo aumenta após a abertura das sessões europeias e americanas e depois começa a diminuir gradualmente. Parece que não há padrões cíclicos óbvios, que eram claros no período diário. O incremento médio varia em torno de zero, sem horas para tendência de alta ou baixa.
Um período interessante acontece as 23.00 (encerramento da sessão americana), durante o qual os preços geralmente decrescem em relação às 22.00. Isso pode ser uma indicação de uma correção no final da sessão. As 00.00, os preços crescem em relação a 23,00, portanto, isso pode ser tratado como uma regularidade. É difícil detectar ciclos mais claros, mas temos uma imagem completa da faixa de preço e sabemos o que esperar no momento.
A inclinação em incrementos com um único atraso pode ocultar alguns padrões. Portanto, seria razoável considerar os dados prejudicados por uma média móvel com um período arbitrário.
Busca por padrões sazonais prejudicados por um MA
Determinar o componente de tendência adequado é muito complicado. Às vezes, as séries temporais podem ser suavizadas demasiadamente. Nesse caso, haverá poucos sinais de negociação. Se o período de suavização for reduzido, a alta frequência de negócios poderá não cobrir o spread e a comissão. Vamos editar o código para eliminar sua tendência usando uma média móvel:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
rates = rates.set_index('time')
# set the moving average period
window = 25
# detrend tome series by MA
ratesM = rates.rolling(window).mean()
ratesD = rates[window:] - ratesM[window:]
plt.figure(figsize=(10, 5))
plt.plot(rates)
plt.plot(ratesM)
O período da média móvel é definido como 25. Este parâmetro, bem como o período para o qual os preços de fechamento são solicitados, podem ser alterados. Eu uso o período gráfico de 15 minutos. Como resultado, nós obtemos o desvio médio dos preços de fechamento da média móvel de 15 minutos para cada hora. Aqui está a série temporal resultante:
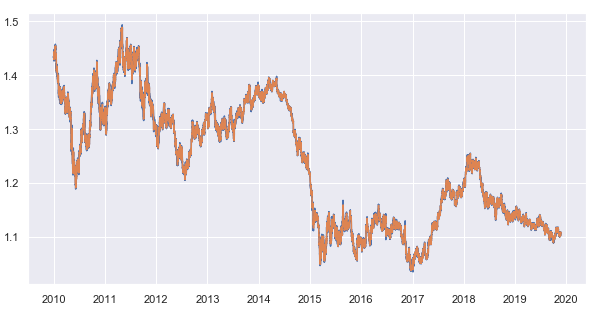
Fig. 7. Preços de fechamento do gráfico de 15 minutos e a média móvel de 25 períodos
Subtraímos a média móvel dos preços de fechamento e obtemos uma série temporal sem tendência (diferença):
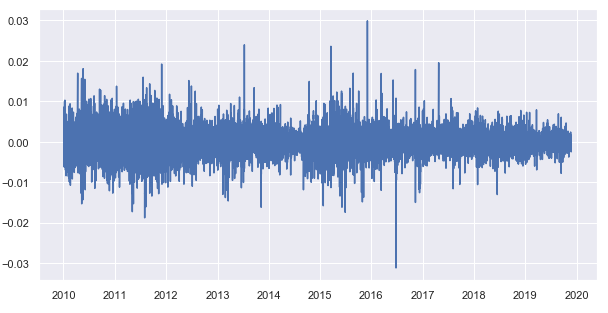
Fig. 8. Resultado da subtração da média móvel dos preços de fechamento
Agora vamos obter as estatísticas horárias da distribuição de sua diferença para cada hora de negociação:
Hourly_Returns = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(15, 8))
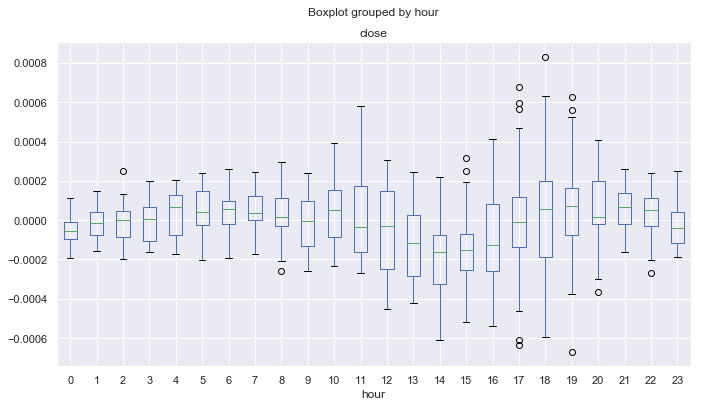
Fig. 9. Intervalo horário do incremento médio do preço dos últimos 10 anos, utilizando a MA de 25 períodos para eliminar a tendência no mês de novembro.
Diferentemente do diagrama da figura 6, criado para o incremento dos preços com um único atraso, esse diagrama mostra menos discrepâncias e revela padrões mais cíclicos. Por exemplo, você pode ver que das 0.00 até 08.00 (sessão do Pacífico) normalmente os preços estão subindo suavemente em relação à média móvel. Uma tendência de queda pode ser definida a partir das 12.00 até 14.00. Depois disso, durante a sessão nos EUA, os preços estão ascendentes em média. Após o início da sessão do Pacífico, os preços estão em declínio por 4 horas, a partir das 21.00.
O próximo passo lógico é examinar os momentos de distribuição para obter estimativas estatísticas mais precisas. Por exemplo, calcular o desvio padrão para as séries estacionárias resultantes como um diagrama do boxplot:
Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).std()
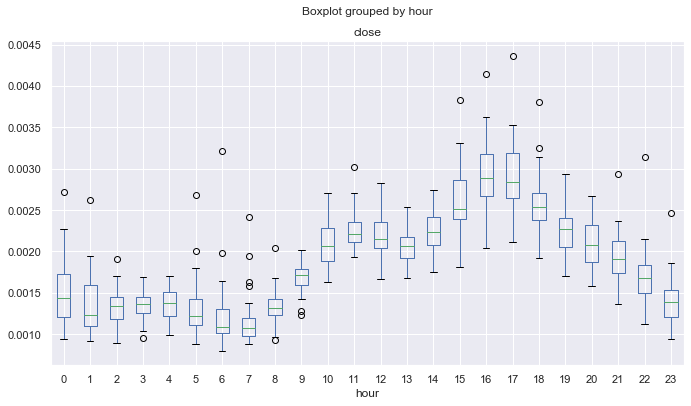
Fig. 10. Média dos desvios padrão do intervalo horário do incremento de preço dos últimos 10 anos, utilizando a MA de 25 períodos para eliminar a tendência.
A Fig. 10 mostra as horas com o comportamento de preço mais estável em termos do desvio padrão das expectativas matemáticas. Por exemplo, as horas 4, 13, 14, 19 têm uma dispersão estável em todos os dias e podem ser atraentes para as estratégias de reversão média. Outras horas podem ter valores discrepantes e o fio do bigode ser comprido, o que indica uma volatilidade mais variável em dias diferentes.
Outro ponto interessante é o coeficiente de assimetria. Vamos calculá-lo:
Hourly_skew = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).skew()

Fig. 11. Coeficientes médio de assimetria do incremento do preço por horas, em 10 anos, utilizando a MA de 25 períodos para eliminar a tendência.
A proximidade de zero e uma pequena dispersão indicam uma distribuição mais "padrão" dos incrementos. A forma do diagrama aqui se torna côncava. Por exemplo, embora as flutuações nas sessões européia e americana tenham maior dispersão (fig. 9), suas distribuições horárias são mais estáveis e menos tendenciosas, diferentemente das sessões do Pacífico e da Ásia. Isso pode resultar de grandes flutuações na atividade durante as duas últimas sessões, quando uma atividade de negociação quase nula é substituída por movimentos bruscos, que contribuem muito para o viés de distribuição.
A medida estatística de curtose mostra resultados semelhantes:
Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).apply(pd.DataFrame.kurt)
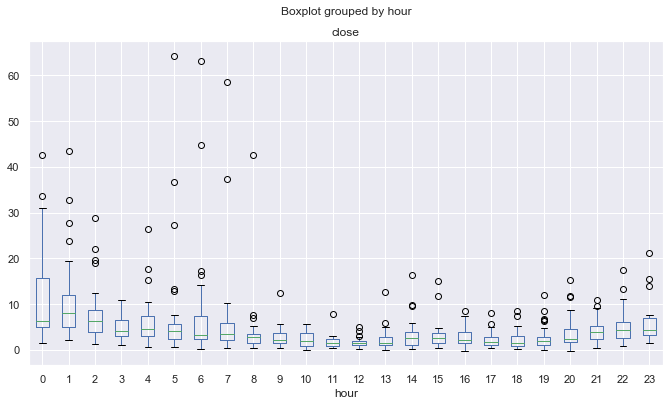
Fig. 12. Os coeficientes de curtose médios dos incrementos de preços por horas, em 10 anos, utilizando a MA de 25 períodos para eliminar a tendência.
Devido ao possível efeito mencionado acima, as distribuições são menos pontuais e mais "regulares" para as sessões de negociação mais voláteis e "irregulares" para as sessões de negociação mais calmas. Isso é um tipo de paradoxo.
Busca por padrões sazonais, utilizando uma MA para eliminar a tendência, para um mês ou dia específico da semana
Nós podemos visualizar a distribuição de preços por hora sem tendência para cada mês e dia da semana de maneira separada. O código inteiro está disponível nos anexos abaixo. Aqui, eu vou fornecer apenas a comparação entre março e novembro.
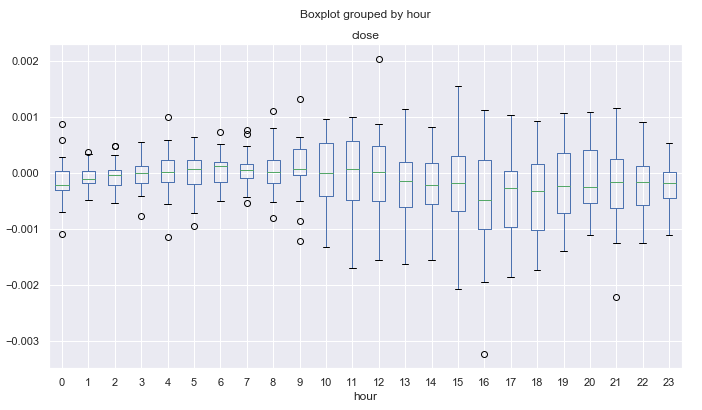
Fig. 13. Intervalo horário do incremento médio do preço dos últimos 10 anos, utilizando a MA de 25 períodos para eliminar a tendência no mês de março.
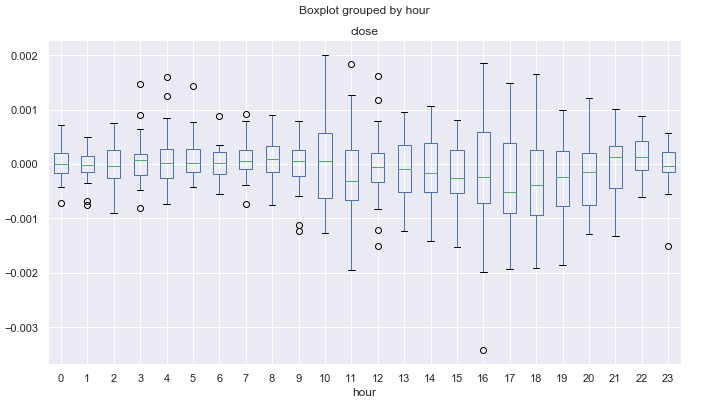
Fig. 14. Intervalo horário do incremento médio do preço dos últimos 10 anos, utilizando a MA de 25 períodos para eliminar a tendência no mês de novembro.
É possível buscar ciclos intradiários ainda menores, incluindo os dados de ticks, mas aqui nós lidamos apenas com os padrões sazonais básicos, que podem existir nas séries temporais financeiras, de acordo com a opinião dos traders. Você pode usar esses dados para desenvolver seus próprios sistemas de negociação, levando em consideração os recursos sazonais do instrumento financeiro.
Verificação dos padrões usando a lógica de negociação
Vamos criar um Expert Advisor de negociação simples, que utilizará os padrões encontrados mostrados na fig. 9. Mostra que de 0.00 a 04.00 (GMT+2), os preços em EURUSD aumentam em relação à sua média durante as quatro horas.
//+------------------------------------------------------------------+ //| Seasonal trader.mq5 | //| Copyright 2020, Max Dmitrievsky | //| https://www.mql5.com/en/users/dmitrievsky | //+------------------------------------------------------------------+ #property copyright "Copyright 2020, Max Dmitrievsky" #property link "https://www.mql5.com/en/users/dmitrievsky" #property version "1.00" #include <MT4Orders.mqh> #include <Trade\AccountInfo.mqh> #include <Math\Stat\Math.mqh> input int OrderMagic = 666; input double MaximumRisk=0.01; input double CustomLot=0; int hnd = iMA(NULL, 0, 25, 0, MODE_SMA, PRICE_CLOSE); MqlDateTime hours; double maArr[], prArr[]; void OnTick() { //--- CopyBuffer(hnd, 0, 0, 1, maArr); CopyClose(NULL, 0, 0, 1, prArr); double pr = prArr[0] - maArr[0]; TimeToStruct(TimeCurrent(), hours); if(hours.hour >=0 && hours.hour <=4) if(countOrders(0)==0 && countOrders(1)==0) if(pr < -0.0002) OrderSend(Symbol(),OP_BUY,0.01,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN); if(countOrders(0)!=0 && pr >=0) for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) { if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int countOrders(int a) { int result=0; for(int k=0; k<OrdersTotal(); k++) { if(OrderSelect(k,SELECT_BY_POS,MODE_TRADES)==true) if(OrderType()==a && OrderMagicNumber()==OrderMagic && OrderSymbol() == _Symbol) result++; } return(result); }
A média móvel usada é a mesma da estimativa estatística. Tem um período de 25. Subtraímos o valor médio do último preço conhecido e verificamos se o tempo de negociação atual está no intervalo de 0:00 a 4:00, inclusive. Como pode ser visto no diagrama na fig. 9, a diferença máxima entre o preço de fechamento e a média móvel nesse período é igual a -0.0002, enquanto a MA está acima de zero. Dessa forma, nossa lógica de negociação é abrir uma negociação de compra quando essa diferença for atingida e fechar a posição quando ela cair para zero. O robô de teste não possui ordens de stop ou outras verificações e destina-se apenas ao teste dos padrões encontrados. Executamos um teste de 2015 a 2019 no período gráfico de 15 minutos (a MA também foi construída nesse período em nosso estudo), no modo todos os ticks:
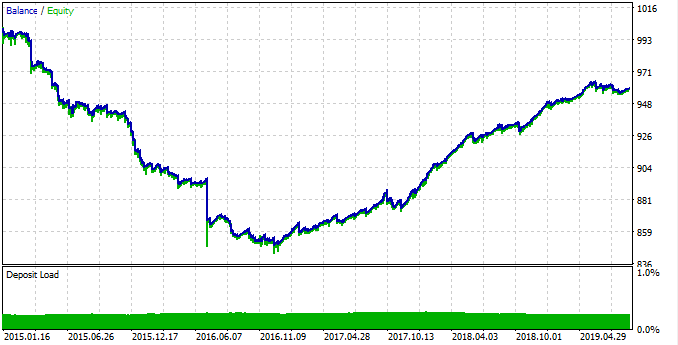
Fig. 15. Teste do padrão encontrado.
O padrão funcionou mal de 2015 a 2017 e o gráfico de lucro caiu. Então, um crescimento estável é mostrado de 2017 a 2019. Por que isso aconteceu? Para entendê-lo, vamos ver as estatísticas de cada intervalo de tempo separadamente.
Primeiro, aqui está o intervalo de negociação lucrativo:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2017, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
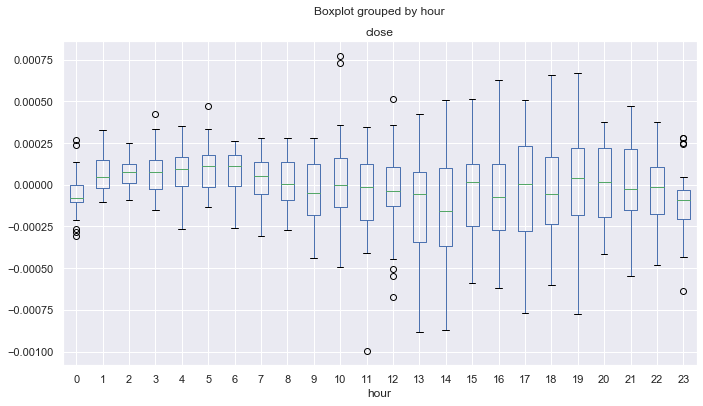
Fig. 16. Estatística dos anos 2017-2019.
Como podemos ver, a mediana de todas as horas (exceto zero) está acima de zero, em relação à média móvel. Desta maneira, alfa está estatisticamente do lado de nosso sistema de negociação, permanecendo com lucro em média. Agora, segue a distribuição para 2015-2017.
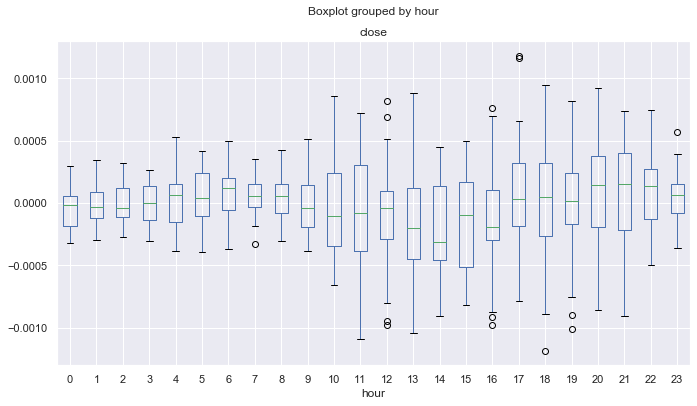
Fig. 17. Estatística dos anos 2015-2017.
Aqui, a mediana das distribuições é inferior ou igual a nulo para todas as horas, exceto a quarta, o que significa uma menor probabilidade para obtenção de lucro. Além disso, as caixas têm um intervalo médio significativamente maior em comparação com outro intervalo de tempo para o qual o valor mínimo não é inferior a -0.00025. Aqui está quase -0.0005. Outra desvantagem é a estimativa de distribuições apenas no preço de fechamento e, portanto, os picos de preços não são levados em consideração. Isso pode ser corrigido através da análise dos dados de tick, que estão além do escopo deste artigo. A diferença é clara e, portanto, você pode tentar ajustar o sistema para uniformizar os resultados de todos os anos.
Vamos permitir a abertura do negócio apenas nas horas 0-1. Assim, assumimos que nas próximas horas o negócio será fechado com lucro, porque o desvio médio tende a se mover em uma direção positiva. Além disso, vamos aumentar o limiar de fechamento do negócio de 0.0 para 0.0003 e, assim, o robô poderá obter maior lucro em potencial. As alterações são exibidas no código abaixo:
TimeToStruct(TimeCurrent(), hours); if(hours.hour >=0 && hours.hour <=1) if(countOrders(0)==0 && countOrders(1)==0) if(pr < -0.0004) OrderSend(Symbol(),OP_BUY,LotsOptimized(), SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN); if(countOrders(0)!=0 && pr >= 0.0003) for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) { if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; }
Vamos testar o robô para tirar uma conclusão final:
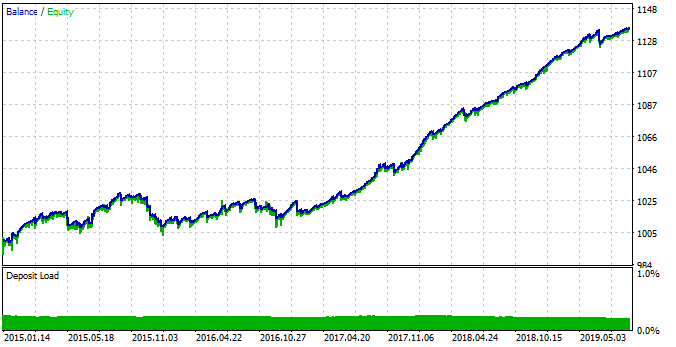
Fig. 18. Teste do padrão detectado com os parâmetros alterados do EA.
Desta vez, o sistema ficou mais estável no intervalo de tempo entre 2015 e 2017. No entanto, esse período não foi tão eficiente quanto o período entre 2017 e 2019, devido às mudanças nos padrões sazonais. Esse comportamento está relacionado a mudanças fundamentais no mercado, que podem ser facilmente descritas usando os diagramas boxplot.
Obviamente, ainda existem muitos padrões inexplorados, mas este exemplo básico fornece uma compreensão de novas possibilidades interessantes que se abrem ao usar essa técnica.
Conclusão
Este artigo apresenta uma descrição do método estatístico proposto para detectar padrões sazonais em séries temporais financeiras. O mercado pode ter ciclos mensais, bem como os ciclos intradiários, dependendo do mês. A análise horária mostrou que, com um determinado período de suavização (por exemplo, uma média móvel), é possível encontrar determinados ciclos dentro das sessões e ao passar de uma sessão de negociação para outra.
Uma das vantagens da abordagem é a possibilidade de trabalhar com padrões específicos de mercado sem a necessidade de otimização (ajuste excessivo de parâmetros) e, portanto, o sistema de negociação pode ser altamente estável.
Quanto às desvantagens, o processo de mineração de padrões sazonais não é fácil e envolve operações com várias combinações e ciclos.
A análise foi realizada para o par de moedas EURUSD, com o intervalo de 10 anos. Os códigos fonte em Python estão anexados no final do artigo no formato .ipynb (Jupyter notebook). Você pode executar o mesmo estudo para qualquer instrumento financeiro desejado, usando a biblioteca em anexo, e aplicar os resultados obtidos para criar seu próprio sistema de negociação ou aprimorar algum já existente.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/7038
 Ampliando as funcionalidades do Construtor de Estratégia
Ampliando as funcionalidades do Construtor de Estratégia
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso