MetaTrader 5
Experts
지표
스크립트
라이브러리
보관함당사 팬 페이지에 가입하십시오
- 조회수:
- 437
- 평가:
- 게시됨:
- 2021.11.25 15:29
-
이 코드를 기반으로 한 로봇이나 지표가 필요하신가요? 프리랜스로 주문하세요
프리랜스로 이동
Fractal Adaptive Moving Average 기술적 지표(FRAMA)는 John Ehlers에 의해 개발되었습니다.
이 지표는 알고리즘을 기반으로 구성됩니다.지수 이동 평균, 평활 계수는 가격 계열의 현재 프랙탈 차원을 기반으로 계산됩니다. FRAMA의 장점은 강한 추세의 움직임을 따라갈 수 있고 가격이 수렴할 때 충분히 기다릴 수 있다는 것입니다.
이동 평균에 사용되는 모든 분석 방법이 이 지표에도 적용될 수 있습니다.
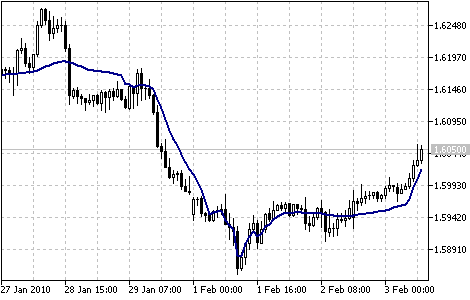
Fractal Adaptive Moving Average 지표
계산:
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
설명:
- FRAMA(i) - FRAMA의 현재 값;
- Price(i) - 현재 가;
- FRAMA(i-1) - FRAMA의 이전 값;
- A(i) - 지수 평활화의 현재 계수.
지수 평활 계수는 아래 공식에 따라 계산됩니다.
A(i) = EXP(-4.6 * (D(i) - 1))
설명:
- D(i) - 현재 프랙탈 차원;
- EXP() - 지수의 수학 함수.
직선의 프랙탈 차원은 1과 같습니다. 공식에서 D = 1이면 A = EXP(-4.6 *(1-1)) = EXP(0) = 1임을 알 수 있습니다. 따라서 가격이 직선으로 변경되면 지수 평활이 사용되지 않습니다. 이러한 경우 공식은 다음과 같기 때문입니다.
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
즉, 지표는 가격을 정확히 따릅니다.
평면의 프랙탈 차원은 2와 같습니다. 공식에서 D = 2이면 평활 계수 A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01입니다. 지수 평활 계수의 이러한 작은 값은 가격이 강한 움직임을 만드는 순간에 얻어집니다. 이러한 강한 둔화는 약 200주기의 단순 이동 평균에 해당합니다.
프랙탈 차원의 공식:
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
추가 공식에 따라 계산됩니다.
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
설명:
- HighestPrice(i) - Length 기간에 대한 현재 최대값;
- LowestPrice(i) - Length 기간에 대한 현재 최저값;
값 N1, N2 및 N3은 각각 다음과 같습니다.
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
MetaQuotes Ltd에서 영어로 번역함.
원본 코드: https://www.mql5.com/en/code/72
ObjChartSample
이 스크립트는 표준 라이브러리(CChart)의 클래스를 사용하여 차트 속성을 제어하는 방법을 보여줍니다.
스피어샘플(SphereSample)
이 스크립트는 표준 라이브러리의 클래스를 사용하여 그래픽 객체를 제어하는 방법을 보여줍니다.
더블 지수 이동 평균(Double Exponential Moving Average (DEMA))
지표는 가격 계열을 평활화 하는 데 사용되며 금융 유가 증권의 가격 차트에 직접 적용됩니다.
Average Directional Movement Index Wilder
와일더의 Average Directional Movement Index(ADX Wilder)는 가격의 추세가 있는지를 확인하는데 도움이 됩니다.