MetaTrader 5
Experts
Indicadores
Scripts
Bibliotecas
RepositórioParticipe de nossa página de fãs
Coloque um link para ele, e permita que outras pessoas também o avaliem
Avalie seu funcionamento no terminal MetaTrader 5
- Visualizações:
- 5090
- Avaliação:
- Publicado:
- 2014.01.14 14:43
- Atualizado:
- 2016.11.22 07:33
-
Você está perdendo oportunidades de negociação:- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro LoginVocê concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
-
Precisa de um robô ou indicador baseado nesse código? Solicite-o no Freelance
Ir para Freelance
O indicador técnico Fractal Adaptive Moving Average (FRAMA) foi desenvolvido por John Ehlers.
Este indicador é construído baseado no algoritmo de Exponential Moving Average, em que o fator de suavização é calculado com base na dimensão fractal atual da série preço. A vantagem de FRAMA é a possibilidade de seguir movimentos de tendências fortes e desacelerar nos momentos de consolidação de preços.
Todos os tipos de análise utilizados em Moving Averages podem ser aplicados a este indicador.
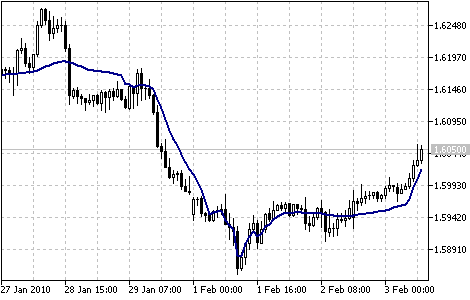
Indicador Fractal Adaptive Moving Average
Cálculo:
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
onde:
- FRAMA(i) - valor atual de FRAMA;
- Price(i) - preço atual;
- FRAMA(i-1) - valor anterior de FRAMA;
- A(i) - fator atual de suavização exponencial.
O fator de suavização exponencial é calculado de acordo com a fórmula abaixo:
A(i) = EXP(-4.6 * (D(i) - 1))
onde:
- D(i) - dimensão fractal atual;
- EXP() - função matemática de expoente.
A dimensão fractal de uma linha reta é igual a um. Vê-se a partir da fórmula que se D = 1, então A = EXP(-4.6 *(1-1)) = EXP(0) = 1. Assim, se o preço muda em linhas reta, a suavização exponencial não é usada, pois em tal caso a fórmula seria assim:
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
Ou seja, o indicador segue exatamente o preço.
A dimensão fractal de um plano é igual a dois. Vê-se a partir da fórmula que se D = 2, então o fator de suavização A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01. Esse pequeno valor do fator de ponderação exponencial é obtido em momentos quando o preço faz um forte movimento de serra dentilhada. Tal forte desaceleração corresponde a aproximadamente um período de 200 em uma simple moving average.
Fórmula da dimensão fractal:
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
Ele é calculado com base na fórmula adicional:
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
onde:
- HighestPrice(i) - valor máximo atual para os períodos;
- LowestPrice(i) - valor mínimo atual para os períodos;
Os valores N1, N2 e N3 são respectivamente iguais a:
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
Traduzido do inglês pela MetaQuotes Ltd.
Publicação original: https://www.mql5.com/en/code/72
Double Exponential Moving Average (DEMA)
Ele é usado para suavizar uma série de preços e é aplicado diretamente sobre uma tabela de preços de uma instrumento financeiro.
Triple Exponential Moving Average (TEMA)
TEMA pode ser usado no lugar de moving averages tradicionais. Ele pode ser usado para suavizar os dados de preço, bem como para suavizar outros indicadores.
TradePad_Sample
Este é um exemplo simples, do sistema de informação, com a possibilidade de negociar pressionando um botão.
ObjChartSample
O script ilustra o controle de propriedades do gráfico usando as classes da biblioteca padrão (CChart).