MetaTrader 5
EA
指标
脚本
程序库
存储- 显示:
- 4953
- 等级:
- 已发布:
- 2013.10.01 12:29
- 已更新:
- 2016.11.22 07:33
-
需要基于此代码的EA交易或指标吗？请在自由职业者服务中订购
进入自由职业者服务
分形自适应移动平均线 技术指标 (FRAMA) 由John Ehlers开发。
这个指标基于指数移动平均线算法构建, 其中平滑因子是基于当前价格序列的分形维数计算的。FRAMA的优点是能跟随强趋势运动并能在价格合并时刻突然减缓。
用于移动平均线的各种类型分析都可以应用到这个指标。
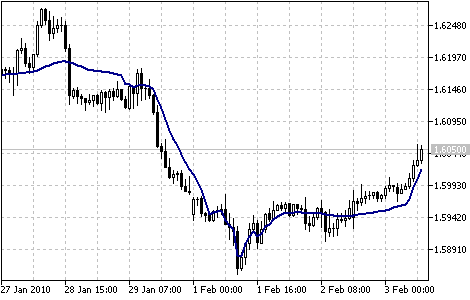
分形自适应移动平均线指标
计算公式：
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
其中：
- FRAMA(i) - FRAMA的当前值；
- Price(i) - 当前价格；
- FRAMA(i-1) - FRAMA的先前值；
- A(i) - 当前指数平滑因子。
指数平滑因子根据下面的公式进行计算：
A(i) = EXP(-4.6 * (D(i) - 1))
其中：
- D(i) - 当前的分形维数；
- EXP() - 指数的数学函数。
直线的分形维数等于一。从公式可见，如果 D = 1, 那么 A = EXP(-4.6 *(1-1)) = EXP(0) = 1。因此，如果价格以直线变动，指数平滑则没有使用，因为在这种情况下，公式则像这样的：
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
即指标完全遵循价格。
一个平面的分形维数等于二。从公式可得到：如果D =2，那么平滑因子A= EXP（-4.6*（2-1））= EXP（-4.6）= 0.01。. 指数平滑因子的一个这样的小数值，可在价格出现强烈的锯齿形运动时得到。这种强烈的放缓对应于约200周期的简单移动平均线。
分形维数的公式：
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
它的计算基于另一个公式：
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
其中：
- HighestPrice(i) - 长周期的当前最大值；
- LowestPrice(i) - 长周期的当前最小值；
N1，N2和N3的值分别等于：
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
由MetaQuotes Ltd译自英文
原代码： https://www.mql5.com/en/code/72
Double Exponential Moving Average (DEMA)
它被用于平滑价格序列并且被直接应用在金融资产的价格图表上。
三重指数移动平均线(TEMA)
TEMA可以用来替代传统移动平均线。它也可以用来平滑价格数据，以及平滑其他指标。