Algoritmo di riacquisto: Modello matematico per aumentare l'efficienza

Contenuto

• Introduzione
• Metodi di affinamento delle caratteristiche di trading basati sull'algoritmo di mediazione
• "Aiutatemi ad uscire dal drawdown".
• Considerazioni generali sull'algoritmo di mediazione
• Le sottigliezze di una valutazione più accurata dei sistemi di riacquisto
• Comprensione approfondita e universale della profittabilità
• Valutazione universale
• Esempi di metodi chiarificatori
• Aumentare l'efficienza dei sistemi con la diversificazione
• Limiti utili
• Caratteristiche utili per l'utilizzo di strumenti paralleli
• Distribuzione normale di una variabile casuale
• Bellezza della curva di profitto nel quadro della legge di distribuzione dei valori casuali
• Conclusioni

Introduzione

Questo metodo di trading viene utilizzato attivamente in un'ampia varietà di Expert Advisor. Peraltro, presenta numerose varianti e ibridi. Inoltre, a giudicare dal numero di riferimenti a tali sistemi, è evidente che questo argomento è molto popolare non solo su questo sito, ma anche su qualsiasi altra risorsa web. Tutte le varianti del metodo hanno in comune il concetto di trading contro il movimento del mercato. In altre parole, l'EA utilizza i riacquisti per poter acquistare il più basso possibile e vendere il più alto possibile.

Si tratta di un classico schema di trading vecchio come il mondo. In uno degli articoli precedenti, ho toccato parzialmente questo argomento, evidenziando i possibili modi per ibridare tali metodi. In questo articolo, daremo un'occhiata più da vicino a questo concetto, approfondendo la questione rispetto a quanto fanno gli utenti dei forum. Tuttavia, l'articolo sarà più generale e molto più ampio, poiché l'algoritmo di riacquisto è molto adatto a mettere in evidenza alcune caratteristiche molto interessanti e utili.

Metodi di affinamento delle caratteristiche di trading basati sull'algoritmo di mediazione

"Aiutatemi ad uscire dal drawdown" (dagli autori di "il mio EA guadagna bene, ma a volte fa saltare l'intero conto")

Si tratta di un problema comune a molti trader algoritmici e manuali. Al momento di scrivere questo articolo, ho avuto una conversazione con una persona di questo tipo, ma non ha colto il mio punto di vista nella sua interezza. Purtroppo, mi sembra che non abbia praticamente nessuna possibilità di capire l’intera commedia di una situazione del genere. Dopo tutto, se potessi porre una domanda simile al mio io più anziano e più esperto, molto probabilmente non riuscirei a capire la risposta. So anche come mi farebbero sentire, le risposte vere al me stesso. Penserei di essere umiliato o di essere dissuaso dall'impegnarmi ulteriormente nel trading algoritmico.

In realtà, tutto è molto più semplice. Ho solo avuto la pazienza di percorrere un certo sentiero e di acquisire una certa saggezza, se così si può dire. Non si tratta di un'idealizzazione e di un'auto-elogio, ma piuttosto, di un minimo indispensabile. È un peccato che questo percorso abbia richiesto anni invece di settimane e mesi.

Qui c'è un intero mondo di sogni e di autoinganni e ad essere onesti, sto già iniziando a stancarmi della semplicità di alcune persone. Per favore, smettetela di fare sciocchezze e di pensare di essere i re del mercato. Contattate invece una persona esperta e chiedetele di scegliere un EA adatto al vostro budget. Credetemi, in questo modo risparmierete molto tempo e denaro, per non parlare della vostra sanità mentale. Una di queste persone ha scritto questo articolo. Le prove sono riportate di seguito.

Considerazioni generali sull'algoritmo di mediazione

Se diamo un'occhiata all'algoritmo di riacquisto o "mediazione", potrebbe sembrare che questo sistema non abbia alcun rischio di perdita. C'è stato un tempo quando non sapevo ancora nulla di questi trucchi e mi sorprendevo delle enormi aspettative matematiche che battevano qualsiasi spread. Ora è chiaro che si tratta solo di un'illusione, tuttavia c'è una venatura razionale in questo approccio, ma ne parleremo più avanti. Innanzitutto, per poter valutare oggettivamente tali sistemi, è necessario conoscere alcuni parametri indiretti che possano dirci qualcosa di più di una semplice immagine di crescita dei profitti.

I parametri più rilevanti del report del tester di strategia possono persino aiutare a capire che il sistema sta ovviamente perdendo, nonostante la curva del saldo sembri ottima. Come avrete già capito, si tratta della curva di profittabilità. In effetti, tutti gli indicatori importanti del sistema di trading sono secondari rispetto alle prime e più basilari caratteristiche matematiche, che, ovviamente, sono l'aspettativa matematica e le sue caratteristiche primarie. Ma vale la pena notare che l'aspettativa matematica è un valore così flessibile che si può sempre cadere nella trappola dell’illusione.

Infatti, per utilizzare correttamente un concetto come quello di aspettativa matematica, bisogna innanzitutto capire che si tratta della terminologia della teoria della probabilità e che qualsiasi calcolo di questa grandezza deve essere effettuato secondo le regole della teoria della probabilità, ossia:

• I calcoli sono tanto più accurati quanto più grande è il campione analizzato; idealmente il valore esatto viene calcolato da un campione infinito.
• Se scomponiamo l'infinito in più parti, otteniamo diversi infiniti

Qualcuno potrebbe pensare a come calcolare l'esatta aspettativa matematica di una particolare strategia, se abbiamo a disposizione solo un campione limitato di quotazioni reali. E qualcun’altro penserà: perché abbiamo bisogno di questi infiniti? Il fatto è che tutte le stime di certi valori medi, come le aspettative matematiche, hanno peso solo nell'area in cui questi calcoli sono stati fatti, ma non hanno nulla a che fare con un'altra area. Qualsiasi caratteristica matematica ha peso solo dove viene calcolata. Tuttavia, si possono distinguere alcune tecniche per affinare le caratteristiche della profittabilità di una particolare strategia, che consentiranno di ottenere i valori più vicini a quelli reali dei parametri richiesti.

Questo è direttamente collegato al nostro compito. Dopo aver capito che non possiamo vedere il futuro di una strategia infinita, che di per sé suona già come un'assurdità. Tuttavia, questo è un fatto matematico e una condizione necessaria e sufficiente per calcolare le vere caratteristiche matematiche. Veniamo all'idea di come rendere il numero calcolato su un campione limitato più vicino al numero che potrebbe essere calcolato su un campione infinito. Chi ha familiarità con la matematica sa che esistono due concetti matematici che possono essere applicati per calcolare somme infinite:

• Integrali
• Somma di serie infinite

Credo sia chiaro a tutti che per calcolare l'integrale, così come la somma delle serie, è necessario ottenere o tutti i punti della funzione di cui si vuole calcolare l'integrale, all'interno dell'area di integrazione considerata, oppure tutti gli elementi della sequenza di numeri all'interno della serie considerata. C'è ancora l'opzione perfetta: ottenere le espressioni matematiche appropriate per la funzione che si intende integrare e l'espressione per generare gli elementi della serie. In molti casi, se disponiamo delle espressioni matematiche appropriate, possiamo ottenere le equazioni esatte per l'integrale finito o la somma delle serie, ma nel caso del trading reale non potremo applicare il calcolo differenziale e in generale questo non ci aiuterà molto, ma è importante capirlo.

La conclusione di tutto ciò è che per la valutazione diretta di qualsiasi sistema disponiamo solo di un campione limitato e di alcuni parametri che otteniamo nello strategy tester. In realtà, la loro importanza è molto esagerata. Ci si chiede se sia possibile giudicare la profittabilità di una particolare strategia utilizzando i parametri dello Strategy Tester, se questi parametri siano sufficienti per una risposta univoca e, soprattutto, come utilizzare correttamente questi parametri e se li utilizziamo davvero correttamente.

Inoltre, dobbiamo capire che per ogni strategia, qualsiasi parametro, in base al quale possiamo valutare correttamente la reale profittabilità e sicurezza della strategia, può essere completamente differente. Ciò è direttamente collegato alla valutazione della curva dei profitti. Per capirlo, tracciamo innanzitutto una visione generale approssimativa della curva di trading che si ottiene utilizzando l'algoritmo di riacquisto:

Fig. 1

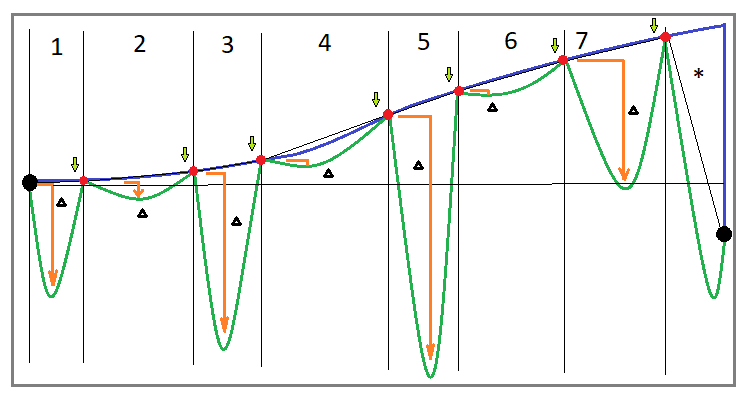
Cominciamo con l'implementazione di un riacquisto per uno strumento. Se implementate correttamente questo algoritmo, il vostro trading sarà in ogni caso composto da cicli. Idealmente, tutti i cicli dovrebbero essere positivi. Se alcuni cicli si chiudono nella zona negativa, allora o l'algoritmo è implementato in modo errato, oppure non è più un algoritmo puro e ha già subito delle modifiche. Ma considereremo il riacquisto classico. Definiamo alcuni parametri caratteristici della curva di trading per indicare un classico riacquisto:

• La curva del saldo deve essere crescente e consistere di N cicli
• Tutti i cicli hanno un profitto positivo
• Quando il trading si interrompe, è probabile che ci si trovi nell'ultimo ciclo incompleto
• Il ciclo incompleto ha una profittabilità negativa
• I cicli hanno un caratteristico drawdown in termini di fondi.

Sembra che l'aspetto generale della curva dovrebbe rendere chiaro a prima vista che questo sistema è redditizio, ma non tutto è così semplice. Se osservate l'ultimo ciclo di trading non concluso, che ho chiuso specificamente al di sotto del punto di partenza, vedrete che in alcuni casi sarete fortunati e aspetterete per il successo del completamento del ciclo, mentre in altri casi potreste non aspettare fino alla fine e affrontare una grossa perdita o mandare all'aria il vostro intero deposito. Perché succede? Il fatto è che l'immagine può dare la falsa impressione che l'importo del drawdown dei fondi sia limitato nel suo valore assoluto e, di conseguenza, anche il tempo trascorso in questo drawdown dovrebbe essere limitato.

In realtà, più lunga è l'area di test, più lunga è l'area di drawdown medio. Non c'è assolutamente alcun limite. Il limite esiste solo nella forma del vostro deposito e nella qualità della vostra gestione del denaro. Tuttavia, un approccio competente all'impostazione del sistema, basato su questo principio, può solo portare ad un aumento della durata del deposito prima che questo venga fatto saltare o, nel migliore dei casi, produrre un profitto molto limitato.

Quando si tratta di testare i sistemi basati sull'algoritmo di riacquisto (mediazione), per valutarne correttamente la sopravvivenza, l'affidabilità e la reale profittabilità, è necessario attenersi ad una struttura di test speciale. Il punto è che il valore di un singolo test in questo approccio è ridotto al minimo per una semplice ragione: quando si testa una qualsiasi strategia "normale", il profitto per l'intero test nel tester della strategia è molto vicino al valore "normalmente" distribuito. Ciò significa che quando si testa una qualsiasi strategia di mediazione senza mantenere una posizione per un lungo periodo di tempo, si otterrà un numero approssimativamente uguale di aree di test redditizie e non redditizie, il che vi farà capire molto rapidamente che la strategia è instabile, oppure che la strategia ha una corretta comprensione del mercato e funziona sull'intera storia.

Quando si tratta con una strategia di riacquisto, questa distribuzione può essere fortemente deformata, perché per testare correttamente questo sistema è necessario impostare il massimo deposito possibile. Inoltre, il risultato del test dipende fortemente dalla lunghezza della sezione di prova. In effetti, in questo approccio, tutto il trading si basa su cicli di trading ed ogni singola impostazione di questo sistema può avere sia un parametro completamente diverso del drawdown medio sia il parametro della durata media del drawdown ad esso associato. A seconda di questi indicatori, sezioni di test troppo brevi possono mostrare risultati troppo alti o troppo bassi. Di norma, sono pochi i test di questo tipo che vengono eseguiti e questo può essere, nella maggior parte dei casi, la causa di un'eccessiva fiducia nel funzionamento di questi sistemi.

Le sottigliezze di una valutazione più accurata dei sistemi di riacquisto

Ora impariamo come valutare correttamente le prestazioni dei sistemi che utilizzano l'algoritmo di riacquisto, applicando i parametri noti dei sistemi di trading. Innanzitutto, per una valutazione di questo tipo, consiglierei di utilizzare un'unica caratteristica - il fattore di recupero. Cerchiamo di capire come calcolarlo:

• Fattore di recupero = Profitto Totale / Massimo Drawdown del Capitale Netto
• Profitto totale - profitto totale per area di trading
  
• Massimo Drawdown del Capitale Netto - massimo drawdown del capitale relativo al precedente punto di congiunzione per il saldo e il capitale netto (picco del saldo)
  

Come si vede, si tratta del profitto finale diviso per il massimo drawdown dei fondi. Il significato matematico di questo indicatore in senso classico è che, secondo l'idea, dovrebbe mostrare la capacità del sistema di ripristinare il proprio drawdown tramite il capitale netto (equity). La condizione di base per la redditività di un sistema di trading quando si utilizza tale caratteristica è il seguente fatto:

• Fattore di recupero > 1
  

Se tradotto in un linguaggio umano comprensibile, significherebbe che per ottenere un profitto non possiamo rischiare più dello stesso importo del deposito. Questo parametro in molti casi fornisce una valutazione accurata della qualità del trading per un particolare sistema. Utilizzatelo, ma fate molta attenzione, perché si tratta di un valore piuttosto controverso per quanto riguarda il suo significato matematico.

Tuttavia, dovrò rivelarvi tutti i suoi svantaggi, in modo da farvi capire che anche questo parametro è molto arbitrario e il livello del suo significato matematico è molto basso. Naturalmente, si potrebbe dire che se si critica qualcosa, si deve offrire un'alternativa. Lo farò sicuramente, ma solo dopo aver analizzato questo parametro. Questo parametro è legato al drawdown massimo, che a sua volta può essere legato a qualsiasi punto della curva di trading, il che significa che se ricalcoliamo questo drawdown rispetto al saldo iniziale e lo sostituiamo al drawdown massimo, otteniamo quasi sempre un fattore di recupero sovrastimato. Formalizziamo il tutto in modo corretto:

• Fattore di Recupero Variante 1 = Profitto Totale / Massimo Drawdown di Capitale Netto dall'Inizio
• Massimo Drawdown di Capitale Netto dall'Inizio - massimo drawdown del saldo iniziale (non dal massimo precedente)
  

Naturalmente non si tratta di un fattore di recupero classico, ma nella sua essenza determina effettivamente la profittabilità in modo molto più corretto rispetto alla condizione limite generalmente accettata. Descriviamo prima visivamente entrambe le opzioni per il calcolo di questo indicatore - quello classico e il mio: 

Fig. 2

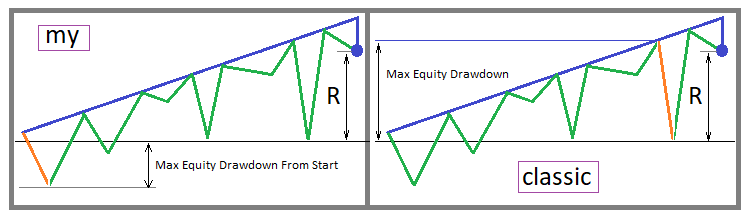
Si può notare che nel primo caso, questo parametro assumerà valori più alti, il che, ovviamente, è ciò che vogliamo. Ma dal punto di vista della valutazione della profittabilità, si possono seguire due approcci. Il parametro classico è più adatto all'approccio, in cui è meglio prendere la durata della sezione di prova il più lunga possibile. In questo caso, un valore più alto del Massimo Drawdown del Capitale Netto compensa il fatto che questo drawdown non inizia fin dall'inizio della curva di trading, e quindi questo parametro nella maggior parte dei casi si avvicina alla stima reale. Il mio parametro è più efficiente quando si valutano più backtest.

In altre parole, questo parametro è tanto più preciso quanto maggiore è il numero di test effettuati sulla strategia. I test della vostra strategia devono riguardare il maggior numero possibile di aree differenti. Ciò significa che i punti di inizio e fine devono essere scelti con la massima variabilità. Per una corretta valutazione, è necessario selezionare "N" aree tra le più diverse e sottoporle a test, per poi calcolare la media aritmetica di questo indicatore per tutte le aree di test. Questa regola ci consentirà di perfezionare entrambe le versioni del fattore di recupero, sia la mia che quella classica, con l'unica modifica che per perfezionare quella classica sarà necessario eseguire un minor numero di backtest indipendenti.

Tuttavia, dire che tali manipolazioni chiarificatrici sono poche per chiarire questi parametri sarebbe un eufemismo. Ho mostrato la mia versione del fattore di recupero per dimostrare che chiunque può creare un proprio parametro simile, che può anche essere aggiunto come una delle caratteristiche calcolate per il backtest in MetaTrader. Ma ognuno di questi parametri non ha alcuna prova matematica e, inoltre, ognuno di questi parametri ha i propri errori e limiti di applicabilità. Tutto ciò significa che al momento non esiste un indicatore matematico esatto per una valutazione assolutamente accurata di uno o dell'altro algoritmo che utilizza il riacquisto. Tuttavia, il mio parametro tenderà alla precisione assoluta con un aumento nel numero di test. Fornirò maggiori dettagli nella prossima sezione.

Comprensione approfondita e universale della profittabilità

Valutazione universale

Credo che tutti sappiano che parametri come l'aspettativa matematica del profitto e il fattore di profitto sono presenti in qualsiasi rapporto di un tester di strategia o nelle caratteristiche di un segnale di trading, ma credo che nessuno vi abbia detto che queste caratteristiche possono essere utilizzate anche per calcolare la profittabilità di tali sistemi di trading in cui non c'è un'analisi sufficiente delle operazioni. È quindi possibile utilizzare questi parametri sostituendo l'unità "posizione" con "test sul segmento". Quando si calcola questo indicatore, è necessario effettuare molti test indipendenti senza tenere conto di alcuna struttura interna. Questo approccio vi aiuterà a valutare le reali prospettive del sistema di trading utilizzando solo i due parametri più popolari. Inoltre, può instillare in voi un'abitudine estremamente utile - i test multipli. Per utilizzare questo approccio, è sufficiente conoscere la seguente equazione:

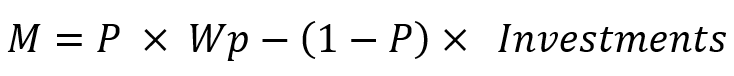
dove:

• M - valore di payoff atteso
• Wp - profitto desiderato
• Investments - quanto si è disposti a investire per ottenere il profitto desiderato.
• P - probabilità di avere investimenti sufficienti fino al raggiungimento del profitto
• (1-P) - probabilità di non avere un investimento sufficiente fino al raggiungimento del profitto (perdita del deposito)

Di seguito è riportata un'equazione simile per il fattore di profitto:

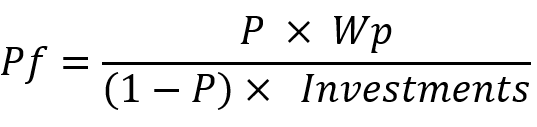
Tutto ciò che dovete sapere è che con il trading casuale e l'assenza di ostacoli quali spread, commissioni e swap, nonché lo slippage, queste variabili assumeranno sempre i seguenti valori per qualsiasi sistema di trading:

M=0

Pf=1

Queste caratteristiche possono cambiare nella vostra direzione solo se c'è un momento di previsione. Pertanto, la probabilità di ottenere un profitto senza perdere il deposito assumerà il seguente valore:

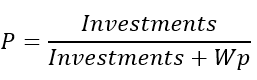
Se si sostituisce questa espressione alla probabilità nelle nostre equazioni, allora otterremo l'identità che ho fornito. Se consideriamo spread, commissioni e swap, otteniamo quanto segue:

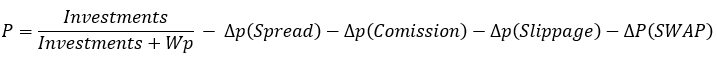
Lo spread, la commissione e lo swap riducono la probabilità finale, il che fa sì che le identità perdano la loro validità. Invece, si riscontrano le seguenti disparità:

• M < 0
• Pf < 1

Questo accade con qualsiasi sistema di trading e l’algoritmo di riacquisto non è assolutamente migliore di qualsiasi altro sistema. Quando si testa o si opera con un sistema di questo tipo, esso è in grado di deformare fortemente la funzione di distribuzione del valore casuale del segnale o del profitto finale del backtest, ma in genere questo scenario si verifica più frequentemente durante i test o il funzionamento a breve termine.

Questo perché la probabilità di incappare in un forte drawdown è molto minore se si effettua il test su una sezione corta. Ma quando si iniziano a fare questi test su segmenti più lunghi, di solito si vedono cose che non si erano mai viste prima. Ma sono sicuro che la maggior parte sarà in grado di rassicurarsi sul fatto che si tratta solo di un incidente e che è sufficiente aggirare in qualche modo queste aree pericolose. Lo stesso vale in genere per i test multipli su segmenti corti.

C'è un solo modo per superare la non redditività di qualsiasi sistema. Aggiungiamo un ulteriore componente all'equazione del calcolo delle probabilità:

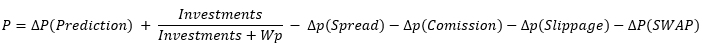
Come si può notare, nell'equazione è comparsa la nuova componente "dP(Prediction)". Ha un segno più, fatto apposta per mostrare che solo questo componente è in grado di compensare l'effetto di spread, commissioni e swap. Ciò significa che abbiamo bisogno innanzitutto di una qualità di previsione sufficiente per superare gli effetti negativi e raggiungere il profitto:

Possiamo ottenere le disuguaglianze desiderate solo se forniamo questa particolare disuguaglianza:

• M > 0
• Pf > 1

Come potete vedere, queste espressioni sono molto facili da capire e sono sicuro che nessuno dubiterà della loro correttezza. La prossima sottosezione sarà più facile da capire utilizzando queste equazioni. Anzi, vi consiglio di ricordarle, o almeno di ricordarne la logica, in modo da poterle sempre ripristinare in memoria se necessario. L'aspetto principale qui è la loro comprensione. In generale, una di queste equazioni è sufficiente, ma ho pensato che sarebbe stato meglio mostrarne due a titolo di esempio. Per quanto riguarda gli altri parametri, credo che siano superflui nell'ambito di questa sezione.

Esempi di metodi chiarificatori

In questa sottosezione, vi proporrò alcune manipolazioni di rifinitura aggiuntive che vi permetteranno di ottenere un valore più corretto del fattore di recupero. Suggerisco di tornare alla "Figura 1" e di osservare i segmenti numerati. Per affinare il fattore di recupero, è necessario immaginare che questi segmenti siano test indipendenti. In questo modo possiamo fare a meno di effettuare test multipli, supponendo di averli già eseguiti. Possiamo farlo perché questi segmenti sono cicli che hanno sia un punto di inizio che un punto di fine, il che è ciò che fornisce l'equivalenza con il backtest. 

Nell'ambito di questa sezione, credo che valga la pena di integrare la prima immagine con un'immagine equivalente, considerando il fatto che stiamo testando o facendo trading su diversi strumenti contemporaneamente. Ecco come apparirà la curva di trading utilizzando l'algoritmo di riacquisto per il trading parallelo su più strumenti:

Fig. 3

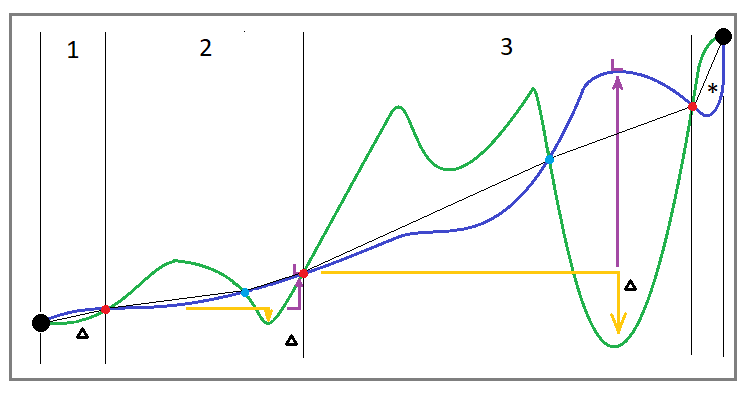
Possiamo notare che questa curva differisce nella sua struttura dalla curva di riacquisto su uno strumento. Qui ho aggiunto dei punti blu intermedi, il che significa che prima del drawdown potrebbero esserci dei segmenti che presentano un "drawdown al contrario". Il fatto è che non possiamo considerarlo un drawdown. Tuttavia, non abbiamo il diritto di considerare questi segmenti al di fuori dell'analisi. Per questo motivo devono far parte di un ciclo.

Credo che sarebbe più corretto posticipare ogni nuovo ciclo alla fine del precedente. In questo caso, la fine del ciclo precedente dovrebbe essere considerato il punto di recupero dell'ultimo drawdown dell'equity. Nell'immagine, questi cicli sono separati da punti rossi. Ma in realtà questa definizione del ciclo non è sufficiente. È inoltre importante stabilire che non è sufficiente fissare solo il drawdown con l'equity, ma è importante che sia inferiore all'inizio del ciclo attuale. Altrimenti, che tipo di drawdown è?

Dopo aver evidenziato questi cicli, è possibile considerarli come test indipendenti separati e calcolare il fattore di recupero per ognuno di loro. Questo può essere fatto nel modo seguente:

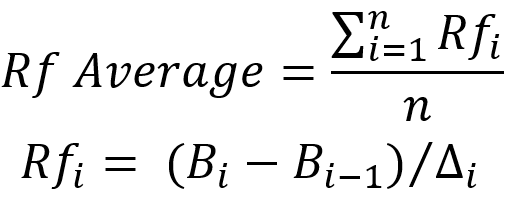
In questa equazione, i punti corrispondenti sulla curva del saldo (il valore finale del saldo sulla sezione e quello iniziale) sono utilizzati come "B", mentre il delta rappresenta il nostro drawdown. Vorrei anche che il lettore tornasse all'ultima immagine. Sull’immagine, ho tracciato il delta dal punto di partenza rosso di ciascun ciclo e non da quello blu, come avviene di solito, per i motivi che ho elencato sopra. Ma se ti è necessario chiarire il fattore di recupero originale, il delta deve essere tracciato dal punto blu. In questo caso, il metodo di affinamento dei parametri è più importante dei parametri stessi. La media aritmetica semplice viene presa come azione di mediazione.

Tuttavia, anche dopo aver chiarito l'uno o l'altro parametro personalizzato o classico, non si deve considerare il fatto che il valore di questo indicatore sia superiore a uno, o addirittura a due o tre, come segno di un sistema di trading profittevole.

La stessa equazione dovrebbe essere applicata a più backtest. Il punto è che qualsiasi backtest in questo caso equivale a un ciclo. Possiamo anche calcolare prima le medie dei cicli e poi calcolare la media delle medie relative ai backtest. Oppure possiamo farlo in modo molto più semplice, massimizzando la durata del segmento di test. Questo approccio vi eviterà almeno di eseguire più test, perché il numero di cicli sarà massimo, il che significa che il fattore di recupero medio sarà calcolato con la massima precisione possibile.

Aumentare l'efficienza dei sistemi con la diversificazione

Limiti utili

Dopo aver preso in considerazione le possibilità di affinare alcune caratteristiche dei backtest, siete indubbiamente meglio equipaggiati, ma non conoscete ancora l'aspetto principale. La base sta nella risposta alla domanda - perché è necessario eseguire tutti questi test multipli o suddividere i cicli? La domanda è davvero complessa se non ci si impegna quanto ho fatto io con il mio tempo. Purtroppo è necessario, ma con il mio aiuto potete ridurre notevolmente il tempo necessario per farlo.

Questa sezione consente di valutare l'oggettività di un particolare parametro. Cercherò di spiegarlo sia teoricamente che utilizzando le equazioni. Cominciamo con l'equazione generale:

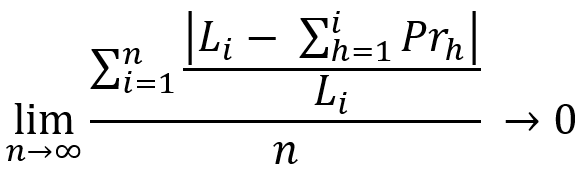
Consideriamo un'equazione simile con alcune leggere modifiche:

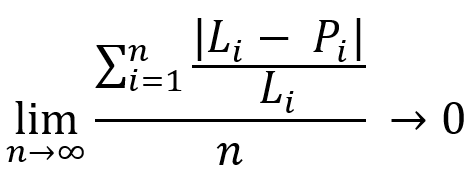
L'essenza di queste equazioni è la stessa. Queste equazioni dimostrano che in qualsiasi sistema di trading redditizio, quando la durata della sezione di test tende all'infinito, otterremo una fusione completa delle linee del saldo e del profitto corrente, con una certa linea che rappresenta il nostro profitto medio. Nella maggior parte dei casi, la natura di questa linea è determinata dalla strategia scelta. Per una comprensione più approfondita, osserviamo l'immagine seguente:

Fig. 4

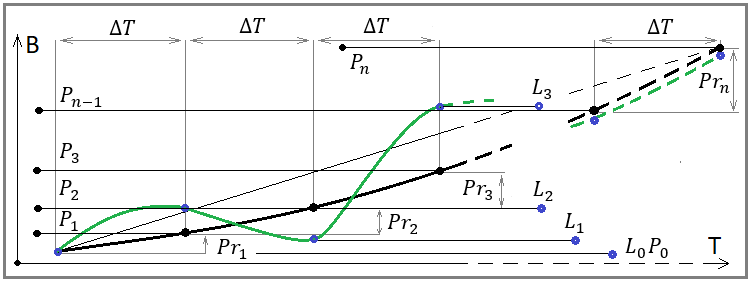
Se osservate attentamente questa immagine, vedrete su di essa tutte le grandezze presenti nelle nostre equazioni. Rivela il significato geometrico dei nostri limiti matematici. L'unica cosa che manca nelle nostre equazioni è l'intervallo di tempo dT. Con questo intervallo, discretizziamo le nostre fasi di saldo e diamo origine a tutti i punti della nostra serie numerica per il saldo e l'utile di questi intervalli, e calcoliamo anche i valori della nostra linea mediana negli stessi punti. Queste equazioni sono l'equivalente matematico della seguente affermazione:

• Più combiniamo insieme test multipli o curve di trading, più assomigliano a una linea ascendente liscia (solo se il sistema è davvero redditizio)

In altre parole, qualsiasi sistema di trading profittevole appare tanto più bello nella parte grafica del tester della strategia o del segnale, quanto più lunga è l'area di test scelta. Qualcuno potrebbe dire che nessun sistema può raggiungere tali indicatori, tuttavia esistono molti esempi sul Mercato, quindi sarebbe sciocco negarlo. Tutto dipende dall'universalità dell'algoritmo e quanto bene si comprende la fisica del mercato. Se si conosce la matematica che è sempre insita nel mercato in cui si opera, si ottiene di fatto una curva di profitto che cresce all'infinito e non è necessario attendere un intero infinito per confermare l'efficacia del sistema. Naturalmente, è chiaro che si tratta di un compito estremamente difficile, ma tuttavia, nell'ambito di molti algoritmi, questo compito è realizzabile.

Concludiamo questa introduzione teorica imparando a utilizzare correttamente le tecniche ricevute. Ci si potrebbe chiedere come utilizzare queste tecniche con somme infinite, quando abbiamo solo campioni limitati e, di conseguenza, anche inevitabili somme incomplete.

1. La risposta sta nella suddivisione dell'intera storia in segmenti
2. Selezionare diversi segmenti con una lunghezza in costante crescita per tutta la durata del test fino a un segmento dell'intera cronologia
3. Scegliere una metodologia di test
4. Test
5. Cercare un miglioramento del fattore di recupero e/o del drawdown relativo.

L'essenza di questo complicato schema di test consiste nel rivelare segni indiretti che i nostri limiti tendono realmente all'infinito e allo zero, rispettivamente. Per aumentare l'efficienza del nostro schema di test, dobbiamo capire che la sezione di test più lunga dovrebbe almeno sembrare più bella di quella più corta, e idealmente ogni sezione successiva dovrebbe essere sia più grande che più bella. Uso il concetto di "più bella" solo per chiarire a tutti che questo equivale in realtà ai nostri limiti.

Tuttavia, i nostri limiti sono validi solo durante le considerazioni teoriche o i preparativi (come preferite). A questo proposito, sorge la domanda: come scoprire questi fatti senza ricorrere "all’analisi oculare"? Dobbiamo in qualche modo adattare i nostri limiti ai parametri che abbiamo nel report del tester della strategia. In altre parole, abbiamo bisogno di limiti alternativi per alcuni parametri del report o del segnale del tester di strategia in modo da poter utilizzare la nostra struttura di test. Permettetemi di mostrarvi l'insieme necessario e sufficiente di limiti alternativi:

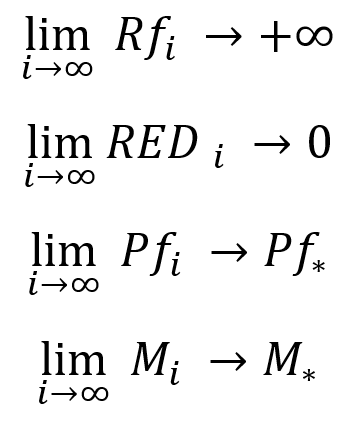
Cosa dobbiamo capire qui:

1. Nel corso di un test infinito, il fattore di recupero di qualsiasi strategia profittevole tende all'infinito.
2. Durante un test infinito, il drawdown relativo per patrimonio netto (di qualsiasi strategia redditizia) tende a zero.
3. Durante un test infinito, il fattore di profitto delle operazioni di qualsiasi strategia profittevole tende al suo valore medio e ha un limite reale finito.
4. Durante un test infinito, l'aspettativa matematica di qualsiasi strategia redditizia senza lotto automatico abilitato (con un lotto fisso) tende al suo valore medio e ha un limite reale finito.

Tutto questo ha a che fare con test infiniti, tuttavia è utile comprendere il significato matematico di questi limiti prima di procedere al loro adattamento a un campione finito. L'adattamento di queste espressioni alla nostra metodologia dovrebbe iniziare con il fatto che dovremmo selezionare diversi segmenti di test, ognuno dei quali dovrebbe essere significativamente più grande del precedente, preferibilmente almeno due volte. Questo è necessario per poter notare la differenza di letture tra test più brevi e più lunghi. Se numeriamo i nostri test in modo tale che, all'aumentare dell'indice, la sua lunghezza cresca nel tempo, otteniamo il seguente adattamento per il caso di campioni finiti:

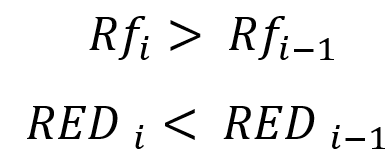
In altre parole, un aumento del fattore di recupero e una diminuzione del drawdown relativo in termini di fondi è una prova indiretta del fatto che, molto probabilmente, l'ulteriore aumento del segmento di test o della durata del segnale rende la nostra curva visivamente più bella. Questo significa che abbiamo confermato la realizzazione dei nostri limiti infiniti. Altrimenti, se la curva dei profitti non diventa più rettilinea, possiamo affermare che il risultato ottenuto è molto vicino alla casualità e la probabilità di perdite in futuro è estremamente elevata.

Naturalmente, molti diranno che basta ottimizzare il sistema più spesso e tutto andrà bene. In alcuni casi estremamente rari è possibile, ma questo approccio richiederà una metodologia di test completamente diversa. Non consiglio a nessuno di ricorrere a questo approccio, perché in questo caso non si ha alcuna matematica, mentre qui si ha tutto in modo chiaro.

Tutte queste sfumature dovrebbero convincervi che il test dell'algoritmo di riacquisto richiede a maggior ragione l'uso di questo approccio. In particolare, possiamo anche semplificare il compito e testare il sistema di riacquisto immediatamente sul segmento di lunghezza massima. Possiamo invertire questa logica. Se non ci piace la performance di trading nel segmento più lungo, anche una performance migliore nei segmenti brevi indicherà che le nostre disuguaglianze non sono più soddisfatte e il sistema non è pronto per il trading in questa fase.

Caratteristiche utili in termini di utilizzo parallelo di più strumenti

Quando si esegue un test su uno storico limitato, sorge certamente la domanda: esiste uno storico sufficiente per utilizzare correttamente la nostra metodologia di test? Il fatto è che in molti casi la strategia ha un peso, ma la sua qualità non è sufficientemente elevata per un uso confortevole. Per cominciare, dovremmo almeno capire se ha davvero un inizio predittivo e se possiamo iniziare a impegnarci nella sua modernizzazione. In alcuni casi, non abbiamo letteralmente abbastanza storico di trading disponibile. Che cosa dobbiamo fare? Come molti hanno già intuito, a giudicare dal titolo della sottosezione, dovremmo utilizzare più strumenti per questo scopo. 

Sembrerebbe un'ovvietà, ma purtroppo, come sempre, non c'è matematica da nessuna parte. L'essenza del test su più strumenti è equivalente alla stessa essenza per aumentare la durata del test. L'unica modifica è che il sistema deve essere multivaluta. Il sistema può avere differenti impostazioni per i vari strumenti di trading, ma è auspicabile che tutte le impostazioni siano simili. La somiglianza delle impostazioni rappresenta il fatto che il sistema utilizza principi fisici che funzionano sul massimo numero possibile di strumenti di trading.

Con questo approccio e la corretta implementazione di tali prove, l'indice "i" dovrebbe già essere inteso come il numero di strumenti testati simultaneamente su un segmento di prova fisso. Le espressioni avranno il seguente significato:

1. Quando si aumenta il numero di strumenti negoziati, maggiore è il numero di strumenti, maggiore è il fattore di recupero.
2. Aumentando il numero di strumenti negoziati, maggiore è il numero di strumenti, minore è il drawdown relativo per il patrimonio netto.

In effetti, un aumento del numero di test può essere interpretato, per semplicità, come un aumento della durata totale dei test, come se considerassimo ogni test per ogni strumento come parte di un enorme test complessivo. Questa astrazione vi aiuterà a capire perché anche questo approccio ha la stesso valore. Ma se consideriamo questo problema in modo più accurato e comprendiamo più a fondo perché una linea composta da più uno sarà molto più bella, allora dovremmo utilizzare i seguenti concetti della teoria della probabilità:

• Valore casuale
• Varianza di una variabile casuale
• Aspettativa matematica di una variabile casuale
• La legge di distribuzione normale di una variabile casuale

Per spiegare appieno perché abbiamo bisogno di tutto questo, abbiamo bisogno di un'immagine che ci aiuti a guardare un backtest o un segnale di trading in modo un po' diverso:

Fig. 5

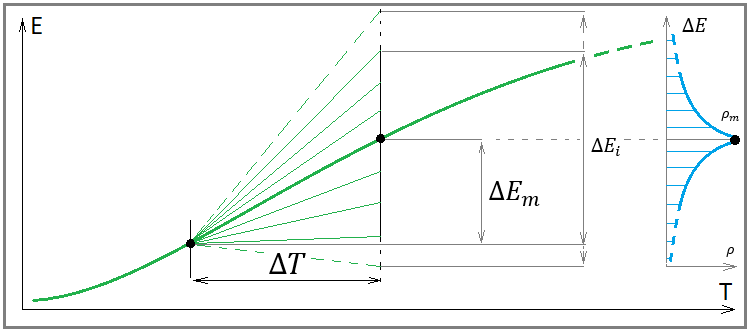
Non traccerò una linea del saldo qui, perché in questo caso non è determinante e ci serve solo una linea di profitto. Il significato di questa immagine è che per ogni linea di profitto è possibile selezionare un numero infinito di segmenti indipendenti di lunghezza fissa, in cui è possibile costruire la legge di distribuzione di una variabile casuale dell'incremento della linea di profitto. La presenza di una variabile casuale significa che in futuro l'incremento di profitto nell'area selezionata può avere valori completamente diversi nell'intervallo più ampio.

Suona complicato, ma in realtà è tutto semplice. Credo che molti abbiano sentito parlare della legge di distribuzione normale. Si suppone che descriva quasi tutti i processi casuali in natura. Credo che questa non sia altro che un'illusione inventata per impedirvi di "pensare". A parte gli scherzi, le ragioni della popolarità della legge di distribuzione sono che si tratta di un'equazione compilata artificialmente e molto comoda per descrivere distribuzioni simmetriche rispetto all'aspettativa matematica di una variabile casuale. Ci sarà utile per ulteriori trasformazioni matematiche ed esperimenti.

Tuttavia, prima di iniziare a lavorare con questa legge, dobbiamo definire la proprietà principale di qualsiasi legge di distribuzione di una variabile casuale:

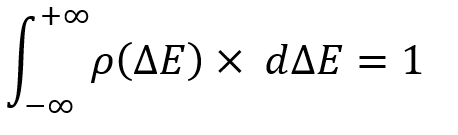
Qualsiasi legge di distribuzione di una variabile casuale è essenzialmente l'analogo dell'intero gruppo di eventi non congiunti. L'unica differenza è che non abbiamo un numero fisso di questi eventi e in qualsiasi momento possiamo selezionare qualsiasi evento di interesse come questo:

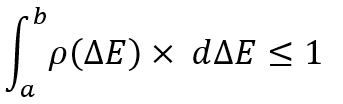
Tecnicamente, questo integrale considera la probabilità di trovare una variabile casuale nell'intervallo indicato di una variabile casuale e naturalmente non può essere maggiore di uno. Nessun evento totale di un dato spazio degli eventi può avere una probabilità maggiore di uno. Tuttavia, questo non è l'aspetto più importante. L'unica cosa importante è capire che in questo caso l'evento è determinato solo da un insieme di due numeri. Questi sono esempi di variabili casuali di dimensione minima.

Esistono analoghi di queste equazioni per la dimensione "N", quando un evento può essere determinato da "N*2" numeri e costruzioni ancora più complesse (nel quadro degli integrali di regioni multidimensionali). Si tratta di sezioni di matematica piuttosto complesse, ma in questo caso sono ridondanti. Tutte le leggi ottenute sono autosufficienti per la variante monodimensionale.

Prima di passare a costruzioni più complesse, ricordiamo alcune caratteristiche dei parametri delle leggi di distribuzione dei valori casuali:

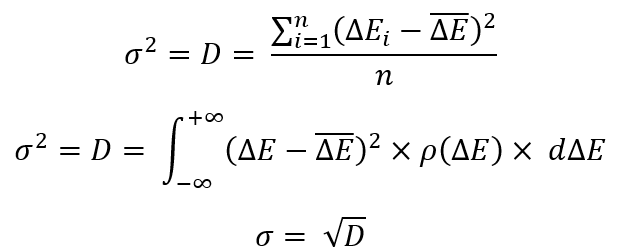
Per definire una qualsiasi di queste equazioni, dobbiamo determinare la cosa più importante: l'aspettativa matematica di una variabile casuale. Nel nostro caso, si presenta come segue:

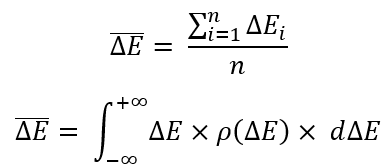
L'aspettativa matematica è semplicemente la media aritmetica. Ai matematici piace dare nomi molto intelligenti a cose semplici, in modo che nessuno capisca nulla. Ho fornito due equazioni. L'unica differenza è che il primo lavora su un numero finito di variabili casuali (quantità limitata di dati), mentre nel secondo caso si utilizza l'integrale sulla "densità di probabilità".

Un integrale è l'equivalente di una somma, con l'unica differenza che somma un numero infinito di variabili casuali. La legge di distribuzione di una variabile casuale, che si trova sotto l'integrale e contiene l'intera infinità di variabili casuali. Ci sono alcune differenze, ma in generale l'essenza è la stessa.

Torniamo ora alle equazioni precedenti. Queste sono solo alcune manipolazioni con le leggi di distribuzione delle variabili casuali che sono convenienti per la maggior parte dei matematici. Come nell'ultimo esempio, esistono due implementazioni - una per un insieme finito di variabili casuali, l'altra per un insieme infinito (la legge di distribuzione di una variabile casuale). Si afferma che "D" è il quadrato medio della differenza tra tutte le variabili casuali e la variabile casuale media (l'aspettativa matematica della variabile casuale). Questo valore è chiamato "dispersione". La radice di questo valore è chiamata "deviazione standard".

Distribuzione normale di una variabile casuale

Sono questi i valori generalmente accettati nella matematica delle variabili casuali. Sono considerati i più convenienti per descrivere le caratteristiche più importanti delle leggi di distribuzione casuale. Non sono d'accordo con questo concetto, ma sono comunque obbligato a mostrarvi come vengono calcolati. Alla fine, queste grandezze saranno necessarie per comprendere la legge di distribuzione normale. È improbabile che possiate trovare facilmente queste informazioni, ma vi dirò che la legge di distribuzione normale è stata inventata artificialmente con pochi obiettivi:

• Un modo semplice per determinare la legge di distribuzione simmetrica all'aspettativa matematica
• Possibilità di impostare la dispersione e la deviazione standard
• Possibilità di definire le aspettative matematiche

Tutte queste opzioni ci permettono di ottenere un'equazione già pronta per la legge di distribuzione di una variabile casuale, chiamata legge di distribuzione normale:

Esistono altre varianti delle leggi di distribuzione delle variabili casuali. Ogni implementazione è inventata per una certa gamma di problemi, ma poiché la legge normale è la più popolare e conosciuta, la useremo come esempio per dimostrare e compilare l'equivalente matematico delle seguenti affermazioni:

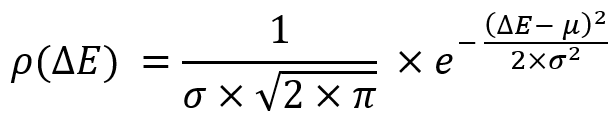
• Più strumenti vengono negoziati in parallelo per un sistema profittevole, più bello e lineare sarà il nostro grafico dei profitti (un caso speciale di diversificazione).
• Più lunga è l'area selezionata per il test o il trading, più bello e lineare è il nostro grafico dei profitti.
• Maggiore è il numero di sistemi paralleli tradati con redditività comprovata, più dritto e bello è il nostro grafico di profittabilità complessiva.
• La combinazione di tutti questi elementi dà luogo a una diversificazione ideale e ad un bel grafico

Tutto ciò che è stato detto si applica solo ai sistemi di trading la cui redditività è stata dimostrata matematicamente e praticamente. Iniziamo definendo cosa significa "il grafico più bello" in termini matematici. La "deviazione standard", la cui equazione ho già mostrato sopra, può aiutarci in questo senso.

Se abbiamo una famiglia di curve di densità di distribuzione per una variabile casuale di incremento del profitto con la stessa aspettativa matematica, che simboleggiano due segmenti della stessa durata nel tempo, per due grafici praticamente identici, allora preferiremmo quella con la deviazione standard più piccola. La curva perfetta in questa famiglia potrebbe essere quella con deviazione standard pari a zero. Questa curva è realizzabile solo se conosciamo il futuro, il che è impossibile, tuttavia dobbiamo capirlo per poter confrontare le curve di questa famiglia.

Bellezza della curva di profitto nel quadro della legge di distribuzione dei valori casuali

Questo fatto è comprensibile quando abbiamo a che fare con una famiglia di curve, dove le aspettative matematiche dell'incremento del profitto nel periodo di tempo selezionato sono le stesse, ma cosa fare quando abbiamo a che fare con curve di distribuzione completamente arbitrarie? Non è chiaro come confrontarle. A questo proposito, la deviazione standard non è più perfetta e abbiamo bisogno di un altro valore di confronto più universale che tenga conto della scalabilità, oppure dobbiamo trovare un algoritmo per ridurre queste leggi di distribuzione a un certo valore relativo, in cui tutte le distribuzioni avranno la stessa aspettativa matematica e, quindi, i criteri classici si applicheranno a tutte le curve. Ho sviluppato un algoritmo di questo tipo. Uno dei trucchi è la seguente trasformazione:

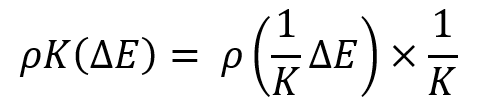
La famiglia di queste curve sembrerà qualcosa del genere:

Fig. 6

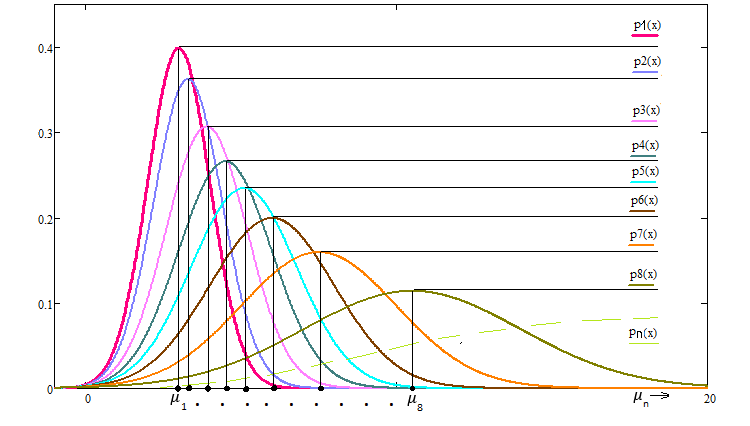
Un fatto molto interessante è che se sottoponiamo la legge della distribuzione normale a questa trasformazione, allora essa è invariante rispetto a questa trasformazione e avrà il seguente aspetto:

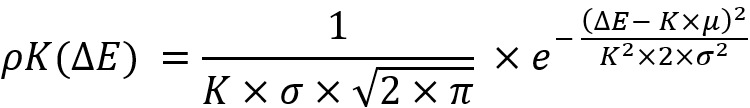
L'invarianza consiste nelle seguenti sostituzioni:

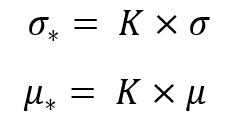
Se sostituiamo queste sostituzioni nell'equazione precedente, otteniamo la stessa legge di distribuzione che opera con i valori corrispondenti contrassegnati dagli asterischi:

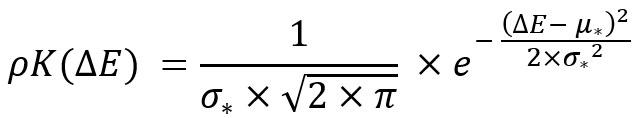
Questa trasformazione è necessaria per garantire non solo l'invarianza della legge di trasformazione, ma anche l'invarianza del parametro successivo:

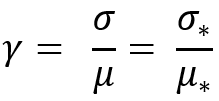
Ho dovuto inventare questo parametro. È impossibile scalare correttamente la legge di distribuzione normale, come qualsiasi altra legge, senza di essa. Questo parametro sarà invariante anche per qualsiasi altra legge di distribuzione. In effetti, la legge normale è più facile da percepire e comprendere. La sua idea è che può essere utilizzata per qualsiasi distribuzione con aspettative matematiche differenti e la sua essenza sarà simile alla deviazione standard, solo senza il requisito che tutte le distribuzioni confrontate devono avere la stessa aspettativa matematica. Si scopre che la nostra trasformazione è progettata per ottenere una famiglia di distribuzioni in cui un dato parametro ha lo stesso valore. Sembra piuttosto conveniente, non è vero?

Questo è un modo per definire la cosiddetta bellezza del grafico. Il sistema con il parametro più piccolo è "il più bello". Tutto ciò va bene, ma questo parametro ci serve per un altro scopo. Il compito era quello di confrontare la bellezza dei due sistemi. Immaginiamo di avere due sistemi che tradano in modo indipendente. Quindi, il nostro obiettivo è quello di unire questi sistemi e capire se ci sarà un effetto da questa fusione, o meglio, sperare che sia il seguente:

 

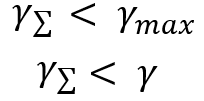
Questi rapporti si osservano quando si utilizza una qualsiasi legge di distribuzione. Ciò significa automaticamente che ha senso diversificare se i nostri strumenti o sistemi negoziati in parallelo hanno una redditività simile. Dimostreremo questo fatto in modo un po' diverso. Come ho detto, ho elaborato un algoritmo per ridurre tutte le distribuzioni a un valore casuale relativo. Lo utilizzeremo, ma prima analizzeremo il processo generale di fusione di diverse linee, nell'ambito della legge di distribuzione di una variabile casuale che rappresenta la somma di due delta. Si tratta di una logica ricorrente per la fusione a coppie. A tal fine, assumiamo di avere "n+1" curve, ognuna delle quali ha un'aspettativa matematica definita. Ma per arrivare alla variabile casuale che simboleggia la fusione, dobbiamo capire questo:

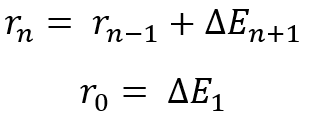
In realtà, si tratta di un'espressione ricorrente priva di senso matematico, ma che mostra la logica dell'unione di tutte le variabili casuali presenti nell'elenco. In parole povere, abbiamo "n+1" curve, che dobbiamo combinare utilizzando "n" trasformazioni successive. In effetti, ciò significa che dobbiamo ottenere la legge di distribuzione della variabile casuale totale in ciascuna fase utilizzando qualche tipo di operatore di trasformazione.

Non mi dilungherò in lunghe spiegazioni. Mi limiterò invece a mostrare questi operatori di conversione in modo che possiate trarre le vostre conclusioni. Queste equazioni implementano la fusione di due curve di profitto nel periodo di tempo selezionato e calcolano la probabilità che il profitto totale dei due segmenti delle curve "dE1 + dE2" sia rispettivamente inferiore (Pl) e superiore (Pm) al valore "r" selezionato:

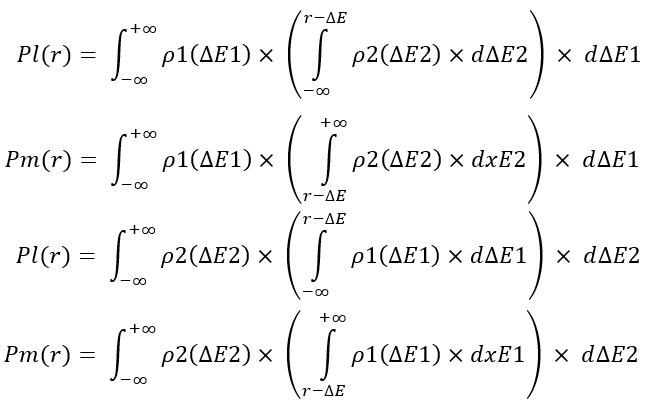
Per l'implementazione di queste grandezze ci sono due opzioni. Entrambe sono completamente simili. Una volta calcolate, questi valori possono essere utilizzati per ottenere la legge di distribuzione della variabile casuale "r", che è ciò che ci viene richiesto per elaborare l'intera catena di fusione ricorrente. Per definizione di variabile casuale, da queste equazioni possiamo ottenere le corrispondenti leggi di distribuzione come segue:

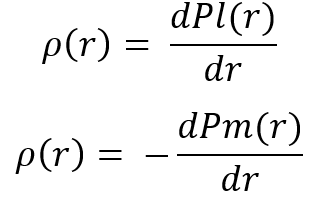
Come avrete intuito, dopo aver ottenuto la legge di distribuzione, possiamo procedere al passo successivo della catena di trasformazioni ricorrenti. Dopo aver lavorato attraverso l'intera catena, otteniamo la distribuzione finale, che possiamo già confrontare con una delle distribuzioni utilizzate per la catena di fusione ricorrente. Creiamo un paio di distribuzioni basate sulle leggi che abbiamo ottenuto ed eseguiamo una fase di fusione come esempio per dimostrare che ogni fusione è "più bella della precedente":

Fig. 7

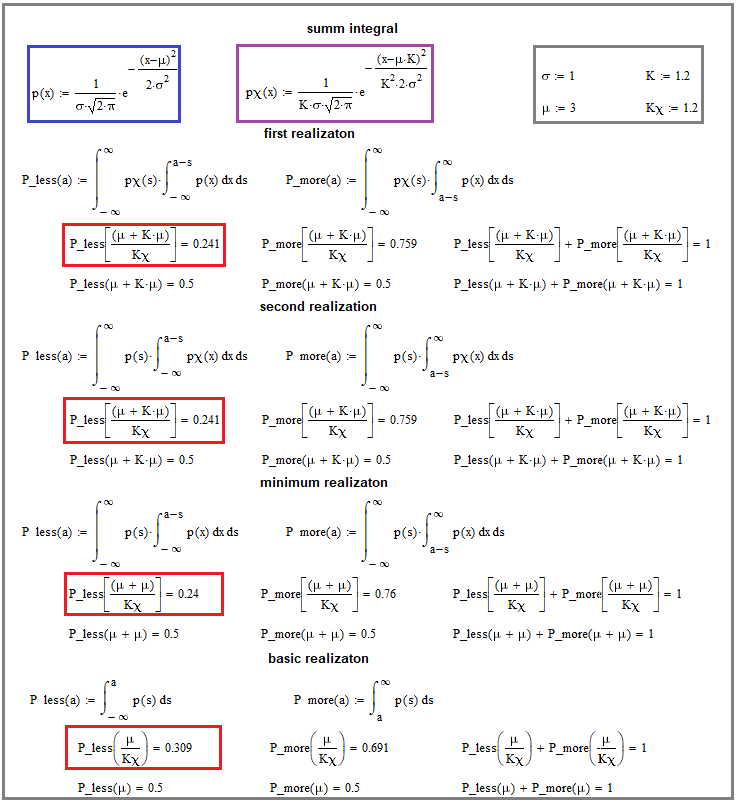
L'immagine mostra la fusione matematica che applica le nostre equazioni di fusione. L'unica cosa che non viene mostrata è la differenziazione per trasformare gli integrali in leggi di una distribuzione casuale dei valori di fusione. Vedremo il risultato della differenziazione più avanti, nell'ambito di un'idea più generale, ma per ora occupiamoci di ciò che è presente nell'immagine.

Prestate attenzione ai rettangoli rossi. Sono la base di partenza qui. L'integrale inferiore dice che prendiamo l'integrale secondo la legge di distribuzione originale in modo da calcolare la probabilità che la variabile casuale assuma un valore minore dell'aspettativa matematica divisa per "Kx". Qui sopra sono riportati integrali simili per le fusioni di due distribuzioni leggermente diverse. In tutti i casi, è importante mantenere questo rapporto (Kx) tra l'aspettativa matematica e il valore limite scelto dell'integrale, che è espresso nel corrispondente "Kx". 

Notare che sono presenti entrambe le opzioni di fusione, secondo le equazioni date sopra. Inoltre, vi è una fusione della distribuzione di base con se stessa, come se stessimo unendo due curve di profitto simili. Simile non significa identico nell'immagine, ma piuttosto avere leggi di distribuzione identiche per la variabile casuale dell'incremento della curva dei profitti nel periodo di tempo selezionato. La prova è che abbiamo trovato una probabilità minore di deviazione relativa della variabile casuale di fusione rispetto all'originale. Questo significa che abbiamo una legge più "bella" per l'incremento di un valore di profitto casuale in qualsiasi fusione. Naturalmente ci sono eccezioni che richiedono un approfondimento dell'argomento, ma penso che questo approccio sia sufficiente per l'articolo. Molto probabilmente non troverete niente di meglio da nessuna parte, perché si tratta di un materiale molto specifico.

Il modo alternativo per confrontare la bellezza è quello di trasformarle tutte, sia le leggi di distribuzione originali che il risultato della catena ricorrente considerata in precedenza. Per ottenere questo risultato, basta utilizzare la nostra trasformazione, che ci ha permesso di ottenere una famiglia di curve di distribuzione scalabili, e procedere come segue:

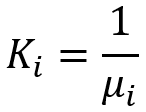
Il trucco di questa trasformazione è che con questo approccio, tutte le leggi di distribuzione sottoposte alla trasformazione corrispondente, avranno la stessa aspettativa matematica e, di conseguenza, potremo usare solo la deviazione standard per valutare la loro "bellezza" senza dover inventare alcun criterio esotico. Vi ho mostrato due metodi. Sta a voi scegliere quello che meglio si adatta a voi. Come avrete intuito, le leggi di distribuzione di tutte queste curve relative avranno l'aspetto seguente:

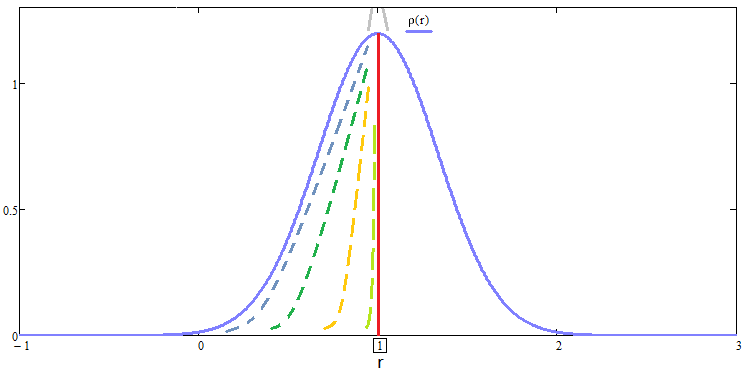
Questo approccio è anche applicabile ai test estesi. Per test estesi si intende il test su un segmento più lungo. Questa applicazione è adatta solo per confermare il fatto che piùlungo è il test, più bello è il grafico. L'unico trucco per questa prova che dovete applicare è accettare che se aumentiamo la durata del test, allora lo facciamo in multipli di un numero intero, mentre in multipli di questo numero consideriamo già non 1 passo ma "n" e applichiamo le equazioni di fusione. Questa fusione sarà ancora più semplice, poiché la catena di fusione ricorrente conterrà un solo elemento duplicato e sarà possibile confrontare il risultato solo con questo elemento.

Conclusioni

Nell'articolo non abbiamo preso in considerazione l'algoritmo di riacquisto in sé, ma piuttosto un argomento molto più importante che fornisce le equazioni matematiche e i metodi necessari per una valutazione più accurata ed efficiente dei sistemi di trading. Ma soprattutto, si ottiene la prova matematica di quanto vale la diversificazione, di cosa la rende efficace e di come aumentarla in modo naturale e sano, sapendo che si sta facendo tutto giusto.

Abbiamo anche dimostrato che il grafico di qualsiasi sistema profittevole è tanto più bello quanto più lunga è l'area di trading che utilizziamo, e anche che più sistemi profittevoli operano simultaneamente su un conto. Finora tutto è stato inquadrato in forma teorica, ma nel prossimo articolo considereremo gli aspetti applicativi. In parole povere, costruiremo un modello matematico funzionante per la simulazione dei prezzi e la simulazione del trading multivalutario e confermeremo tutte le nostre conclusioni teoriche. Molto probabilmente non troverete questa teoria da nessuna parte, quindi cercate di approfondire questa matematica, o almeno di capirne l'essenza.