cool
merci pour l'article !
Un script bien pratique, merci.
J'en ai fait quelques uns aussi :
ReLu + Sigmoïde + Décalage pour capturer la sortie de 0.0 à 1.0 (entrée -12 à 12)
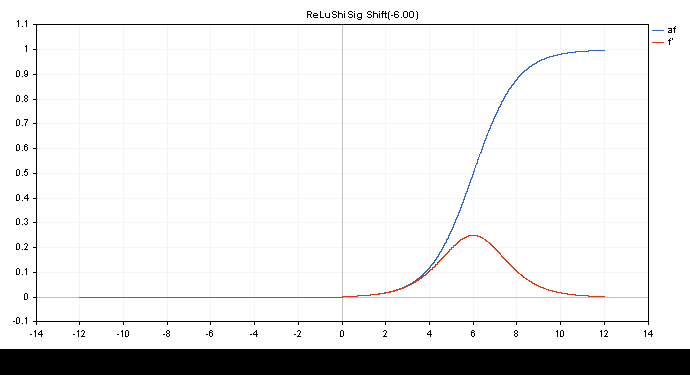
double activationSigmoid(double x){ return(1/(1+MathExp(-1.0*x))); } double derivativeSigmoid(double activation_value){ return(activation_value*(1-activation_value)); } double activationReLuShiSig(double x,double shift=-6.0){ if(x>0.0){ return(activationSigmoid(x+shift)); } return(0.0); } double derivativeReLuShiSig(double output){ if(output>0.0){ return(derivativeSigmoid(output)); } return(0.0); }
Exponentielle limitée .af=f' (entrée -5.0 à 5.0)
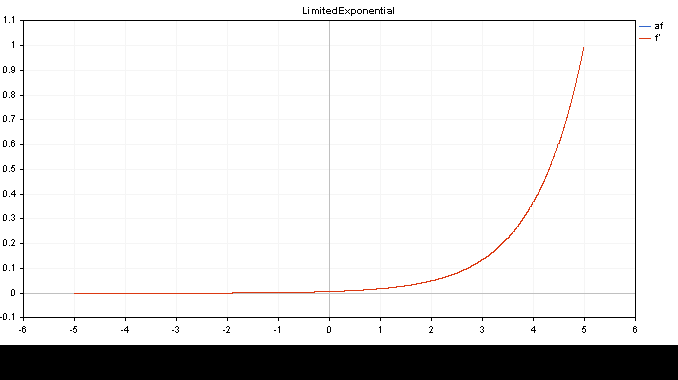
double activationLimitedExponential(double x){ return(MathExp(x)/149.00); } //et la dérivée est elle-même double derivativeLimitedExponential(double x){ return(x); }
👨🔧
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Un nouvel article Matrices et vecteurs en MQL5 : Fonctions d'activation a été publié :
Nous ne décrirons ici qu'un seul des aspects de l'apprentissage automatique, à savoir les fonctions d'activation. Dans les réseaux neuronaux artificiels, la fonction d'activation d'un neurone calcule la valeur d'un signal de sortie en fonction des valeurs d'un signal d'entrée ou d'un ensemble de signaux d'entrée. Nous nous pencherons sur les rouages du processus.
Les graphiques de la fonction d'activation et leurs dérivés ont été préparés dans une séquence monotone croissante de -5 à 5 à titre d'illustration. Le script affichant le graphique des fonctions sur le graphique des prix a également été développé. La boîte de dialogue d'ouverture de fichier s'affiche pour spécifier le nom de l'image enregistrée en appuyant sur la touche Page suivante.
La touche ESC met fin au script. Le script lui-même est attaché ci-dessous.
Auteur : MetaQuotes