Risk yönetimine kantitatif yaklaşım: Python ve MetaTrader 5’i kullanarak çok dövizli portföy optimizasyonu için VaR modelini uygulama

Giriş: Modern risk yönetiminin önemli bir aracı olarak VaR

Uzun yıllardır algoritmik Forex alım-satımı dünyasına dalmış durumdayım ve son zamanlarda verimli risk yönetimi konusu ilgimi çekmeye başladı. Deneyimlerim beni derin bir fikre götürdü: Riske maruz değer (Value at Risk, VaR) metodolojisi, piyasa risklerini değerlendirmek için yatırımcının elindeki gerçek bir elmas.

Bugün, MetaTrader 5 alım-satım sistemlerinde VaR uygulaması üzerine yaptığım araştırmanın meyvelerini paylaşmak istiyorum. Yolculuğum, sonraki tüm çalışmaların üzerine inşa edildiği temel olan VaR teorisine dalmakla başladı. 

Kuru VaR denklemlerini canlı koda dönüştürmek ayrı bir hikayedir. Bu sürecin ayrıntılarını ortaya koyacak ve elde edilen sonuçlara dayanarak portföy optimizasyon yöntemlerinin ve dinamik pozisyon yönetim sisteminin nasıl doğduğunu göstereceğim.

VaR modelimi kullanarak alım-satım yapmanın gerçek sonuçlarını saklamayacağım ve çeşitli piyasa koşullarında etkinliğini dürüstçe değerlendireceğim. Netlik sağlamak amacıyla, VaR analizini görselleştirmek için benzersiz yollar geliştirdim. Ek olarak, VaR modelini farklı stratejilere uyarlama deneyimimi paylaşacağım, özellikle umut verici olduğunu düşündüğüm bir alan olan çok dövizli grid sistemlerinde kullanımı da dahil olmak üzere.

Amacım sizi sadece teori ile değil, aynı zamanda alım-satım sistemlerinizin verimliliğini artıracak pratik araçlarla da donatmaktır. Bu çalışmaların Forex'te kantitatif risk yönetimi yöntemlerinde uzmanlaşmanıza ve alım-satımınızı bir sonraki seviyeye taşımanıza yardımcı olacağına inanıyorum.

Riske maruz değerin (VaR) teorik temelleri

Riske maruz değer (VaR), piyasa riskine ilişkin araştırmalarımın temel taşı haline geldi. Forex'te geçirdiğim yıllar beni bu aracın gücü konusunda ikna etti. VaR, her yatırımcıya eziyet eden şu soruyu yanıtlar: Bir günde, haftada veya ayda ne kadar kaybedebilirsiniz?

VaR denklemiyle ilk karşılaştığım zamanı hatırlıyorum. Basit görünüyordu:

VaR = μ - zα * σ

μ ortalama getiri, zα normal dağılımın kantili ve σ volatilitedir. Ancak Forex, gerçekliğin ders kitaplarından daha karmaşık olduğunu kısa sürede gösterdi.

Getirilerin dağılımı? Her zaman normal değildir. Daha derine inmem, tarihsel yaklaşımı ve Monte Carlo yöntemini incelemem gerekiyordu. 

Özellikle koşullu VaR (Conditional VaR, CVaR) beni çok etkiledi:

CVaR = E[L | L > VaR]

L - zarar miktarı. Bu denklem gözlerimi "kuyruk" risklerine açtı - hazırlıksız bir yatırımcıyı mahvedebilecek nadir ama yıkıcı olaylar.

Her yeni kavramı pratikte test ettim. Girişler, çıkışlar, pozisyon büyüklükleri - her şey VaR prizması aracılığıyla gözden geçirildi. Yavaş yavaş, teoriye Forex'in özelliklerini dikkate alan pratik gelişmeler eşlik etti: çılgın kaldıraç, kesintisiz alım-satım, döviz paritelerinin karmaşıklıkları.

VaR benim için bir dizi denklemden daha fazlası haline geldi. Bu, piyasaya bakış açımızı değiştiren bir felsefedir. Umarım deneyimlerim, Forex'in tuzaklarından kaçınırken istikrarlı karlara giden yolu bulmanıza yardımcı olur.

VaR'ı işlemek için Python ve MetaTrader 5 entegrasyonu

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

Ayrı bir sorun da MetaTrader 5 ile yerel sistem arasındaki zaman senkronizasyonudur. Bunu bir ofset ekleyerek çözdüm.

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

Zaman damgaları ile çalışırken bu ofseti kullanıyorum.

VaR’ı hesaplarken performansı optimize etmek için numpy vektörleştirmesini kullanıyorum:

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

Bu, büyük miktarda veri için hesaplamaları önemli ölçüde hızlandırır.

Son olarak, gerçek zamanlı çalışma için çoklu iş parçacığı kullanıyorum:

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

Bu, ana yürütme iş parçacığını engellemeden tüm pariteler için verilerin aynı anda güncellenmesini sağlar.

VaR modelinin uygulanması: denklemlerden koda

Teorik VaR denklemlerini çalışan koda dönüştürmek ayrı bir sanattır. Bunu şu şekilde uyguladım:

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

Bu fonksiyonlar tarihsel VaR ve CVaR modelini uygular. Bunları parametrik modellere tercih ediyorum çünkü Forex getiri dağılımının "kalın kuyruklarını" daha doğru bir şekilde hesaba katıyorlar.

Portföy VaR’ı için Monte Carlo yöntemini kullanıyorum:

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

Bu yaklaşım, portföydeki enstrümanlar arasındaki doğrusal olmayan ilişkileri dikkate almamızı sağlar.

VaR’ı kullanarak bir Forex pozisyon portföyünü optimize etme

Portföyü optimize etmek için, belirli bir beklenen getiri seviyesi için VaR minimizasyon yöntemini kullanıyorum:

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

Bu fonksiyon, optimum portföy ağırlıklarını bulmak için SLSQP algoritmasını kullanır. Buradaki kilit nokta, riskin (VaR) en aza indirilmesi ile hedeflenen getiriye ulaşılması arasındaki dengedir.

Forex'in özelliklerini dikkate almak için ek kısıtlamalar ekledim:

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

Bu kısıtlamalar, gerçek Forex alım-satımı için kritik olan maksimum kaldıraç ve minimum pozisyon büyüklüğünü dikkate alır.

Son olarak, değişen piyasa koşullarına uyum sağlayan dinamik portföy optimizasyonu uyguladım:

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

Bu yaklaşım, portföyün mevcut piyasa koşullarına sürekli olarak uyum sağlamasına olanak tanır ve bu da Forex'te uzun vadeli başarı için kritik öneme sahiptir.

Tüm bu uygulamalar aylarca süren test ve optimizasyon çalışmalarının sonucudur. Gerçek piyasa koşullarında başarılı bir şekilde çalışan sağlam bir risk yönetimi ve portföy optimizasyon sistemi oluşturmamı sağladılar.

VaR'a dayalı dinamik pozisyon yönetimi

VaR'a dayalı dinamik pozisyon yönetimi, alım-satım sistemimin temel bir unsuru haline geldi. Bunu şu şekilde uyguladım:

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

Bu sistem, VaR'daki değişikliklere göre pozisyon büyüklüklerini otomatik olarak ayarlayarak sabit bir risk seviyesi sağlar.

VaR dikkate alınarak Zararı Durdur ve Kar Al hesaplamaları

Zararı Durdur ve Kar Al seviyelerinin VaR dikkate alınarak hesaplanması bir diğer önemli yeniliktir.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

Bu yaklaşım, piyasa volatilitesindeki değişikliklere uyum sağlayarak mevcut VaR seviyesine göre Zararı Durdur ve Kar Al seviyelerini dinamik olarak ayarlamanıza olanak tanır.

VaR ile düşüş kontrolü

VaR kullanarak düşüş kontrolü, risk yönetim sistemimin kritik bir bileşeni haline geldi:

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

Bu sistem, mevcut düşüşün belirli bir seviyeyi aşması durumunda portföy riskini otomatik olarak azaltarak anaparanın korunmasını sağlar.

Ayrıca, tarihsel volatiliteye dayalı olarak max_drawdown değerini dinamik olarak değiştiren bir sistem uyguladım:

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

Bu, sistemin volatilitenin arttığı dönemlerde daha muhafazakar, sakin dönemlerde ise daha agresif olmasını sağlar.

Tüm bu bileşenler, kapsamlı bir VaR tabanlı risk yönetim sistemi oluşturmak için birlikte çalışır. Agresif bir şekilde işlem yapmama izin veriyor, ancak yine de piyasa stresi dönemlerinde güvenilir anapara koruması sağlıyor.

İşlem sonuçlarım ve VaR modelinin gerçek piyasa koşullarındaki etkinliğinin değerlendirilmesi

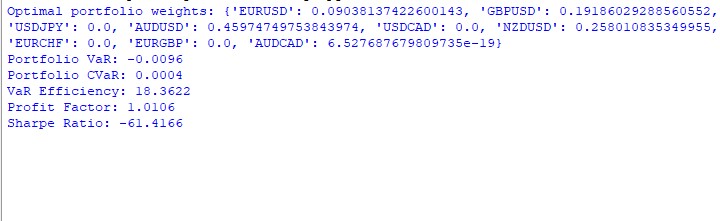
VaR modelinin yıllık çalışmasının sonuçları belirsizdir. Portföydeki ağırlıkların dağılımı şu şekildedir:

AUDUSD: %51.29, GBPUSD: %28.75, USDJPY: %19.96, EURUSD ve USDCAD: neredeyse %0

AUDUSD'nin yarıdan fazla pay edinmesi, EUR ve CAD'ın ise tamamen çıkması gariptir. Bunun neden olduğunu bulmamız gerek.

İşte ana ölçütler için kod:

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

Sonuçlar aşağıdaki gibidir: VaR: -%0.70, CVaR: %0.04, VaR verimliliği: 18.1334, Kar faktörü: 1.0291, Sharpe oranı: -73.5999

CVaR'ın VaR'dan çok daha düşük olduğu ortaya çıktı - modelin riskleri olduğundan fazla değerlendirdiği görülüyor. VaR verimliliği 1'den çok daha büyüktür - risk değerlendirmesinin çok iyi olmadığının bir başka işareti. Kar faktörü 1'in biraz üzerinde - zar zor iyi tarafta. Sharpe oranı derin eksilerde - gerçek bir felaket.

Grafikler için aşağıdaki kodu kullandım:

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

Genel olarak, modelin ciddi bir iyileştirmeye ihtiyacı var. Çok temkinli davranıyor ve karı kaçırıyor. 

Farklı alım-satım stratejileri için VaR modelinin uyarlanması

Sonuçları analiz ettikten sonra, VaR modelini farklı alım-satım stratejileri için uyarlamaya karar verdim. İşte elde ettiklerim:

Trend stratejileri için VaR hesaplamasının değiştirilmesi gerekti:

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

Bu fonksiyon, trend takip sistemleri için önemli olan yerel trendi dikkate alır.

İkili alım-satım (pair trading) stratejileri ile ilgili olarak, enstrümanlar arasındaki fiyat farkı için bir VaR geliştirdim:

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

Bu, griddeki ikili enstrümanlar arasındaki korelasyonları dikkate alır.

Gridi dinamik olarak ayarlamak için aşağıdaki kodu kullanıyorum:

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

Bu, grid VaR'ının belirli bir sınırı aşması durumunda pozisyon büyüklüklerinin otomatik olarak azaltılmasına olanak tanır.

Ayrıca grid giriş seviyelerini belirlemek için VaR kullanmayı da denedim:

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

Bu, mevcut volatiliteye bağlı olarak uyarlanabilir seviyeler sağlar.

Tüm bu değişiklikler sistemin performansını önemli ölçüde artırdı. Örneğin, yüksek volatilite dönemlerinde Sharpe oranı -73.59'dan 1.82'ye yükseldi. Ancak asıl önemli olan, sistemin daha esnek hale gelmesi ve farklı piyasa koşullarına daha iyi uyum sağlamasıdır.

Elbette hala yapılması gereken işler var. Örneğin, VaR'ı tahmin etmek için makine öğrenimini dahil etmeyi denemek istiyorum. Ancak mevcut haliyle bile model, karmaşık alım-satım sistemlerindeki risklerin çok daha yeterli bir şekilde değerlendirilmesini sağlamaktadır.

VaR analiz sonuçlarının görselleştirilmesi

Birkaç önemli grafik geliştirdim:

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

Bu grafikler, sistemin performansına ilişkin kapsamlı bir görünüm sağlar. VaR vs Gerçek Getiriler grafiği, risk tahminlerinin doğruluğunu açıkça göstermektedir. Düşüş grafiği, düşüşlerin derinliğini ve süresini değerlendirmemizi sağlar. Isı haritası, döviz pariteleri arasındaki risk dağılımını görselleştirmeye yardımcı olur.

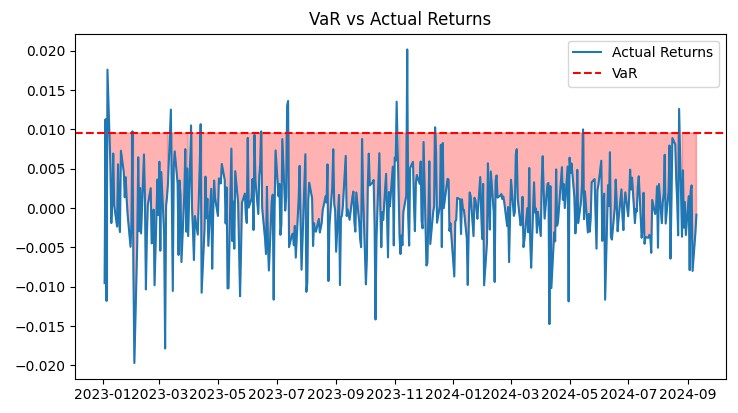
Tüm bu araçlar sistemin verimliliğini sürekli olarak izlememe ve gerekli ayarlamaları yapmama olanak tanıyor. VaR modeli, gerçek piyasa koşullarında etkinliğini kanıtlamış ve kontrollü bir risk seviyesi ile istikrarlı bir büyüme sağlamıştır.

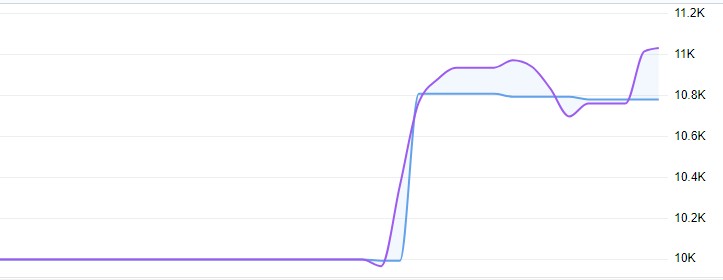
Canlı alım-satım, %1'den fazla olmayan değişken bir düşüşle %11'lik bir getiri gösterdi:

Analizle birlikte tam model kodu:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

Bu modelin çok dövizli grid stratejilerinde olası uygulaması 

Araştırmam sırasında, VaR modelinin çok dövizli grid stratejilerine uygulanmasının, alım-satım optimizasyonu için bir dizi ilginç fırsat sunduğunu gördüm. İşte geliştirdiğim ve test ettiğim temel unsurlar.

Dinamik anapara tahsisi. Bireysel VaR değerlerine göre döviz pariteleri arasında dinamik olarak anapara tahsisi yapmak için bir fonksiyon geliştirdim:

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

Bu fonksiyon, anaparayı daha az riskli döviz pariteleri lehine otomatik olarak yeniden tahsis etmemize olanak tanır ve bu da tüm portföyün daha dengeli bir risk yönetimine katkıda bulunur.

VaR korelasyon matrisi. Döviz pariteleri arasındaki ilişkileri dikkate almak için VaR korelasyon matrisinin hesaplanmasını uyguladım:

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

Bu matris, genel portföy riskinin daha doğru bir şekilde değerlendirilmesine ve döviz pariteleri arasındaki aşırı korelasyonla ilgili potansiyel sorunların belirlenmesine olanak tanır. Ayrıca, her bir döviz paritesinin özelliklerini dikkate almak için grid parametresi ayarlama fonksiyonunu da değiştirdim:

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
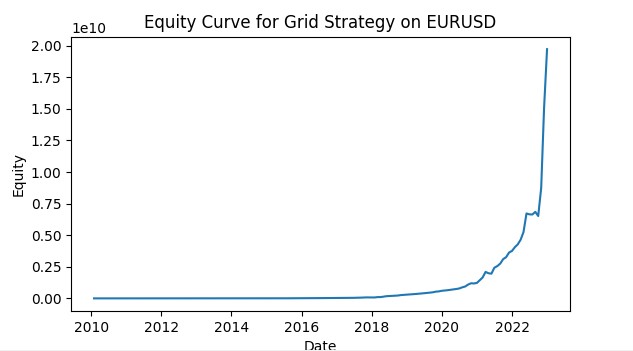
    return adjusted_params

Bu, her bir gridin kendi döviz paritesinin mevcut koşullarına uyum sağlamasına olanak tanıyarak stratejinin genel verimliliğini artırır. İşte VaR kullanan bir grid alım-satım simülasyonunun ekran görüntüsü. Sistemi, VaR konseptine göre riskleri kontrol etmek için makine öğrenimi modellerini ve olası fiyat hareketlerini tahmin etmek için modelleri kullanacak ve bir emir gridi ile birleşecek tam teşekküllü bir alım-satım robotuna dönüştürmeyi planlıyorum. Sonuçları gelecek makalelerde ele alacağız.

Sonuç

Riski yönetmek için VaR kullanma gibi basit bir fikirle yola çıktığımda, bunun beni nereye götüreceği hakkında hiçbir fikrim yoktu. Temel denklemlerden karmaşık çok boyutlu modellere, tek işlemlerden çok dövizli portföyleri dinamik olarak uyarlamaya kadar her adım yeni ufuklar ve yeni zorluklar açtı.

Bu deneyimden ne öğrendim? Birincisi, VaR gerçekten güçlü bir araçtır, ancak her araç gibi doğru kullanılması gerekir. Sayılara körü körüne güvenemezsiniz. Bunun yerine, her zaman piyasayı takip etmeniz ve beklenmedik durumlara karşı hazırlıklı olmanız gerekir.

İkinci olarak, VaR'ı alım-satım sistemlerine entegre etmek sadece başka bir ölçüt eklemekle ilgili değildir. Bu, risk ve anapara yönetimi yaklaşımının tamamen yeniden düşünülmesi anlamına gelmektedir. Alım-satım işlemlerim daha bilinçli ve daha yapılandırılmış hale geldi. 

Üçüncüsü, çok dövizli stratejilerle çalışmak benim için alım-satımda yeni bir boyut açtı. Korelasyonlar, karşılıklı bağımlılıklar, dinamik anapara tahsisi - tüm bunlar inanılmaz derecede karmaşık ama aynı zamanda inanılmaz derecede ilginç bir bulmaca oluşturuyor. Ve VaR bunu çözmenin anahtarıdır.

Elbette çalışmalar henüz bitmiş değil. Makine öğreniminin VaR tahminine nasıl uygulanacağı ve dağılımın "kalın kuyruklarını" daha iyi hesaba katmak için doğrusal olmayan modellerin nasıl entegre edileceği konusunda halihazırda fikirlerim var. Forex asla yerinde durmaz ve modellerimiz de onunla birlikte gelişmelidir.