スワップ(第I部)：ロックと合成ポジション

MetaTrader 5 — トレーディング | 6 9月 2021, 10:05

543

はじめに

本稿のトピックについては長い間考えていたのですが、詳細な調査を行う時間がありませんでした。スワップのトピックは、主にすべてのピップを数えるプロトレーダーの間で、Web上で非常に広まっています。これは、実際には取引への最良のアプローチです。本稿から、スワップを有効に使用する方法とともにスワップを常に考慮に入れる必要があることがわかるでしょう。また、本稿ではスワップ取引手法を最新化する方法について、非常に複雑ではあるが興味深いアイデアを取り上げています。このような手法(適切に準備されている場合)は、1つの口座内で使用することも、2つの口座を使用する従来のロックの利益向上ツールとして使用することもできます。

スワップについて

スワップの概念とその理論については説明しません。私が興味があるのはスワップの実用化のみです。最も重要な問題は、スワップを介して利益を生み出すことが可能かどうかです。トレーダーの観点からは、スワップは利益または損失です。さらに、多くのトレーダーは、日中の取引に固執しており、単にスワップを無視します。スワップが取引にほとんど影響を与えるほど重要ではないと考えて、スワップに注意を払わないトレーダーもいます。実際、スプレッドのほぼ半分はスワップに隠されている可能性があります。このスプレッドは、売買時ではなく、サーバ上で日が変わったときに発生します。

スワップは、ポジションボリュームに対して課金され、次の瞬間に発生します。

月曜日から火曜日
火曜日から水曜日
水曜日から木曜日(ほとんどすべての証券会社が水曜日の夜にトリプルスワップを請求します)
木曜日から金曜日

通常、スワップ値は、取引商品の仕様にポイントまたは割合で示されます。他の計算方法もありますが、私が理解できたのはそのうちの2つだけで、これで十分です。スワップに関する構造化された情報はほとんどありませんが、質問を研究すると、効率的なスワップベースのストラテジーが見つかる場合もあります。生み出される利益率は最小限ですが、利益は絶対に保証されるという大きな利点があります—。このアプローチの主な難しさは、最も人気のあるブローカーにはポジティブスワップのある商品がほとんどないという事実です。そのため、このアイデアからお金を稼ぐのは本当に難しいです。潜在的な利益でさえ非常に低いですが、それでも、これは預金を完全に失うよりはましです。他の取引システムを使用すれば、おそらく預金を完全に失うことになります。

外国為替取引に関する私の結論は、利益を保証できるものはポジティブスワップ以外に何もないということです。もちろん、利益を生み出すことができるシステムはいくつかあります。ただし、それらを使用する場合は、ブローカーに取引操作の代金を支払うことに同意し、価格が正しい方向に進むことを願うことになります。ポジティブスワップは逆のプロセスです。私は次のステートメントをポジティブスワップ方向の取引のマーカーと見なします。

ポジティブスワップは、ポジション(毎日の利益)に向けた部分的な価格変動に相当します。
しばらくすると、スワップはスプレッドと手数料の損失をカバーすることができます。しばらくすると、スワップで資金が追加されます。
スワップが機能するためには、ポジションをできるだけ長く保持する必要があります。そうすれば、このポジションの利益率は最大になります。
徹底的に開発された場合、利益は絶対的に予測可能であり、保証されます。

もちろん、このアプローチの最大の欠点は預金への依存ですが、他の概念は外国為替の利益をそれほど自信を持って保証することができません。この依存関係は、ポジションまたはリスクの量(これは同じです)を減らすことで減らすことができます。リスクは、ポジションボリュームと預金の比率です。ポジションボリュームの増加は、価格が負ける方向に進む可能性があり、スプレッドと手数料からの損失を補うためにスワップからの利益を待つのに預金が十分でない可能性があるというリスクを高めます。起こりうるすべての悪影響の影響を最小限に抑えるために、ロック機構が発明されました。

2つの取引口座を使用したロック

このスワップ取引手法は、トレーダーの間で最も人気があります。このストラテジーを実装するには、同じ通貨ペアまたは他の資産に対して異なるスワップを持つ2つの口座が必要になります。同じ口座内で2つの反対のポジションを開くことは無意味で、単に預金を失うことと同じです。銘柄にポジティブスワップがある場合でも、反対方向に取引するとこのスワップはネガティブになります。次の図は、この方法の概念を反映しています。

古典的なスワップ取引

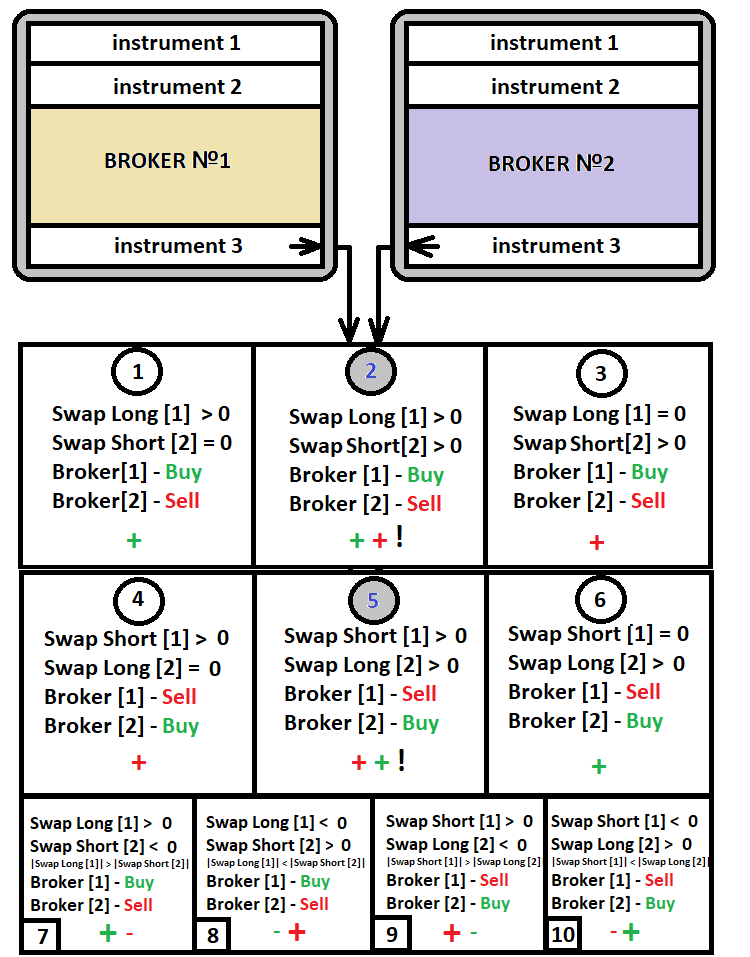
図からわかるように、スワップを取引したい特別に選択された商品の取引シナリオは10しかなく、そのうち6つが積極的に使用されています。ここでのスワップの1つがネガティブであるため、条件「1〜6」に一致する通貨ペアを見つけることが不可能な場合は、最後の4つのオプションを最後の手段として選択できます。利益はネガティブスワップよりも大きいポジティブスワップから得ることができます。さまざまなブローカーとそのスワップテーブルを分析すると、上記のすべてのケースを見つけることができます。ただし、このストラテジーに最適なオプションは「2」と「5」です。これらのオプションには両端にポジティブスワップがあるため、したがって、利益は両方のブローカーから得られます。さらに、口座間で頻繁に資金を移動する必要はありません。

このストラテジーの主な欠点は、口座間で資金を移動する必要があることです。反対のポジションを開くと、あるブローカーで損失が発生して別のブローカーで利益が発生するためです。ただし、既存の預金との関係で取引量を正しく計算すれば、資金を頻繁に移動する必要はありません。しかし、議論の余地のない利点が1つあります。利益の正確なサイズは予測できませんが、いずれにせよ、利益があるということです。多くのユーザーは、このルーチンを避けて、どうにか1つの口座内でこれらの操作を実行することを好むと思いますが、これは不可能です。ただし、1つの口座内での取引が許可されていない場合でも、従来のスワップ取引方法の利益を増やす方法は1つあります。この方法の主な機能について説明しましょう。

為替レートについて

すべてのロジックが構築される基準から始めましょう。これに基づいて数式を作成できます。例としてEURUSD、USDJPY、EURJPYについて考えてみます。これら3つのペアはすべて相関しています。関係を理解するために、これらの銘柄を少し異なる形式で提示しましょう。

1/P = EUR/USD
1/P = USD/JPY
1/P = EUR/JPY
Pは、選択した通貨のレートです。

すべての取引商品には、私たちが取得する通貨(または同等の資産)と、その代わりに提供する別の通貨があります。たとえば、最初の比率(EURUSDペア)を取得した場合、1ロットの買いポジションを開くと、10万単位の基本通貨を取得します。これは外国為替取引ルールで、1ロットは常に基本通貨の10万単位に等しいです。このペアの基本通貨はEURであるため、EURをUSDで購入します。この場合の為替レート「P」は、1ユーロに含まれる米ドルの単位数を意味します。同じことが他のすべての銘柄にも当てはまります。基本通貨は分子に含まれ、分母は「主通貨」です(この命名に賛成できない方は、以下にコメントを追加してください) 。主通貨の金額は、価格にEUR値を掛けるだけで計算されます。

1/P = EUR/USD ---> USD/P = EUR ---> USD = P*EUR
EUR = Lots*100000

売りポジションを開くと、通貨の場所が交換します。基本通貨が主通貨として機能し始め、主通貨が基本通貨になります。つまり、米ドルをユーロで購入しますが、両方の通貨の金額は、ユーロに対して同じ方法で計算されます。これは正しいです。そうしないと、かなり多くの混乱が生じるからです。計算は他の通貨でも同じです。したがって、さらなる計算では、基本通貨に記号「+」と主通貨に記号「-」を使用します。その結果、どの取引にも、私たちが何を何のために購入するかを象徴する2つの対応する数字のセットがあります。これの別の解釈は、製品として機能する通貨と、通貨として機能し、製品を購入するために支払う別の通貨が常に存在するということです。

複数の商品に対して複数のポジションを開くと、より多くの主要通貨と追加通貨が存在するため、一種の総合的なポジションになります。スワップを使用するという観点からは、このような総合的なポジションはまったく役に立ちません。しかし、非常に役立つような合成ポジションを作成することはできます。少し後でお見せします。2つの通貨で表されるボリュームの計算を決定しました。これに基づいて、より単純なものと同等の複雑な合成ポジションを作成できると結論付けることができます。

EUR/JPY = EUR/USD * USD/JPY - 2つのデリバティブで構成される為替レート

実際には、そのようなレートは無数にあり、次のようないくつかの通貨で構成されています。

EUR - 欧州連合ユーロ
USD - 米ドル
JPY - 日本円
GBP - 英国ポンド
CHF - スイスフラン
CAD - カナダドル
NZD - ニュージーランドドル
AUD - オーストラリアドル
CNY - 人民元
SGD - シンガポールドル
NOK - ノルウェークローネ
SEK - スウェーデンクローナ

これは通貨の完全なリストではありません。知っておく必要があるのは、任意の取引商品はこのリストの任意の通貨で構成できるということです。これらの取引商品のいくつかはブローカーによって提供されますが、他の商品のポジションの組み合わせとして取得できるものもあります。典型的な例はEURJPYペアです。これはデリバティブ為替レートを構成する最も単純な例ですが、これらのアイデアに基づいて、任意のポジションを他の商品のポジションのセットとして提示できると結論付けることができます。上記によると、次のことがわかります。

Value1は、絶対値で表される基本銘柄通貨です。
Value2は、絶対値で表される追加の銘柄通貨です。
Aはポジションの基本通貨のロットボリュームです。
Bはポジションの主要通貨のロットボリュームです。
Contractは絶対値での購入または販売された通貨の金額です(1ロットに対応)。
A = 1/P = Value1/Value2 - これは任意の取引商品の方程式です(気配値表示ウィンドウに表示されていないものを含む)。
Value1 = Contract*A
Value2 = Contract*B

後でロットを計算するためにこれらの比率が必要になります。今のところは覚えておいてください。これらの比率は、売買される通貨の数の比率を表します。これに基づいて、より深刻なコードロジックを構築できます。

合成ポジションを使用したロック

本稿では、合成ポジションは他のいくつかのポジションから構成できるポジションですが、これらの他のポジションは必ず他の商品で構成されている必要があります。このポジションは、すべての商品について1つのポジションに相当する必要があります。複雑に思えますが、実際は非常に簡単です。このようなポジションは、次の目的で必要になる場合があります。

シミュレートされた取引商品の元のポジションをロックする
ポジションに相当するスワップレートが完全に異なるポジションの作成を試みる
その他の目的

もともと、私はポイント2に関連してこのアイデアを思いつきました。ブローカーはさまざまな目的でスワップ値を設定しますが、その主な目的は追加の利益を生み出したいという願望です。ブローカーは、トレーダーがスワップを過度に取引することを防ぐために、競合他社のスワップも考慮に入れていると思います。次の図は、この概念を説明しています。おそらく、この図は改善できるでしょう。

この手法の一般的なスキームは次のとおりです。

メソッド図

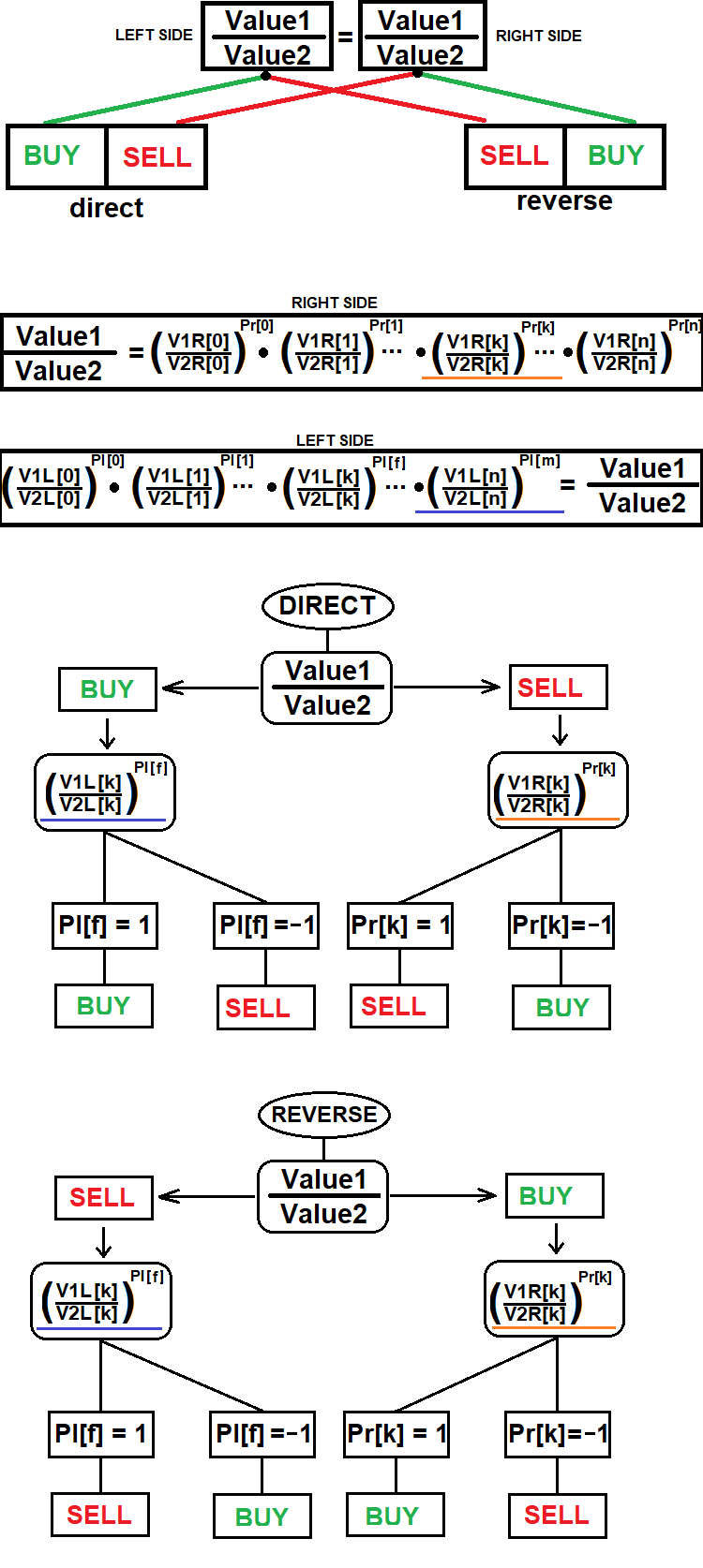
このスキームでさえ、合成ポジションを開く方法に関する完全なデータをカバーしていません。この図は、合成ポジションの特定のコンポーネントの取引方向を決定する方法のみを示しています。これは、選択したブローカーの利用可能な商品の1つによって必ず表される必要があります。

次に、これらのポジションのボリュームを計算する方法を決定する必要があります。論理的には、ボリュームは、ポジションが結果の機器の1ロットの位置と同等である必要があるという考慮に基づいて計算する必要があります。このポジションには、選択した方程式の変形が削減されます。ボリュームの計算には、次の値が必要です。

ContractB - 方程式が縮小されるペアの契約サイズ(ほとんどの場合、基本通貨の100,000単位に等しい)
Contract[1] - ロットを決定するペアの契約サイズ
A [1] - 前のバランスの取れたペア(またはチェーンの最初)のロットで表された基本通貨の金額
B [1] - 前のバランスの取れたペア(またはチェーンの最初)のロットで表された主要通貨の金額
A[2] - 現在のバランスが取れているペアのロットで表される基本通貨の金額
B[2] - 現在のバランスが取れているペアのロットで表される主要通貨の金額
B[2] - 前のバランスの取れたペア(またはチェーンの最初のペア)の契約サイズ
C[2] - 現在のバランスの取れたペアの契約サイズ

組み合わせの結果として生じる商品がブローカーによって提供されない可能性があるため、「ContractB」を決定できるとは限らないことに注意してください。この場合、契約は任意に設定できます。たとえば、基本定数「100000」に等しくなります。

最初に、チェーンの最初のペアが決定されます。これには、目的のポジションにある結果の商品の基本通貨が含まれます。次に、他のペアが検索され、結果の同等物に含まれていない余分な通貨が補正されます。メイン通貨が現在のペアの正しいポジションにあるときに、バランシングは終了します。これがどのように行われるかを示す図を作成しました。

正規化

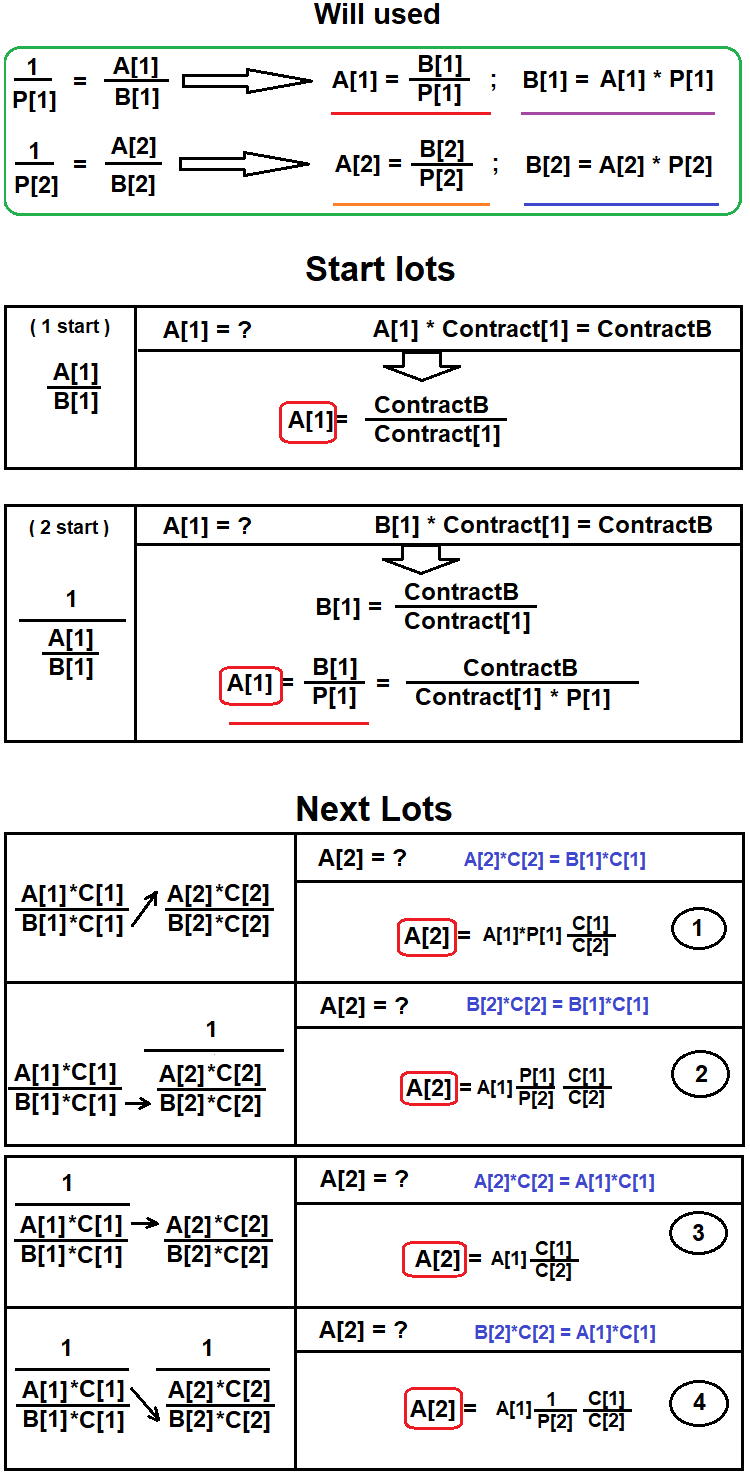
次に、これらの手法をコードに実装して、結果を分析しましょう。最初のプロトタイプは、アイデアの正しさを評価することが唯一の目的であるため、非常に単純です。上記の図が、アイデアのすべての詳細を理解するのに役立つことを願っています。

スワップポリゴンを調べるユーティリティの作成

気配値表示の並べ替えとデータの準備:

この手法を使用するには、名前が正確に6文字で、大文字のみで構成されているペアのみを選択する必要があります。私はすべてのブローカーがこの命名規則を順守していると思います。一部のブローカーはプレフィックスまたはポストフィックスを追加します。これらは、文字列データを操作するためのアルゴリズムを作成するときにも考慮する必要があります。銘柄情報を便利な形式で保存するために、2つの構造を作成しました(2番目の構造は後で使用します)。

struct Pair// required symbol information
   {
   string Name;// currency pair
   double SwapBuy;// buy swap
   double SwapSell;// sell swap
   double TickValue;// profit from 1 movement tick of a 1-lot position
   double TickSize;// tick size in the price
   double PointX;// point size in the price
   double ContractSize;// contract size in the base deposit currency
   double Margin;// margin for opening 1 lot
   };

struct PairAdvanced : Pair// extended container
   {
   string Side;// in numerator or denominator
   double LotK;// lot coefficient
   double Lot;// lot
   };

一部のフィールドは、ペアを並べ替えるときに使用されません。不要なコンテナを作らないように少し拡張して、他の用途にも使えるようにしました。同様のアルゴリズムのプロトタイプはありましたが、機能が非常に限られており、メインターミナルウィンドウにあるペアしか考慮できませんでした。今では、すべてが簡単になりました。さらに重要なのは、すべての操作がアルゴリズムで自動化されていることです。商品で配列のサイズを設定するには、次の関数が必要です。

Pair Pairs[];// data of currency pairs
void SetSizePairsArray()// set size of the array of pairs
   {
   ArrayResize(Pairs,MaxSymbols);
   ArrayResize(BasicPairsLeft,MaxPairs*2); // since each pair has 2 currencies, there can be a maximum of 2 times more base currencies
   ArrayResize(BasicPairsRight,MaxPairs*2);// since each pair has 2 currencies, there can be a maximum of 2 times more base currencies
   }

最初の行は、使用できる気配値表示ウィンドウのペアの最大数を設定します。他の2行は、使用される配列のサイズを設定します。残りの2つの配列は補助的な役割を果たします。通貨ペアを2つの部分(2つの複合通貨)に分割することができます。黄色で強調表示されている変数は、EAの入力パラメータです。

MaxSymbols - 最大ペアストレージサイズ(手動仕様を実装しました)
MaxPairs - 生成する数式の両方の部分のペアの最大数(この数より長い数式はエキスパートアドバイザーによって検索されません)

取引商品が基準(他の商品に存在する可能性のある2つの異なる通貨の兆候)を満たしているかどうかを確認するために、次の述語関数を作成しました。

bool IsValid(string s)// checking the instrument validity (its name must consist of upper-case letters)
   {
   string Mask="abcdefghijklmnopqrstuvwxyz1234567890";// mask of unsupported characters (lowercase letters and numbers)
   for ( int i=0; i<StringLen(s); i++ )// reset symbols
      {
      for ( int j=0; j<StringLen(Mask); j++ )
         {
         if ( s[i] == Mask[j] ) return false;
         }
      }   
   return true;
   }

この機能は、商品の将来のチェックの唯一の条件ではありません。ただし、この条件は論理式内に記述できないため、述語として実装する方が簡単です。次に、配列に必要なデータを入力するmain関数に移りましょう。

void FillPairsArray()// fill the array with required information about the instruments
   {
   int iterator=0;
   double correction;
   int TempSwapMode;
   
   for ( int i=0; i<ArraySize(Pairs); i++ )// reset symbols
      {
      Pairs[iterator].Name="";
      }   
   
   for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window
      {
      TempSwapMode=int(SymbolInfoInteger(Pairs[iterator].Name,SYMBOL_SWAP_MODE));
      if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) && SymbolInfoInteger(SymbolName(i,false),SYMBOL_TRADE_MODE) == SYMBOL_TRADE_MODE_FULL  
      && ( ( TempSwapMode  == 1 )  ||  ( ( TempSwapMode == 5 || TempSwapMode == 6 ) && CorrectedValue(Pairs[iterator].Name,correction) )) )
         {
         if ( iterator >= ArraySize(Pairs) ) break;
         Pairs[iterator].Name=SymbolName(i,false);
         Pairs[iterator].TickSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_SIZE);
         Pairs[iterator].PointX=SymbolInfoDouble(Pairs[iterator].Name, SYMBOL_POINT);
         Pairs[iterator].ContractSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_CONTRACT_SIZE);
         switch(TempSwapMode)
           {
            case  1:// in points
              Pairs[iterator].SwapBuy=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize);
              Pairs[iterator].SwapSell=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize);              
              break;
            case  5:// in percent
              Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);
              Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);              
              break;
            case  6:// in percent
              Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);
              Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);              
              break;              
           }     
         Pairs[iterator].Margin=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_MARGIN_INITIAL);
         Pairs[iterator].TickValue=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_VALUE);         
         iterator++;
         }
      }
   }

この関数は、すべての銘柄の単純な反復と、文字列名の長さの要件への準拠とこの銘柄の取引の可能性の両方を確認する複雑な複合条件によるフィルタリング、およびスワップの対象となる銘柄に関連する他のパラメータを提供します。計算方法は、「in points」で最も一般的に使用される方法とは異なります。「switch」ブロックでスワップ計算方法の1つが選択されます。現在、ポイントと割合の2つの方法が実装されています。適切な並び替えは、不必要な計算を避けるために主に重要です。また、赤で強調表示されている関数にもご注意ください。主通貨(基本通貨ではない)が預金通貨と一致しない通貨で表されている場合、特定の調整係数を追加して、預金通貨への秘密のスワップを行う必要があります。この関数は、関連する値を計算します。そのコードは次のとおりです。

bool CorrectedValue(string Pair0,double &rez)// adjustment factor to convert to deposit currency for the percentage swap calculation method
   {
   string OurValue=AccountInfoString(ACCOUNT_CURRENCY);// deposit currency
   string Half2Source=StringSubstr(Pair0,PrefixE+3,3);// lower currency of the pair to be adjusted
   if ( Half2Source == OurValue )
      {
      rez=1.0;
      return true;
      }
   
   for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window
      {
      if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) )//find the currency rate to convert to the account currency
         {
         string Half1=StringSubstr(SymbolName(i,false),PrefixE,3);
         string Half2=StringSubstr(SymbolName(i,false),PrefixE+3,3);
     
         if ( Half2 == OurValue && Half1 == Half2Source )
            {
            rez=SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID);
            return true;
            }
         if ( Half1 == OurValue && Half2 == Half2Source )
            {
            rez=1.0/SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID);
            return true;
            }            
         }
      } 
   return false;
   }

この関数は述語として機能するだけでなく、参照によって外部から渡された変数に調整係数の値を返します。調整係数は、預金通貨を含む希望通貨のレートに基づいて計算されます。

ランダムに生成された数式

アレイに必要なデータが入力されているとします。次に、どうにかこれらの銘柄を繰り返し処理し、これらのペアから作成できる数式のすべての可能な組み合わせをその場で作成する必要があります。まず、数式を保存する形式を決定する必要があります。この式のすべての要素を格納する構造は、ログを表示する必要がある場合に備えて、ユーザーにとって非常にシンプルで明確である必要があります(ただし、そのような必要性は確実にあります。そうでない場合、エラーを特定できません)。

式は、「=」記号の左側と右側の両方にある一連の要素です。係数は、1または-1の累乗の通貨レートにすることができます(これは、逆の分数、または現在の商品レートを参照する単位に相当します)。次の構造体を使用することにしました。

struct EquationBasic // structure containing the basic formula
   {
   string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign
   string LeftSideStructure;// structure of the left side of the formula
   string RightSide;// currency pairs participating in the right side of the formula
   string RightSideStructure;// structure of the right side of the formula
   };

すべてのデータは文字列形式で保存されます。式を調べるために、これらの文字列を解析して、必要なすべての情報を抽出します。また、必要なときにいつでも印刷できます。生成された数式は、次の形式で出力されます。

ランダム方程式

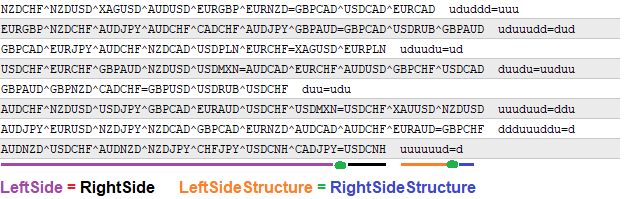
私個人としては、そのような記録は絶対に明確で読みやすいものです。文字^は、ペア間の区切り文字として使用されます。乗数の次数を示すuとdの単一文字で構成されているため、数式構造には、区切り文字は必要ありません。

「u」は為替レートです
「d」は1 /通貨レートです

ご覧のとおり、結果の数式には、方程式の両側の浮動長と浮動サイズがありますが、このサイズには制限があります。このアプローチは、生成された数式の最大の変動性を提供します。これにより、選択したブローカーの取引条件内で見つかったバリアントの可能な限り最高の品質が提供されます。ブローカーは完全に異なる条件を提供します。これらの数式を正常に生成するには、必要な範囲の数値を生成できる追加のランダム関数が必要です。この目的のために、組み込みのMathRand関数の機能を使用して関連する機能を作成しましょう。

int GenerateRandomQuantityLeftSide()// generate a random number of pairs on the left side of the formula
   {
   int RandomQuantityLeftSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-1)));
   if ( RandomQuantityLeftSide >= MaxPairs ) return MaxPairs-1;
   return RandomQuantityLeftSide;
   }

int GenerateRandomQuantityRightSide(int LeftLenght)// generate a random number of pairs on the right side of the formula (taking into account the number of pairs on the left side)
   {
   int RandomQuantityRightSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-LeftLenght)));
   if ( RandomQuantityRightSide < 2 && LeftLenght == 1 ) return 2;// there must be at least 2 pairs in one of the sides, otherwise it will be equivalent to opening two opposite positions
   if ( RandomQuantityRightSide > (MaxPairs-LeftLenght) ) return (MaxPairs-LeftLenght);
   return RandomQuantityRightSide;
   }
   
int GenerateRandomIndex()// generate a random index of a symbol from the MarketWatch window
   {
   int RandomIndex=0;
     
   while(true)
      {
      RandomIndex=int(MathFloor((double(MathRand())/32767.0) * double(MaxSymbols)) );
      if ( RandomIndex >= MaxSymbols ) RandomIndex=MaxSymbols-1;
      if ( StringLen(Pairs[RandomIndex].Name) > 0 ) return RandomIndex;
      }

   return RandomIndex;
   }

3つの関数はすべて、特定の段階で必要になります。次に、これらの式を生成する関数を作成できます。コードはますます複雑になりますが、タスクが標準ではないため、オブジェクト指向のアプローチは使用しません。私は手続き型アプローチを使用することにしました。結果として得られる手順は非常に大きくて面倒ですが、追加の機能はなく、コードの重複を避けるために、各関数は中間関数を使用せずに特定のタスクを実装します。そうしないと、タスクの詳細により、コードを理解するのがさらに難しくなります。関数は次のようになります。

EquationBasic GenerateBasicEquation()// generate both parts of the random equation
   {
   int RandomQuantityLeft=GenerateRandomQuantityLeftSide();
   int RandomQuantityRight=GenerateRandomQuantityRightSide(RandomQuantityLeft);
   string TempLeft="";
   string TempRight="";
   string TempLeftStructure="";
   string TempRightStructure="";   
   
   for ( int i=0; i<RandomQuantityLeft; i++ )
      {
      int RandomIndex=GenerateRandomIndex();
      if ( i == 0 && RandomQuantityLeft > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^";
      if ( i != 0 && (RandomQuantityLeft-i) > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^";
      if ( i == RandomQuantityLeft-1 ) TempLeft+=Pairs[RandomIndex].Name;
      
      if ( double(MathRand())/32767.0 > 0.5 ) TempLeftStructure+="u";
      else TempLeftStructure+="d";
      }
      
   for ( int i=RandomQuantityLeft; i<RandomQuantityLeft+RandomQuantityRight; i++ )
      {
      int RandomIndex=GenerateRandomIndex();
      
      if ( i == RandomQuantityLeft && RandomQuantityRight > 1 ) TempRight+=Pairs[RandomIndex].Name+"^";
      if ( i != RandomQuantityLeft && (RandomQuantityLeft+RandomQuantityRight-i) > 1 ) TempRight+=Pairs[RandomIndex].Name+"^";
      if ( i == RandomQuantityLeft+RandomQuantityRight-1 ) TempRight+=Pairs[RandomIndex].Name;
      
      if ( double(MathRand())/32767.0 > 0.5 ) TempRightStructure+="u";
      else TempRightStructure+="d";
      }
      
   EquationBasic result;
   result.LeftSide=TempLeft;
   result.LeftSideStructure=TempLeftStructure;
   result.RightSide=TempRight;
   result.RightSideStructure=TempRightStructure;
   
   return result;
   }

ご覧のとおり、ここでは、以前に検討した3つの関数すべてを使用して、ランダムな数式を生成します。これらの関数は、コード内の他の場所では使用されません。数式の準備ができたらすぐに、この数式の段階的な分析に進むことができます。不正な数式はすべて、次の非常に重要な複雑なフィルターによって破棄されます。まず、等しいかどうかを確認します。部分が等しくない場合、この式は正しくありません。準拠するすべての式は、次の分析ステップに進みます。

式バランシング

このステップでは、一度に複数の分析基準を対象とします。

分子と分母のすべての余分な要素を数えて削除します
分子に1つの通貨、分母に1つの通貨が利用可能かどうかを確認します
得られた分数の左側と右側の対応を確認します
右側が左側の逆数である場合、式の右側の構造を単純に逆にします(これは「-1」の累乗に似ています)
すべてのステージが正常に完了すると、結果が新しい変数に書き込まれます

これらの手順がコードにどのように表示されるかを次に示します。

BasicValue BasicPairsLeft[];// array of base pairs to the left
BasicValue BasicPairsRight[];// array of base pairs to the right
bool bBalanced(EquationBasic &CheckedPair,EquationCorrected &r)// if the current formula is balanced (if yes, return the corrected version to the "r" variable)
   {
   bool bEnd=false;
   string SubPair;// the full name of the currency pair
   string Half1;// the first currency of the pair
   string Half2;// the second currency of the pair
   string SubSide;// the currency pair in the numerator or denominator
   string Divider;// separator
   int ReadStartIterator=0;// reading start index
   int quantityiterator=0;// quantity
   bool bNew;
   BasicValue b0;
   
   for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs 
      {
      BasicPairsLeft[i].Value = "";
      BasicPairsLeft[i].Quantity = 0;
      }
   for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs
      {
      BasicPairsRight[i].Value = "";
      BasicPairsRight[i].Quantity = 0;
      }
   //// Calculate balance values for the left side
   quantityiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(CheckedPair.LeftSide); i++ )// extract base currencies from the left side of the equation
      {
      Divider=StringSubstr(CheckedPair.LeftSide,i,1);
      if ( Divider == "^" || i == StringLen(CheckedPair.LeftSide) - 1 )
         {
         SubPair=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,6);
         SubSide=StringSubstr(CheckedPair.LeftSideStructure,quantityiterator,1);
         Half1=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,3);
         Half2=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE+3,3);         

         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsLeft[j].Value == Half1 )
               {
               if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
               if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
               {
               if ( StringLen(BasicPairsLeft[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
                  if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;                  
                  BasicPairsLeft[j].Value=Half1;
                  break;
                  }
               }            
            }
            
         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsLeft[j].Value == Half2 )
               {
               if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
               if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
               {
               if (  StringLen(BasicPairsLeft[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
                  if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;                  
                  BasicPairsLeft[j].Value=Half2;
                  break;
                  }
               }            
            }            
                  
         ReadStartIterator=i+1;
         quantityiterator++;
         }
      }
   /// end of left-side balance calculation
      
   //// Calculate balance values for the right side
   quantityiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(CheckedPair.RightSide); i++ )// extract base currencies from the right side of the equation
      {
      Divider=StringSubstr(CheckedPair.RightSide,i,1);

      if ( Divider == "^"|| i == StringLen(CheckedPair.RightSide) - 1 )
         {
         SubPair=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,6);
         SubSide=StringSubstr(CheckedPair.RightSideStructure,quantityiterator,1);
         Half1=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,3);
         Half2=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE+3,3);         

         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsRight[j].Value == Half1 )
               {
               if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
               if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
               {
               if (  StringLen(BasicPairsRight[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
                  if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;                  
                  BasicPairsRight[j].Value=Half1;
                  break;
                  }
               }            
            }
            
         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsRight[j].Value == Half2 )
               {
               if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
               if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
               {
               if (  StringLen(BasicPairsRight[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
                  if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;                  
                  BasicPairsRight[j].Value=Half2;
                  break;
                  }
               }            
            }            
                  
         ReadStartIterator=i+1;
         quantityiterator++;
         }
      }
   /// end of right-side balance calculation
 
   /// calculate the number of lower and upper currencies based on the received data from the previous block
   int LeftUpTotal=0;// the number of upper elements in the left part
   int LeftDownTotal=0;// the number of lower elements in the left part
   int RightUpTotal=0;// the number of upper elements in the right part
   int RightDownTotal=0;// the number of lower elements in the right part
   
   
   string LastUpLeft;
   string LastDownLeft;
   string LastUpRight;
   string LastDownRight;   
   for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )
      {
      if ( BasicPairsLeft[i].Quantity > 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[i].Quantity;
      if ( BasicPairsLeft[i].Quantity < 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[i].Quantity;
      }
   for ( int i=0; i<ArraySize(BasicPairsRight); i++ )
      {
      if ( BasicPairsRight[i].Quantity > 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightUpTotal+=BasicPairsRight[i].Quantity;
      if ( BasicPairsRight[i].Quantity < 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightDownTotal-=BasicPairsRight[i].Quantity;
      }      
   ///
   /// check if both sides are equal
   if ( LeftUpTotal == 1 && LeftDownTotal == 1 && RightUpTotal == 1 && RightDownTotal == 1 )// there must be one pair in the upper and in the lower part of both sides of the equality, otherwise the formula is invalid
      {
      for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )
         {
         if ( BasicPairsLeft[i].Quantity == 1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastUpLeft=BasicPairsLeft[i].Value;
         if ( BasicPairsLeft[i].Quantity == -1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastDownLeft=BasicPairsLeft[i].Value;
         }
      for ( int i=0; i<ArraySize(BasicPairsRight); i++ )
         {
         if ( BasicPairsRight[i].Quantity == 1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastUpRight=BasicPairsRight[i].Value;
         if ( BasicPairsRight[i].Quantity == -1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastDownRight=BasicPairsRight[i].Value;
         }      
      }
   else return false;
   if ( (LastUpLeft == LastUpRight && LastDownLeft == LastDownRight) || (LastUpLeft == LastDownRight && LastDownLeft == LastUpRight) )
      {
      if ( LastUpLeft == LastDownRight && LastDownLeft == LastUpRight )// If the formula is cross-equivalent, then invert the structure of the right part of the equation (it is the same as raising to the power of -1)
         {
         string NewStructure;// the new structure that will be built from the previous one
         for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ )
            {
            if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d";
            if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u";
            }
         CheckedPair.RightSideStructure=NewStructure;
         }      
      }
   else return false;// if the resulting fractions on both sides are not equivalent, then the formula is invalid
   if ( LastUpLeft == LastDownLeft ) return false;// if result in one, then the formula is invalid

  /// Now it is necessary to write all the above into a corrected and more convenient structure
   string TempResult=CorrectedResultInstrument(LastUpLeft+LastDownLeft,r.IsResultInstrument);
   if ( r.IsResultInstrument && LastUpLeft+LastDownLeft != TempResult ) 
      {
      string NewStructure="";// the new structure that will be built from the previous one
      for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ )
         {
         if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d";
         if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u";
         }
      CheckedPair.RightSideStructure=NewStructure;
      NewStructure="";// the new structure that will be built from the previous one
      for ( int i=0; i<StringLen(CheckedPair.LeftSideStructure); i++ )
         {
         if ( CheckedPair.LeftSideStructure[i] == 'u' ) NewStructure+="d";
         if ( CheckedPair.LeftSideStructure[i] == 'd' ) NewStructure+="u";
         }
      CheckedPair.LeftSideStructure=NewStructure;      
        
      r.ResultInstrument=LastDownLeft+LastUpLeft;
      r.UpPair=LastDownLeft;
      r.DownPair=LastUpLeft;      
      }
   else
      {
      r.ResultInstrument=LastUpLeft+LastDownLeft;
      r.UpPair=LastUpLeft;
      r.DownPair=LastDownLeft;
      }

   r.LeftSide=CheckedPair.LeftSide;
   r.RightSide=CheckedPair.RightSide;
   r.LeftSideStructure=CheckedPair.LeftSideStructure;
   r.RightSideStructure=CheckedPair.RightSideStructure;
   ///   
    
   /// if code has reached this point, it is considered that we have found the formula meeting the criteria, and the next step is normalization
      
   return true;
   }

銘柄のリストに数式が縮小されたものが含まれているかどうかを判断するには、緑色で強調表示されている関数が必要です。たとえば、「USDJPY」ではなく「JPYUSD」に数式が縮小されていることが判明する場合があります。そのような銘柄は、作成できたとしても、明らかに存在しません。ただし、ここでやるべきことは、正しい取引商品を生み出すように公式を修正することです。この場合、数式の両方の部分を-1の累乗にする必要があります。これは、数式の構造を逆にすることと同じです(「d」を「u」に、またはその逆に変更します)。気配値表示ウィンドウにそのような銘柄がない場合は、そのままにしておきます。

string CorrectedResultInstrument(string instrument, bool &bResult)// if any equivalent symbol corresponds to the generated formula, return this symbol (or leave as is)
   {   
   string Half1="";
   string Half2="";   
   string Half1input=StringSubstr(instrument,0,3);//input upper currency
   string Half2input=StringSubstr(instrument,3,3);//input lower currency
   bResult=false;
   for ( int j=0; j<ArraySize(Pairs); j++ )
      {
      Half1=StringSubstr(Pairs[j].Name,PrefixE,3);
      Half2=StringSubstr(Pairs[j].Name,PrefixE+3,3);
      if ( (Half1==Half1input && Half2==Half2input) || (Half1==Half2input && Half2==Half1input) )// direct match or crossed match
         {
         bResult=true;
         return Pairs[j].Name;
         }
      }
   
   return instrument;
   }

フィルタを通過した数式を格納するために、次の構造体を用意しました。この構造体には、いくつかの前の構造体のからのフィールドといくつかの新しいフィールドがあります。

struct EquationCorrected // corrected structure of the basic formula
   {
   string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign
   string LeftSideStructure;// structure of the left side of the formula
   string RightSide;// currency pairs participating in the right side of the formula
   string RightSideStructure;// structure of the right side of the formula
   
   string ResultInstrument;// the resulting instrument to which both parts of the formula come after transformation
   bool IsResultInstrument;// has the suitable equivalent symbol been found
   string UpPair;// the upper currency of the resulting instrument
   string DownPair;// the lower currency of the resulting instrument
   };

数式の正規化

この手順は、結果をフィルタリングする次のステップです。これは、次の順次操作で構成され、連続しています。

方程式の両側から得られた結果の銘柄に基づいて、等式の両側のリストから開始ペアを選択します。
両方のペアは、方程式での冪乗に従って、分子で基本通貨を提供する必要があります。
そのようなペアが見つかり、分母の通貨に結果の商品の主通貨が含まれていない場合は、さらに進みます。
さらに、次のペアの分子の通貨が前のペアの分母の通貨を補うようにします。
目的のペアが見つかるまで、これらの手順を繰り返します。
結果のペアが見つかると、数式の未使用のコンポーネントはすべて破棄されます(それらの積は1であるため)。
このプロセスと並行して、「ロットファクター」はペアからペアへと順番に計算されます(結果として得られる商品を確実にするために、特定のペアのポジションを開くために必要なロットを示します)。
結果は新しい変数に書き込まれ、次の分析段階で使用されます。

関数のコードは次のとおりです。

bool bNormalized(EquationCorrected &d,EquationNormalized &v)// formula normalization attempt (the normalized formula is returned in "v" )
   {
   double PreviousContract;// previous contract
   bool bWasPairs;// if any pairs have been found
   double BaseContract;// contract of the pair to which the equation is reduced
   double PreviousLotK=0.0;// previous LotK
   double LotK;// current LotK
   string PreviousSubSide;// in numerator or denominator (previous factor)
   string PreviousPair;// previous pair
   string PreviousHalf1;// upper currency of the previous pair
   string PreviousHalf2;// lower currency of the previous pair
   string SubPair;// the full name of the currency pair
   string Half1;// the first currency of the pair
   string Half2;// the second currency of the pair
   string SubSide;// the currency pair in the numerator or denominator
   string Divider;// separator
   int ReadStartIterator=0;// reading start index
   int quantityiterator=0;// quantity
   int tryiterator=0;// the number of balancing attempts
   int quantityleft=0;// the number of pairs on the left after normalization
   int quantityright=0;//the number of pairs on the right after normalization
   bool bNew;
   BasicValue b0;
   
   for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs 
      {
      BasicPairsLeft[i].Value = "";
      BasicPairsLeft[i].Quantity = 0;
      }
   for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs
      {
      BasicPairsRight[i].Value = "";
      BasicPairsRight[i].Quantity = 0;
      }
      
   if ( d.IsResultInstrument ) BaseContract=SymbolInfoDouble(d.ResultInstrument, SYMBOL_TRADE_CONTRACT_SIZE);// define the contract of the equivalent pair based on the instrument
   else BaseContract=100000.0;
      
   //// Calculate the number of pairs for the left side
   tryiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation
      {
      Divider=StringSubstr(d.LeftSide,i,1);
      if ( Divider == "^" )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }
         
      if ( i == StringLen(d.LeftSide) - 1 )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }         
      }
   /// end of quantity calculation for the left part
      
   ArrayResize(v.PairLeft,tryiterator);
   /// calculate the lot coefficients for the left side
   
   bool bBalanced=false;// is the formula balanced
   bool bUsed[];
   ArrayResize(bUsed,tryiterator);
   ArrayFill(bUsed,0,tryiterator,false);
   int balancediterator=0;
   PreviousHalf1="";
   PreviousHalf2="";
   PreviousLotK=0.0;
   PreviousSubSide="";
   PreviousPair="";
   PreviousContract=0.0;
   bWasPairs=false;// have there been pairs
   for ( int k=0; k<tryiterator; k++ )// try to normalize the left side
      {
      if( !bBalanced )
         {
         quantityiterator=0;
         ReadStartIterator=0;
         for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation
            {
            Divider=StringSubstr(d.LeftSide,i,1);
            if ( Divider == "^" || i == StringLen(d.LeftSide) - 1 )
               {
               SubPair=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,6);
               SubSide=StringSubstr(d.LeftSideStructure,quantityiterator,1);
               Half1=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,3);
               Half2=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE+3,3);         
            
               if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list
               || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator
               || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator
                  {// find the entry point(pair) of the chain
                  if( PreviousHalf1 == "" )// define the lot coefficient of the first pair
                     {
                     if ( SubSide == "u" )
                        {
                        LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start)
                        v.PairLeft[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }
                     if ( SubSide == "d" )
                        {
                        double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                        if ( Pt == 0.0 ) return false; 
                        LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start)
                        v.PairLeft[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }                     
                     }
                  else
                     {
                     if( PreviousSubSide == "u" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false; 
                           LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 1 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false; 
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;                           
                           LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 2 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }
                     if( PreviousSubSide == "d" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           if ( PreviousContract <= 0.0 ) return false;
                           LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 3 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;
                           LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 4 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }                  
                     }
                                   
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsLeft[j].Value == Half1 )
                        {
                        if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
                        if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                        {
                        if ( StringLen(BasicPairsLeft[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
                           if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;                  
                           BasicPairsLeft[j].Value=Half1;
                           break;
                           }
                        }            
                     }
            
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsLeft[j].Value == Half2 )
                        {
                        if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
                        if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                        {
                        if (  StringLen(BasicPairsLeft[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
                           if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;                  
                           BasicPairsLeft[j].Value=Half2;
                           break;
                           }
                        }            
                     }
                  
                  v.PairLeft[balancediterator].Name=SubPair;
                  v.PairLeft[balancediterator].Side=SubSide;
                  v.PairLeft[balancediterator].ContractSize=SymbolInfoDouble(v.PairLeft[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE);
               

                  balancediterator++;                  
                  PreviousHalf1=Half1;
                  PreviousHalf2=Half2;
                  PreviousSubSide=SubSide;
                  PreviousPair=SubPair;
                  
                  quantityleft++;
                  if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted
                     {
                     bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                  if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted
                     {
                     bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                  
                  int LeftUpTotal=0;// the number of upper elements in the left part
                  int LeftDownTotal=0;// the number of lower elements in the left part
                  string LastUpLeft;
                  string LastDownLeft;
                  for ( int z=0; z<ArraySize(BasicPairsLeft); z++ )
                     {
                     if ( BasicPairsLeft[z].Quantity > 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[z].Quantity;
                     if ( BasicPairsLeft[z].Quantity < 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[z].Quantity;
                     }
                  if ( bWasPairs && LeftUpTotal == 0 && LeftDownTotal == 0 ) return false;                                           
                  }

               ReadStartIterator=i+1;
               bUsed[quantityiterator]=true;
               quantityiterator++;
               }
            }
         }
         else break;
      }
   /// end of coefficient calculation for the left part
     
   if ( !bBalanced ) return false;// if the left side is not balanced, then there is no point in balancing the right side
     
   //// Calculate the number of pairs for the right side
   tryiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation
      {
      Divider=StringSubstr(d.RightSide,i,1);
      if ( Divider == "^" )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }
         
      if ( i == StringLen(d.RightSide) - 1 )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }         
      }   
   ArrayResize(v.PairRight,tryiterator);
   /// end of calculation of the number of pairs for the right side
     
   bBalanced=false;// is the formula balanced
   ArrayResize(bUsed,tryiterator);
   ArrayFill(bUsed,0,tryiterator,false);
   balancediterator=0;
   PreviousHalf1="";
   PreviousHalf2="";
   PreviousLotK=0.0;
   PreviousSubSide="";
   PreviousPair="";
   PreviousContract=0.0;
   bWasPairs=false;
   for ( int k=0; k<tryiterator; k++ )// try to normalize the right side
      {
      if ( !bBalanced )
         {
         quantityiterator=0;
         ReadStartIterator=0;
         for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation
            {
            Divider=StringSubstr(d.RightSide,i,1);
            if ( Divider == "^" || i == StringLen(d.RightSide) - 1 )
               {
               SubPair=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,6);
               SubSide=StringSubstr(d.RightSideStructure,quantityiterator,1);
               Half1=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,3);
               Half2=StringSubstr(d.RightSide,ReadStartIterator+PrefixE+3,3);         
            
               if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list
               || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator
               || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator
                  {// find the entry point(pair) of the chain
                  if( PreviousHalf1 == "" )// define the lot coefficient of the first pair
                     {
                     if ( SubSide == "u" )
                        {
                        LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start)
                        v.PairRight[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }
                     if ( SubSide == "d" )
                        {
                        double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                        if ( Pt == 0.0 ) return false; 
                        LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start)
                        v.PairRight[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }                     
                     }
                  else
                     {
                     if( PreviousSubSide == "u" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;                            
                           LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (1)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false; 
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;                            
                           LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (2)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }
                     if( PreviousSubSide == "d" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           if ( PreviousContract <= 0.0 ) return false;
                           LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (3)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false; 
                           LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (4)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }                  
                     }                
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsRight[j].Value == Half1 )
                        {
                        if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
                        if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                        {
                        if ( StringLen(BasicPairsLeft[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
                           if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;                  
                           BasicPairsRight[j].Value=Half1;
                           break;
                           }
                        }            
                     }
            
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsRight[j].Value == Half2 )
                        {
                        if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
                        if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
                        {
                        if (  StringLen(BasicPairsRight[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
                           if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;                  
                           BasicPairsRight[j].Value=Half2;
                           break;
                           }
                        }            
                     }
                  
                  v.PairRight[balancediterator].Name=SubPair;
                  v.PairRight[balancediterator].Side=SubSide;
                  v.PairRight[balancediterator].ContractSize=SymbolInfoDouble(v.PairRight[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE);


                  balancediterator++;                  
                  PreviousHalf1=Half1;
                  PreviousHalf2=Half2;
                  PreviousSubSide=SubSide;
                  PreviousPair=SubPair;
               
                  quantityright++;
                  if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted
                     {
                     bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                  if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted
                     {
                     bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                     
                  int RightUpTotal=0;// the number of upper elements in the right part
                  int RightDownTotal=0;// the number of lower elements in the right part
                  string LastUpRight;
                  string LastDownRight; 
                    
                  for ( int z=0; z<ArraySize(BasicPairsRight); z++ )
                     {
                     if ( BasicPairsRight[z].Quantity > 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightUpTotal+=BasicPairsRight[z].Quantity;
                     if ( BasicPairsRight[z].Quantity < 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightDownTotal-=BasicPairsRight[z].Quantity;
                     }
                  if ( bWasPairs && RightUpTotal == 0 && RightDownTotal == 0 ) return false;                                       
                  }

               ReadStartIterator=i+1;
               bUsed[quantityiterator]=true;
               quantityiterator++;
               }
            }
         }
         else break;
      }     
   
   if ( quantityleft == 1 && quantityright == 1 ) return false;// if the equation has been normalized to only 2 pairs, it is not valid (at least 3 pairs are required)
      
   return bBalanced;
   }

これは非常に健全で複雑な手順ですが、コードが大幅に重複するため、このような場合は中間状態を生成しない方がよいように思われます。さらに、すべてのステージは非常にコンパクトで、論理的にブロックに分割されています。これらの関数のセットは、手書きですべての変換を実行して得られる結果に匹敵する、まったく同じ結果をもたらします。ここでは、これらすべての数学的操作は、複雑であるが必要な一連の方法によって実行されます。

見つかった式がどれほど有益であるかを理解するために、特別な分析を実行する必要があります。ペアごとに上下両方のポジションを開くことができることを忘れないでください。したがって、各式の回路には、直接と逆の2つの中間バリアントが存在する可能性があります。その結果、収益性の高い方が受け入れられます。

収益性を評価するために、スワップから生じる利益と損失で構成される利益係数と同様のメトリックを作成しました。既存の回路の発生したポジティブスワップが負のモジュラスよりも大きい場合、そのような回路は有益であると見なされます。その他の場合、そのような回路は不採算です。つまり、輪郭のスワップ係数は、1より大きい場合にのみ正になります。

返された結果は、完全に異なるコンテナに書き込まれます。このコンテナは、取引および取引ロジックのさらなる開発のための自給自足のコマンドパッケージとして作成されています。回路全体をすばやく簡単に開くために必要なすべてのものが含まれています。

struct EquationNormalized // the final structure with the formula in normalized form
   {
   Pair PairLeft[];// currency pairs on the left side
   Pair PairRight[];// currency pairs on the right side
   double SwapPlusRelative;// relative equivalent of the positive swap
   double SwapMinusRelative;// relative equivalent of the negative swap
   double SwapFactor;// resulting swap factor
   };

また、コンテンツに関する情報を便利に表示できる2つのメソッドを追加しましたが、本稿には関係がないため、ここでは提示しません。添付のソースコードでご確認ください。現在、方程式の各コンポーネントに関する情報は、配列の要素として個別に含まれています。これにより、文字列からデータを常に解析しなくても、後でデータを簡単に処理できます。おそらく、このソリューションは最初から使用できますが読みやすさを損なうことになります。

スワップ係数の計算と方程式構造の最終調整

これは、このシステムの最も重要な変数が計算される最後の段階です。バリアントは、この値に従って比較されます。値が最も高いものが最適です。

void CalculateBestVariation(EquationNormalized &ii)// calculation of the best swap factor of the formula and final structure adjustment if needed
   {
   double SwapMinus=0.0;// total negative swap
   double SwapPlus=0.0;// total positive swap
   double SwapMinusReverse=0.0;// total negative swap
   double SwapPlusReverse=0.0;// total positive swap
   
   double SwapFactor=0.0;// swap factor of the direct pass
   double SwapFactorReverse=0.0;// swap factor of the reverse pass
   
   for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// define the missing parameters for calculating the left side
      {
      for ( int j=0; j<ArraySize(Pairs); j++ )
         {
         if ( Pairs[j].Name == ii.PairLeft[i].Name )
            {
            ii.PairLeft[i].Margin=Pairs[j].Margin;
            ii.PairLeft[i].TickValue=Pairs[j].TickValue;
            ii.PairLeft[i].SwapBuy=Pairs[j].SwapBuy;
            ii.PairLeft[i].SwapSell=Pairs[j].SwapSell;
            break;
            }
         }
      }
      
   for ( int i=0; i<ArraySize(ii.PairRight); i++ )// define the missing parameters for calculating the right side
      {
      for ( int j=0; j<ArraySize(Pairs); j++ )
         {
         if ( Pairs[j].Name == ii.PairRight[i].Name )
            {
            ii.PairRight[i].Margin=Pairs[j].Margin;
            ii.PairRight[i].TickValue=Pairs[j].TickValue;
            ii.PairRight[i].SwapBuy=Pairs[j].SwapBuy;
            ii.PairRight[i].SwapSell=Pairs[j].SwapSell;
            break;
            }
         }
      }      
   
   double TempSwap;
   // calculate all components taking into account a change in the structure
   for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// for left parts
      {
      if ( ii.PairLeft[i].Side == "u" )
         {// for direct trading
         TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      if ( ii.PairLeft[i].Side == "d" )
         {// for direct trading
         TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      }
      
   for ( int i=0; i<ArraySize(ii.PairRight); i++ )// for right parts
      {
      if ( ii.PairRight[i].Side == "d" )
         {// for direct trading
         TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      if ( ii.PairRight[i].Side == "u" )
         {// for direct trading
         TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      }   
   // calculate the swap factor for the direct pass
   if ( SwapMinus > 0.0 && SwapPlus > 0.0 ) SwapFactor=SwapPlus/SwapMinus;
   if ( SwapMinus == 0.0 && SwapPlus == 0.0 ) SwapFactor=1.0;
   if ( SwapMinus == 0.0 && SwapPlus > 0.0 ) SwapFactor=1000001.0;
   if ( SwapMinus > 0.0 && SwapPlus == 0.0 ) SwapFactor=0.0;
   // calculate the swap factor for the reverse pass
   if ( SwapMinusReverse > 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=SwapPlusReverse/SwapMinusReverse;
   if ( SwapMinusReverse == 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=1.0;
   if ( SwapMinusReverse == 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=1000001.0;
   if ( SwapMinusReverse > 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=0.0;
   // select the best approach and calculate the missing values in the structure
   if ( SwapFactor > SwapFactorReverse )
      {
      ii.SwapPlusRelative=SwapPlus;
      ii.SwapMinusRelative=SwapMinus;
      ii.SwapFactor=SwapFactor;
      }
   else
      {
      ii.SwapPlusRelative=SwapPlusReverse;
      ii.SwapMinusRelative=SwapMinusReverse;
      ii.SwapFactor=SwapFactorReverse;
      bool bSigned;
      for ( int i=0; i<ArraySize(ii.PairRight); i++ )// if it is a reverse pass, then reverse the right structure of the formula
         {
         bSigned=false;
         if ( !bSigned && ii.PairRight[i].Side == "u" ) 
            {
            ii.PairRight[i].Side="d";
            bSigned=true;
            }
         if ( !bSigned && ii.PairRight[i].Side == "d" ) 
            {
            ii.PairRight[i].Side="u";
            bSigned=true;
            }
         }
      bSigned=false;    
      for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// if it is a reverse pass, then reverse the left structure of the formula
         {
         bSigned=false;
         if ( !bSigned && ii.PairLeft[i].Side == "u" ) 
            {
            ii.PairLeft[i].Side="d";
            bSigned=true;
            }
         if ( !bSigned && ii.PairLeft[i].Side == "d" ) 
            {
            ii.PairLeft[i].Side="u";
            bSigned=true;
            }
         }              
      }
      
   bool bSigned;
   for ( int i=0; i<ArraySize(ii.PairRight); i++ )// reverse the right side anyway
      {
      bSigned=false;
      if ( !bSigned && ii.PairRight[i].Side == "u" ) 
         {
         ii.PairRight[i].Side="d";
         bSigned=true;
         }
      if ( !bSigned && ii.PairRight[i].Side == "d" ) 
         {
         ii.PairRight[i].Side="u";
         bSigned=true;
         }
      }
   }

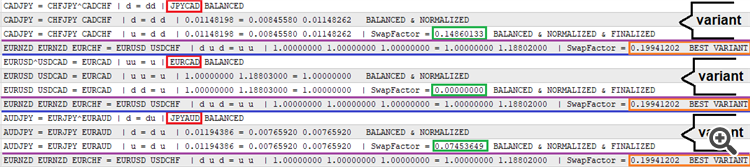
結果の順次出力を有効にするために、正常にフィルタリングされた数式バリアントが見つかった場合にのみ書き込まれるログを実装しました。ログは次のとおりです。

結果の銘柄には赤色が使用され、方程式の両辺が縮小されます。次の行は、ロット係数を使用して正規化されたバリアントを示しています。3行目は、計算されたスワップ係数を持つバリアントを示しています。4行目は、総当たり攻撃セッション中に見つかったバリアントの中で最も優れたものであり、コメント機能によってプロットされたチャートにもプロットされています。このプロトタイプは下に添付されているので、テストすることができます。実際には、スワップ取引の取引アシスタントのプロトタイプとして機能することができます。今のところ機能はほとんどありませんが、次の記事で拡張してみます。プロトタイプは、MetaTrader 4とMetaTrader 5の2つのバージョンで提供されています。

最初のテストの結論

このような複雑なトピックだけで結論を出すことは非常に困難です。それでも、これまでのところ1より大きいスワップ係数を見つけることはできませんでしたが、なんとか有用なことを理解することができました。これらは、このプロトタイプの作業を分析したときに私が得た最初の結論です。

一部の通貨ペアでは、ポジティブスワップを増やしたり、負のスワップを減らしたりすることができます(総合的な同等物としてのポジションの提示による)
収益性の高い回路が見つからない場合でも、2つの異なる取引口座をロックするために、その1部を代替ポジションとしていつでも使用できます。
このような総合的なポジションでロックすると、両端で反対のポジティブスワップが可能になるため、スワップなしの口座を使用する必要がなくなります。
機能拡張が必要な最も人気のあるブローカーを使用して、より詳細な分析を実行する必要があります。
有益なスワップファクターが達成できることを証明できることを願っています(今のところは推測にすぎません)。
賢明に使用された場合、スワップは、小さいながらも安定した利益を提供できます。

終わりに

このアプローチが興味深く、思考の糧となることを願っています。手法は理解するのが非常に難しいですが、実際には、同じボリュームで2つの反対のポジションを開くという単純な原理を実装しているものです。このような2つの反対のポジションを開くだけでは、常に損失が発生します。負の一方向スワップよりもモジュラスが大きい正の一方向スワップを提供するブローカーはありません。もちろん、数学的に不可能であるため、両方向でポジティブスワップを見つけることは決してありません。

これは非常に幅広いトピックであるため、基礎となる数学の詳細については説明しません。この数学の現れを利用する方が良いです。説明した手法を適用することにより、ポジションロックのスワップによって引き起こされる損失を減らすことができます。また、ブローカーのスワップテーブルのギャップを見つけて、正の利益係数(すべてのポジションの収益性の高いトータルスワップ)でロックを楽しむこともできます。これは、価格変動に依存しないリスクのない取引です。

ポジティブスワップは潜在的な利益をもたらすので、スワップ取引手法は本当に過小評価されていると思います。説明されている手法はスワップ取引手法の可能なバリエーションの1つにすぎません。私はこのタスクが好きで、次の記事では引き続きアイデアを開発し、コードを最新化し、新しい追加機能を作成します。また、利益予測と取引機能に関するいくつかのアイデアについても説明します。

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/9198

添付されたファイル |

ZIPをダウンロード

Prototype.zip (20.52 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。