
Swaps (Teil I): Locking und synthetische Positionen
Inhaltsverzeichnis
- Einführung
- Über Swaps
- Locking mit zwei Handelskonten
- Über Wechselkurse
- Locking unter Verwendung synthetischer Positionen
- Schreiben eines Hilfsprogramms zur Verwendung von Swap-Polygonen
- Schlussfolgerungen aus den ersten Tests
- Schlussfolgerung
Einführung
Ich habe lange über das Thema dieses Artikels nachgedacht, aber ich hatte keine Zeit, eine detaillierte Recherche durchzuführen. Das Thema Swaps ist im Web recht weit verbreitet, vor allem unter Trading-Profis, die jeden Pip zählen, was eigentlich der beste Ansatz für den Handel ist. Aus diesem Artikel erfahren Sie, wie Sie Swaps sinnvoll einsetzen können und werden sehen, dass die Swaps immer berücksichtigt werden müssen. Außerdem enthält der Artikel eine sehr komplexe, aber interessante Idee, wie man Swap-Handelsmethoden modernisieren kann. Solche Methoden können (wenn sie richtig vorbereitet sind) innerhalb eines Kontos oder als gewinnsteigerndes Werkzeug für das klassische Schließen mit zwei Konten verwendet werden.
Über Swaps
Ich werde nicht die Idee der Swaps und ihre Theorie erklären. Ich interessiere mich nur für die praktische Anwendung von Swaps. Die wichtigste Frage ist, ob es möglich ist, über Swaps Gewinn zu erzielen. Aus der Sicht eines Händlers ist ein Swap ein Gewinn oder ein Verlust. Darüber hinaus wird er von vielen Händlern einfach ignoriert, da sie sich an den Intraday-Handel halten. Andere versuchen, ihm keine Beachtung zu schenken, weil sie denken, dass er so unbedeutend ist, dass er den Handel kaum beeinflussen kann. Tatsächlich kann fast die Hälfte des Spreads im Swap versteckt sein. Dieser Spread wird nicht zum Zeitpunkt des Kaufs oder Verkaufs genommen, sondern wenn der Tag auf dem Server wechselt.
Der Swap wird relativ zum offenen Positionsvolumen berechnet. Dies geschieht zu den folgenden Zeitpunkten:
- Von Montag auf Dienstag
- Von Dienstag auf Mittwoch
- Von Mittwoch auf Donnerstag (fast alle Broker berechnen in dieser Nacht einen dreifachen Swap)
- Von Donnerstag auf Freitag
Normalerweise wird der Swap-Wert in der Spezifikation des Handelsinstruments in Punkten oder als Prozentsatz angegeben. Es kann auch andere Berechnungsmethoden geben, aber ich habe es geschafft, nur zwei von ihnen zu verstehen, was völlig ausreichend ist. Es gibt sehr wenig strukturierte Informationen über Swaps. Wenn Sie jedoch die Frage studieren, können Sie sogar einige effiziente Swap-basierte Strategien finden. Sie generieren minimale Gewinnprozente, aber sie haben einen großen Vorteil — der Gewinn ist absolut garantiert. Die Hauptschwierigkeit dieses Ansatzes ist die Tatsache, dass die populärsten Broker nur sehr wenige Instrumente mit einem positiven Swap haben, so dass es wirklich schwer ist, mit dieser Idee Geld zu verdienen. Auch der mögliche potentielle Gewinn ist extrem niedrig. Nichtsdestotrotz ist dies besser, als die Einlage komplett zu verlieren. Und wenn Sie ein anderes Handelssystem verwenden, werden Sie es höchstwahrscheinlich verlieren.
Die Quintessenz meiner Schlussfolgerungen bezüglich des Forex-Handels ist, dass nichts einen Gewinn garantieren kann, außer positiven Swaps. Natürlich gibt es einige Systeme, die in der Lage sind, einen Gewinn zu erwirtschaften. Aber wenn wir sie benutzen, stimmen wir zu, unser Geld an den Broker für jede Handelsoperation zu zahlen, und wir hoffen, dass der Preis in die richtige Richtung geht. Ein positiver Swap ist der umgekehrte Prozess. Ich sehe die folgenden Aussagen als die Kennzeichen des Handels in der positiven Swap-Richtung:
- Ein positiver Swap ist gleichbedeutend mit einer teilweisen Preisbewegung in Richtung unserer offenen Position (täglicher Gewinn)
- Nach einer gewissen Zeit kann ein Swap Verluste bei Spreads und Kommissionen ausgleichen; nach einer gewissen Zeit wird der Swap Geld hinzufügen
- Damit der Swap funktioniert, sollte die Position so lange wie möglich gehalten werden, dann wird der Gewinnfaktor dieser Positionen maximal sein
- Wenn es gründlich entwickelt wird, wird der Gewinn absolut vorhersehbar und garantiert sein
Der größte Nachteil dieses Ansatzes ist natürlich die Abhängigkeit von der Höhe der Einlage, aber kein anderes Konzept ist in der Lage, den Gewinn im Forex so sicher zu garantieren. Diese Abhängigkeit kann reduziert werden, indem man das Volumen der offenen Positionen oder das Risiko (was dasselbe ist) reduziert. Das Risiko ist das Verhältnis des Positionsvolumens zur Einlage: eine Erhöhung des Positionsvolumens erhöht unser Risiko, dass der Preis in die Verlustrichtung geht und die Einlage nicht ausreicht, um auf den Gewinn aus den Swaps zu warten, um die Verluste aus den Spreads und Provisionen zu kompensieren. Um den Einfluss aller möglichen negativen Effekte zu minimieren, wurde Locking, ein Sperrmechanismus, erfunden.
Locking mit zwei Handelskonten
Diese Swap-Handelsmethode ist die beliebteste unter den Händlern. Um diese Strategie zu implementieren, benötigen Sie zwei Konten mit unterschiedlichen Swaps für dieselben Währungspaare oder andere Assets. Die Eröffnung von zwei entgegengesetzten Positionen innerhalb desselben Kontos ist sinnlos — es ist gleichbedeutend mit dem einfachen Verlust der Einlage. Selbst wenn ein Symbol einen positiven Swap hat, wird dieser Swap negativ sein, wenn Sie in die entgegengesetzte Richtung handeln. Das folgende Diagramm spiegelt das Konzept dieser Methode wider:
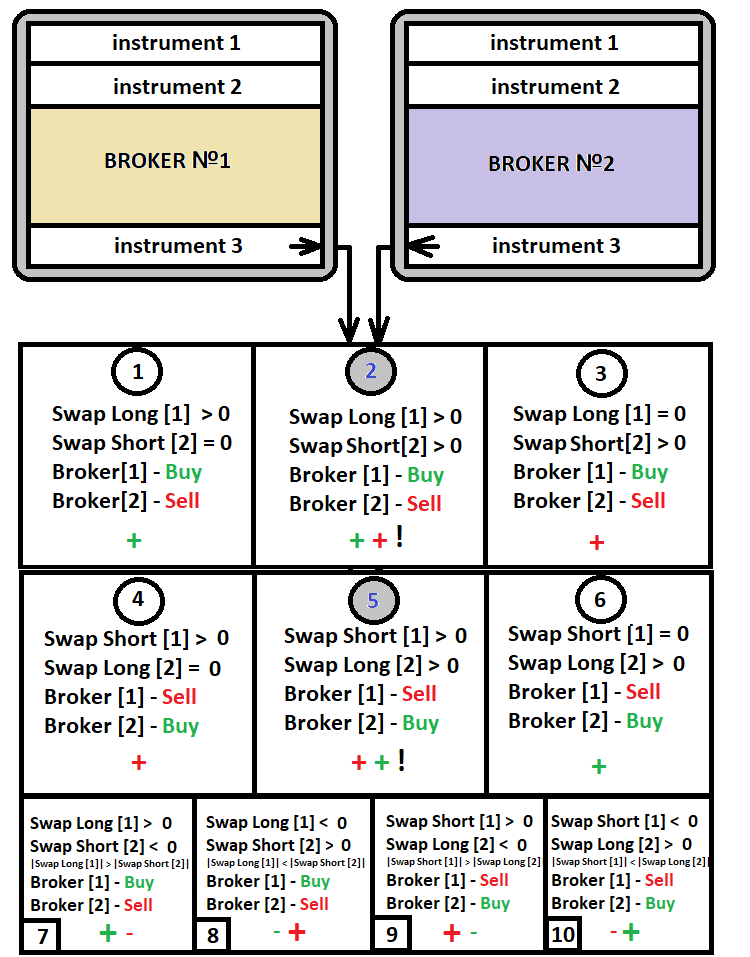
Wie Sie aus der Darstellung ersehen können, gibt es für ein speziell ausgewähltes Instrument, für das wir Swaps handeln wollen, nur 10 Handelsszenarien, von denen 6 aktiv genutzt werden. Die letzten vier Optionen können als letzter Ausweg gewählt werden, wenn es unmöglich ist, ein Währungspaar zu finden, das den Bedingungen "1-6" entspricht, da einer der Swaps hier negativ ist. Profitieren kann man von dem positiven Swap, der größer ist als der negative. Sie können alle oben genannten Fälle finden, wenn Sie verschiedene Broker und deren Swap-Tabellen analysieren. Aber die besten Optionen für diese Strategie sind "2" und "5". Diese Optionen haben positive Swaps an beiden Enden. Also wird der Gewinn von beiden Brokern erzielt. Außerdem müssen Sie nicht so oft Gelder zwischen den Konten verschieben.
Der Hauptnachteil dieser Strategie ist, dass Sie immer noch Geld zwischen den Konten verschieben müssen, denn wenn Sie gegensätzliche Positionen eröffnen, werden Sie Verlust bei einem Broker und Gewinn bei einem anderen Broker haben. Wenn Sie jedoch die Handelsvolumina im Verhältnis zum vorhandenen Depot richtig berechnen, werden Sie nicht so oft Geldmittel verschieben müssen. Aber es gibt einen unbestreitbaren Vorteil: In jedem Fall wird es einen Gewinn geben, wobei die genaue Größe dieses Gewinns vorhergesagt werden kann. Ich denke, viele Benutzer würden es vorziehen, diese Routine zu vermeiden und irgendwie diese Manipulationen innerhalb eines Kontos durchzuführen (was unmöglich ist). Aber es gibt eine Methode, wie man den Gewinn der klassischen Swap-Handelsmethode erhöhen kann, obwohl sie den Handel innerhalb eines Kontos nicht erlaubt. Lassen Sie uns die Hauptmerkmale dieser Methode besprechen.
Über Wechselkurse
Beginnen wir mit der Basis, auf der alle Logik aufgebaut ist. Mathematische Gleichungen können auf dieser Basis aufgebaut werden. Betrachten wir zum Beispiel EURUSD, USDJPY, EURJPY. Alle diese 3 Paare sind miteinander korreliert. Um die Beziehung zu verstehen, lassen Sie uns diese Symbole in einer etwas anderen Form darstellen:
- 1/P = EUR/USD
- 1/P = USD/JPY
- 1/P = EUR/JPY
- P ist der Kurs der gewählten Währung
Jedes Handelsinstrument hat eine Währung (oder ein gleichwertiges Asset), die wir erwerben, und eine andere Währung, die wir im Gegenzug abgeben. Wenn Sie zum Beispiel das erste Verhältnis (das EURUSD-Paar) nehmen, dann erwerben Sie beim Öffnen einer 1-Lot-Kaufposition 100.000 Einheiten der Basiswährung. Das sind die Regeln des Forex-Handels: ein Lot ist immer gleich 100.000 Einheiten der Basiswährung. Die Basiswährung dieses Paares ist EUR und somit kaufen wir EUR für USD. Der Währungskurs "P" bedeutet in diesem Fall, wie viele Einheiten von USD in 1 EUR enthalten sind. Das Gleiche gilt für alle anderen Symbole: die Basiswährung ist im Zähler enthalten, während der Nenner die "Hauptwährung" ist (wenn Sie mit dieser Namensgebung nicht einverstanden sind, vermerken Sie das bitte unten im Kommentarteil). Der Betrag der Hauptwährung wird einfach durch Multiplikation des Preises mit dem EUR-Wert berechnet:
- 1/P = EUR/USD ---> USD/P = EUR ---> USD = P*EUR
- EUR = Lots*100000
Beim Eröffnen einer Verkaufsposition tauschen die Währungen die Plätze. Die Basiswährung beginnt als Hauptwährung zu fungieren, und die Hauptwährung wird zur Basiswährung. Mit anderen Worten, wir kaufen USD für EUR, aber die Geldmenge beider Währungen wird auf die gleiche Weise berechnet — relativ zu EUR. Das ist richtig, denn sonst gäbe es ziemlich viel Verwirrung. Die Berechnungen sind für andere Währungen gleich. Lassen Sie uns also in der weiteren Berechnung das Zeichen "+" für die Basiswährung und das Zeichen "-" für die Hauptwährung verwenden. Als Ergebnis hat jeder Handel einen Satz von zwei entsprechenden Zahlen, die symbolisieren, was und wofür wir kaufen. Eine andere Interpretation davon ist, dass es immer eine Währung gibt, die als Produkt fungiert und eine andere Währung, die als Währung fungiert und die wir bezahlen, um das Produkt zu kaufen.
Wenn wir mehrere Positionen für mehrere Instrumente öffnen, dann gibt es mehrere Haupt- und Nebenwährungen, und so haben wir eine Art synthetische Position. Aus der Sicht der Verwendung von Swaps ist eine solche synthetische Position absolut nutzlos. Aber wir können eine solche synthetische Position erstellen, die sehr nützlich sein wird. Ich werde sie etwas später zeigen. Ich habe die Berechnung des Volumens, ausgedrückt durch zwei Währungen, bestimmt. Daraus können wir schließen, dass wir eine komplexe synthetische Position erstellen können, die einer einfacheren Position entspricht:
- EUR/JPY = EUR/USD * USD/JPY — Währungskurs bestehend aus zwei Derivaten
In Wirklichkeit gibt es eine unendliche Anzahl solcher Verhältnisse, die sich aus mehreren Währungen zusammensetzen, wie z.B.:
- EUR - Europäischer Euro
- USD - Amerikanischer Dollar
- JPY - Japanischer Yen
- GBP - Britisches Pfund
- CHF - Schweizer Franken
- CAD - Kanadischer Dollar
- NZD - Neuseeländischer Dollar
- AUD - Australischer Dollar
- CNY - Chinesischer Yuan
- SGD - Singapur-Dollar
- NOK - Norwegische Krone
- SEK - Schwedische Krone
Dies ist nicht die vollständige Liste der Währungen. Was wir wissen müssen, ist, dass ein beliebiges Handelsinstrument aus beliebigen Währungen aus dieser Liste zusammengesetzt werden kann. Einige dieser Handelsinstrumente werden von Brokern angeboten, während andere als eine Kombination von Positionen anderer Instrumente erhalten werden können. Ein typisches Beispiel ist das EURJPY-Paar. Dies ist nur das einfachste Beispiel für die Zusammenstellung von derivativen Devisenkursen, aber basierend auf diesen Ideen können wir schlussfolgern, dass jede Position als eine Reihe von Positionen für andere Instrumente dargestellt werden kann. Nach dem oben Gesagten stellt sich heraus, dass:
- Wert1 ist die Basis-Symbolwährung, ausgedrückt durch einen absoluten Wert
- Wert2 ist eine zusätzliche Symbolwährung, die durch einen absoluten Wert ausgedrückt wird
- A ist das Lotvolumen der Basiswährung der Position
- B ist das Lotvolumen der Hauptwährung der Position
- Kontrakt ist der Betrag der gekauften oder verkauften Währung in absolutem Wert (entspricht 1 Lot)
- A = 1/P = Wert1/Wert2 - das ist die Gleichung eines beliebigen Handelsinstruments (einschließlich derjenigen, die nicht im Marktbeobachtungsfenster angezeigt werden)
- Wert1 = Kontrakt*A
- Wert2 = Kontrakt*B
Wir werden diese Verhältnisse später zur Berechnung von Lots benötigen. Für den Moment merken Sie sie sich bitte. Diese Verhältnisse beschreiben das Verhältnis der Anzahl von Währungen, die gekauft oder verkauft werden. Auf dieser Basis kann eine ernsthaftere Codelogik aufgebaut werden.
Locking unter Verwendung synthetischer Positionen
In diesem Artikel ist eine synthetische Position eine Position, die aus mehreren anderen Positionen zusammengesetzt werden kann, wobei diese anderen Positionen notwendigerweise aus anderen Instrumenten zusammengesetzt sein müssen. Diese Position muss für ein beliebiges Instrument gleichwertig zu einer offenen Position sein. Klingt kompliziert? Eigentlich ist das alles ganz einfach. Eine solche Position kann benötigt werden, um:
- Sichern (Lock) der ursprünglichen Position für ein simuliertes Handelsinstrument
- Versuch das Äquivalent einer Position mit völlig anderen Swap-Sätzen zu erstellen
- Andere Zwecke
Hier ist das allgemeine Schema dieser Methode:
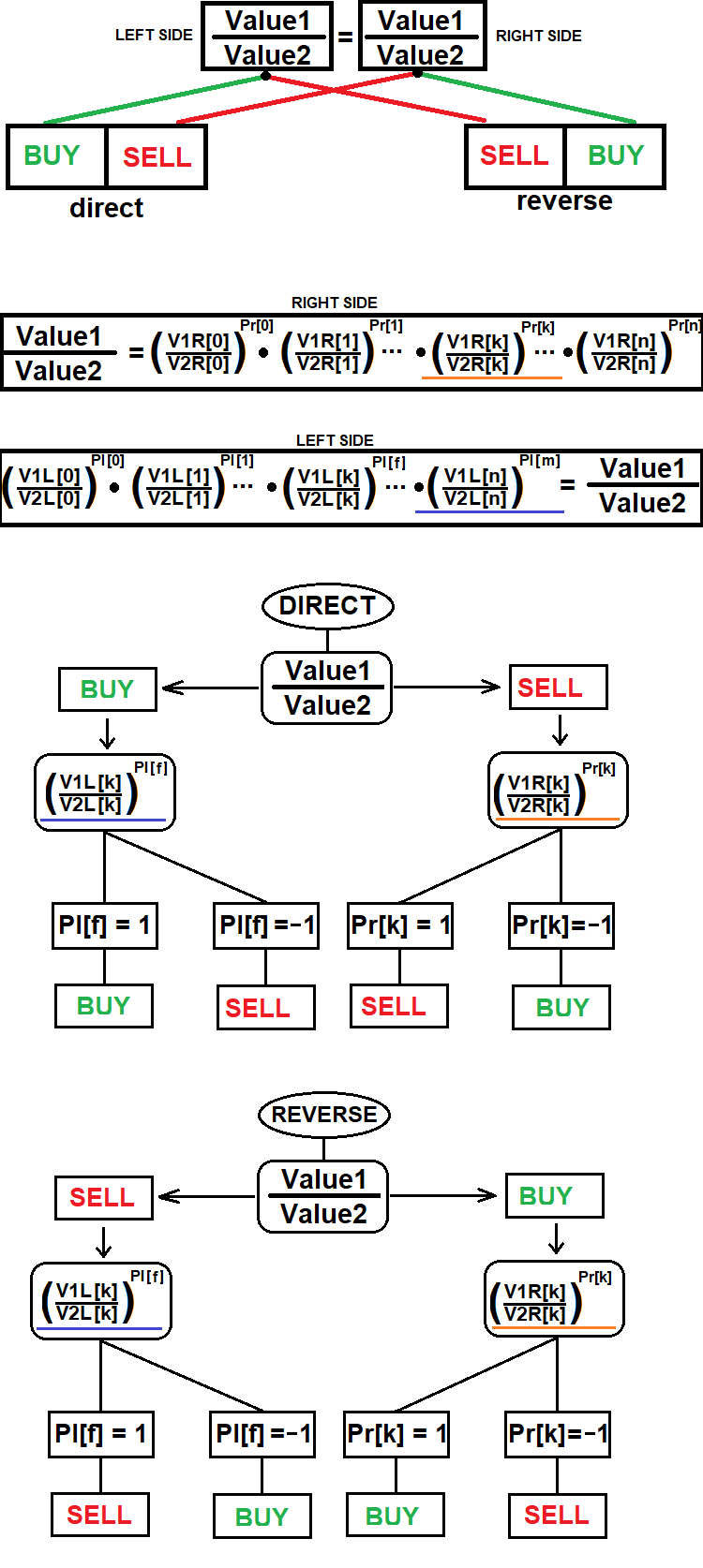
Auch dieses Schema deckt nicht die vollständigen Daten darüber ab, wie eine synthetische Position zu eröffnen ist. Dieses Schema zeigt nur, wie man die Handelsrichtung für eine bestimmte Komponente einer synthetischen Position bestimmt, die notwendigerweise durch eines der verfügbaren Instrumente des gewählten Brokers dargestellt werden muss.
Nun müssen wir bestimmen, wie wir die Volumina dieser Positionen berechnen. Logischerweise sollten die Volumina auf der Grundlage der Überlegung berechnet werden, dass die Position einer 1-Lot-Position für das resultierende Instrument entsprechen sollte, auf das die gewählte Variante der Gleichung reduziert wird. Für die Volumenberechnung werden folgende Werte benötigt:
- KontraktB - die Kontraktgröße des Paares, auf das die Gleichung reduziert wird (in den meisten Fällen ist sie gleich 100.000 Einheiten der Basiswährung)
- Kontrakt[1] - die Kontraktgröße des Paares, für das Sie das Lot bestimmen möchten
- A[1] - der Betrag der Basiswährung, ausgedrückt in Lots des vorherigen ausgeglichenen Paares (oder des ersten in der Kette)
- B[1] - der Betrag der Hauptwährung ausgedrückt in Lots des vorherigen ausgeglichenen Paares (oder des ersten in der Kette)
- A[2] - der Betrag der Basiswährung, ausgedrückt in Lots des aktuell ausgeglichenen Paares
- B[2] - der Betrag der Hauptwährung, ausgedrückt in Lots des aktuellen Paares, das ausgeglichen wird
- C[1] - Kontraktgröße des vorherigen ausgeglichenen Paares (oder des ersten Paares in der Kette)
- C[2] - Kontraktgröße des aktuell ausgeglichenen Paares
Bitte beachten Sie, dass es nicht immer möglich ist, "KontraktB" zu bestimmen, da das aus der Kombination resultierende Instrument möglicherweise nicht vom Broker bereitgestellt wird. In diesem Fall kann der Kontrakt willkürlich festgelegt werden, z.B. gleich der Grundkonstante "100000".
Zunächst wird das erste Paar in der Kette ermittelt, das die Basiswährung des resultierenden Instruments an der gewünschten Stelle enthält. Dann werden weitere Paare gesucht, die die zusätzlichen Währungen ausgleichen, die nicht im resultierenden Äquivalent enthalten sind. Der Ausgleich endet, wenn sich die Hauptwährung in der richtigen Position im aktuellen Paar befindet. Ich habe ein Diagramm erstellt, um zu zeigen, wie dies gemacht wird:
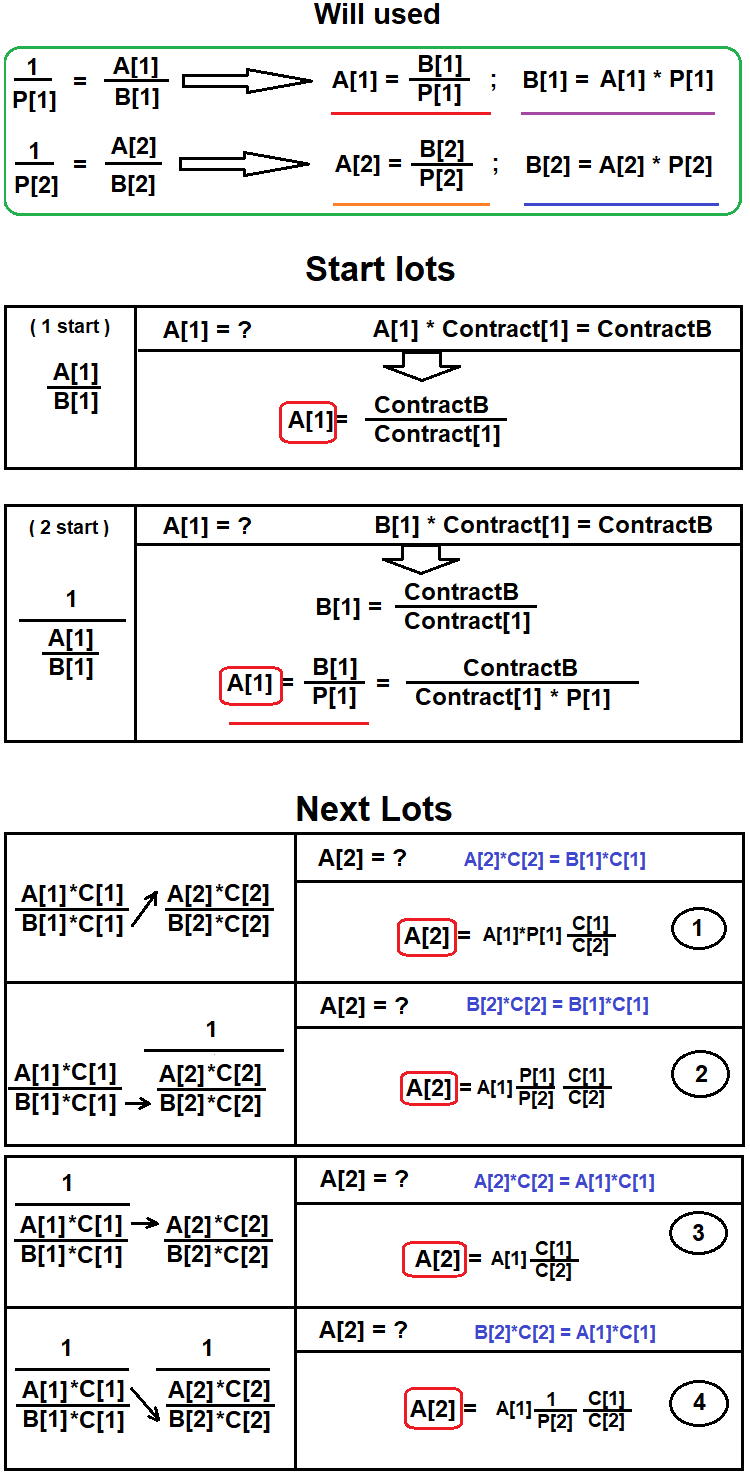
Nun wollen wir diese Techniken im Code implementieren und die Ergebnisse analysieren. Der erste Prototyp wird sehr einfach sein, da sein einziger Zweck darin besteht, die Korrektheit der Ideen zu bewerten. Ich hoffe, dass die obigen Diagramme Ihnen helfen werden, alle Details der Idee zu verstehen.
Schreiben eines Hilfsprogramm zum Untersuchen von Tauschpolygonen
Die Sortierung und Datenaufbereitung der Marktübersicht:
Um diese Technik zu verwenden, ist es notwendig, nur solche Paare auszuwählen, deren Namen genau 6 Zeichen lang sind und nur aus Großbuchstaben bestehen. Ich denke, alle Broker halten sich an diese Benennungsregel. Einige Broker fügen Präfixe oder Postfixe hinzu, die beim Schreiben von Algorithmen für die Arbeit mit String-Daten ebenfalls berücksichtigt werden sollten. Um die Symbolinformationen in einem geeigneten Format zu speichern, habe ich zwei Strukturen angelegt (die zweite wird später verwendet):
struct Pair// required symbol information { string Name;// currency pair double SwapBuy;// buy swap double SwapSell;// sell swap double TickValue;// profit from 1 movement tick of a 1-lot position double TickSize;// tick size in the price double PointX;// point size in the price double ContractSize;// contract size in the base deposit currency double Margin;// margin for opening 1 lot }; struct PairAdvanced : Pair// extended container { string Side;// in numerator or denominator double LotK;// lot coefficient double Lot;// lot };
Einige Felder werden beim Sortieren von Paaren nicht verwendet. Um keine unnötigen Container zu produzieren, habe ich ihn etwas erweitert, damit die Struktur auch für andere Zwecke verwendet werden kann. Ich hatte einen Prototyp eines ähnlichen Algorithmus, aber mit sehr eingeschränkten Möglichkeiten: Er konnte nur die Paare berücksichtigen, die sich im Hauptterminalfenster befanden. Jetzt ist alles einfacher. Und was noch wichtiger ist, alle Operationen sind im Algorithmus automatisiert. Die folgende Funktion wird benötigt, um die Größe des Arrays mit Instrumenten festzulegen:
Pair Pairs[];// data of currency pairs void SetSizePairsArray()// set size of the array of pairs { ArrayResize(Pairs,MaxSymbols); ArrayResize(BasicPairsLeft,MaxPairs*2); // since each pair has 2 currencies, there can be a maximum of 2 times more base currencies ArrayResize(BasicPairsRight,MaxPairs*2);// since each pair has 2 currencies, there can be a maximum of 2 times more base currencies }
In der ersten Zeile wird die maximale Anzahl der Paare aus dem Fenster "Marktübersicht" festgelegt, die wir verwenden können. Die anderen beiden Zeilen legen die Größe der Arrays fest, die verwendet werden sollen. Die verbleibenden 2 Arrays spielen eine Hilfsrolle — sie ermöglichen die Aufteilung eines Währungspaares in 2 Teile (2 zusammengesetzte Währungen). Die gelb hervorgehobenen Variablen sind die Eingabeparameter des EA.
- MaxSymbols - maximale Speichergröße der Paare (ich habe die manuelle Angabe implementiert)
- MaxPairs - die maximale Anzahl von Paaren in beiden Teilen der Formel, die wir generieren (Formeln, die länger als diese Zahl sind, werden vom Expert Advisor nicht durchsucht)
Um zu prüfen, ob ein Handelsinstrument die Kriterien erfüllt (Zeichen von zwei verschiedenen Währungen, die potenziell in anderen Instrumenten vorhanden sein können), habe ich die folgende Prädikatsfunktion erstellt:
bool IsValid(string s)// checking the instrument validity (its name must consist of upper-case letters) { string Mask="abcdefghijklmnopqrstuvwxyz1234567890";// mask of unsupported characters (lowercase letters and numbers) for ( int i=0; i<StringLen(s); i++ )// reset symbols { for ( int j=0; j<StringLen(Mask); j++ ) { if ( s[i] == Mask[j] ) return false; } } return true; }
Diese Funktion ist nicht die einzige Bedingung für zukünftige Prüfungen von Geräten. Aber diese Bedingung kann nicht innerhalb eines logischen Ausdrucks geschrieben werden, daher ist es einfacher, sie als Prädikat zu implementieren. Gehen wir nun zur Hauptfunktion über, die das Array mit den notwendigen Daten füllt:
void FillPairsArray()// fill the array with required information about the instruments { int iterator=0; double correction; int TempSwapMode; for ( int i=0; i<ArraySize(Pairs); i++ )// reset symbols { Pairs[iterator].Name=""; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { TempSwapMode=int(SymbolInfoInteger(Pairs[iterator].Name,SYMBOL_SWAP_MODE)); if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) && SymbolInfoInteger(SymbolName(i,false),SYMBOL_TRADE_MODE) == SYMBOL_TRADE_MODE_FULL && ( ( TempSwapMode == 1 ) || ( ( TempSwapMode == 5 || TempSwapMode == 6 ) && CorrectedValue(Pairs[iterator].Name,correction) )) ) { if ( iterator >= ArraySize(Pairs) ) break; Pairs[iterator].Name=SymbolName(i,false); Pairs[iterator].TickSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_SIZE); Pairs[iterator].PointX=SymbolInfoDouble(Pairs[iterator].Name, SYMBOL_POINT); Pairs[iterator].ContractSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_CONTRACT_SIZE); switch(TempSwapMode) { case 1:// in points Pairs[iterator].SwapBuy=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); Pairs[iterator].SwapSell=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); break; case 5:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; case 6:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; } Pairs[iterator].Margin=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_MARGIN_INITIAL); Pairs[iterator].TickValue=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_VALUE); iterator++; } } }
Diese Funktion bietet eine einfache Iteration aller Symbole und eine Filterung durch eine komplexe zusammengesetzte Bedingung, die sowohl die Einhaltung der Anforderung an die Länge des Zeichenkettennamens als auch die Möglichkeit, dieses Symbol zu handeln, überprüft, sowie weitere Parameter, die sich auf diejenigen Symbole beziehen, für die die Swap-Berechnungsmethode von der am häufigsten verwendeten auf "in Punkten" abweicht. Eine der Swap-Berechnungsmethoden wird im "switch"-Block ausgewählt. Derzeit sind zwei Methoden implementiert: in Punkten und in Prozent. Die richtige Sortierung ist vor allem wichtig, um unnötige Berechnungen zu vermeiden. Beachten Sie bitte auch die rot markierte Funktion. Wenn die Hauptwährung (nicht die Basiswährung) durch eine Währung repräsentiert wird, die nicht mit der Einzahlungswährung übereinstimmt, sollte ein bestimmter Anpassungsfaktor hinzugefügt werden, um den Swap in die Einzahlungswährung umzuwandeln. Diese Funktion errechnet die entsprechenden Werte. Das ist deren Code:
bool CorrectedValue(string Pair0,double &rez)// adjustment factor to convert to deposit currency for the percentage swap calculation method { string OurValue=AccountInfoString(ACCOUNT_CURRENCY);// deposit currency string Half2Source=StringSubstr(Pair0,PrefixE+3,3);// lower currency of the pair to be adjusted if ( Half2Source == OurValue ) { rez=1.0; return true; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) )//find the currency rate to convert to the account currency { string Half1=StringSubstr(SymbolName(i,false),PrefixE,3); string Half2=StringSubstr(SymbolName(i,false),PrefixE+3,3); if ( Half2 == OurValue && Half1 == Half2Source ) { rez=SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } if ( Half1 == OurValue && Half2 == Half2Source ) { rez=1.0/SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } } } return false; }
Diese Funktion dient als Prädikat und gibt den Wert des Anpassungsfaktors an die Variable zurück, die von außen per Referenz übergeben wurde. Der Anpassungsfaktor wird auf der Grundlage des Kurses der gewünschten Währung berechnet, zu der auch unsere Einzahlungswährung gehört.
Zufällig generierte Formeln
Angenommen, das Array wurde mit den erforderlichen Daten gefüllt. Nun müssen wir irgendwie über diese Symbole iterieren und versuchen, "on-the-fly" alle möglichen Kombinationen von Formeln zu erzeugen, die sich aus diesen Paaren bilden lassen. Zunächst muss entschieden werden, in welcher Form die Formel gespeichert werden soll. Die Struktur, in der alle Elemente dieser Formel gespeichert werden, sollte sehr einfach und übersichtlich für die Benutzer sein, für den Fall, dass die Notwendigkeit besteht, Protokolle einzusehen (wobei es definitiv eine solche Notwendigkeit geben wird, sonst wird es unmöglich sein, Fehler zu identifizieren).
Unsere Formel ist ein Satz von Faktoren sowohl links als auch rechts des "="-Zeichens. Der Faktor kann der Währungskurs in der Potenz von 1 oder -1 sein (was einem umgekehrten Bruch entspricht, oder eine Einheit bezogen auf den aktuellen Instrumentenkurs). Ich habe mich entschieden, die folgende Struktur zu verwenden:
struct EquationBasic // structure containing the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula };
Alle Daten werden als Text gespeichert. Um die Formel zu studieren, werden die Zeichenketten geparst, um alle notwendigen Informationen zu extrahieren, die wir benötigen. Außerdem können sie bei Bedarf ausgedruckt werden. Die generierten Formeln werden in der folgenden Form ausgedruckt:
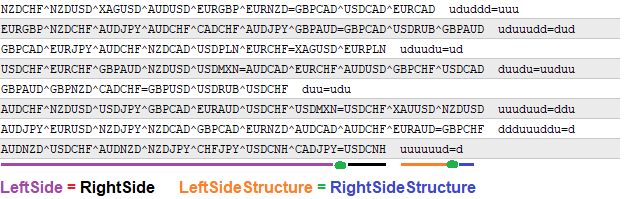
Für mich persönlich ist ein solcher Datensatz absolut übersichtlich und lesbar. Das Zeichen "^" wird als Trennzeichen zwischen Paaren verwendet. In der Formelstruktur werden keine Trennzeichen benötigt, da sie aus den Einzelzeichen "u" und "d" besteht, die den Grad des Multiplikators angeben:
- "u" ist der Währungskurs
- "d" ist 1/Währungskurs
Wie Sie sehen, haben die resultierenden Formeln eine gleitende Länge und eine gleitende Größe der beiden Seiten der Gleichung, aber diese Größe hat ihre Grenzen. Dieser Ansatz bietet die maximale Variabilität der generierten Formeln. Dies wiederum sorgt für die höchstmögliche Qualität der gefundenen Varianten innerhalb der Handelsbedingungen des gewählten Brokers. Die Broker stellen völlig unterschiedliche Bedingungen zur Verfügung. Um die erfolgreiche Generierung dieser Formeln zu gewährleisten, benötigen wir zusätzliche Zufallsfunktionen, die Zahlen im gewünschten Bereich generieren können. Zu diesem Zweck wollen wir die entsprechende Funktionalität mit Hilfe der Fähigkeiten der integrierten Zufallsfunktion MathRand erstellen:
int GenerateRandomQuantityLeftSide()// generate a random number of pairs on the left side of the formula { int RandomQuantityLeftSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-1))); if ( RandomQuantityLeftSide >= MaxPairs ) return MaxPairs-1; return RandomQuantityLeftSide; } int GenerateRandomQuantityRightSide(int LeftLenght)// generate a random number of pairs on the right side of the formula (taking into account the number of pairs on the left side) { int RandomQuantityRightSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-LeftLenght))); if ( RandomQuantityRightSide < 2 && LeftLenght == 1 ) return 2;// there must be at least 2 pairs in one of the sides, otherwise it will be equivalent to opening two opposite positions if ( RandomQuantityRightSide > (MaxPairs-LeftLenght) ) return (MaxPairs-LeftLenght); return RandomQuantityRightSide; } int GenerateRandomIndex()// generate a random index of a symbol from the MarketWatch window { int RandomIndex=0; while(true) { RandomIndex=int(MathFloor((double(MathRand())/32767.0) * double(MaxSymbols)) ); if ( RandomIndex >= MaxSymbols ) RandomIndex=MaxSymbols-1; if ( StringLen(Pairs[RandomIndex].Name) > 0 ) return RandomIndex; } return RandomIndex; }
Alle drei Funktionen werden in einem bestimmten Stadium benötigt. Jetzt können wir die Funktion schreiben, die diese Formeln erzeugt. Der Code wird immer komplexer werden, aber ich werde keinen objektorientierten Ansatz verwenden, da die Aufgabe nicht standardisiert ist. Ich habe mich für einen prozeduralen Ansatz entschieden. Die resultierenden Prozeduren sind ziemlich groß und umständlich, aber es gibt keine zusätzliche Funktionalität, und jede Funktion implementiert eine bestimmte Aufgabe, ohne irgendwelche Zwischenfunktionen zu verwenden, um Code-Duplizierung zu vermeiden. Ansonsten wäre der Code aufgrund der Aufgabenspezifika noch schwerer zu verstehen. Die Funktion sieht dann wie folgt aus:
EquationBasic GenerateBasicEquation()// generate both parts of the random equation { int RandomQuantityLeft=GenerateRandomQuantityLeftSide(); int RandomQuantityRight=GenerateRandomQuantityRightSide(RandomQuantityLeft); string TempLeft=""; string TempRight=""; string TempLeftStructure=""; string TempRightStructure=""; for ( int i=0; i<RandomQuantityLeft; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == 0 && RandomQuantityLeft > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i != 0 && (RandomQuantityLeft-i) > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft-1 ) TempLeft+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempLeftStructure+="u"; else TempLeftStructure+="d"; } for ( int i=RandomQuantityLeft; i<RandomQuantityLeft+RandomQuantityRight; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == RandomQuantityLeft && RandomQuantityRight > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i != RandomQuantityLeft && (RandomQuantityLeft+RandomQuantityRight-i) > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft+RandomQuantityRight-1 ) TempRight+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempRightStructure+="u"; else TempRightStructure+="d"; } EquationBasic result; result.LeftSide=TempLeft; result.LeftSideStructure=TempLeftStructure; result.RightSide=TempRight; result.RightSideStructure=TempRightStructure; return result; }
Wie Sie sehen können, werden hier alle drei zuvor betrachteten Funktionen verwendet, um eine Zufallsformel zu erzeugen. Diese Funktionen werden nirgendwo sonst im Code verwendet. Sobald die Formel fertig ist, können wir zu einer schrittweisen Analyse dieser Formel übergehen. Alle fehlerhaften Formeln werden durch den nächsten, äußerst wichtigen, komplexen Filter verworfen. Zunächst wird auf Gleichheit geprüft. Wenn die Teile nicht gleich sind, dann ist diese Formel falsch. Alle konformen Formeln gehen zum nächsten Analyseschritt über.
Formelabgleich
Dieser Schritt umfasst mehrere Analysekriterien auf einmal:
- Zählen aller zusätzlichen Faktoren im Zähler und Nenner und Entfernen dieser Faktoren
- Prüfen der Verfügbarkeit von 1 Währung im Zähler und 1 Währung im Nenner
- Prüfen der Übereinstimmung der resultierenden Brüche auf der linken und rechten Seite
- Wenn die rechte Seite der Kehrwert der linken Seite ist, kehren wir einfach die rechte Struktur der Formel um (das ist ähnlich wie das Erhöhen auf die Potenz "-1")
- Wenn alle Schritte erfolgreich abgeschlossen sind, wird das Ergebnis in eine neue Variable geschrieben.
So sehen diese Schritte im Code aus:
BasicValue BasicPairsLeft[];// array of base pairs to the left BasicValue BasicPairsRight[];// array of base pairs to the right bool bBalanced(EquationBasic &CheckedPair,EquationCorrected &r)// if the current formula is balanced (if yes, return the corrected version to the "r" variable) { bool bEnd=false; string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } //// Calculate balance values for the left side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(CheckedPair.LeftSide,i,1); if ( Divider == "^" || i == StringLen(CheckedPair.LeftSide) - 1 ) { SubPair=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of left-side balance calculation //// Calculate balance values for the right side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(CheckedPair.RightSide,i,1); if ( Divider == "^"|| i == StringLen(CheckedPair.RightSide) - 1 ) { SubPair=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.RightSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of right-side balance calculation /// calculate the number of lower and upper currencies based on the received data from the previous block int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpLeft; string LastDownLeft; string LastUpRight; string LastDownRight; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity > 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[i].Quantity; if ( BasicPairsLeft[i].Quantity < 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[i].Quantity; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity > 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightUpTotal+=BasicPairsRight[i].Quantity; if ( BasicPairsRight[i].Quantity < 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightDownTotal-=BasicPairsRight[i].Quantity; } /// /// check if both sides are equal if ( LeftUpTotal == 1 && LeftDownTotal == 1 && RightUpTotal == 1 && RightDownTotal == 1 )// there must be one pair in the upper and in the lower part of both sides of the equality, otherwise the formula is invalid { for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity == 1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastUpLeft=BasicPairsLeft[i].Value; if ( BasicPairsLeft[i].Quantity == -1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastDownLeft=BasicPairsLeft[i].Value; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity == 1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastUpRight=BasicPairsRight[i].Value; if ( BasicPairsRight[i].Quantity == -1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastDownRight=BasicPairsRight[i].Value; } } else return false; if ( (LastUpLeft == LastUpRight && LastDownLeft == LastDownRight) || (LastUpLeft == LastDownRight && LastDownLeft == LastUpRight) ) { if ( LastUpLeft == LastDownRight && LastDownLeft == LastUpRight )// If the formula is cross-equivalent, then invert the structure of the right part of the equation (it is the same as raising to the power of -1) { string NewStructure;// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; } } else return false;// if the resulting fractions on both sides are not equivalent, then the formula is invalid if ( LastUpLeft == LastDownLeft ) return false;// if result in one, then the formula is invalid /// Now it is necessary to write all the above into a corrected and more convenient structure string TempResult=CorrectedResultInstrument(LastUpLeft+LastDownLeft,r.IsResultInstrument); if ( r.IsResultInstrument && LastUpLeft+LastDownLeft != TempResult ) { string NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.LeftSideStructure); i++ ) { if ( CheckedPair.LeftSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.LeftSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.LeftSideStructure=NewStructure; r.ResultInstrument=LastDownLeft+LastUpLeft; r.UpPair=LastDownLeft; r.DownPair=LastUpLeft; } else { r.ResultInstrument=LastUpLeft+LastDownLeft; r.UpPair=LastUpLeft; r.DownPair=LastDownLeft; } r.LeftSide=CheckedPair.LeftSide; r.RightSide=CheckedPair.RightSide; r.LeftSideStructure=CheckedPair.LeftSideStructure; r.RightSideStructure=CheckedPair.RightSideStructure; /// /// if code has reached this point, it is considered that we have found the formula meeting the criteria, and the next step is normalization return true; }
Die grün unterlegte Funktion wird benötigt, um festzustellen, ob die Liste der Symbole dasjenige enthält, auf das die Formel reduziert wurde. Es kann sich herausstellen, dass die Formel z. B. nicht auf "USDJPY", sondern auf "JPYUSD" reduziert wurde. Ein solches Symbol gibt es offensichtlich nicht, obwohl es erstellt werden könnte. Unsere Aufgabe ist es aber, die Formel so zu ändern, dass sie ein korrektes Handelsinstrument ergibt. In diesem Fall sollten beide Teile der Formel auf die Potenz von -1 angehoben werden, was einer Umkehrung der Struktur der Formel gleichkommt (ändern Sie "d" in "u" und umgekehrt). Wenn es kein solches Symbol im Market Watch-Fenster gibt, dann lassen Sie es so, wie es ist:
string CorrectedResultInstrument(string instrument, bool &bResult)// if any equivalent symbol corresponds to the generated formula, return this symbol (or leave as is) { string Half1=""; string Half2=""; string Half1input=StringSubstr(instrument,0,3);//input upper currency string Half2input=StringSubstr(instrument,3,3);//input lower currency bResult=false; for ( int j=0; j<ArraySize(Pairs); j++ ) { Half1=StringSubstr(Pairs[j].Name,PrefixE,3); Half2=StringSubstr(Pairs[j].Name,PrefixE+3,3); if ( (Half1==Half1input && Half2==Half2input) || (Half1==Half2input && Half2==Half1input) )// direct match or crossed match { bResult=true; return Pairs[j].Name; } } return instrument; }
Ich habe die folgende Struktur vorbereitet, um die Formeln zu speichern, die den Filter durchlaufen haben. Die Struktur hat einige Felder aus der vorherigen und einige neue Felder:
struct EquationCorrected // corrected structure of the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula string ResultInstrument;// the resulting instrument to which both parts of the formula come after transformation bool IsResultInstrument;// has the suitable equivalent symbol been found string UpPair;// the upper currency of the resulting instrument string DownPair;// the lower currency of the resulting instrument };
Normalisierung der Formeln
Dieser Vorgang ist der nächste Schritt beim Filtern der Ergebnisse. Er besteht aus den folgenden sequentiellen Operationen, die nacheinander folgen:
- Basierend auf dem resultierenden Symbol, das aus beiden Seiten der Gleichung erhalten wird, wählen Sie ein Startpaar aus der Liste für beide Seiten der Gleichheit.
- Beide Paare müssen, entsprechend ihrer Potenz in der Gleichung, die Basiswährung im Nenner des Bruches liefern
- Wenn ein solches Paar gefunden wird, und die untere Währung des Bruches nicht die Hauptwährung des resultierenden Instruments enthält, gehen wir weiter.
- Wir gehen auch weiter, sodass die obere Währung des nächsten Paares die untere Währung des vorherigen Paares ausgleicht.
- Wir wiederholen diese Schritte, bis das gewünschte resultierende Paar gefunden ist.
- Sobald das resultierende Paar gefunden ist, werden alle nicht verwendeten Komponenten der Formel verworfen (da ihr Produkt eins ist)
- Parallel zu diesem Prozess werden "Lot-Faktoren" sequentiell von Paar zu Paar berechnet (sie zeigen an, mit welchem Lot wir die Positionen für bestimmte Paare eröffnen müssen, um unser resultierendes Instrument zu gewährleisten).
- Das Ergebnis wird einer neuen Variable zugewiesen, die im nächsten Analyseschritt verwendet wird.
Der Funktionscode lautet wie folgt:
bool bNormalized(EquationCorrected &d,EquationNormalized &v)// formula normalization attempt (the normalized formula is returned in "v" ) { double PreviousContract;// previous contract bool bWasPairs;// if any pairs have been found double BaseContract;// contract of the pair to which the equation is reduced double PreviousLotK=0.0;// previous LotK double LotK;// current LotK string PreviousSubSide;// in numerator or denominator (previous factor) string PreviousPair;// previous pair string PreviousHalf1;// upper currency of the previous pair string PreviousHalf2;// lower currency of the previous pair string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity int tryiterator=0;// the number of balancing attempts int quantityleft=0;// the number of pairs on the left after normalization int quantityright=0;//the number of pairs on the right after normalization bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } if ( d.IsResultInstrument ) BaseContract=SymbolInfoDouble(d.ResultInstrument, SYMBOL_TRADE_CONTRACT_SIZE);// define the contract of the equivalent pair based on the instrument else BaseContract=100000.0; //// Calculate the number of pairs for the left side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.LeftSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } /// end of quantity calculation for the left part ArrayResize(v.PairLeft,tryiterator); /// calculate the lot coefficients for the left side bool bBalanced=false;// is the formula balanced bool bUsed[]; ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); int balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false;// have there been pairs for ( int k=0; k<tryiterator; k++ )// try to normalize the left side { if( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" || i == StringLen(d.LeftSide) - 1 ) { SubPair=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 1 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 2 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 3 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 4 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } v.PairLeft[balancediterator].Name=SubPair; v.PairLeft[balancediterator].Side=SubSide; v.PairLeft[balancediterator].ContractSize=SymbolInfoDouble(v.PairLeft[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityleft++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part string LastUpLeft; string LastDownLeft; for ( int z=0; z<ArraySize(BasicPairsLeft); z++ ) { if ( BasicPairsLeft[z].Quantity > 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[z].Quantity; if ( BasicPairsLeft[z].Quantity < 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[z].Quantity; } if ( bWasPairs && LeftUpTotal == 0 && LeftDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } /// end of coefficient calculation for the left part if ( !bBalanced ) return false;// if the left side is not balanced, then there is no point in balancing the right side //// Calculate the number of pairs for the right side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.RightSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } ArrayResize(v.PairRight,tryiterator); /// end of calculation of the number of pairs for the right side bBalanced=false;// is the formula balanced ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false; for ( int k=0; k<tryiterator; k++ )// try to normalize the right side { if ( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" || i == StringLen(d.RightSide) - 1 ) { SubPair=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.RightSideStructure,quantityiterator,1); Half1=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.RightSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (1) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (2) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (3) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (4) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } v.PairRight[balancediterator].Name=SubPair; v.PairRight[balancediterator].Side=SubSide; v.PairRight[balancediterator].ContractSize=SymbolInfoDouble(v.PairRight[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityright++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpRight; string LastDownRight; for ( int z=0; z<ArraySize(BasicPairsRight); z++ ) { if ( BasicPairsRight[z].Quantity > 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightUpTotal+=BasicPairsRight[z].Quantity; if ( BasicPairsRight[z].Quantity < 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightDownTotal-=BasicPairsRight[z].Quantity; } if ( bWasPairs && RightUpTotal == 0 && RightDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } if ( quantityleft == 1 && quantityright == 1 ) return false;// if the equation has been normalized to only 2 pairs, it is not valid (at least 3 pairs are required) return bBalanced; }
Dies ist ein sehr gesundes und komplexes Verfahren, aber es scheint mir, dass es in solchen Fällen besser ist, keine Zwischenzustände zu erzeugen, da dies zu erheblicher Verdopplung des Codes führen würde. Außerdem sind alle Stufen sehr kompakt und sie sind logisch in Blöcke unterteilt. Der Satz dieser Funktionen liefert uns absolut identische Ergebnisse, die mit den Ergebnissen vergleichbar sind, die wir erhalten könnten, wenn wir alle Konvertierungen handschriftlich durchführen würden. Hier werden alle diese mathematischen Manipulationen durch eine Reihe von komplexen, aber notwendigen Methoden durchgeführt.
Wir müssen eine spezielle Analyse durchführen, um zu verstehen, wie profitabel die gefundene Formel ist. Vergessen Sie nicht, dass es für jedes Paar möglich ist, eine Position sowohl nach oben als auch nach unten zu eröffnen. Dementsprechend kann es für jede Formel zwei Zwischenvarianten der Schaltungen geben - direkt und umgekehrt. Diejenige mit der höheren Rentabilität wird als Ergebnis angenommen.
Um die Rentabilität zu bewerten, habe ich eine dem Gewinnfaktor ähnliche Metrik geschaffen, die aus den Gewinnen und Verlusten besteht, die aus den Swaps resultieren. Wenn der aufgelaufene positive Swap der bestehenden Schaltung größer ist als der negative Modulus, dann wird eine solche Schaltung als profitabel angesehen. In anderen Fällen sind solche Schaltungen unrentabel — mit anderen Worten, der Swap-Faktor unserer Kontur wird nur dann positiv sein, wenn er größer als eins ist.
Das zurückgegebene Ergebnis wird in einen ganz anderen Container geschrieben, der als autarkes Befehlspaket für den Handel und für die Weiterentwicklung der Handelslogik erstellt wurde. Er enthält alles, was man braucht, um den gesamten Kreislauf schnell und einfach zu öffnen:
struct EquationNormalized // the final structure with the formula in normalized form { Pair PairLeft[];// currency pairs on the left side Pair PairRight[];// currency pairs on the right side double SwapPlusRelative;// relative equivalent of the positive swap double SwapMinusRelative;// relative equivalent of the negative swap double SwapFactor;// resulting swap factor };
Ich habe auch zwei Methoden hinzugefügt, die die komfortable Anzeige von Informationen über den Inhalt ermöglichen, aber sie sind für diesen Artikel nicht relevant und daher werde ich sie hier nicht bereitstellen. Sie können sie im angehängten Quellcode einsehen. Nun sind die Informationen über jede Komponente der Gleichung separat als Elemente von Arrays enthalten. Dies ermöglicht später ein einfacheres Arbeiten mit den Daten, ohne sie ständig aus den Zeichenketten extrahieren zu müssen. Vielleicht hätte man diese Lösung auch von Anfang an verwenden können, aber das hätte die Lesbarkeit beeinträchtigt.
Berechnung des Vertauschungsfaktors und endgültige Anpassung der Gleichungsstruktur
Dies ist der letzte Schritt, in dem die wichtigste Variable dieses Systems berechnet wird — die Varianten werden nach diesem Wert verglichen. Diejenige mit dem höchsten Wert ist die beste.
void CalculateBestVariation(EquationNormalized &ii)// calculation of the best swap factor of the formula and final structure adjustment if needed { double SwapMinus=0.0;// total negative swap double SwapPlus=0.0;// total positive swap double SwapMinusReverse=0.0;// total negative swap double SwapPlusReverse=0.0;// total positive swap double SwapFactor=0.0;// swap factor of the direct pass double SwapFactorReverse=0.0;// swap factor of the reverse pass for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// define the missing parameters for calculating the left side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairLeft[i].Name ) { ii.PairLeft[i].Margin=Pairs[j].Margin; ii.PairLeft[i].TickValue=Pairs[j].TickValue; ii.PairLeft[i].SwapBuy=Pairs[j].SwapBuy; ii.PairLeft[i].SwapSell=Pairs[j].SwapSell; break; } } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// define the missing parameters for calculating the right side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairRight[i].Name ) { ii.PairRight[i].Margin=Pairs[j].Margin; ii.PairRight[i].TickValue=Pairs[j].TickValue; ii.PairRight[i].SwapBuy=Pairs[j].SwapBuy; ii.PairRight[i].SwapSell=Pairs[j].SwapSell; break; } } } double TempSwap; // calculate all components taking into account a change in the structure for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// for left parts { if ( ii.PairLeft[i].Side == "u" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairLeft[i].Side == "d" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// for right parts { if ( ii.PairRight[i].Side == "d" ) {// for direct trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairRight[i].Side == "u" ) {// for direct trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } // calculate the swap factor for the direct pass if ( SwapMinus > 0.0 && SwapPlus > 0.0 ) SwapFactor=SwapPlus/SwapMinus; if ( SwapMinus == 0.0 && SwapPlus == 0.0 ) SwapFactor=1.0; if ( SwapMinus == 0.0 && SwapPlus > 0.0 ) SwapFactor=1000001.0; if ( SwapMinus > 0.0 && SwapPlus == 0.0 ) SwapFactor=0.0; // calculate the swap factor for the reverse pass if ( SwapMinusReverse > 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=SwapPlusReverse/SwapMinusReverse; if ( SwapMinusReverse == 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=1.0; if ( SwapMinusReverse == 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=1000001.0; if ( SwapMinusReverse > 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=0.0; // select the best approach and calculate the missing values in the structure if ( SwapFactor > SwapFactorReverse ) { ii.SwapPlusRelative=SwapPlus; ii.SwapMinusRelative=SwapMinus; ii.SwapFactor=SwapFactor; } else { ii.SwapPlusRelative=SwapPlusReverse; ii.SwapMinusRelative=SwapMinusReverse; ii.SwapFactor=SwapFactorReverse; bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// if it is a reverse pass, then reverse the right structure of the formula { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } bSigned=false; for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// if it is a reverse pass, then reverse the left structure of the formula { bSigned=false; if ( !bSigned && ii.PairLeft[i].Side == "u" ) { ii.PairLeft[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairLeft[i].Side == "d" ) { ii.PairLeft[i].Side="u"; bSigned=true; } } } bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// reverse the right side anyway { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } }
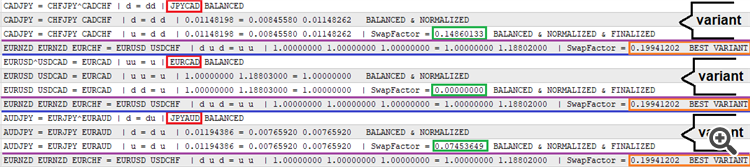
Um die sequentielle Ausgabe des Ergebnisses zu ermöglichen, habe ich das Protokoll implementiert, das nur geschrieben wird, wenn die erfolgreich gefilterte Formelvariante gefunden wird. Das Protokoll ergibt sich daher wie folgt:
Die rote Farbe wird für das resultierende Symbol verwendet, auf das beide Seiten der Gleichung reduziert werden. Die nächste Zeile zeigt die normierte Variante mit den Loskoeffizienten. Die dritte Zeile zeigt die Variante mit dem berechneten Vertauschungsfaktor. Die vierte Zeile ist die beste der bei der Brute-Force-Sitzung gefundenen Varianten, die auch in dem von der Comment-Funktion gezeichneten Chart dargestellt wird. Dieser Prototyp ist unten angehängt, damit Sie ihn testen können. Eigentlich kann er als Prototyp eines Handelsassistenten für den Tauschhandel dienen. Im Moment hat er noch wenig Funktionalität, aber ich werde versuchen, ihn im nächsten Artikel zu erweitern. Der Prototyp wird in zwei Versionen vorgestellt: für MetaTrader 4 und MetaTrader 5.
Schlussfolgerungen aus den ersten Tests
Es ist ziemlich schwierig, bei einem so komplexen Thema allein irgendwelche Schlussfolgerungen zu ziehen. Dennoch ist es mir gelungen, etwas Nützliches zu verstehen, obwohl ich bisher keinen Swap-Faktor größer als eins finden konnte. Dies sind die ersten Schlussfolgerungen, zu denen ich bei der Analyse der Arbeit dieses Prototyps gekommen bin:
- Für einige Währungspaare können Sie positive Swaps erhöhen oder negative reduzieren (aufgrund der Darstellung der Position als synthetisches Äquivalent).
- Selbst wenn kein profitabler Kreislauf gefunden wird, kann einer seiner Teile immer als alternative Position verwendet werden - zum Locking auf zwei verschiedenen Handelskonten.
- Beim Locking mit einer solchen synthetischen Position entfällt die Notwendigkeit, Swap-Free-Konten zu verwenden, da sie einen entgegengesetzten positiven Swap an beiden Enden ermöglicht.
- Es ist notwendig, eine bessere eingehende Analyse mit den populärsten Brokern durchzuführen, wofür die Funktionserweiterung notwendig ist.
- Ich hoffe, dass ich beweisen kann, dass ein profitabler Swap-Faktor erreicht werden kann (was bis jetzt nur eine Vermutung ist).
- Swaps können einen kleinen aber stetigen Gewinn bringen, wenn sie klug eingesetzt werden.
Schlussfolgerung
Ich hoffe, dass dieser Ansatz für Sie interessant ist und dass er Denkanstöße liefern kann. Die Methode ist sehr schwer zu verstehen, aber sie setzt eigentlich ein einfaches Prinzip um: die Eröffnung zweier entgegengesetzter Positionen mit dem gleichen Volumen. Die bloße Eröffnung von zwei solchen entgegengesetzten Positionen erzeugt immer einen Verlust. Es gibt keinen Broker, der einen größeren positiven One-Way-Swap zusammen mit einem kleineren, negativen One-Way-Swap anbietet. Natürlich werden Sie niemals positive Swaps in beide Richtungen finden, denn das ist mathematisch unmöglich.
Ich werde die Details der zugrundeliegenden Mathematik nicht wiedergeben, da dies ein sehr umfangreiches Thema ist. Es ist besser, die Manifestationen dieser Mathematik zu nutzen. Durch die Anwendung der beschriebenen Methode ist es möglich, den Verlust zu reduzieren, der durch die Vertauschung bei der Positionsverriegelung entsteht. Sie können auch versuchen, eine Lücke in den Swap-Tabellen der Broker zu finden und das Locking mit einem positiven Gewinnfaktor (ein profitabler Gesamt-Swap aller Positionen) zu genießen — es ist ein risikofreier Handel, der nicht von Kursschwankungen abhängig ist.
Ich denke, dass die Swap-Handelsmethoden wirklich unterschätzt werden, da ein positiver Swap einen potentiellen Gewinn bietet. Die beschriebene Methode ist nur eine der möglichen Varianten der Swap-Trading-Methoden, aber mir gefällt diese Aufgabe und ich werde versuchen, sie in den nächsten Artikeln fortzusetzen, indem ich die Idee weiterentwickle, den Code modernisiere und neue zusätzliche Funktionen schaffe. Ich werde auch einige Ideen bezüglich der Gewinnprognose und der Handelsfunktionalität beschreiben.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/9198
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Tipps von einem professionellen Programmierer (Teil II): Speichern und Austauschen von Parametern zwischen einem Expert Advisor, Skripten und externen Programmen
Tipps von einem professionellen Programmierer (Teil II): Speichern und Austauschen von Parametern zwischen einem Expert Advisor, Skripten und externen Programmen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Swaps (Teil I): Locking und synthetische Positionen wurde veröffentlicht:
Autor: Evgeniy Ilin
Vielen Dank für Ihre Artikel.
Ich danke Ihnen für Ihre Artikel.
Sie sind die willkommene ).
Hallo,
Ich habe den Experten sowohl auf MT4 als auch auf MT5 laufen lassen. Wenn es ein PostFix gibt, wird der Experte nicht laufen und keine Ergebnisse liefern.
Können Sie herausfinden, warum oder es beheben?
Vielen Dank!