
Swaps (Partie 1) : Verrouillage et Positions Synthétiques
Table des Matières
- Introduction
- À propos des Swaps
- Verrouillage à l'aide de deux comptes de trading
- À propos des Taux de Change
- Verrouillage à l'aide de positions synthétiques
- Écrire un Utilitaire pour Utiliser Swap Polygons
- Conclusions des Premiers Tests
- Conclusion
Introduction
J'ai longtemps réfléchi au sujet de cet article, mais je n'ai pas eu le temps d'effectuer une recherche détaillée. Le sujet des swaps est très répandu sur le web, principalement parmi les professionnels du trading qui comptent chaque pip, ce qui est en fait la meilleure approche du trading. Dans cet article, vous découvrirez comment utiliser les swaps à bon escient et vous verrez que les swaps doivent toujours être pris en compte. L'article présente également une idée très complexe mais intéressante sur la façon de moderniser les méthodes de trading des swaps. Ces méthodes (lorsqu'elles sont correctement préparées) peuvent être utilisées dans le cadre d'un seul compte ou comme outil d'amélioration des bénéfices dans le cadre d'un verrouillage classique utilisant deux comptes.
À propos des Swaps
Je n'expliquerai pas l'idée des swaps et leur théorie. Je ne m'intéresse qu'à l'application pratique des swaps. La question la plus importante est de savoir s'il est possible de réaliser des bénéfices grâce aux swaps. Du point de vue du trader, un swap est un gain ou une perte. De nombreux traders l'ignorent également tout simplement parce qu'ils s'en tiennent au trading intra-journalier. D'autres essaient de ne pas y prêter attention, pensant que c'est tellement insignifiant que cela ne peut guère affecter le trading. En fait, près de la moitié de l'écart peut être caché dans le swap. Ce spread n'est pas pris au moment de l'achat ou de la vente, mais lorsque le jour change sur le serveur.
Le swap est facturé par rapport au volume de la position ouverte. Cela se produit aux moments suivants :
- Du lundi au mardi
- Du mardi au mercredi
- Du mercredi au jeudi (presque tous les courtiers facturent un triple échange cette nuit-là)
- Du jeudi au vendredi
En général, la valeur du swap est indiquée dans la spécification de l'instrument de trading en points ou en pourcentage. Il peut y avoir d'autres méthodes de calcul, mais je n'ai réussi à en comprendre que deux, ce qui est bien suffisant. Il existe très peu d'informations structurées sur les swaps. Mais si vous étudiez la question, vous pouvez même trouver des stratégies efficaces basées sur les swaps. Ils génèrent un pourcentage de profit minime, mais ils ont un grand avantage : le profit est absolument garanti. La principale difficulté de cette approche réside dans le fait que les courtiers les plus populaires proposent très peu d'instruments avec un swap positif, et qu'il est donc très difficile de gagner de l'argent avec cette idée. Même le bénéfice potentiel est extrêmement faible. Mais cela vaut mieux que de perdre complètement votre dépôt. Et si vous utilisez un autre système de trading, vous le perdrez très probablement.
L'essentiel de mes conclusions concernant les opérations de change est que rien ne peut garantir un profit, à l'exception des swaps positifs. Il existe bien sûr des systèmes capables de générer des bénéfices. Mais en les utilisant, nous acceptons de payer notre argent au courtier pour toute opération de trading, et nous espérons que le prix évoluera dans la bonne direction. Un swap positif est le processus inverse. Je considère les déclarations suivantes comme les marqueurs d'un trading dans le sens positif du swap :
- Un swap positif équivaut à un mouvement partiel du prix vers notre position ouverte (profit chaque jour).
- Au bout d'un certain temps, un swap peut couvrir les pertes sur les écarts et les commissions ; au bout d'un certain temps, le swap ajoutera de l'argent
- Pour que le swap fonctionne, la position doit être maintenue aussi longtemps que possible, afin que le facteur de profit de cette position soit maximal.
- S'il est développé de manière approfondie, le bénéfice sera absolument prévisible et garanti.
Bien sûr, le principal inconvénient de cette approche est la dépendance à l'égard de la taille du dépôt. Mais aucun autre concept n'est capable de garantir avec autant d'assurance les bénéfices sur le Forex. Cette dépendance peut être réduite en diminuant le volume des positions ouvertes ou le risque (ce qui revient au même). Le risque est le rapport entre le volume de la position et le dépôt : une augmentation du volume de la position accroît le risque que le prix s'oriente dans la direction opposée et que le dépôt ne soit pas suffisant pour nous permettre d'attendre que les bénéfices des swaps compensent les pertes dues aux écarts et aux commissions. Un mécanisme de verrouillage a été inventé pour minimiser l'influence de tous les effets négatifs possibles.
Verrouillage à l'aide de deux comptes de trading
Cette méthode de swap est la plus populaire parmi les traders. Pour mettre en œuvre cette stratégie, vous aurez besoin de deux comptes avec des swaps différents pour les mêmes paires de devises ou d'autres actifs. Ouvrir deux positions opposées sur le même compte n'a pas de sens - cela équivaut à perdre purement et simplement le dépôt. Même si un symbole a un swap positif, ce swap sera négatif lorsqu'il sera négocié dans la direction opposée. Le schéma suivant illustre le concept de cette méthode :
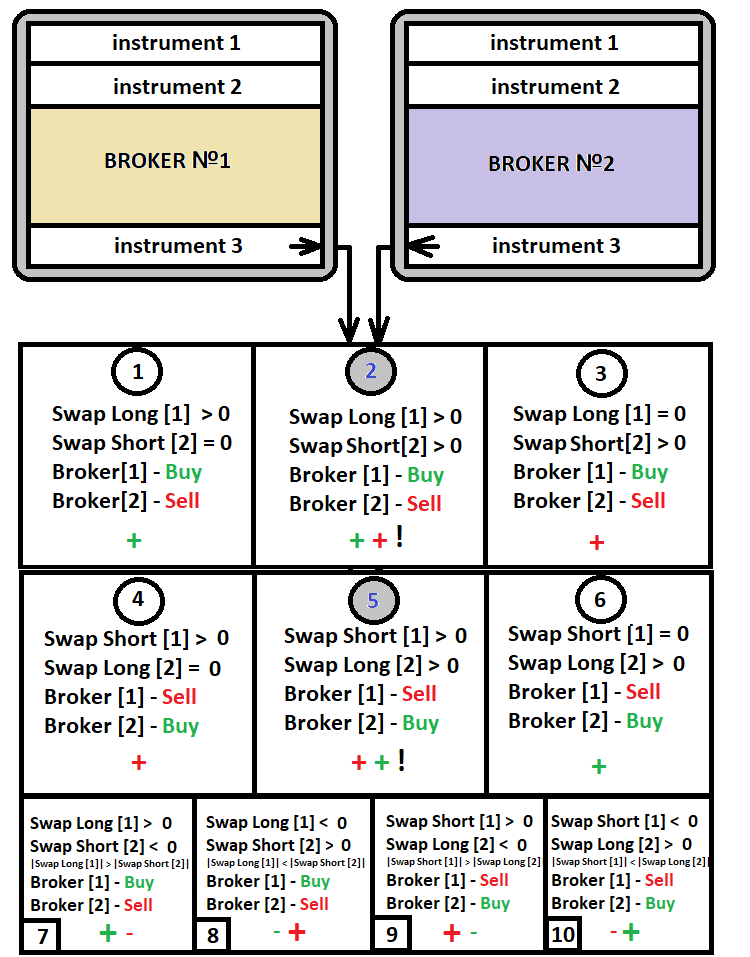
Comme le montre le diagramme, il n'existe que 10 scénarios de trading pour un instrument spécifiquement sélectionné pour lequel nous voulons négocier des swaps, dont 6 sont activement utilisés. Les quatre dernières options peuvent être choisies en dernier recours, s'il est impossible de trouver une paire de devises répondant aux conditions "1-6", car l'un des swaps est négatif. Il est possible de tirer profit du swap positif qui est supérieur au swap négatif. Vous pouvez trouver tous les cas mentionnés ci-dessus si vous analysez différents courtiers et leurs tables de swap. Mais les meilleures options pour cette stratégie sont "2" et "5". Ces options sont assorties de swaps positifs aux deux extrémités. Les deux courtiers réalisent donc des bénéfices. Et vous n'avez pas besoin de transférer des fonds entre les comptes aussi souvent.
Le principal inconvénient de cette stratégie est que vous devez toujours transférer de l'argent entre les comptes, car lorsque vous ouvrez des positions opposées, vous aurez des pertes avec un courtier et des bénéfices avec un autre courtier. Mais si vous calculez correctement les volumes de transactions par rapport au dépôt existant, vous n'aurez pas besoin de déplacer des fonds trop souvent. Il y a un avantage indiscutable : dans tous les cas, il y aura un bénéfice, et il est possible de prévoir l'ampleur exacte de ce bénéfice. Je pense que de nombreux utilisateurs préféreraient éviter cette routine et effectuer ces manipulations au sein d'un même compte (ce qui est impossible). Mais il existe une méthode permettant d'augmenter les bénéfices de la méthode classique de trading par swap, même si elle ne permet pas de négocier sur un seul compte. Examinons les principales caractéristiques de cette méthode.
À propos des Taux de Change
Commençons par la base même sur laquelle toute logique est construite. Des équations mathématiques peuvent être construites sur cette base. Prenons par exemple l'EURUSD, l'USDJPY et l'EURJPY. Ces trois paires sont corrélées. Pour comprendre cette relation, présentons ces symboles sous une forme légèrement différente :
- 1/P = EUR/USD
- 1/P = USD/JPY
- 1/P = EUR/JPY
- P est le taux de la devise sélectionnée
Tout instrument de trading comporte une devise (ou un actif équivalent) que l'on acquiert et une autre devise que l'on donne en échange. Par exemple, si vous prenez le premier ratio (paire EURUSD), lorsque vous ouvrez une position d'achat de 1 lot, vous acquérez 100 000 unités de la devise de base. Voici les règles du trading sur le Forex : un lot est toujours égal à 100 000 unités de la devise de base. La devise de base de cette paire est l'EUR. Nous achetons donc de l'EUR pour de l'USD. Dans ce cas, le taux de change "P" indique combien d'unités d'USD sont contenues dans 1 EUR. Il en va de même pour tous les autres symboles : la monnaie de base est contenue dans le numérateur, tandis que le dénominateur est la "monnaie principale" (si vous n'êtes pas d'accord avec cette dénomination, veuillez ajouter un commentaire ci-dessous). Le montant de la devise principale est calculé en multipliant simplement le prix par la valeur en euros :
- 1/P = EUR/USD ---> USD/P = EUR ---> USD = P*EUR
- EUR = Lots*100000
Lors de l'ouverture d'une position de vente, les devises changent de place. La monnaie de base commence à agir comme la monnaie principale, et la monnaie principale devient une monnaie de base. Autrement dit, nous achetons des USD contre des EUR, mais le montant des deux monnaies est calculé de la même manière — par rapport à l'EUR. C'est exact, car sinon il y aurait beaucoup de confusion. Les calculs sont les mêmes pour les autres devises. Dans la suite du calcul, nous utiliserons donc le signe "+" pour la monnaie de base et le signe "-" pour la monnaie principale. Par conséquent, toute transaction est assortie d'un ensemble de deux nombres correspondants qui symbolisent ce que nous achetons et pour quoi nous l'achetons. Une autre interprétation est qu'il y a toujours une monnaie qui fait office de produit et une autre monnaie qui fait office de monnaie et que nous payons pour acheter le produit.
Si nous ouvrons plusieurs positions pour plusieurs instruments, il y aura plus de devises principales et supplémentaires, et nous aurons ainsi une sorte de position synthétique. Du point de vue de l'utilisation des swaps, une telle position synthétique est absolument inutile. Mais nous pouvons créer une telle position synthétique qui sera très utile. Je le montrerai un peu plus tard. J'ai déterminé le calcul du volume exprimé par deux devises. Sur cette base, nous pouvons conclure que nous pouvons créer une position synthétique complexe qui sera équivalente à une position plus simple :
- EUR/JPY = EUR/USD * USD/JPY — taux de change composé de deux dérivés
Il existe en réalité un nombre infini de ces ratios, qui sont composés de plusieurs monnaies, telles que :
- EUR - Euro de l’Union Européenne
- USD - Dollar américain
- JPY - Yen japonais
- GBP - Livre sterling
- CHF - Franc suisse
- CAD - Dollar canadien
- NZD - Dollar néo-zélandais
- AUD - Dollar australien
- CNY - Yuan chinois
- SGD - Dollar de Singapour
- NOK - Couronne norvégienne
- SEK - Couronne suédoise
La liste des monnaies n'est pas exhaustive. Ce qu'il faut savoir, c'est qu'un instrument de trading arbitraire peut être composé de n'importe quelle devise de cette liste. Certains de ces instruments de trading sont proposés par des courtiers, alors que d'autres peuvent être obtenus en combinant des positions sur d'autres instruments. La paire EURJPY en est un exemple typique. Il ne s'agit là que de l'exemple le plus simple de composition de taux de change dérivés. Mais à partir de cette idée, nous pouvons conclure que toute position peut être présentée comme un ensemble de positions pour d'autres instruments. Il s'avère donc que :
- Valeur1 est la devise du symbole de base exprimée par une valeur absolue
- Valeur2 est la devise d’un symbole supplémentaire exprimée par une valeur absolue
- A est le volume du lot de la devise de base de la position
- B est le volume du lot de la devise principale de la position
- Le contrat est le montant de la devise achetée ou vendue en valeur absolue (correspond à 1 lot).
- A = 1/P = Valeur1/Valeur2 - c'est l'équation de tout instrument de trading (y compris ceux qui ne sont pas présentés dans la fenêtre du Market Watch).
- Valeur1 = Contrat*A
- Valeur2 = Contrat*B
Nous aurons besoin de ces ratios plus tard pour calculer les lots. Pour l'instant, ne les oubliez pas. Ces ratios décrivent le rapport entre le nombre de devises achetées ou vendues. Une logique de code plus sérieuse peut être construite sur cette base.
Verrouillage à l'aide de positions synthétiques
Dans cet article, une position synthétique est une position qui peut être composée à partir de plusieurs autres positions, alors que ces autres positions doivent nécessairement être composées d'autres instruments. Cette position doit être équivalente à une position ouverte pour n'importe quel instrument. Cela vous semble compliqué ? Mais en fait, c'est très simple. Une position de type peut être nécessaire pour :
- Bloquer la position initiale sur un instrument de trading simulé
- Essayer de créer l'équivalent d'une position avec des taux de swap complètement différents.
- D’autres objectifs
Voici le schéma général de cette méthode :
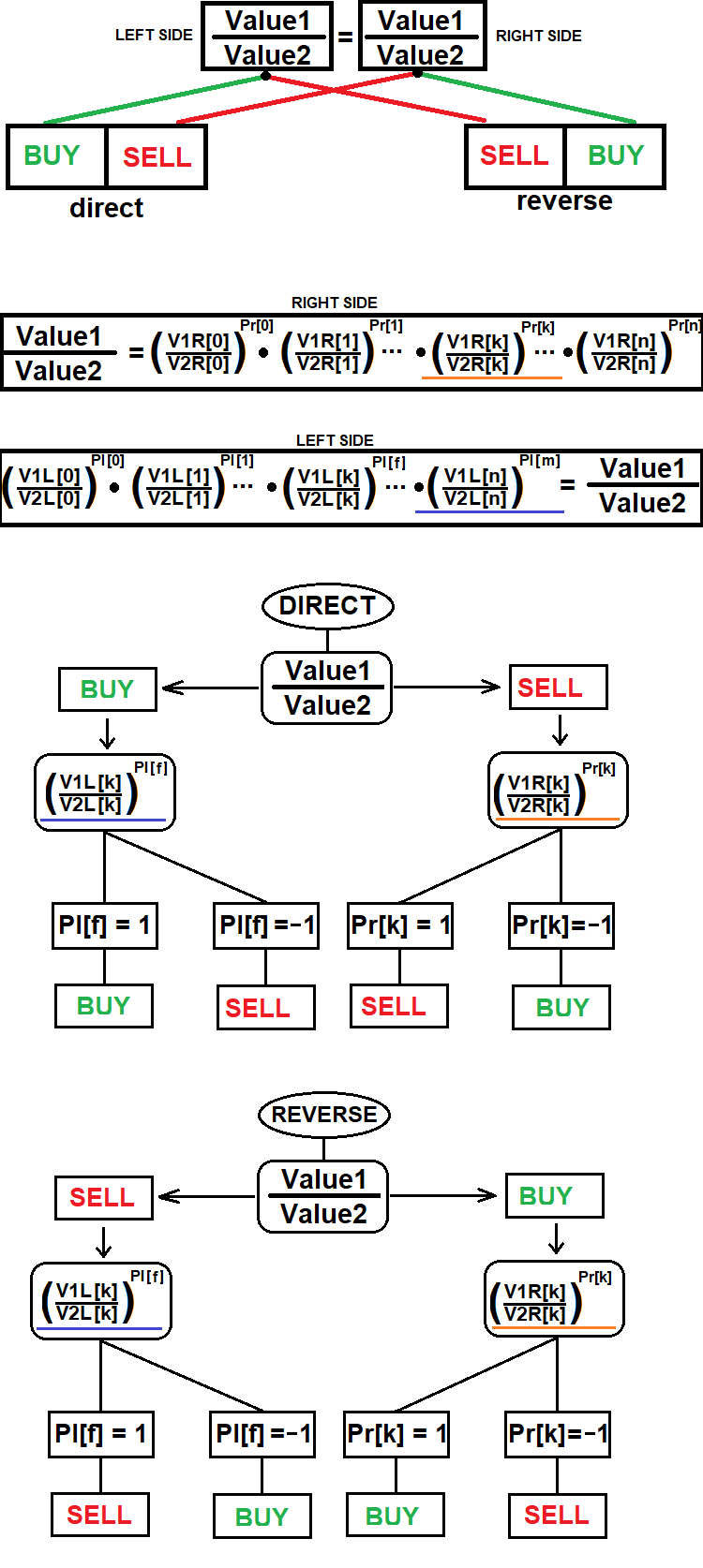
Même ce schéma ne couvre pas l'ensemble des données relatives à l'ouverture d'une position synthétique. Ce diagramme montre uniquement comment déterminer la direction des transactions pour un composant spécifique d'une position synthétique, qui doit nécessairement être représenté par l'un des instruments disponibles du courtier.
Il faut maintenant déterminer comment calculer les volumes de ces positions. Logiquement, les volumes devraient être calculés en considérant que la position devrait être équivalente à 1 lot de la position pour l'instrument résultant, à laquelle la variante sélectionnée de l'équation est réduite. Les valeurs suivantes sont nécessaires pour le calcul du volume :
- ContratB - la taille du contrat de la paire à laquelle l'équation est réduite (dans la plupart des cas, elle est égale à 100 000 unités de la devise de base).
- Contrat[1] - la taille du contrat de la paire pour laquelle vous voulez déterminer le lot
- A[1] - le montant de la devise de base exprimé en lots de la paire équilibrée précédente (ou la première de la chaîne)
- B[1] - le montant de la devise principale exprimé en lots de la paire équilibrée précédente (ou la première de la chaîne)
- A[2] - le montant de la devise de base exprimé en lots de la paire courante en cours d'équilibrage
- B[2] - le montant de la devise principale exprimé en lots de la paire courante en cours d'équilibrage
- C[1] - la taille du contrat de la paire équilibrée précédente (ou la première de la chaîne)
- C[2] - la taille du contrat de la paire en cours d'équilibrage
Veuillez noter qu'il n'est pas toujours possible de déterminer "ContratB", car l'instrument résultant de la combinaison peut ne pas être fourni par le courtier. Dans ce cas, le contrat peut être fixé arbitrairement, par exemple, égal à la constante de base "100 000".
La première paire de la chaîne est d’abord déterminée. Elle contient la devise de base de l'instrument résultant dans la position souhaitée. Ensuite, d'autres paires sont recherchées pour compenser les devises supplémentaires qui ne sont pas incluses dans l'équivalent obtenu. L'équilibrage se termine lorsque la devise principale est dans la bonne position dans la paire actuelle. J'ai créé un diagramme pour montrer comment cela se passe :
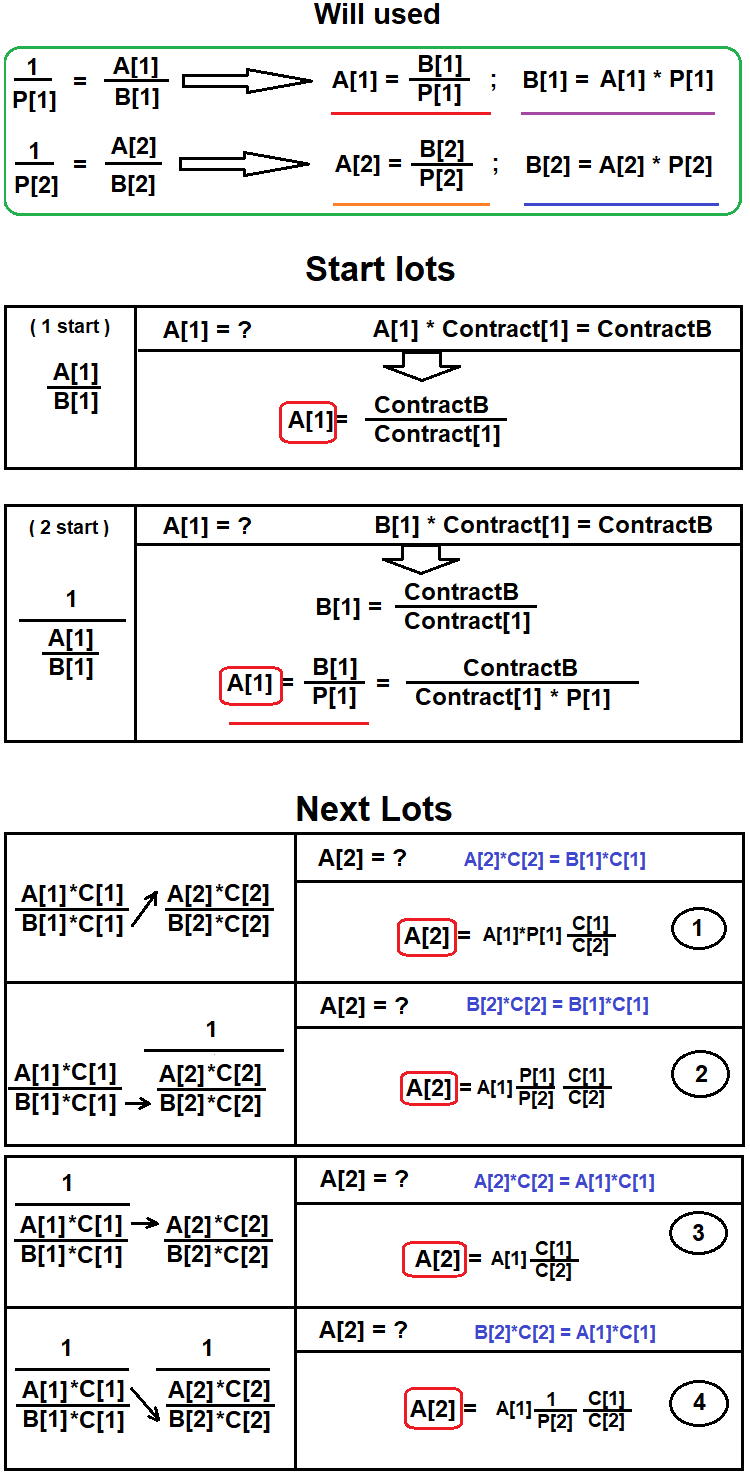
Mettons maintenant en œuvre ces techniques dans le code et analysons les résultats. Le premier prototype sera très simple, car son seul objectif est d'évaluer la justesse des idées. J'espère que les diagrammes ci-dessus vous aideront à comprendre tous les détails.
Écriture d’un Utilitaire pour Examiner les Polygones de Swaps
Tri et préparation des données du Market Watch
Pour utiliser cette technique, il est nécessaire de sélectionner uniquement les paires dont les noms comportent exactement 6 caractères et ne sont composés que de lettres majuscules. Je pense que tous les courtiers adhèrent à cette règle de dénomination. Certains courtiers ajoutent des préfixes ou des postfixes, qui doivent également être pris en compte lors de l'écriture d'algorithmes pour travailler avec des données de type chaîne de caractères. Afin de stocker les informations relatives aux symboles dans un format pratique, j'ai créé 2 structures (la seconde sera utilisée ultérieurement) :
struct Pair// required symbol information { string Name;// currency pair double SwapBuy;// buy swap double SwapSell;// sell swap double TickValue;// profit from 1 movement tick of a 1-lot position double TickSize;// tick size in the price double PointX;// point size in the price double ContractSize;// contract size in the base deposit currency double Margin;// margin for opening 1 lot }; struct PairAdvanced : Pair// extended container { string Side;// in numerator or denominator double LotK;// lot coefficient double Lot;// lot };
Certains champs ne seront pas utilisés lors du tri des paires. Afin de ne pas produire de conteneurs inutiles, je l'ai légèrement agrandi pour que la structure puisse également être utilisée à d'autres fins. J'avais le prototype d'un algorithme similaire, mais avec des capacités très limitées : il ne pouvait prendre en compte que les paires qui se trouvaient dans la fenêtre principale du terminal. Aujourd'hui, tout est plus simple. Plus important encore, toutes les opérations sont automatisées dans l'algorithme. La fonction suivante est nécessaire pour définir la taille du tableau d'instruments :
Pair Pairs[];// data of currency pairs void SetSizePairsArray()// set size of the array of pairs { ArrayResize(Pairs,MaxSymbols); ArrayResize(BasicPairsLeft,MaxPairs*2); // since each pair has 2 currencies, there can be a maximum of 2 times more base currencies ArrayResize(BasicPairsRight,MaxPairs*2);// since each pair has 2 currencies, there can be a maximum of 2 times more base currencies }
La première ligne fixe le nombre maximum de paires de la fenêtre du Market Watch que nous pouvons utiliser. Les deux autres lignes définissent la taille des tableaux qui seront utilisés. Les deux autres tableaux jouent un rôle auxiliaire : ils permettent de diviser une paire de devises en 2 parties (2 devises composées). Les variables surlignées en jaune sont les paramètres d'entrée de l'EA.
- MaxSymbols - la taille maximale de stockage des paires (j'ai implémenté une spécification manuelle)
- MaxPairs - le nombre maximum de paires dans les deux parties de la formule que nous générons (les formules plus longues que ce nombre ne seront pas recherchées par l'Expert Advisor).
Afin de vérifier si un instrument de trading répond aux critères (signes de deux devises différentes qui peuvent être potentiellement présents dans d'autres instruments), j'ai créé la fonction prédicat suivante :
bool IsValid(string s)// checking the instrument validity (its name must consist of upper-case letters) { string Mask="abcdefghijklmnopqrstuvwxyz1234567890";// mask of unsupported characters (lowercase letters and numbers) for ( int i=0; i<StringLen(s); i++ )// reset symbols { for ( int j=0; j<StringLen(Mask); j++ ) { if ( s[i] == Mask[j] ) return false; } } return true; }
Cette fonction n'est pas la seule condition pour les futurs contrôles des instruments. Mais cette condition ne peut pas être écrite dans une expression logique. Il est donc plus facile de l'implémenter sous la forme d'un prédicat. Passons maintenant à la fonction principale qui remplit le tableau avec les données nécessaires :
void FillPairsArray()// fill the array with required information about the instruments { int iterator=0; double correction; int TempSwapMode; for ( int i=0; i<ArraySize(Pairs); i++ )// reset symbols { Pairs[iterator].Name=""; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { TempSwapMode=int(SymbolInfoInteger(Pairs[iterator].Name,SYMBOL_SWAP_MODE)); if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) && SymbolInfoInteger(SymbolName(i,false),SYMBOL_TRADE_MODE) == SYMBOL_TRADE_MODE_FULL && ( ( TempSwapMode == 1 ) || ( ( TempSwapMode == 5 || TempSwapMode == 6 ) && CorrectedValue(Pairs[iterator].Name,correction) )) ) { if ( iterator >= ArraySize(Pairs) ) break; Pairs[iterator].Name=SymbolName(i,false); Pairs[iterator].TickSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_SIZE); Pairs[iterator].PointX=SymbolInfoDouble(Pairs[iterator].Name, SYMBOL_POINT); Pairs[iterator].ContractSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_CONTRACT_SIZE); switch(TempSwapMode) { case 1:// in points Pairs[iterator].SwapBuy=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); Pairs[iterator].SwapSell=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); break; case 5:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; case 6:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; } Pairs[iterator].Margin=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_MARGIN_INITIAL); Pairs[iterator].TickValue=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_VALUE); iterator++; } } }
Cette fonction permet une itération simple sur tous les symboles et un filtrage par une condition composée complexe qui vérifie à la fois le respect de l'exigence de longueur du nom de la chaîne et la possibilité de négocier ce symbole, ainsi que d'autres paramètres, qui concernent les symboles pour lesquels la méthode de calcul du swap diffère de la méthode la plus couramment utilisée "en points". L'une des méthodes de calcul du swap est sélectionnée dans le bloc "switch". Deux méthodes sont actuellement mises en œuvre : en points et en pourcentage. Un tri correct est essentiel pour éviter les calculs inutiles. Faites également attention à la fonction surlignée en rouge. Lorsque la monnaie principale (pas la monnaie de base) est représentée par une monnaie qui ne correspond pas à la monnaie de dépôt, un certain facteur d'ajustement doit être ajouté pour convertir le swap en monnaie de dépôt. Cette fonction calcule les bonnes valeurs. Voici le code :
bool CorrectedValue(string Pair0,double &rez)// adjustment factor to convert to deposit currency for the percentage swap calculation method { string OurValue=AccountInfoString(ACCOUNT_CURRENCY);// deposit currency string Half2Source=StringSubstr(Pair0,PrefixE+3,3);// lower currency of the pair to be adjusted if ( Half2Source == OurValue ) { rez=1.0; return true; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) )//find the currency rate to convert to the account currency { string Half1=StringSubstr(SymbolName(i,false),PrefixE,3); string Half2=StringSubstr(SymbolName(i,false),PrefixE+3,3); if ( Half2 == OurValue && Half1 == Half2Source ) { rez=SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } if ( Half1 == OurValue && Half2 == Half2Source ) { rez=1.0/SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } } } return false; }
Cette fonction sert de prédicat et renvoie la valeur du facteur d'ajustement à la variable qui a été transmise de l'extérieur par référence. Le facteur d'ajustement est calculé sur la base du taux de la devise souhaitée, qui inclut notre devise de dépôt.
Formules générées de manière aléatoire
Supposons que le tableau ait été rempli avec les données nécessaires. Nous devons maintenant itérer sur ces symboles et essayer de créer, à la volée, toutes les combinaisons possibles de formules qui peuvent être créées à partir de ces paires. Tout d'abord, il est nécessaire de décider sous quelle forme la formule sera stockée. La structure qui stocke tous les éléments de cette formule doit être très simple et claire pour les utilisateurs au cas où il serait nécessaire de consulter les journaux (ce qui sera certainement le cas, sinon il sera impossible d'identifier les erreurs).
Notre formule est un ensemble de facteurs à gauche et à droite du signe "=". Le facteur peut être le taux de change à la puissance 1 ou -1 (ce qui équivaut à une fraction inversée, ou à une unité référencée au taux de l'instrument actuel). J'ai décidé d'utiliser la structure suivante :
struct EquationBasic // structure containing the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula };
Toutes les données seront stockées sous forme de chaîne de caractères. Pour étudier la formule, ces chaînes seront analysées afin d'en extraire toutes les informations nécessaires. Elles peuvent également être affichées à tout moment. Les formules générées seront écrites sous la forme suivante :
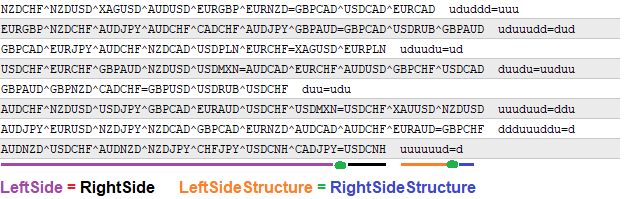
Pour moi, cet enregistrement est absolument clair et lisible. Le caractère "^" est utilisé comme séparateur entre les paires. Aucun séparateur n'est nécessaire dans la structure de la formule, puisqu'elle se compose des seuls caractères "u" et "d", qui indiquent le degré du multiplicateur :
- "u" est le taux de change
- "d" est 1/taux de change
Comme vous pouvez le voir, les formules résultantes ont une longueur et une taille variables des deux côtés de l'équation. Mais cette taille a ses limites. Cette approche permet d'obtenir une variabilité maximale des formules générées. Cela permet de garantir la meilleure qualité possible des variantes proposées dans les conditions de trading du courtier sélectionné. Les courtiers offrent des conditions totalement différentes. Pour garantir la réussite de la génération de ces formules, nous avons besoin de fonctions aléatoires supplémentaires capables de générer des nombres dans l'intervalle requis. Pour cela, créons la fonctionnalité en utilisant les capacités de la fonction MathRand intégrée :
int GenerateRandomQuantityLeftSide()// generate a random number of pairs on the left side of the formula { int RandomQuantityLeftSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-1))); if ( RandomQuantityLeftSide >= MaxPairs ) return MaxPairs-1; return RandomQuantityLeftSide; } int GenerateRandomQuantityRightSide(int LeftLenght)// generate a random number of pairs on the right side of the formula (taking into account the number of pairs on the left side) { int RandomQuantityRightSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-LeftLenght))); if ( RandomQuantityRightSide < 2 && LeftLenght == 1 ) return 2;// there must be at least 2 pairs in one of the sides, otherwise it will be equivalent to opening two opposite positions if ( RandomQuantityRightSide > (MaxPairs-LeftLenght) ) return (MaxPairs-LeftLenght); return RandomQuantityRightSide; } int GenerateRandomIndex()// generate a random index of a symbol from the MarketWatch window { int RandomIndex=0; while(true) { RandomIndex=int(MathFloor((double(MathRand())/32767.0) * double(MaxSymbols)) ); if ( RandomIndex >= MaxSymbols ) RandomIndex=MaxSymbols-1; if ( StringLen(Pairs[RandomIndex].Name) > 0 ) return RandomIndex; } return RandomIndex; }
Ces 3 fonctions seront nécessaires à un moment donné. Nous pouvons maintenant écrire la fonction qui générera ces formules. Le code deviendra de plus en plus complexe, mais je n'utiliserai pas d'approche orientée objet, car la tâche n'est pas standard. J'ai décidé d'utiliser une approche procédurale. Les procédures qui en résultent sont assez volumineuses et encombrantes. Mais il n'y a pas de fonctionnalité supplémentaire. Chaque fonction met en œuvre une tâche spécifique sans utiliser de fonctions intermédiaires, afin d'éviter la duplication du code. Sinon, le code serait encore plus difficile à comprendre en raison des spécificités de la tâche. La fonction se présente comme suit :
EquationBasic GenerateBasicEquation()// generate both parts of the random equation { int RandomQuantityLeft=GenerateRandomQuantityLeftSide(); int RandomQuantityRight=GenerateRandomQuantityRightSide(RandomQuantityLeft); string TempLeft=""; string TempRight=""; string TempLeftStructure=""; string TempRightStructure=""; for ( int i=0; i<RandomQuantityLeft; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == 0 && RandomQuantityLeft > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i != 0 && (RandomQuantityLeft-i) > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft-1 ) TempLeft+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempLeftStructure+="u"; else TempLeftStructure+="d"; } for ( int i=RandomQuantityLeft; i<RandomQuantityLeft+RandomQuantityRight; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == RandomQuantityLeft && RandomQuantityRight > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i != RandomQuantityLeft && (RandomQuantityLeft+RandomQuantityRight-i) > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft+RandomQuantityRight-1 ) TempRight+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempRightStructure+="u"; else TempRightStructure+="d"; } EquationBasic result; result.LeftSide=TempLeft; result.LeftSideStructure=TempLeftStructure; result.RightSide=TempRight; result.RightSideStructure=TempRightStructure; return result; }
Comme vous pouvez le constater, les 3 fonctions considérées précédemment sont utilisées ici pour générer une formule aléatoire. Ces fonctions ne sont utilisées nulle part ailleurs dans le code. Dès que la formule est prête, nous pouvons procéder à une analyse étape par étape de cette formule. Toutes les formules incorrectes seront éliminées par le prochain filtre complexe extrêmement important. Tout d'abord, vérifiez l'égalité. Si les parties ne sont pas égales, cette formule est incorrecte. Toutes les formules conformes passent à l'étape suivante de l'analyse.
Équilibrage de la formule
Cette étape couvre plusieurs critères d'analyse à la fois :
- Compter tous les facteurs supplémentaires au numérateur et au dénominateur et les supprimer
- Vérification de la disponibilité d'une devise au numérateur et d'une devise au dénominateur
- Vérification de la correspondance des fractions obtenues à gauche et à droite
- Si le côté droit est la réciproque du côté gauche, il suffit d'inverser la structure droite de la formule (ce qui revient à élever à la puissance "-1").
- Si toutes les étapes sont franchies avec succès, le résultat est écrit dans une nouvelle variable.
Voici comment ces étapes apparaissent dans le code :
BasicValue BasicPairsLeft[];// array of base pairs to the left BasicValue BasicPairsRight[];// array of base pairs to the right bool bBalanced(EquationBasic &CheckedPair,EquationCorrected &r)// if the current formula is balanced (if yes, return the corrected version to the "r" variable) { bool bEnd=false; string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } //// Calculate balance values for the left side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(CheckedPair.LeftSide,i,1); if ( Divider == "^" || i == StringLen(CheckedPair.LeftSide) - 1 ) { SubPair=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of left-side balance calculation //// Calculate balance values for the right side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(CheckedPair.RightSide,i,1); if ( Divider == "^"|| i == StringLen(CheckedPair.RightSide) - 1 ) { SubPair=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.RightSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of right-side balance calculation /// calculate the number of lower and upper currencies based on the received data from the previous block int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpLeft; string LastDownLeft; string LastUpRight; string LastDownRight; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity > 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[i].Quantity; if ( BasicPairsLeft[i].Quantity < 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[i].Quantity; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity > 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightUpTotal+=BasicPairsRight[i].Quantity; if ( BasicPairsRight[i].Quantity < 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightDownTotal-=BasicPairsRight[i].Quantity; } /// /// check if both sides are equal if ( LeftUpTotal == 1 && LeftDownTotal == 1 && RightUpTotal == 1 && RightDownTotal == 1 )// there must be one pair in the upper and in the lower part of both sides of the equality, otherwise the formula is invalid { for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity == 1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastUpLeft=BasicPairsLeft[i].Value; if ( BasicPairsLeft[i].Quantity == -1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastDownLeft=BasicPairsLeft[i].Value; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity == 1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastUpRight=BasicPairsRight[i].Value; if ( BasicPairsRight[i].Quantity == -1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastDownRight=BasicPairsRight[i].Value; } } else return false; if ( (LastUpLeft == LastUpRight && LastDownLeft == LastDownRight) || (LastUpLeft == LastDownRight && LastDownLeft == LastUpRight) ) { if ( LastUpLeft == LastDownRight && LastDownLeft == LastUpRight )// If the formula is cross-equivalent, then invert the structure of the right part of the equation (it is the same as raising to the power of -1) { string NewStructure;// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; } } else return false;// if the resulting fractions on both sides are not equivalent, then the formula is invalid if ( LastUpLeft == LastDownLeft ) return false;// if result in one, then the formula is invalid /// Now it is necessary to write all the above into a corrected and more convenient structure string TempResult=CorrectedResultInstrument(LastUpLeft+LastDownLeft,r.IsResultInstrument); if ( r.IsResultInstrument && LastUpLeft+LastDownLeft != TempResult ) { string NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.LeftSideStructure); i++ ) { if ( CheckedPair.LeftSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.LeftSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.LeftSideStructure=NewStructure; r.ResultInstrument=LastDownLeft+LastUpLeft; r.UpPair=LastDownLeft; r.DownPair=LastUpLeft; } else { r.ResultInstrument=LastUpLeft+LastDownLeft; r.UpPair=LastUpLeft; r.DownPair=LastDownLeft; } r.LeftSide=CheckedPair.LeftSide; r.RightSide=CheckedPair.RightSide; r.LeftSideStructure=CheckedPair.LeftSideStructure; r.RightSideStructure=CheckedPair.RightSideStructure; /// /// if code has reached this point, it is considered that we have found the formula meeting the criteria, and the next step is normalization return true; }
La fonction surlignée en vert est nécessaire pour déterminer si la liste des symboles contient celle à laquelle la formule a été réduite. Il se peut que la formule ait été réduite, par exemple, non pas à "USDJPY", mais à "JPYUSD". Ce symbole n'existe évidemment pas, même s'il peut être créé. Mais notre tâche consiste à modifier la formule pour qu'elle produise un instrument de trading correct. Dans ce cas, les deux parties de la formule doivent être élevées à la puissance -1, ce qui revient à inverser la structure de la formule (remplacer "d" par "u" et vice versa). Si ce symbole n'existe pas dans la fenêtre du Market Watch, laissez-le tel quel :
string CorrectedResultInstrument(string instrument, bool &bResult)// if any equivalent symbol corresponds to the generated formula, return this symbol (or leave as is) { string Half1=""; string Half2=""; string Half1input=StringSubstr(instrument,0,3);//input upper currency string Half2input=StringSubstr(instrument,3,3);//input lower currency bResult=false; for ( int j=0; j<ArraySize(Pairs); j++ ) { Half1=StringSubstr(Pairs[j].Name,PrefixE,3); Half2=StringSubstr(Pairs[j].Name,PrefixE+3,3); if ( (Half1==Half1input && Half2==Half2input) || (Half1==Half2input && Half2==Half1input) )// direct match or crossed match { bResult=true; return Pairs[j].Name; } } return instrument; }
J'ai préparé la structure suivante pour stocker les formules qui ont passé le filtre. La structure comprend certains champs de la structure précédente et de nouveaux champs :
struct EquationCorrected // corrected structure of the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula string ResultInstrument;// the resulting instrument to which both parts of the formula come after transformation bool IsResultInstrument;// has the suitable equivalent symbol been found string UpPair;// the upper currency of the resulting instrument string DownPair;// the lower currency of the resulting instrument };
Normalisation des Formules
Cette procédure constitue l'étape suivante du filtrage des résultats. Elle se compose des opérations séquentielles suivantes, qui se succèdent l'une après l'autre :
- Sur la base du symbole obtenu des deux côtés de l'équation, sélectionnez une paire de départ dans la liste pour les deux côtés de l'égalité.
- Les deux paires, selon leur puissance dans l'équation, doivent fournir la devise de base dans le numérateur de la fraction
- Si une telle paire est trouvée, et que la devise inférieure de la fraction ne contient pas la devise principale de l'instrument résultant, il faut aller plus loin.
- Nous allons plus loin de sorte que la devise supérieure de la paire suivante compense la devise inférieure de la paire précédente.
- Répétez ces étapes jusqu'à ce que la paire résultante souhaitée soit trouvée
- Une fois la paire obtenue, tous les composants inutilisés de la formule sont éliminés (puisque leur produit est 1).
- Parallèlement à ce processus, les "lot factors" sont calculés séquentiellement d'une paire à l'autre (ils indiquent le lot nécessaire pour ouvrir des positions pour des paires spécifiques, afin de garantir l'instrument résultant).
- Le résultat est inscrit dans une nouvelle variable, qui sera utilisée lors de l'étape suivante de l'analyse.
Le code de la fonction est le suivant :
bool bNormalized(EquationCorrected &d,EquationNormalized &v)// formula normalization attempt (the normalized formula is returned in "v" ) { double PreviousContract;// previous contract bool bWasPairs;// if any pairs have been found double BaseContract;// contract of the pair to which the equation is reduced double PreviousLotK=0.0;// previous LotK double LotK;// current LotK string PreviousSubSide;// in numerator or denominator (previous factor) string PreviousPair;// previous pair string PreviousHalf1;// upper currency of the previous pair string PreviousHalf2;// lower currency of the previous pair string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity int tryiterator=0;// the number of balancing attempts int quantityleft=0;// the number of pairs on the left after normalization int quantityright=0;//the number of pairs on the right after normalization bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } if ( d.IsResultInstrument ) BaseContract=SymbolInfoDouble(d.ResultInstrument, SYMBOL_TRADE_CONTRACT_SIZE);// define the contract of the equivalent pair based on the instrument else BaseContract=100000.0; //// Calculate the number of pairs for the left side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.LeftSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } /// end of quantity calculation for the left part ArrayResize(v.PairLeft,tryiterator); /// calculate the lot coefficients for the left side bool bBalanced=false;// is the formula balanced bool bUsed[]; ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); int balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false;// have there been pairs for ( int k=0; k<tryiterator; k++ )// try to normalize the left side { if( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" || i == StringLen(d.LeftSide) - 1 ) { SubPair=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 1 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 2 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 3 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 4 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } v.PairLeft[balancediterator].Name=SubPair; v.PairLeft[balancediterator].Side=SubSide; v.PairLeft[balancediterator].ContractSize=SymbolInfoDouble(v.PairLeft[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityleft++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part string LastUpLeft; string LastDownLeft; for ( int z=0; z<ArraySize(BasicPairsLeft); z++ ) { if ( BasicPairsLeft[z].Quantity > 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[z].Quantity; if ( BasicPairsLeft[z].Quantity < 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[z].Quantity; } if ( bWasPairs && LeftUpTotal == 0 && LeftDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } /// end of coefficient calculation for the left part if ( !bBalanced ) return false;// if the left side is not balanced, then there is no point in balancing the right side //// Calculate the number of pairs for the right side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.RightSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } ArrayResize(v.PairRight,tryiterator); /// end of calculation of the number of pairs for the right side bBalanced=false;// is the formula balanced ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false; for ( int k=0; k<tryiterator; k++ )// try to normalize the right side { if ( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" || i == StringLen(d.RightSide) - 1 ) { SubPair=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.RightSideStructure,quantityiterator,1); Half1=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.RightSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (1) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (2) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (3) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (4) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } v.PairRight[balancediterator].Name=SubPair; v.PairRight[balancediterator].Side=SubSide; v.PairRight[balancediterator].ContractSize=SymbolInfoDouble(v.PairRight[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityright++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpRight; string LastDownRight; for ( int z=0; z<ArraySize(BasicPairsRight); z++ ) { if ( BasicPairsRight[z].Quantity > 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightUpTotal+=BasicPairsRight[z].Quantity; if ( BasicPairsRight[z].Quantity < 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightDownTotal-=BasicPairsRight[z].Quantity; } if ( bWasPairs && RightUpTotal == 0 && RightDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } if ( quantityleft == 1 && quantityright == 1 ) return false;// if the equation has been normalized to only 2 pairs, it is not valid (at least 3 pairs are required) return bBalanced; }
Il s'agit d'une procédure très saine et complexe. Mais il me semble que dans de tels cas, il est préférable de ne pas produire d'états intermédiaires, car cela entraînera une duplication importante du code. Toutes les étapes sont également très compactes et sont logiquement divisées en blocs. L'ensemble de ces fonctions nous donne des résultats absolument identiques et comparables aux résultats que nous pourrions obtenir en effectuant toutes les conversions à la main. Ici, toutes ces manipulations mathématiques sont effectuées par un ensemble de méthodes complexes mais nécessaires.
Nous devons effectuer une analyse spéciale pour comprendre la rentabilité de la formule trouvée. N'oubliez pas que pour chaque paire, il est possible d'ouvrir une position à la hausse comme à la baisse. En conséquence, il peut y avoir deux variantes intermédiaires de circuits pour chaque formule - directe et inversée. Celle dont la rentabilité est la plus élevée sera retenue comme résultat.
Pour évaluer la rentabilité, j'ai créé un indicateur similaire au facteur de profit, qui se compose des profits et des pertes résultant des swaps. Si le swap positif accumulé du circuit existant est supérieur au module négatif, ce circuit est considéré comme rentable. Dans d'autres cas, ces circuits ne sont pas rentables - en d'autres termes, le facteur swap de notre contour ne sera positif que s'il est supérieur à 1.
Le résultat renvoyé est écrit dans un conteneur complètement différent, qui a été créé comme un ensemble de commandes autonomes pour le trading et pour le développement ultérieur de la logique de trading. Il contient tout ce qui est nécessaire pour ouvrir rapidement et facilement l'ensemble du circuit :
struct EquationNormalized // the final structure with the formula in normalized form { Pair PairLeft[];// currency pairs on the left side Pair PairRight[];// currency pairs on the right side double SwapPlusRelative;// relative equivalent of the positive swap double SwapMinusRelative;// relative equivalent of the negative swap double SwapFactor;// resulting swap factor };
J'ai également ajouté 2 méthodes qui permettent l'affichage des informations sur le contenu. Mais elles ne sont pas pertinentes pour cet article et je ne les fournirai donc pas ici. Vous pouvez les voir dans le code source ci-joint. Désormais, les informations relatives à chaque composante de l'équation sont contenues séparément en tant qu'éléments de tableaux. Cela permet de travailler plus facilement avec les données par la suite sans avoir à les analyser constamment à partir de chaînes de caractères. Cette solution pourrait peut-être être utilisée dès le début, mais cela aurait nui à la lisibilité.
Calcul du facteur de swap et ajustement final de la structure de l'équation
Il s'agit de la dernière étape, au cours de laquelle la variable la plus importante de ce système est calculée - les variantes seront comparées en fonction de cette valeur. Celle qui a la valeur la plus élevée est la meilleure.
void CalculateBestVariation(EquationNormalized &ii)// calculation of the best swap factor of the formula and final structure adjustment if needed { double SwapMinus=0.0;// total negative swap double SwapPlus=0.0;// total positive swap double SwapMinusReverse=0.0;// total negative swap double SwapPlusReverse=0.0;// total positive swap double SwapFactor=0.0;// swap factor of the direct pass double SwapFactorReverse=0.0;// swap factor of the reverse pass for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// define the missing parameters for calculating the left side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairLeft[i].Name ) { ii.PairLeft[i].Margin=Pairs[j].Margin; ii.PairLeft[i].TickValue=Pairs[j].TickValue; ii.PairLeft[i].SwapBuy=Pairs[j].SwapBuy; ii.PairLeft[i].SwapSell=Pairs[j].SwapSell; break; } } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// define the missing parameters for calculating the right side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairRight[i].Name ) { ii.PairRight[i].Margin=Pairs[j].Margin; ii.PairRight[i].TickValue=Pairs[j].TickValue; ii.PairRight[i].SwapBuy=Pairs[j].SwapBuy; ii.PairRight[i].SwapSell=Pairs[j].SwapSell; break; } } } double TempSwap; // calculate all components taking into account a change in the structure for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// for left parts { if ( ii.PairLeft[i].Side == "u" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairLeft[i].Side == "d" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// for right parts { if ( ii.PairRight[i].Side == "d" ) {// for direct trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairRight[i].Side == "u" ) {// for direct trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } // calculate the swap factor for the direct pass if ( SwapMinus > 0.0 && SwapPlus > 0.0 ) SwapFactor=SwapPlus/SwapMinus; if ( SwapMinus == 0.0 && SwapPlus == 0.0 ) SwapFactor=1.0; if ( SwapMinus == 0.0 && SwapPlus > 0.0 ) SwapFactor=1000001.0; if ( SwapMinus > 0.0 && SwapPlus == 0.0 ) SwapFactor=0.0; // calculate the swap factor for the reverse pass if ( SwapMinusReverse > 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=SwapPlusReverse/SwapMinusReverse; if ( SwapMinusReverse == 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=1.0; if ( SwapMinusReverse == 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=1000001.0; if ( SwapMinusReverse > 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=0.0; // select the best approach and calculate the missing values in the structure if ( SwapFactor > SwapFactorReverse ) { ii.SwapPlusRelative=SwapPlus; ii.SwapMinusRelative=SwapMinus; ii.SwapFactor=SwapFactor; } else { ii.SwapPlusRelative=SwapPlusReverse; ii.SwapMinusRelative=SwapMinusReverse; ii.SwapFactor=SwapFactorReverse; bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// if it is a reverse pass, then reverse the right structure of the formula { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } bSigned=false; for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// if it is a reverse pass, then reverse the left structure of the formula { bSigned=false; if ( !bSigned && ii.PairLeft[i].Side == "u" ) { ii.PairLeft[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairLeft[i].Side == "d" ) { ii.PairLeft[i].Side="u"; bSigned=true; } } } bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// reverse the right side anyway { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } }
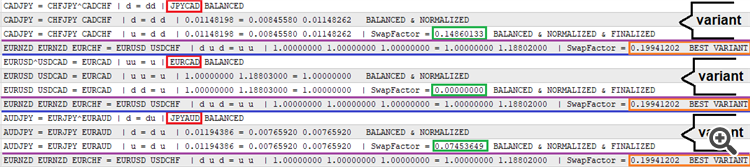
Pour permettre la sortie séquentielle du résultat, j'ai implémenté le journal qui n'est écrit que si la variante de formule filtrée avec succès est trouvée. Le journal est le suivant :
La couleur rouge est utilisée pour le symbole résultant, auquel les deux côtés de l'équation sont réduits. La ligne suivante montre la variante normalisée avec les coefficients de lot. La troisième ligne montre la variante avec le facteur de swap calculé. La quatrième ligne est la meilleure des variantes trouvées au cours de la session de force brute, qui est également représentée sur le graphique tracé avec la fonction Comment. Le prototype est attaché ci-dessous, afin que vous puissiez le tester. En fait, il peut servir de prototype d'assistant de trading pour les opérations de swap. Pour l'instant, il n'a que peu de fonctionnalités, mais j'essaierai de l'étendre dans le prochain article. Le prototype est présenté en 2 versions : pour MetaTrader 4 et pour MetaTrader 5.
Conclusions des Premiers Tests
Il est difficile de tirer des conclusions sur un sujet aussi complexe. Mais j'ai réussi à comprendre quelque chose d'utile, bien que je n'aie pas été en mesure de trouver un facteur de swap supérieur à 1 jusqu'à présent. Telles sont les premières conclusions auxquelles j'ai abouti en analysant le travail de ce prototype :
- Pour certaines paires de devises, il est possible d'augmenter les swaps positifs ou de réduire les swaps négatifs (en raison de la présentation de la position en tant qu'équivalent synthétique).
- Même si un circuit rentable n'est pas trouvé, l'une de ses parties peut toujours être utilisée comme position alternative - pour le verrouillage sur 2 comptes de trading différents.
- Le verrouillage avec une telle position synthétique élimine la nécessité d'utiliser des comptes sans swap, puisqu'il permet d'avoir un swap positif opposé aux deux extrémités.
- Il est nécessaire d'effectuer de meilleures analyses approfondies avec les courtiers les plus populaires, pour lesquels l'extension des fonctionnalités est nécessaire.
- J'espère pouvoir prouver qu'un facteur de swap rentable peut être atteint (ce qui n'est pour l'instant qu'une supposition).
- Les swaps peuvent générer des bénéfices modestes mais réguliers s'ils sont utilisés à bon escient.
Conclusion
J'espère que cette approche est intéressante pour vous et qu'elle peut nourrir votre réflexion. La méthode est très difficile à comprendre, mais elle met en œuvre un principe simple : ouvrir 2 positions opposées avec le même volume. La simple ouverture de ces deux positions opposées génère toujours une perte. Il n'existe pas de courtier fournissant un swap à sens unique positif plus important en modulo qu'un swap à sens unique négatif. Bien entendu, vous ne trouverez jamais de swaps positifs dans les deux sens, car c'est mathématiquement impossible.
Je ne fournirai pas les détails des mathématiques sous-jacentes, car il s'agit d'un sujet très vaste. Il est préférable d'utiliser les manifestations de ces mathématiques. En appliquant la méthode décrite, il est possible de réduire la perte causée par le swap du verrouillage de position. Vous pouvez également essayer de trouver un écart dans les tableaux de swap des courtiers et profiter d'un verrouillage avec un facteur de profit positif (un swap total rentable de toutes les positions) - il s'agit d'un trading sans risque qui ne dépend pas des fluctuations de prix.
Je pense que les méthodes de swap sont vraiment sous-estimées, car un swap positif offre un potentiel de profit. La méthode décrite n'est qu'une des variations possibles des méthodes de swap trading. Mais j'aime cette tâche et j'essaierai de la poursuivre dans les prochains articles, en développant l'idée, en modernisant le code et en créant de nouvelles fonctionnalités supplémentaires. Je décrirai également quelques idées concernant les prévisions de bénéfices et les fonctionnalités de trading.
Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/9198
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Cet article a été rédigé par un utilisateur du site et reflète ses opinions personnelles. MetaQuotes Ltd n'est pas responsable de l'exactitude des informations présentées, ni des conséquences découlant de l'utilisation des solutions, stratégies ou recommandations décrites.
 Figures et exemples (partie I) : Multiple Top, ou Hauts Multiples
Figures et exemples (partie I) : Multiple Top, ou Hauts Multiples
 Développer un Expert Advisor de trading à partir de zéro (partie 31) : Vers l'avenir (IV)
Développer un Expert Advisor de trading à partir de zéro (partie 31) : Vers l'avenir (IV)
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Un nouvel article intitulé Swaps (Part I) : Locking et positions synthétiques a été publié :
Auteur : Evgeniy Ilin
Merci pour vos articles.
Merci pour vos articles.
Vous êtes le bienvenu ).
Bonjour,
J'ai lancé l'expert sur MT4 et MT5, lorsqu'il y a un PostFix, l'expert ne s'exécute pas et n'obtient aucun résultat.
Pouvez-vous trouver la raison de ce problème ou le résoudre ?
Merci beaucoup.