掉期利率（第一部分）：锁定与合成仓位

内容目录

• 概述
• 关于掉期利率
• 利用两个交易账户互锁
• 关于汇率
• 利用合成仓位锁定
• 编写实用程序来使用多边掉期利率
• 第一次测试的结论
• 结束语

概述

这篇文章的题目我已思考了很久，但一直没时间深入详细研究。 掉期利率的话题在网络上十分广泛，主要在那些计算每个点的交易专业人士当中，这实际上是最好的交易方法。 从本文中，您将发现如何针对商品使用掉期利率，并将看到必须始终考虑到掉期利率。 此外，本文还提供了一个非常复杂但有趣的思路，如何令掉期利率交易方法与时俱进。 这种方法（如若准备得当）可以在一个账户中使用，也可用两个账户达成经典的利润锁定强化工具。

关于掉期利率

我不会解释掉期利率的思路及其原理。 我仅对掉期利率的实际应用感兴趣。 最重要的问题在于是否有可能通过掉期利率赚取利润。 以交易者的观点来说，掉期利率要么盈利、亦或亏损。 甚或，许多坚持日内交易的交易者都忽略了它。 其他人也尽量不去关注它，认为它微不足道，很难对交易产生影响。 而事实上，几乎一半的点差隐藏在掉期利率之中。 这个点差不是在买卖时收取的，而是在服务器上日期变更时计算的。

掉期利率是相对于持仓量来收取的。 它会发生在以下时刻：

1. 周一到周二
2. 周二到周三
3. 从周三到周四（几乎所有经纪商都会在这晚收取三倍掉期利率）
4. 周四到周五

通常，掉期利率的数值在交易工具规范中以点数或百分比表示。 可以有其他的计算方法，但我只设法理解了其中的两种，这已经足够了。 关于掉期利率的结构化信息很少。 然而，如果您研究这个问题，您甚至可能会发现一些基于掉期利率的有效策略。 它们产生的利润百分比很小，但它们有一个极大的优势 — 利润绝对有保障。 这种方式的主要困难在于，事实上大多数受欢迎的经纪商仅提供少数的具有正掉期利率的金融产品，因此很难按照这种思路赚钱。 甚至可能的潜在利润也极低。 尽管如此，这总比彻底爆仓要好。 如果您正采用任何其他交易系统，您很可能会把本金亏光。 

关于外汇交易的结论，我的底线是，除了正掉期利率之外，没啥能保证盈利。 当然，有一些系统能够产生利润。 然而，在使用它们时，我们同意向经纪商支付任何交易操作的费用，并且我们希望价格朝着正确的方向发展。 正掉期利率是逆过程。 以下陈述是我理解的按照正掉期利率进行交易的标志：

• 正掉期利率等价于部分价格朝我们的持仓方向移动（每天都有盈利）
• 一段时间后，掉期利率可以弥补点差和佣金的损失；而此后，掉期利率会令资金增加
• 为了令掉期利率见效，持仓时间应尽可能长，那么这笔持仓的盈利因子将是最大化
• 如果开发得彻底，利润绝对可预测和有保障

当然，这种方式的最大缺点是依赖存款规模，但没有其他有如此自信的概念能够保证在外汇市场盈利。 这种依赖性可通过减少持仓量或风险来降低（这其实是相同的）。 风险是持仓量与资金的比率：持仓量增加会令我们的风险同步增加，即价格也许会向亏损方向发展，而资金可能不足以令我们等到掉期利率的利润弥补点差/佣金的亏损。 为了尽量减少所有可能的负面影响，发明了一种锁定机制。

利用两个交易账户互锁

这种掉期利率交易方法在交易者中极受追捧。 为了实现此策略，您将需要两个账户，且对于相同的货币对或其他资产拥有不同的掉期利率。 在同一个账户内开立两笔互逆的持仓是没有意义的 — 这等价于轻易地令资金亏损。 即使其中一个品种的掉期利率为正，当按相反的方向交易时，这个掉期利率最终会为负值。 下图反映了这个方法的概念：

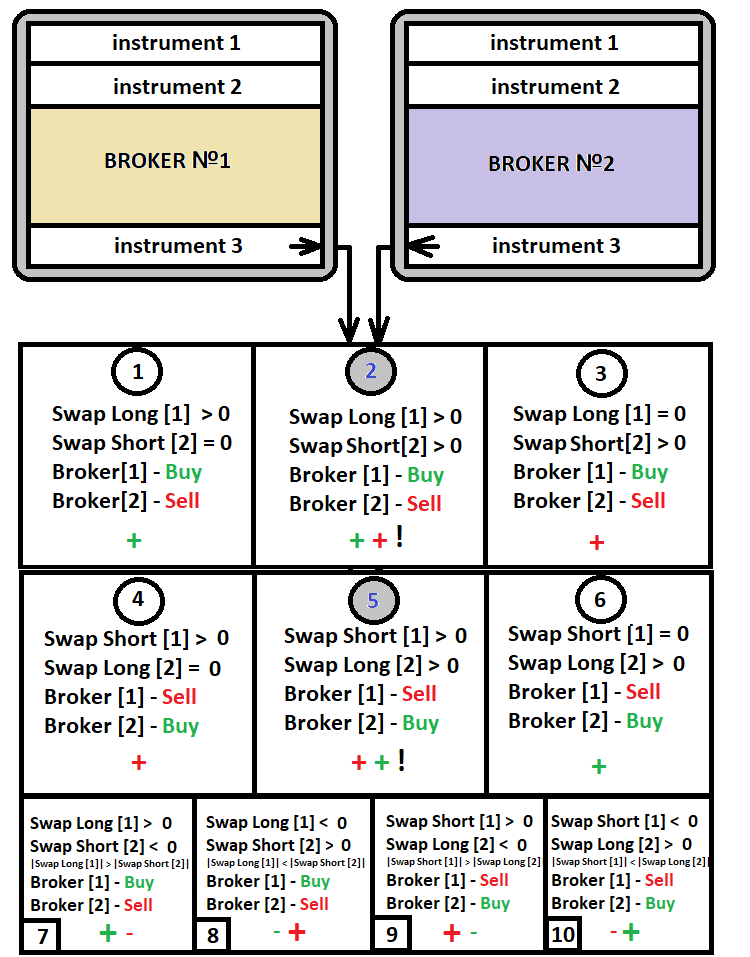
如您从图中所见，若我们想要进行掉期利率交易，那么针对所选的特定金融产品，只有 10 种交易场景，其中 6 个已被激活采用。 如果不能找到与条件 “1-6” 匹配的货币对，由于这里的掉期利率之一是负数，则可选择最后四个选项作为最终手段。 从正值大于负值的掉期利率中获利是可能的。 如果您分析不同的经纪商及其掉期利率表，您可以找到上述所有案例。 但此策略的最佳选择是 “2” 和 “5”。 这些选项在两端都拥有正掉期利率。 因此，利润是从两个经纪商那里赚来的。 甚至，您都不必经常在账户之间转移资金。

这种策略的主要缺点就是您仍然需要在账户之间转移资金，因为在开立互逆持仓时，您在一个经纪商处亏损，而在另一家经纪商处盈利。 然而，如果您正确计算依赖于现有资金的交易量，您就不必过于频繁地转移资金。 但它有个无可争辩的优势：无论如何都会有盈利，而这种盈利的确切规模是可预测的。 我认为许多用户更愿意避免这种例行任务，并以某种方式在一个帐户中执行这些操作（这是不可能的）。 但有一种方法可以提升经典掉期利率交易方法的利润，即使它不允许在一个账户内进行交易。 我们来讨论一下这种方法的主要特点。

关于汇率

我们从构建所有逻辑的基础开始。 在此基础上可以建立数学方程。 例如，参考 EURUSD、USDJPY、EURJPY。 所有这 3 个货币对都是相关联的。 为了能理解这种关系，我们以稍微不同的形式来表示这些品种：

• 1/P = EUR/USD
• 1/P = USD/JPY
• 1/P = EUR/JPY
• P 是所选货币的汇率

任何交易的金融产品都含有我们所需的一种货币（或某种等价资产），和作为我们回报提供的另一种货币。 例如，如果您采用第一个汇率（EURUSD 货币对），那么在开仓买入 1 手时，您将得到 100,000 单位的基准货币。 这是外汇交易规则：一手总是等于 100,000 单位的基准货币。 该货币对的基准货币是 EUR，因此我们以 USD 购买 EUR。 在这种情况下，货币汇率 “P” 表示 1 EUR 中包含多少 USD 单位。 这同样适用于所有其他品种：基准货币包含在分子中，而分母是“"主要货币”（如果您不同意此命名，请在下面添加评论）。 主要货币的金额简单地通过将价格乘以 EUR 数值来计算：

• 1/P = EUR/USD --->  USD/P = EUR ---> USD = P*EUR
• EUR = Lots*100000

开立空头仓位时，货币会改变位置。 基准货币开始充当主要货币，而原来的主要货币则变为基准货币。 换言之，我们以 EUR 买入 USD，但两种货币的金额以相同的方式计算 — 相对于 EUR。 这是正确的，否则会产生很多混乱。 其他货币的计算方法相同。 故此，我们在进一步计算中使用符号 “+” 代表基准货币，符号 “-” 代表主要货币。 结果就是，任何交易都有两个对应的一组数字，它们象征着我们以什么购买了什么。 对此的另一种解释是，总有一种货币作为产品，另一种货币作为货币，我们支付货币来购买产品。 

如果我们为若干个金融产品开立多必仓位，那么将会有更多的主要和附加货币，因此我们得到一组合成仓位。 从掉期利率的角度来看，这样的合成仓位是绝对无用的。 但我们可以创建这样一个合成仓位，令其有利于我们。 稍后我会展示它。 我已经测算了由两个货币表达的交易量计算。 有基于此，我们可得出结论，即我们可以创建一个复杂的合成仓位，等价于一笔简单的仓位：

• EUR/JPY = EUR/USD * USD/JPY — 汇率由两种衍生品组成

在现实中，这样的汇率有无数种，它们由若干种货币组成，例如：

• EUR - 欧盟欧元
• USD - 美元
• JPY - 日元
• GBP - 英镑
• CHF - 瑞郎
• CAD - 加元
• NZD - 新西兰元
• AUD - 澳元
• CNY - 人民币
• SGD - 新加坡元
• NOK - 挪威克朗
• SEK - 瑞典克朗

这并非完整的货币列表。 我们需要知道的是，任意交易的金融产品均可由该列表中的任意货币组成。 其中一些交易的金融产品由经纪商提供，而另一些交易的金融产品可由其他金融产品仓位组合而来。 一个典型的例子是 EURJPY 货币对。 这只是构成衍生品汇率的最简单示例，但依据这些思路，我们可以得出结论，任何仓位都可以表示为一组其他金融产品的仓位。 综上所述，得出结果：

• Value1 是用绝对值表示的基准符号货币
• Value2 是用绝对值表示的附加品种货币
• A 是基准货币的持仓手数
• B 是是主要货币的持仓手数
• Contract（合约）是购买或卖出货币的绝对值（对应 1 手）
• A = 1/P = Value1/Value2 - 它是任何交易的金融产品的方程（包括那些没有出现在市场观察窗口中的）
• Value1 = Contract*A
• Value2 = Contract*B

我们稍后将需要这些比率来计算手数。 至于现在，记住它们即可。 这些比率描述了买卖货币的数量之比。 在此基础上可以构建更严谨的代码逻辑。

利用合成仓位锁定

在本文中，合成仓位是可以由几个其他仓位组成的仓位，而这些其他仓位必须要由其他金融产品组成。 该仓位必须等价于一笔所有产品的持仓。 看起来很复杂？ 其实，这一切都非常简单。 这种仓位也许是为了某种需求：

1. 锁定模拟交易金融产品的原始持仓
2. 尝试创建等价于拥有完全不同掉期l利率的持仓
3. 其他目的

最初，我是针对第 2 点提出了这个思路。 经纪商出于不同目的而设置了掉期利率值，其主要目的是期望产生额外利润。 我认为经纪商也会考虑竞争对手的掉期利率，以防止交易者交易掉期利率泛滥。 下图解释了这一概念。 也许您可以强化此示意图。

这是该方法的通常策划：

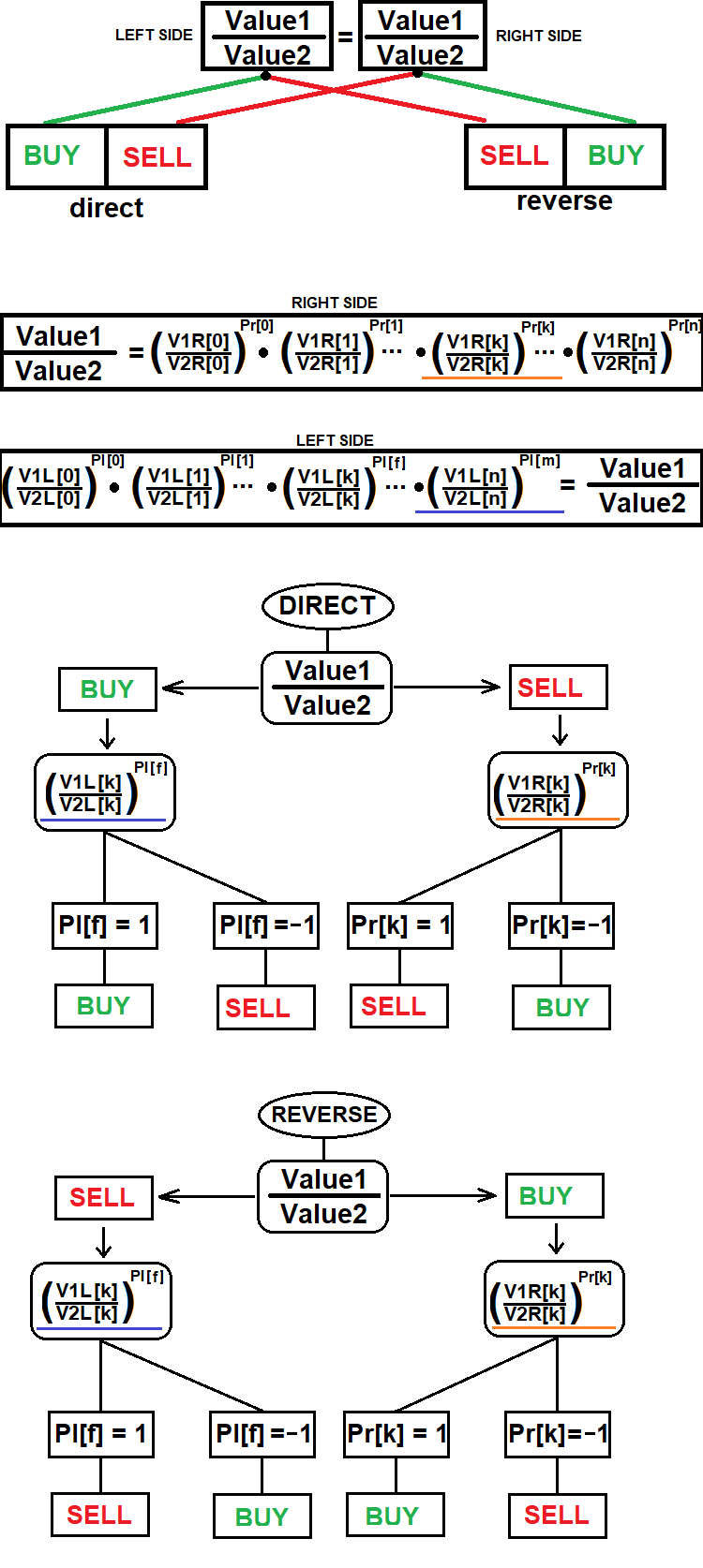
即使这个策划也并未涵盖有关如何开立合成仓位的全部数据。 该示意图仅展示如何判定一笔合成仓位的特定组件的交易方向，其必须由所选经纪商的可用金融产品之一来表示。 

现在，我们需要判定如何计算这些仓位的交易量。 逻辑上，交易量的计算应基于这样的考虑，即仓位应等同于所得金融产品的 1 手仓位，所选定的等式变体就会减少。 交易量计算需要以下值：

• ContractB - 需减少等式的货币对合约大小（在大多数情况下，它等于 100,000 单位的基准货币）
• Contract[1] - 您想要判定手数的货币对的合约大小
• A[1] - 基准货币的数量，它由前一个平衡（或链中的第一个）货币对的手数表达
• B[1] -  由前一个平衡（或链中的第一个）货币对的手数表达的主要货币数量
• A[2] -  由当前正在平衡的货币对的手数表达的基准货币数量
• B[2] - 由当前正在平衡的货币对的手数表达的主要货币数量
• C[1] - 前一个已平衡货币对（或链中的第一个）的合约大小
• C[2] - 当前正在平衡的货币对的合约大小

请注意，并非总是可以确定 “ContractB”，因为经纪商可能不提供组合产生的金融产品。 在这种情况下，合约可以任意设置，例如，等于基准常数 “100000”。

首先，判断链中的第一对，其会包含期望仓位的最终金融产品的基准货币。 然后，搜索其他货币对，来补偿未包含在最终等价物中的额外货币。 当主要货币在当前货币对中处于正确位置时，平衡结束。 我已创建了一个图表来展示这是如何做到的：

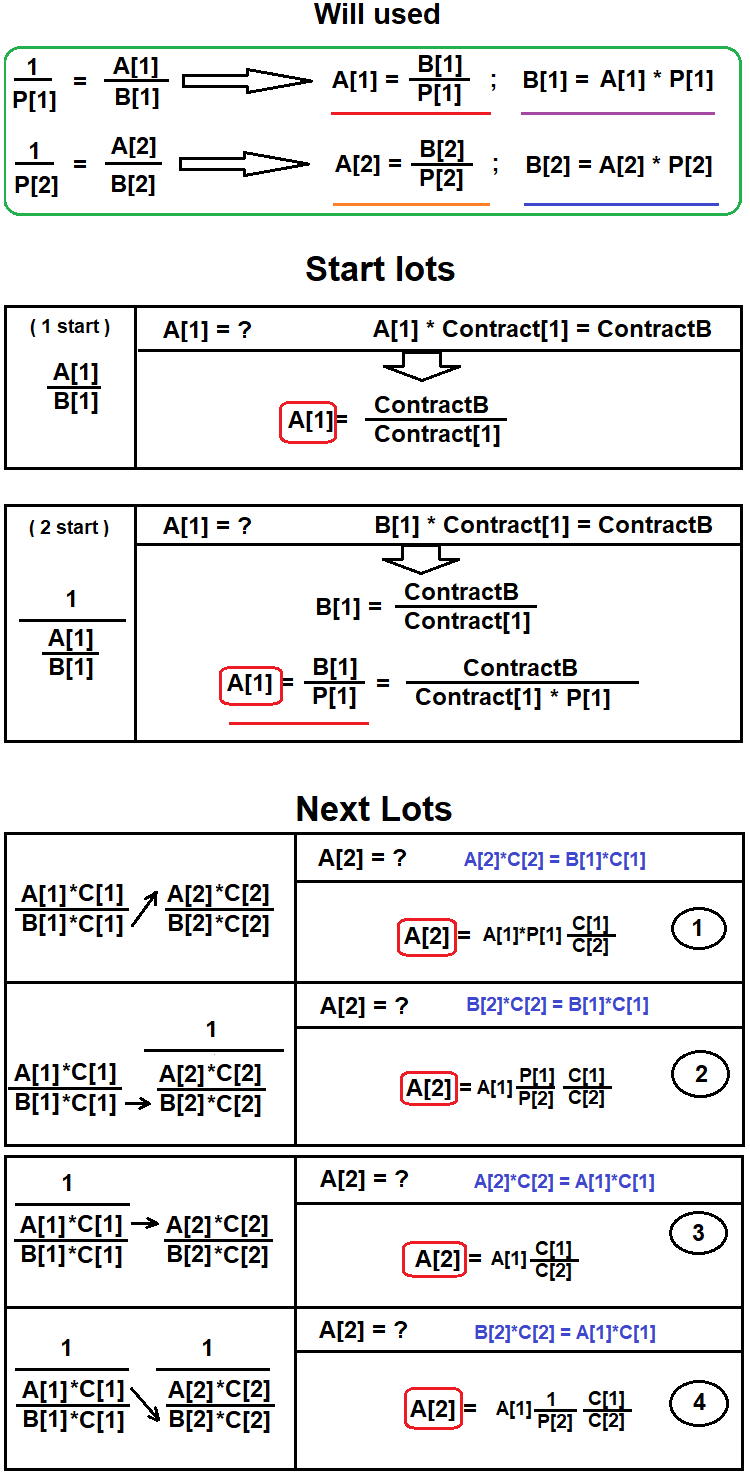
现在，我们在代码中实现这些技术，并分析结果。 第一个原型将非常简单，因为它的唯一目的是评估思路的正确性。 我希望上面的示意图能帮助您理解这个思路的所有细节。

编写一个实用工具来检验多边掉期利率

市场观察排序和数据准备：

为了运用该技术，选择的货币名称必须正好为 6 个字符长，且仅由大写字母组成。 我认为所有经纪商都会遵守这个命名规则。 一些经纪商加了前缀或后缀，在编写操控字符串数据的算法时，也应考虑到这些。 为了按照便捷的格式存储品种信息，我创建了两个结构（后面会用到第二个）：

struct Pair// required symbol information
   {
   string Name;// currency pair
   double SwapBuy;// buy swap
   double SwapSell;// sell swap
   double TickValue;// profit from 1 movement tick of a 1-lot position
   double TickSize;// tick size in the price
   double PointX;// point size in the price
   double ContractSize;// contract size in the base deposit currency
   double Margin;// margin for opening 1 lot
   };

struct PairAdvanced : Pair// extended container
   {
   string Side;// in numerator or denominator
   double LotK;// lot coefficient
   double Lot;// lot
   };

货币对排序时不会用到某些字段。 为避免产生非必要的容器，我已把它进行了一些扩展，从而也可拿该结构用于其他目的。 我有一个类似算法的原型，但功能非常有限：只能考虑将其用于主终端窗口中的那些货币对。 现在，一切都很简单了。 更重要的是，在算法中所有操作都是自动的。 为了设置金融产品数组的大小，需要以下函数：

Pair Pairs[];// data of currency pairs
void SetSizePairsArray()// set size of the array of pairs
   {
   ArrayResize(Pairs,MaxSymbols);
   ArrayResize(BasicPairsLeft,MaxPairs*2); // since each pair has 2 currencies, there can be a maximum of 2 times more base currencies
   ArrayResize(BasicPairsRight,MaxPairs*2);// since each pair has 2 currencies, there can be a maximum of 2 times more base currencies
   }

第一行设置从市场观察窗口中我们能取用的最大货币对数量。 另外两行设置操作用的数组大小。 剩余的 2 个数组扮演辅助作用 — 它们能够把货币对切分成 2 部分（2 个复合货币）。 以黄色高亮显示的变量是 EA 的输入参数。

• MaxSymbols - 最大货币对存储大小（我已实现了手动规范）
• MaxPairs - 按我们的公式生成的两个部分中的最大货币对数量（智能交易系统不会搜索长于该数字的公式）

为了检查交易的金融产品是否符合标准（两种不同货币的符号也可能存在于其他金融产品当中），我创建了以下断言函数：

bool IsValid(string s)// checking the instrument validity (its name must consist of upper-case letters)
   {
   string Mask="abcdefghijklmnopqrstuvwxyz1234567890";// mask of unsupported characters (lowercase letters and numbers)
   for ( int i=0; i<StringLen(s); i++ )// reset symbols
      {
      for ( int j=0; j<StringLen(Mask); j++ )
         {
         if ( s[i] == Mask[j] ) return false;
         }
      }   
   return true;
   }

此函数并非以后检查金融产品的唯一条件。 但这个条件不能写在逻辑表达式内部，所以它实现为断言更容易。 现在，我们进入为数组填充必要数据的主函数：

void FillPairsArray()// fill the array with required information about the instruments
   {
   int iterator=0;
   double correction;
   int TempSwapMode;
   
   for ( int i=0; i<ArraySize(Pairs); i++ )// reset symbols
      {
      Pairs[iterator].Name="";
      }   
   
   for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window
      {
      TempSwapMode=int(SymbolInfoInteger(Pairs[iterator].Name,SYMBOL_SWAP_MODE));
      if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) && SymbolInfoInteger(SymbolName(i,false),SYMBOL_TRADE_MODE) == SYMBOL_TRADE_MODE_FULL  
      && ( ( TempSwapMode  == 1 )  ||  ( ( TempSwapMode == 5 || TempSwapMode == 6 ) && CorrectedValue(Pairs[iterator].Name,correction) )) )
         {
         if ( iterator >= ArraySize(Pairs) ) break;
         Pairs[iterator].Name=SymbolName(i,false);
         Pairs[iterator].TickSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_SIZE);
         Pairs[iterator].PointX=SymbolInfoDouble(Pairs[iterator].Name, SYMBOL_POINT);
         Pairs[iterator].ContractSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_CONTRACT_SIZE);
         switch(TempSwapMode)
           {
            case  1:// in points
              Pairs[iterator].SwapBuy=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize);
              Pairs[iterator].SwapSell=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize);              
              break;
            case  5:// in percent
              Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);
              Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);              
              break;
            case  6:// in percent
              Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);
              Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0);              
              break;              
           }     
         Pairs[iterator].Margin=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_MARGIN_INITIAL);
         Pairs[iterator].TickValue=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_VALUE);         
         iterator++;
         }
      }
   }

此函数提供了所有品种的简单迭代，并按照复杂的复合条件进行过滤，它检查是否符合字符串名称长度要求，和该品种能否交易的可能性，以及其他参数，譬如与品种相关的，计算掉期利率方法里不同于最常用的“点数”。 在 “switch” 模块中选择一种掉期利率计算方法。 目前，有两种实现方法：点数和百分比。 正确的排序对于避免不必要的计算很重要。 另外，请注意红色高亮显示的函数。 当主要货币（非基准货币）由区别于存款货币的某个货币表示时，应加入一定的调整因子，从而将掉期利率转换到存款货币。 该函数计算相关值。 此处是它的代码：

bool CorrectedValue(string Pair0,double &rez)// adjustment factor to convert to deposit currency for the percentage swap calculation method
   {
   string OurValue=AccountInfoString(ACCOUNT_CURRENCY);// deposit currency
   string Half2Source=StringSubstr(Pair0,PrefixE+3,3);// lower currency of the pair to be adjusted
   if ( Half2Source == OurValue )
      {
      rez=1.0;
      return true;
      }
   
   for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window
      {
      if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) )//find the currency rate to convert to the account currency
         {
         string Half1=StringSubstr(SymbolName(i,false),PrefixE,3);
         string Half2=StringSubstr(SymbolName(i,false),PrefixE+3,3);
     
         if ( Half2 == OurValue && Half1 == Half2Source )
            {
            rez=SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID);
            return true;
            }
         if ( Half1 == OurValue && Half2 == Half2Source )
            {
            rez=1.0/SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID);
            return true;
            }            
         }
      } 
   return false;
   }

该函数作为断言，也会把调整因子值返回到由外部引用传递来的变量。 调整因子是依据所需货币的汇率计算得到的，其中包括我们的存款货币。

随机生成的公式

假设数组均已填充了必要的数据。 现在，我们需要以某种方式迭代这些品种，并尝试依据这些货币对动态创建所有可能的公式组合。 首先，必须决定以何种形式存储公式。 存储该公式所有元素的结构应该是非常简单和清晰的，可应对用户查看日志的需要（肯定会有这样的需求，否则无法识别错误）。

我们的公式是 “=” 符号左右两侧的一组因子。 该因子可以是货币汇率的 1 或 -1 次幂（相当于倒数，或指当前金融产品汇率的单位）。 我决定使用以下结构：

struct EquationBasic // structure containing the basic formula
   {
   string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign
   string LeftSideStructure;// structure of the left side of the formula
   string RightSide;// currency pairs participating in the right side of the formula
   string RightSideStructure;// structure of the right side of the formula
   };

所有数据均以字符串格式存储。 为了研究公式，将解析这些字符串，并提取我们所需的所有必要信息。 此外，它们可以在需要时打印。 生成的公式将按照以下格式打印：

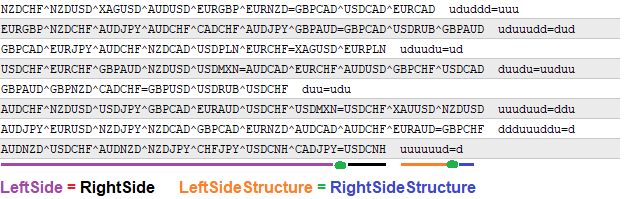
就我个人而言，这样的记录绝对清晰易读。 字符 "^" 用作货币对之间的分隔符。 公式结构中不需要分隔符，因为它由单个字符 "u" 和 "d", 组成，表示多重数的程度：

1. "u" 是货币汇率
2. "d" 是1 / 货币汇率（即倒数）

如您所见，得到的公式在等式两边都有一个浮动长度和一个浮动大小，但这个大小有其极限。 这种方式为生成的公式提供了最大可变性。 如此，反之，在所选经纪商的交易条件内，能发现变体可能的最高品质。 经纪商提供的条件完全不同。 为了确保这些公式能成功生成，我们需要额外的随机函数来生成所需范围内的数字。 为此目的，我们利用内置 MathRand 函数的能力创建相关功能：

int GenerateRandomQuantityLeftSide()// generate a random number of pairs on the left side of the formula
   {
   int RandomQuantityLeftSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-1)));
   if ( RandomQuantityLeftSide >= MaxPairs ) return MaxPairs-1;
   return RandomQuantityLeftSide;
   }

int GenerateRandomQuantityRightSide(int LeftLenght)// generate a random number of pairs on the right side of the formula (taking into account the number of pairs on the left side)
   {
   int RandomQuantityRightSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-LeftLenght)));
   if ( RandomQuantityRightSide < 2 && LeftLenght == 1 ) return 2;// there must be at least 2 pairs in one of the sides, otherwise it will be equivalent to opening two opposite positions
   if ( RandomQuantityRightSide > (MaxPairs-LeftLenght) ) return (MaxPairs-LeftLenght);
   return RandomQuantityRightSide;
   }
   
int GenerateRandomIndex()// generate a random index of a symbol from the MarketWatch window
   {
   int RandomIndex=0;
     
   while(true)
      {
      RandomIndex=int(MathFloor((double(MathRand())/32767.0) * double(MaxSymbols)) );
      if ( RandomIndex >= MaxSymbols ) RandomIndex=MaxSymbols-1;
      if ( StringLen(Pairs[RandomIndex].Name) > 0 ) return RandomIndex;
      }

   return RandomIndex;
   }

在某个阶段将需要所有这三个函数。 现在，我们能够编写生成这些公式的函数。 代码会变得越来越复杂，但我不会采用面向对象的方法，因为任务并非标准的。 我决定采用过程化方法。 由此产生的程序相当庞大和繁琐，但没有额外的功能，每个函数都执行特定的任务，无需任何中间函数，从而避免代码重复。 否则，由于任务规范，代码将更加难以理解。 该函数将如下所示：

EquationBasic GenerateBasicEquation()// generate both parts of the random equation
   {
   int RandomQuantityLeft=GenerateRandomQuantityLeftSide();
   int RandomQuantityRight=GenerateRandomQuantityRightSide(RandomQuantityLeft);
   string TempLeft="";
   string TempRight="";
   string TempLeftStructure="";
   string TempRightStructure="";   
   
   for ( int i=0; i<RandomQuantityLeft; i++ )
      {
      int RandomIndex=GenerateRandomIndex();
      if ( i == 0 && RandomQuantityLeft > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^";
      if ( i != 0 && (RandomQuantityLeft-i) > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^";
      if ( i == RandomQuantityLeft-1 ) TempLeft+=Pairs[RandomIndex].Name;
      
      if ( double(MathRand())/32767.0 > 0.5 ) TempLeftStructure+="u";
      else TempLeftStructure+="d";
      }
      
   for ( int i=RandomQuantityLeft; i<RandomQuantityLeft+RandomQuantityRight; i++ )
      {
      int RandomIndex=GenerateRandomIndex();
      
      if ( i == RandomQuantityLeft && RandomQuantityRight > 1 ) TempRight+=Pairs[RandomIndex].Name+"^";
      if ( i != RandomQuantityLeft && (RandomQuantityLeft+RandomQuantityRight-i) > 1 ) TempRight+=Pairs[RandomIndex].Name+"^";
      if ( i == RandomQuantityLeft+RandomQuantityRight-1 ) TempRight+=Pairs[RandomIndex].Name;
      
      if ( double(MathRand())/32767.0 > 0.5 ) TempRightStructure+="u";
      else TempRightStructure+="d";
      }
      
   EquationBasic result;
   result.LeftSide=TempLeft;
   result.LeftSideStructure=TempLeftStructure;
   result.RightSide=TempRight;
   result.RightSideStructure=TempRightStructure;
   
   return result;
   }

如您所见，为了生成随机公式，此处用到了先前研究的所有三个函数。 这些函数并未在代码中的其他任何地方用到。 一旦公式准备就绪，我们就可以逐步分析这个公式。 所有不正确的公式都将由下一个极其重要的复杂过滤器舍弃。 首先，检查是否等价。 如果某部分不等价，则此公式不正确。 所有符合的公式进入下一个分析步骤。

公式平衡

此步骤一次性涵盖多个分析准则：

1. 计算分子和分母中的所有额外因子并删除它们
2. 检查分子和分母中某种货币的可用性
3. 检查左右两边所得分子的对应关系
4. 如果右侧是左侧的倒数，我们只需将公式的右侧结构颠倒（类似于 “-1” 次幂）
5. 如果所有阶段都顺利完成，把结果写入一个新变量。

这些步骤在代码中如此出现：

BasicValue BasicPairsLeft[];// array of base pairs to the left
BasicValue BasicPairsRight[];// array of base pairs to the right
bool bBalanced(EquationBasic &CheckedPair,EquationCorrected &r)// if the current formula is balanced (if yes, return the corrected version to the "r" variable)
   {
   bool bEnd=false;
   string SubPair;// the full name of the currency pair
   string Half1;// the first currency of the pair
   string Half2;// the second currency of the pair
   string SubSide;// the currency pair in the numerator or denominator
   string Divider;// separator
   int ReadStartIterator=0;// reading start index
   int quantityiterator=0;// quantity
   bool bNew;
   BasicValue b0;
   
   for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs 
      {
      BasicPairsLeft[i].Value = "";
      BasicPairsLeft[i].Quantity = 0;
      }
   for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs
      {
      BasicPairsRight[i].Value = "";
      BasicPairsRight[i].Quantity = 0;
      }
   //// Calculate balance values for the left side
   quantityiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(CheckedPair.LeftSide); i++ )// extract base currencies from the left side of the equation
      {
      Divider=StringSubstr(CheckedPair.LeftSide,i,1);
      if ( Divider == "^" || i == StringLen(CheckedPair.LeftSide) - 1 )
         {
         SubPair=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,6);
         SubSide=StringSubstr(CheckedPair.LeftSideStructure,quantityiterator,1);
         Half1=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,3);
         Half2=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE+3,3);         

         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsLeft[j].Value == Half1 )
               {
               if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
               if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
               {
               if ( StringLen(BasicPairsLeft[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
                  if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;                  
                  BasicPairsLeft[j].Value=Half1;
                  break;
                  }
               }            
            }
            
         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsLeft[j].Value == Half2 )
               {
               if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
               if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
               {
               if (  StringLen(BasicPairsLeft[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
                  if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;                  
                  BasicPairsLeft[j].Value=Half2;
                  break;
                  }
               }            
            }            
                  
         ReadStartIterator=i+1;
         quantityiterator++;
         }
      }
   /// end of left-side balance calculation
      
   //// Calculate balance values for the right side
   quantityiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(CheckedPair.RightSide); i++ )// extract base currencies from the right side of the equation
      {
      Divider=StringSubstr(CheckedPair.RightSide,i,1);

      if ( Divider == "^"|| i == StringLen(CheckedPair.RightSide) - 1 )
         {
         SubPair=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,6);
         SubSide=StringSubstr(CheckedPair.RightSideStructure,quantityiterator,1);
         Half1=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,3);
         Half2=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE+3,3);         

         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsRight[j].Value == Half1 )
               {
               if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
               if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
               {
               if (  StringLen(BasicPairsRight[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
                  if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;                  
                  BasicPairsRight[j].Value=Half1;
                  break;
                  }
               }            
            }
            
         bNew=true;
         for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
            {
            if ( BasicPairsRight[j].Value == Half2 )
               {
               if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
               if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;
               bNew = false;
               break;
               }
            }
         if ( bNew )
            {
            for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
               {
               if (  StringLen(BasicPairsRight[j].Value) == 0 )
                  {
                  if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
                  if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;                  
                  BasicPairsRight[j].Value=Half2;
                  break;
                  }
               }            
            }            
                  
         ReadStartIterator=i+1;
         quantityiterator++;
         }
      }
   /// end of right-side balance calculation
 
   /// calculate the number of lower and upper currencies based on the received data from the previous block
   int LeftUpTotal=0;// the number of upper elements in the left part
   int LeftDownTotal=0;// the number of lower elements in the left part
   int RightUpTotal=0;// the number of upper elements in the right part
   int RightDownTotal=0;// the number of lower elements in the right part
   
   
   string LastUpLeft;
   string LastDownLeft;
   string LastUpRight;
   string LastDownRight;   
   for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )
      {
      if ( BasicPairsLeft[i].Quantity > 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[i].Quantity;
      if ( BasicPairsLeft[i].Quantity < 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[i].Quantity;
      }
   for ( int i=0; i<ArraySize(BasicPairsRight); i++ )
      {
      if ( BasicPairsRight[i].Quantity > 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightUpTotal+=BasicPairsRight[i].Quantity;
      if ( BasicPairsRight[i].Quantity < 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightDownTotal-=BasicPairsRight[i].Quantity;
      }      
   ///
   /// check if both sides are equal
   if ( LeftUpTotal == 1 && LeftDownTotal == 1 && RightUpTotal == 1 && RightDownTotal == 1 )// there must be one pair in the upper and in the lower part of both sides of the equality, otherwise the formula is invalid
      {
      for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )
         {
         if ( BasicPairsLeft[i].Quantity == 1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastUpLeft=BasicPairsLeft[i].Value;
         if ( BasicPairsLeft[i].Quantity == -1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastDownLeft=BasicPairsLeft[i].Value;
         }
      for ( int i=0; i<ArraySize(BasicPairsRight); i++ )
         {
         if ( BasicPairsRight[i].Quantity == 1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastUpRight=BasicPairsRight[i].Value;
         if ( BasicPairsRight[i].Quantity == -1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastDownRight=BasicPairsRight[i].Value;
         }      
      }
   else return false;
   if ( (LastUpLeft == LastUpRight && LastDownLeft == LastDownRight) || (LastUpLeft == LastDownRight && LastDownLeft == LastUpRight) )
      {
      if ( LastUpLeft == LastDownRight && LastDownLeft == LastUpRight )// If the formula is cross-equivalent, then invert the structure of the right part of the equation (it is the same as raising to the power of -1)
         {
         string NewStructure;// the new structure that will be built from the previous one
         for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ )
            {
            if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d";
            if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u";
            }
         CheckedPair.RightSideStructure=NewStructure;
         }      
      }
   else return false;// if the resulting fractions on both sides are not equivalent, then the formula is invalid
   if ( LastUpLeft == LastDownLeft ) return false;// if result in one, then the formula is invalid

  /// Now it is necessary to write all the above into a corrected and more convenient structure
   string TempResult=CorrectedResultInstrument(LastUpLeft+LastDownLeft,r.IsResultInstrument);
   if ( r.IsResultInstrument && LastUpLeft+LastDownLeft != TempResult ) 
      {
      string NewStructure="";// the new structure that will be built from the previous one
      for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ )
         {
         if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d";
         if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u";
         }
      CheckedPair.RightSideStructure=NewStructure;
      NewStructure="";// the new structure that will be built from the previous one
      for ( int i=0; i<StringLen(CheckedPair.LeftSideStructure); i++ )
         {
         if ( CheckedPair.LeftSideStructure[i] == 'u' ) NewStructure+="d";
         if ( CheckedPair.LeftSideStructure[i] == 'd' ) NewStructure+="u";
         }
      CheckedPair.LeftSideStructure=NewStructure;      
        
      r.ResultInstrument=LastDownLeft+LastUpLeft;
      r.UpPair=LastDownLeft;
      r.DownPair=LastUpLeft;      
      }
   else
      {
      r.ResultInstrument=LastUpLeft+LastDownLeft;
      r.UpPair=LastUpLeft;
      r.DownPair=LastDownLeft;
      }

   r.LeftSide=CheckedPair.LeftSide;
   r.RightSide=CheckedPair.RightSide;
   r.LeftSideStructure=CheckedPair.LeftSideStructure;
   r.RightSideStructure=CheckedPair.RightSideStructure;
   ///   
    
   /// if code has reached this point, it is considered that we have found the formula meeting the criteria, and the next step is normalization
      
   return true;
   }

绿色高亮显示的函数可用来判定品种列表是否包含已简化公式的品种。 结果也许是公式已被简化，例如，不是 “USDJPY”，而是 “JPYUSD”。 这个品种显然不存在，即使它能够被创建。 但我们的任务是修改公式，令其产生正确的交易金融产品。 在这种情况下，公式的两部分都应计算 -1 次幂，这相当于将公式的结构颠倒（将 “d” 改为 “u”，反之亦然）。 若在市场观察窗口中没有该品种，则保持原样：

string CorrectedResultInstrument(string instrument, bool &bResult)// if any equivalent symbol corresponds to the generated formula, return this symbol (or leave as is)
   {   
   string Half1="";
   string Half2="";   
   string Half1input=StringSubstr(instrument,0,3);//input upper currency
   string Half2input=StringSubstr(instrument,3,3);//input lower currency
   bResult=false;
   for ( int j=0; j<ArraySize(Pairs); j++ )
      {
      Half1=StringSubstr(Pairs[j].Name,PrefixE,3);
      Half2=StringSubstr(Pairs[j].Name,PrefixE+3,3);
      if ( (Half1==Half1input && Half2==Half2input) || (Half1==Half2input && Half2==Half1input) )// direct match or crossed match
         {
         bResult=true;
         return Pairs[j].Name;
         }
      }
   
   return instrument;
   }

我准备了以下结构来存储已由过滤器筛选的公式。 该结构有一些来自以前的字段和一些新的字段：

struct EquationCorrected // corrected structure of the basic formula
   {
   string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign
   string LeftSideStructure;// structure of the left side of the formula
   string RightSide;// currency pairs participating in the right side of the formula
   string RightSideStructure;// structure of the right side of the formula
   
   string ResultInstrument;// the resulting instrument to which both parts of the formula come after transformation
   bool IsResultInstrument;// has the suitable equivalent symbol been found
   string UpPair;// the upper currency of the resulting instrument
   string DownPair;// the lower currency of the resulting instrument
   };

公式常规化

此过程是结果筛选的下一步。 它由以下顺序操作组成，其按顺序一个接一个：

1. 依据来自等式两边获得的结果品种，从列表中为等式两边选择一个起始货币对。
2. 两个货币对，根据它们在等式中的比重，必须在分数提名者中提供基准货币
3. 如果找到这样的货币对，并且分数的较低货币不包含结果金融产品的主要货币，则要更进一步
4. 我们深入前进，下一个货币对的上位货币补偿前一个货币对的下位货币
5. 重复这些步骤，直到找到所需的结果货币对
6. 一旦找到结果货币对，公式中所有未用成分都会被舍弃（因为它们的乘积是一）
7. 与此过程并行，“手数因子”按货币对顺序计算（它们显示您需要为特定货币对开仓的手数，来确保我们的金融产品）
8. 结果被写入一个新变量当中，其将在下一个分析阶段使用。

函数代码如下：

bool bNormalized(EquationCorrected &d,EquationNormalized &v)// formula normalization attempt (the normalized formula is returned in "v" )
   {
   double PreviousContract;// previous contract
   bool bWasPairs;// if any pairs have been found
   double BaseContract;// contract of the pair to which the equation is reduced
   double PreviousLotK=0.0;// previous LotK
   double LotK;// current LotK
   string PreviousSubSide;// in numerator or denominator (previous factor)
   string PreviousPair;// previous pair
   string PreviousHalf1;// upper currency of the previous pair
   string PreviousHalf2;// lower currency of the previous pair
   string SubPair;// the full name of the currency pair
   string Half1;// the first currency of the pair
   string Half2;// the second currency of the pair
   string SubSide;// the currency pair in the numerator or denominator
   string Divider;// separator
   int ReadStartIterator=0;// reading start index
   int quantityiterator=0;// quantity
   int tryiterator=0;// the number of balancing attempts
   int quantityleft=0;// the number of pairs on the left after normalization
   int quantityright=0;//the number of pairs on the right after normalization
   bool bNew;
   BasicValue b0;
   
   for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs 
      {
      BasicPairsLeft[i].Value = "";
      BasicPairsLeft[i].Quantity = 0;
      }
   for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs
      {
      BasicPairsRight[i].Value = "";
      BasicPairsRight[i].Quantity = 0;
      }
      
   if ( d.IsResultInstrument ) BaseContract=SymbolInfoDouble(d.ResultInstrument, SYMBOL_TRADE_CONTRACT_SIZE);// define the contract of the equivalent pair based on the instrument
   else BaseContract=100000.0;
      
   //// Calculate the number of pairs for the left side
   tryiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation
      {
      Divider=StringSubstr(d.LeftSide,i,1);
      if ( Divider == "^" )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }
         
      if ( i == StringLen(d.LeftSide) - 1 )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }         
      }
   /// end of quantity calculation for the left part
      
   ArrayResize(v.PairLeft,tryiterator);
   /// calculate the lot coefficients for the left side
   
   bool bBalanced=false;// is the formula balanced
   bool bUsed[];
   ArrayResize(bUsed,tryiterator);
   ArrayFill(bUsed,0,tryiterator,false);
   int balancediterator=0;
   PreviousHalf1="";
   PreviousHalf2="";
   PreviousLotK=0.0;
   PreviousSubSide="";
   PreviousPair="";
   PreviousContract=0.0;
   bWasPairs=false;// have there been pairs
   for ( int k=0; k<tryiterator; k++ )// try to normalize the left side
      {
      if( !bBalanced )
         {
         quantityiterator=0;
         ReadStartIterator=0;
         for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation
            {
            Divider=StringSubstr(d.LeftSide,i,1);
            if ( Divider == "^" || i == StringLen(d.LeftSide) - 1 )
               {
               SubPair=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,6);
               SubSide=StringSubstr(d.LeftSideStructure,quantityiterator,1);
               Half1=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,3);
               Half2=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE+3,3);         
            
               if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list
               || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator
               || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator
                  {// find the entry point(pair) of the chain
                  if( PreviousHalf1 == "" )// define the lot coefficient of the first pair
                     {
                     if ( SubSide == "u" )
                        {
                        LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start)
                        v.PairLeft[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }
                     if ( SubSide == "d" )
                        {
                        double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                        if ( Pt == 0.0 ) return false; 
                        LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start)
                        v.PairLeft[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }                     
                     }
                  else
                     {
                     if( PreviousSubSide == "u" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false; 
                           LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 1 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false; 
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;                           
                           LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 2 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }
                     if( PreviousSubSide == "d" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           if ( PreviousContract <= 0.0 ) return false;
                           LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 3 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;
                           LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 4 )
                           v.PairLeft[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }                  
                     }
                                   
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsLeft[j].Value == Half1 )
                        {
                        if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
                        if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                        {
                        if ( StringLen(BasicPairsLeft[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++;
                           if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--;                  
                           BasicPairsLeft[j].Value=Half1;
                           break;
                           }
                        }            
                     }
            
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsLeft[j].Value == Half2 )
                        {
                        if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
                        if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                        {
                        if (  StringLen(BasicPairsLeft[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--;
                           if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++;                  
                           BasicPairsLeft[j].Value=Half2;
                           break;
                           }
                        }            
                     }
                  
                  v.PairLeft[balancediterator].Name=SubPair;
                  v.PairLeft[balancediterator].Side=SubSide;
                  v.PairLeft[balancediterator].ContractSize=SymbolInfoDouble(v.PairLeft[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE);
               

                  balancediterator++;                  
                  PreviousHalf1=Half1;
                  PreviousHalf2=Half2;
                  PreviousSubSide=SubSide;
                  PreviousPair=SubPair;
                  
                  quantityleft++;
                  if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted
                     {
                     bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                  if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted
                     {
                     bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                  
                  int LeftUpTotal=0;// the number of upper elements in the left part
                  int LeftDownTotal=0;// the number of lower elements in the left part
                  string LastUpLeft;
                  string LastDownLeft;
                  for ( int z=0; z<ArraySize(BasicPairsLeft); z++ )
                     {
                     if ( BasicPairsLeft[z].Quantity > 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[z].Quantity;
                     if ( BasicPairsLeft[z].Quantity < 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[z].Quantity;
                     }
                  if ( bWasPairs && LeftUpTotal == 0 && LeftDownTotal == 0 ) return false;                                           
                  }

               ReadStartIterator=i+1;
               bUsed[quantityiterator]=true;
               quantityiterator++;
               }
            }
         }
         else break;
      }
   /// end of coefficient calculation for the left part
     
   if ( !bBalanced ) return false;// if the left side is not balanced, then there is no point in balancing the right side
     
   //// Calculate the number of pairs for the right side
   tryiterator=0;
   ReadStartIterator=0;
   for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation
      {
      Divider=StringSubstr(d.RightSide,i,1);
      if ( Divider == "^" )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }
         
      if ( i == StringLen(d.RightSide) - 1 )
         {
         ReadStartIterator=i+1;
         tryiterator++;
         }         
      }   
   ArrayResize(v.PairRight,tryiterator);
   /// end of calculation of the number of pairs for the right side
     
   bBalanced=false;// is the formula balanced
   ArrayResize(bUsed,tryiterator);
   ArrayFill(bUsed,0,tryiterator,false);
   balancediterator=0;
   PreviousHalf1="";
   PreviousHalf2="";
   PreviousLotK=0.0;
   PreviousSubSide="";
   PreviousPair="";
   PreviousContract=0.0;
   bWasPairs=false;
   for ( int k=0; k<tryiterator; k++ )// try to normalize the right side
      {
      if ( !bBalanced )
         {
         quantityiterator=0;
         ReadStartIterator=0;
         for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation
            {
            Divider=StringSubstr(d.RightSide,i,1);
            if ( Divider == "^" || i == StringLen(d.RightSide) - 1 )
               {
               SubPair=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,6);
               SubSide=StringSubstr(d.RightSideStructure,quantityiterator,1);
               Half1=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,3);
               Half2=StringSubstr(d.RightSide,ReadStartIterator+PrefixE+3,3);         
            
               if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list
               || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator
               || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator
                  {// find the entry point(pair) of the chain
                  if( PreviousHalf1 == "" )// define the lot coefficient of the first pair
                     {
                     if ( SubSide == "u" )
                        {
                        LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start)
                        v.PairRight[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }
                     if ( SubSide == "d" )
                        {
                        double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                        if ( Pt == 0.0 ) return false; 
                        LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start)
                        v.PairRight[balancediterator].LotK=LotK;
                        PreviousLotK=LotK;
                        bWasPairs=true;
                        PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                        }                     
                     }
                  else
                     {
                     if( PreviousSubSide == "u" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;                            
                           LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (1)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false; 
                           if ( Pp == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false;                            
                           LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (2)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }
                     if( PreviousSubSide == "d" )// define the lot coefficient of further pairs
                        {
                        if ( SubSide == "u" )
                           {
                           if ( PreviousContract <= 0.0 ) return false;
                           LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (3)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }
                        if ( SubSide == "d" )
                           {
                           double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID);
                           if ( Pt == 0.0 ) return false;
                           if ( PreviousContract <= 0.0 ) return false; 
                           LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (4)
                           v.PairRight[balancediterator].LotK=LotK;
                           PreviousLotK=LotK;
                           PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);
                           }                     
                        }                  
                     }                
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsRight[j].Value == Half1 )
                        {
                        if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
                        if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it
                        {
                        if ( StringLen(BasicPairsLeft[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsRight[j].Quantity++;
                           if ( SubSide == "d" ) BasicPairsRight[j].Quantity--;                  
                           BasicPairsRight[j].Value=Half1;
                           break;
                           }
                        }            
                     }
            
                  bNew=true;
                  for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
                     {
                     if ( BasicPairsRight[j].Value == Half2 )
                        {
                        if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
                        if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;
                        bNew = false;
                        break;
                        }
                     }
                  if ( bNew )
                     {
                     for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it
                        {
                        if (  StringLen(BasicPairsRight[j].Value) == 0 )
                           {
                           if ( SubSide == "u" ) BasicPairsRight[j].Quantity--;
                           if ( SubSide == "d" ) BasicPairsRight[j].Quantity++;                  
                           BasicPairsRight[j].Value=Half2;
                           break;
                           }
                        }            
                     }
                  
                  v.PairRight[balancediterator].Name=SubPair;
                  v.PairRight[balancediterator].Side=SubSide;
                  v.PairRight[balancediterator].ContractSize=SymbolInfoDouble(v.PairRight[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE);


                  balancediterator++;                  
                  PreviousHalf1=Half1;
                  PreviousHalf2=Half2;
                  PreviousSubSide=SubSide;
                  PreviousPair=SubPair;
               
                  quantityright++;
                  if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted
                     {
                     bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                  if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted
                     {
                     bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula
                     break;// since the formula is balanced, we don't need the rest
                     }
                     
                  int RightUpTotal=0;// the number of upper elements in the right part
                  int RightDownTotal=0;// the number of lower elements in the right part
                  string LastUpRight;
                  string LastDownRight; 
                    
                  for ( int z=0; z<ArraySize(BasicPairsRight); z++ )
                     {
                     if ( BasicPairsRight[z].Quantity > 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightUpTotal+=BasicPairsRight[z].Quantity;
                     if ( BasicPairsRight[z].Quantity < 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightDownTotal-=BasicPairsRight[z].Quantity;
                     }
                  if ( bWasPairs && RightUpTotal == 0 && RightDownTotal == 0 ) return false;                                       
                  }

               ReadStartIterator=i+1;
               bUsed[quantityiterator]=true;
               quantityiterator++;
               }
            }
         }
         else break;
      }     
   
   if ( quantityleft == 1 && quantityright == 1 ) return false;// if the equation has been normalized to only 2 pairs, it is not valid (at least 3 pairs are required)
      
   return bBalanced;
   }

这是一个非常健康和复杂的过程，但在我看来，在这种情况下最好不要产生中间状态，因为这会导致大量的代码重复。 甚至，所有阶段都非常紧凑，并且在逻辑上被划分为多个模块。 这些函数集合为我们提供了绝对相同的结果，其与我们手工转换得到的结果完全相同。 在此，所有这些数学运算都是通过一组复杂但必要的方法来执行的。

我们需要执行特殊分析，来了解所发现公式的盈利能力如何。 不要忘记，每个货币对都可以朝上和朝下双向开仓。 故此，对于每个公式，可以有两个中间回路变体 - 正向和逆向。 最高盈利能力的那个作为最终结果承认。

为了评估盈利能力，我已创建了一个类似于利润因子的指标，它由掉期利率产生的盈利和亏损组成。 如果已有回路的累计正掉期利率大于负值模组，则认为这样的线路有利可图。 在其他情况下，这样的回路是无利可图的 — 换言之，我们的掉期利率因子等高线只有当它大于 1 时才会为正值。

返回的结果被写入一个完全不同的容器之中，所创建容器可用于交易和进一步开发交易逻辑的自洽命令包。 它包含快速轻松地开立整个回路所需的一切：

struct EquationNormalized // the final structure with the formula in normalized form
   {
   Pair PairLeft[];// currency pairs on the left side
   Pair PairRight[];// currency pairs on the right side
   double SwapPlusRelative;// relative equivalent of the positive swap
   double SwapMinusRelative;// relative equivalent of the negative swap
   double SwapFactor;// resulting swap factor
   };

我还添加了两个方法，能够方便地显示有关内容的信息，但它们与本文无关，故我不会在这里提供它们。 您可以在附带的源代码中查看它们。 现在，关于等式每个分量的信息会作为数组元素单独包含。 这令以后操控数据更容易，且无需持续地从字符串中解析它们。 也许，这个解决方案可从最开始就采用，但这会破坏可读性。

掉期利率因子的计算和等式结构的最终调整

这是最后阶段，在其中计算该系统最重要的变量 — 将根据该值比较变体。 拥有最高数值的那个就是最佳的。

void CalculateBestVariation(EquationNormalized &ii)// calculation of the best swap factor of the formula and final structure adjustment if needed
   {
   double SwapMinus=0.0;// total negative swap
   double SwapPlus=0.0;// total positive swap
   double SwapMinusReverse=0.0;// total negative swap
   double SwapPlusReverse=0.0;// total positive swap
   
   double SwapFactor=0.0;// swap factor of the direct pass
   double SwapFactorReverse=0.0;// swap factor of the reverse pass
   
   for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// define the missing parameters for calculating the left side
      {
      for ( int j=0; j<ArraySize(Pairs); j++ )
         {
         if ( Pairs[j].Name == ii.PairLeft[i].Name )
            {
            ii.PairLeft[i].Margin=Pairs[j].Margin;
            ii.PairLeft[i].TickValue=Pairs[j].TickValue;
            ii.PairLeft[i].SwapBuy=Pairs[j].SwapBuy;
            ii.PairLeft[i].SwapSell=Pairs[j].SwapSell;
            break;
            }
         }
      }
      
   for ( int i=0; i<ArraySize(ii.PairRight); i++ )// define the missing parameters for calculating the right side
      {
      for ( int j=0; j<ArraySize(Pairs); j++ )
         {
         if ( Pairs[j].Name == ii.PairRight[i].Name )
            {
            ii.PairRight[i].Margin=Pairs[j].Margin;
            ii.PairRight[i].TickValue=Pairs[j].TickValue;
            ii.PairRight[i].SwapBuy=Pairs[j].SwapBuy;
            ii.PairRight[i].SwapSell=Pairs[j].SwapSell;
            break;
            }
         }
      }      
   
   double TempSwap;
   // calculate all components taking into account a change in the structure
   for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// for left parts
      {
      if ( ii.PairLeft[i].Side == "u" )
         {// for direct trading
         TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      if ( ii.PairLeft[i].Side == "d" )
         {// for direct trading
         TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      }
      
   for ( int i=0; i<ArraySize(ii.PairRight); i++ )// for right parts
      {
      if ( ii.PairRight[i].Side == "d" )
         {// for direct trading
         TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      if ( ii.PairRight[i].Side == "u" )
         {// for direct trading
         TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlus+=TempSwap;
         else SwapMinus-=TempSwap;
         // for reverse trading
         TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i];
         if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap;
         else SwapMinusReverse-=TempSwap;         
         }
      }   
   // calculate the swap factor for the direct pass
   if ( SwapMinus > 0.0 && SwapPlus > 0.0 ) SwapFactor=SwapPlus/SwapMinus;
   if ( SwapMinus == 0.0 && SwapPlus == 0.0 ) SwapFactor=1.0;
   if ( SwapMinus == 0.0 && SwapPlus > 0.0 ) SwapFactor=1000001.0;
   if ( SwapMinus > 0.0 && SwapPlus == 0.0 ) SwapFactor=0.0;
   // calculate the swap factor for the reverse pass
   if ( SwapMinusReverse > 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=SwapPlusReverse/SwapMinusReverse;
   if ( SwapMinusReverse == 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=1.0;
   if ( SwapMinusReverse == 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=1000001.0;
   if ( SwapMinusReverse > 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=0.0;
   // select the best approach and calculate the missing values in the structure
   if ( SwapFactor > SwapFactorReverse )
      {
      ii.SwapPlusRelative=SwapPlus;
      ii.SwapMinusRelative=SwapMinus;
      ii.SwapFactor=SwapFactor;
      }
   else
      {
      ii.SwapPlusRelative=SwapPlusReverse;
      ii.SwapMinusRelative=SwapMinusReverse;
      ii.SwapFactor=SwapFactorReverse;
      bool bSigned;
      for ( int i=0; i<ArraySize(ii.PairRight); i++ )// if it is a reverse pass, then reverse the right structure of the formula
         {
         bSigned=false;
         if ( !bSigned && ii.PairRight[i].Side == "u" ) 
            {
            ii.PairRight[i].Side="d";
            bSigned=true;
            }
         if ( !bSigned && ii.PairRight[i].Side == "d" ) 
            {
            ii.PairRight[i].Side="u";
            bSigned=true;
            }
         }
      bSigned=false;    
      for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// if it is a reverse pass, then reverse the left structure of the formula
         {
         bSigned=false;
         if ( !bSigned && ii.PairLeft[i].Side == "u" ) 
            {
            ii.PairLeft[i].Side="d";
            bSigned=true;
            }
         if ( !bSigned && ii.PairLeft[i].Side == "d" ) 
            {
            ii.PairLeft[i].Side="u";
            bSigned=true;
            }
         }              
      }
      
   bool bSigned;
   for ( int i=0; i<ArraySize(ii.PairRight); i++ )// reverse the right side anyway
      {
      bSigned=false;
      if ( !bSigned && ii.PairRight[i].Side == "u" ) 
         {
         ii.PairRight[i].Side="d";
         bSigned=true;
         }
      if ( !bSigned && ii.PairRight[i].Side == "d" ) 
         {
         ii.PairRight[i].Side="u";
         bSigned=true;
         }
      }
   }

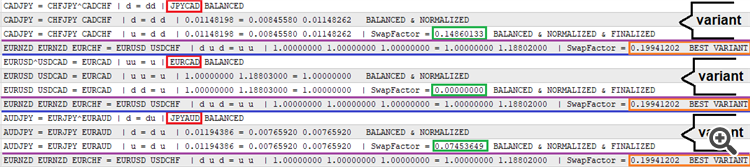
为了启用结果的顺序输出，我实现了仅在找到筛选成功的公式变体时才写入日志。 日志如下：

红色代表生成的品种，等式两边均简化。 下一行展示了含有手数系数的常规化变体。 第三行展示了含有所计算出的掉期利率因子的变体。 第四行是在暴力区间发现的最佳变体，它也由 Comment 函数绘制在图表上。 该原型附在下面，如此您即可测试它。 实际上，它可以作为掉期利率交易的交易助手原型。 至于现在，它的功能还很少，但我会在下一篇文章中尝试扩展它。 该原型有两个版本：分别对应 MetaTrader 4 和 MetaTrader 5。

第一次测试的结论

单就如此复杂的主题很难得出任何结论。 尽管如此，我还是设法了解一些有用的东西，虽然到目前为止我还没有找到大于 1 的掉期利率因子。 这些是我在分析这个原型的操作时得出的第一批结论：

• 对于某些货币对，您可以增加正掉期利率，或减少负掉期利率（由于仓位表现为合成等价物）
• 即使没有找到有利可图的回路，其某个部分始终可用来替代仓位 - 在两个不同的交易账户之间锁定。
• 以这种合成仓位锁定就可剔除使用无掉期利率账户的需求，因为它允许在互逆的两端均拥有正掉期利率。
• 有必要针对最热门的经纪商执行更佳的深入分析，为此需要扩展功能。
• 我希望我能够证明可盈利掉期利率因子是能实现的（到目前为止这只是一个猜测）
• 如若操作得当，掉期利率可提供少量但稳定的利润

结束语

我希望这种方式能引起您的兴趣，并可提供精神食粮。 该方法难予理解，但实际上它实现了一个简单的原理：以相同的交易量开立两笔互逆的持仓。 若仅开立这两笔相逆的持仓总会产生亏损。 没有任何一家经纪商提供一个单向正掉期利率大于逆向负掉期利率模组。 当然，您永远不会在两个方向上找到正掉期利率，因为从数学上它是不可能的。

我不会提供基础数学的细节，因为这是一个非常宽泛的话题。 最好采用这种数学的表现形式。 通过应用所讲述的方法，可以减少由持仓锁定导致的掉期利率亏损。 您还可以尝试在经纪商的掉期利率表中找到一个缝隙，并享受以正利润因子锁定（所有持仓的盈利总掉期利率）— 这就是不依赖价格波动的无风险交易。

我认为掉期利率交易方法真的被低估了，因为正掉期利率提供了潜在的利润。 所讲述的方法只是掉期利率交易方法的可能变体之一，但我喜欢这个任务，我在下一篇文章中将尝试继续开发新思路、创新代码、并创建新的附加功能。 我还将讲述一些有关利润预测和交易功能的思路。