
스왑(1부): 잠금 및 합성 포지션
목차
소개
저는 이 글의 주제에 대해 오랫동안 생각해 봤지만 자세한 조사를 할 시간이 없었습니다. 스왑에 대한 주제는 웹에 꽤 널리 퍼져 있으며 주로 모든 핍을 계산하는 트레이딩 전문가들 사이에서는 실제로 가장 좋은 트레이딩 방식입니다. 이 글에서는 스왑을 유용하게 사용하는 방법에 대해 알아볼 것입니다. 그러면 여러분은 스왑을 항상 고려해야 한다는 것을 알게 될 것입니다. 또한 이 기사에는 스왑 거래 방식을 현대화 하는 방법에 대한 매우 복잡하지만 흥미로운 아이디어가 소개되어 있습니다. 이러한 방법은 (적절히 준비된 경우) 하나의 계좌 내에서 사용하거나 두 개의 계좌를 사용하여 하는 고전적 잠금을 통한 수익 향상 도구로 사용할 수 있습니다.
스왑이란
스왑의 개념과 이론에 대해서는 설명하지 않겠습니다. 저는 스왑의 실제 적용에만 관심이 있습니다. 가장 중요한 질문은 스왑을 통해 수익을 창출할 수 있는지 여부입니다. 트레이더의 관점에서 스왑은 이익 또는 손실입니다. 게다가 많은 트레이더들은 장중 거래를 고수하기 때문에 스왑을 무시합니다. 또 다른 사람들은 거래에 거의 영향을 미치지 않을 정도로 중요하지 않다고 생각하여 주의를 기울이지 않으려고 합니다. 실제로 스프레드의 거의 절반이 스왑에 숨겨져 있습니다. 이 스프레드는 매수 또는 매도 시점이 아니라 서버에서 날짜가 변경되는 시점을 기준으로 합니다.
스왑은 오픈 포지션 볼륨을 기준으로 청구됩니다. 이는 다음과 같은 순간에 발생합니다:
- 월요일~화요일
- 화요일~수요일
- 수요일부터 목요일까지(거의 모든 브로커가 이 날 밤에 트리플 스왑을 청구합니다)
- 목요일~금요일
일반적으로 스왑 값은 거래 상품 명세서에 포인트 또는 백분율로 표시되어 있습니다. 다른 계산 방법도 있을 수 있지만 저는 그 중 두 가지 방법만 이해할 수 있었습니다. 스왑에 대한 체계적인 정보는 거의 없습니다. 하지만 질문을 잘 살펴보면 효율적인 스왑 기반 전략을 찾을 수있을 것입니다. 스왑 기반의 전략은 최소한의 수익률을 창출하지만 수익이 절대적으로 보장된다는 큰 장점이 있습니다. 이 접근 방식의 가장 큰 어려움은 가장 인기있는 브로커는 포지티브 스왑인 상품이 거의 없기 때문에 이 아이디어로 돈을 벌기가 정말 어렵다는 사실입니다. 잠재적인 수익 가능성조차 극히 낮습니다. 그래도 증거금을 완전히 잃는 것보다는 낫습니다. 여러분이 다른 트레이딩 시스템을 사용 중이라면 손실 가능성이 높습니다.
외환 거래에서 결론은 포지티브 스왑을 제외하고는 수익을 보장할 수 있는 것은 없다는 것입니다. 물론 수익을 창출할 수 있는 일부의 시스템도 있습니다. 그러나 이를 사용할 때 우리는 모든 거래 작업에 대해 브로커에게 돈을 지불하는 데 동의합니다. 그리고 가격이 올바른 방향으로 진행되기를 바랍니다. 포지티브 스왑은 그 반대의 과정입니다. 저는 다음 문장을 포지티브 스왑 방향으로 거래하는 것의 지표로 보고 있습니다:
- 포지티브 스왑은 오픈 포지션을 향한 부분적인 가격 변동(매일 수익)과 동일합니다.
- 일정 시간이 지나면 스왑을 통해 스프레드 및 수수료 손실을 보전할 수 있으며 시간이 지나면 스왑을 통해 수익이 추가됩니다.
- 스왑이 작동하려면 포지션을 가능한 한 오래 유지해야 합니다. 그러고 나서 이 포지션의 수익 계수가 최대가 됩니다.
- 만약 이를 철저하게 개발하면 수익은 절대적으로 예측 가능하고 보장됩니다.
물론 이 접근법의 가장 큰 단점은 증거금의 규모에 의존한다는 것이지만 외환 거래에서 이만큼 자신 있게 수익을 보장할 수 있는 개념은 없습니다. 그로나 이 부분은 진입한 포지션의 규모나 리스크를 줄임으로써 줄일 수 있습니다(사실상 둘이 동일). 위험은 포지션 거래량과 증거금의 비율입니다: 포지션 볼륨이 증가하면 가격이 손실의 방향으로 갈 위험이 커지고 스왑으로 인한 수익이 스프레드와 수수료 손실을 보상할 때까지 기다리기에는 증거금이 충분하지 않을 수 있습니다. 가능한 모든 부정적인 것들의 영향을 최소화하기 위해 잠금 메커니즘이 발명되었습니다.
두 개의 트레이딩 계좌를 이용한 잠금
이 스왑 거래 방식은 트레이더들 사이에서 가장 인기 있는 거래 방식입니다. 이 전략을 실행하려면 동일한 통화쌍 또는 기타의 자산에 대해 서로 다른 스왑을 사용하는 두 개의 계좌가 필요합니다. 같은 계좌에서 서로 반대되는 포지션을 두 개 개설하는 것은 의미가 없으며 이는 단순히 증거금을 잃는 것과 마찬가지입니다. 심볼이 포지티브 스왑을 가지고 있더라도 반대 방향으로 거래하면 이 스왑은 마이너스가 됩니다. 다음 다이어그램은 이 방법의 개념을 반영합니다:
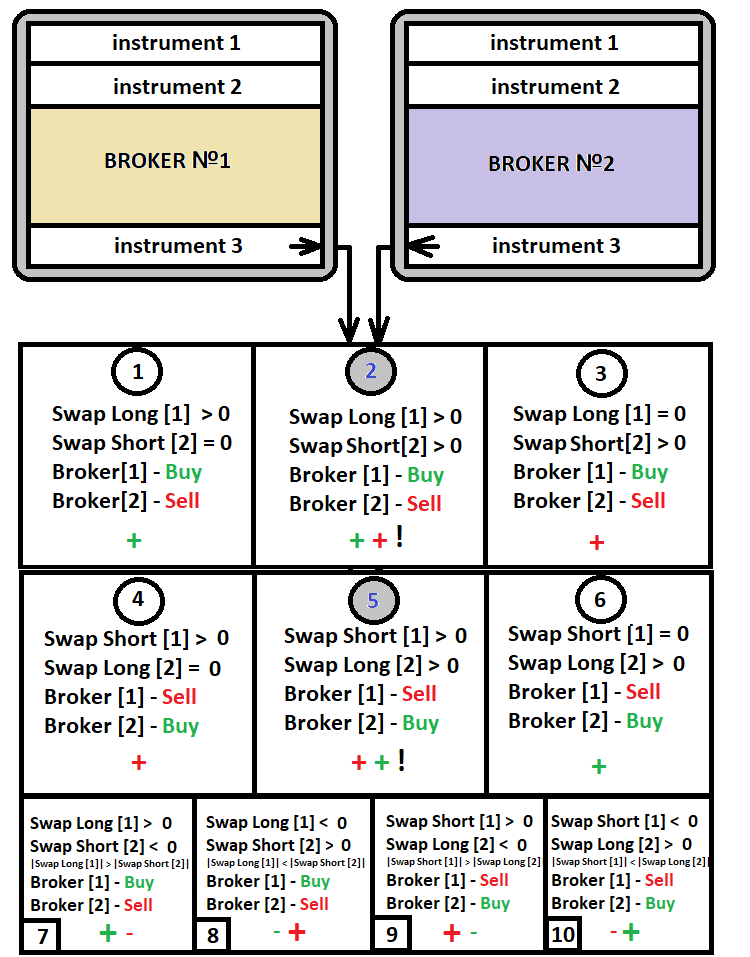
다이어그램에서 볼 수 있듯이 우리가 스왑을 거래하려는 특정한 상품의 거래 시나리오는 10가지뿐이며 이 중 6가지가 활발히 사용되고 있습니다. 마지막 네 가지 옵션은 조건 "1-6"과 일치하는 통화쌍을 찾을 수 없는 경우 여기서 스왑 중 하나가 마이너스이기 때문에 최후의 수단으로 선택될 수 있습니다. 마이너스 스왑보다 큰 포지티브 스왑을 통해 수익을 얻을 수 있습니다. 여러 브로커와 스왑 테이블을 분석하면 위에 언급된 모든 사례를 찾을 수 있습니다. 하지만 이 전략에 가장 적합한 옵션은 '2'와 '5'입니다. 이러한 옵션은 양쪽 끝에 포지티브 스왑이 있습니다. 따라서 수익은 두 브로커 모두에서 발생합니다. 또한 계좌 간에 자금을 자주 옮길 필요가 없습니다.
이 전략의 가장 큰 단점은 반대의 포지션에 진입할 때 한 브로커에서는 손실이 발생하고 다른 브로커에서는 이익이 발생하기 때문에 계좌 간 자금 이동이 필요하다는 것입니다. 그러나 기존 증거금과 관련하여 거래량을 정확하게 계산하면 자금을 너무 자주 이동할 필요가 없습니다. 그러나 한 가지 확실한 이점이 있습니다. 어떤 경우에도 수익이 발생하고 이 수익의 정확한 규모를 예측할 수 있다는 점입니다. 많은 사용자가 이 루틴을 피하고 어떻게든 하나의 계정 내에서 이러한 조작을 수행하는 것을 선호합니다(불가능하지만). 스왑 거래는 한 계좌 내에서 거래를 하는 것이 아니지만 고전적인 스왑 거래 방법의 수익을 높이는 한 가지 방법이 있습니다. 이 방법의 주요 기능에 대해 설명하겠습니다.
환율이란
모든 로직이 구축되는 기초부터 시작하겠습니다. 이를 기반으로 수학 방정식이 만들어 질 수 있습니다 예를 들어 EURUSD, USDJPY, EURJPY를 생각해 보십시오. 이 세 가지 쌍은 모두 서로 연관되어 있습니다. 관계를 이해하기 위해 이러한 심볼들을 약간 다른 형태로 표현해 보겠습니다:
- 1/P = EUR/USD
- 1/P = USD/JPY
- 1/P = EUR/JPY
- P는 선택한 통화의 비율입니다.
모든 거래 상품에는 우리가 취득하는 통화(또는 이에 상응하는 자산)와 그 대가로 제공하는 다른 통화가 있습니다. 예를 들어 첫 번째 비율(EURUSD 쌍)을 선택하면 1랏 매수 포지션을 개시할 때 여러분은 기본 통화 100,000유닛을 획득하게 됩니다. 외환 거래 규칙은 다음과 같습니다: 1랏은 항상 기본 통화 100,000단위와 동일합니다. 이 쌍의 기본 통화는 EUR이므로 USD로 EUR를 매수합니다. 이 경우 환율 "P"는 1유로에 몇 개의 USD 단위가 포함되어 있는지를 의미합니다. 이는 다른 모든 심볼에도 동일하게 적용됩니다. 분자에 기준 통화가 포함되고 분모는 "주요 통화"가 됩니다(이 명칭에 동의하지 않는 경우 아래에 의견을 추가해 주세요). 기본 통화 금액은 가격에 EUR 값을 곱하여 간단히 계산됩니다:
- 1/P = EUR/USD ---> USD/P= EUR ---> USD = P*ER
- EUR = 랏*100000
매도 포지션에 진입하면 통화의 위치가 바뀝니다. 기본 통화가 기축 통화로 작동하기 시작하고 기축 통화가 기본 통화가 됩니다. 즉 USD를 EUR로 구매하지만 두 통화의 금액은 EUR를 기준으로 동일한 방식으로 계산됩니다. 그렇지 않으면 많은 혼란이 있을 수 있기 때문에 이것은 맞습니다. 다른 통화도 계산은 동일합니다. 따라서 추가 계산에서 베이스 통화는 기호 "+"를 사용하고 메인 통화는 기호 "-"를 사용하겠습니다. 결과적으로 모든 거래에는 우리가 무엇을 그리고 무엇을 위해 구매하는지를 나타내는 두 개의 해당 숫자 세트가 있습니다. 이에 대한 또 다른 해석은 항상 상품의 역할을 하는 통화와 통화의 역할을 하며 상품을 구매하기 위해 지불하는 또 다른 통화가 존재한다는 것입니다.
여러 상품에 대해 여러 포지션을 개설하면 주요 통화와 추가 통화가 더 많아지므로 일종의 합성 포지션이 됩니다. 스왑을 사용하는 관점에서 볼 때 이러한 합성 포지션은 전혀 쓸모가 없습니다. 그러나 우리는 매우 유용한 합성 포지션을 만들 수 있습니다. 잠시 후에 보여드리겠습니다. 두 가지 통화로 표시되는 볼륨의 계산을 결정했습니다. 이를 바탕으로 우리는 간단한 포지션과 비슷한 복잡한 합성 포지션을 만들 수 있다는 결론을 내릴 수 있습니다:
- EUR/JPY = EUR/USD * USD/JPY - 두 가지 파생상품으로 구성된 환율
실제로는 다음과 같은 여러 통화로 구성된 이러한 비율은 무한히 많습니다:
- EUR - 유럽 연합 유로
- USD - 미국 달러
- JPY - 일본 엔
- GBP - 영국 파운드
- CHF - 스위스 프랑
- CAD - 캐나다 달러
- NZD - 뉴질랜드 달러
- AUD - 호주 달러
- CNY - 중국 위안
- SGD - 싱가포르 달러
- NOK - 노르웨이 크로네
- SEK - 스웨덴 크로나
이것은 전체 통화 목록이 아닙니다. 우리가 알아야 할 것은 이 목록에 있는 모든 통화로 차익 거래 상품을 구성할 수 있다는 것입니다. 이러한 상품 중 일부는 브로커가 제공하는 반면 다른 상품은 다른 상품의 포지션을 조합하여 얻을 수 있습니다. 대표적인 예로 EURJPY 쌍을 들 수 있습니다. 이것은 파생상품 환율을 구성하는 가장 간단한 예시일 뿐이지만 우리는 이러한 아이디어를 바탕으로 모든 포지션이 다른 상품의 포지션의 집합으로 표시될 수 있다는 결론을 내릴 수 있습니다. 위의 내용을 보면 우리는 다음을 알 수 있습니다:
- Value1은 절대값으로 표현되는 베이스 심볼 통화입니다.
- Value2는 절대값으로 표현되는 추가 심볼 통화입니다.
- A는 포지션의 베이스 통화의 랏 볼륨입니다.
- B는 포지션의 메인 통화의 랏 볼륨입니다.
- 계약은 매수 또는 매도된 통화량을 절대값으로 표시한 금액입니다(1랏에 해당).
- A = 1/P = Value1/Value2 - 모든 거래 상품(종합시세 창에 표시되지 않는 상품 포함)의 방정식입니다.
- Value1 = Contract*A
- Value2 = Contract*B
나중에 랏을 계산하려면 이 비율이 필요합니다. 지금은 그저 기억해 두세요. 이 비율은 매수 또는 매도되는 통화의 수의 비율을 나타냅니다. 이를 기반으로 더 발전한 코드 로직을 구축할 수 있습니다.
합성 포지션을 사용한 잠금
이 글에서 다루는 합성 포지션은 여러 다른 포지션으로 구성될 수 있는 포지션이며 이러한 다른 포지션은 반드시 다른 상품으로 구성해야 합니다. 이 포지션은 모든 상품에 대해 하나의 진입한 포지션과 동일해야 합니다. 복잡해 보이시나요? 사실 이 모든 것은 매우 간단합니다. 이러한 포지션은 다음을 위해 필요할 수 있습니다:
- 모의 트레이딩 상품에서 원래 포지션 잠그기
- 완전히 다른 스왑 비율로 포지션과 동일한 포지션을 생성해 보세요.
- 기타 목적
이 방법의 일반적인 체계는 다음과 같습니다:
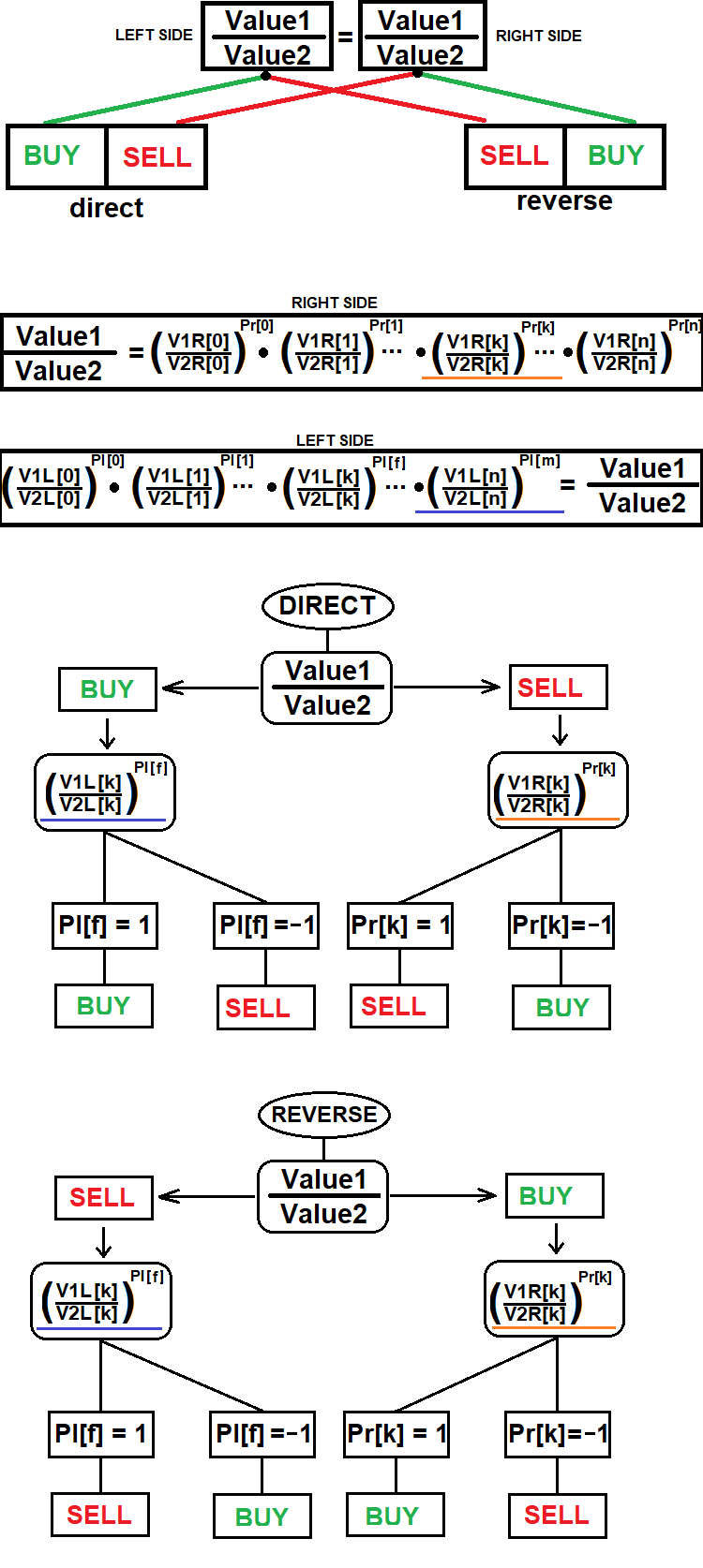
이 계획조차도 합성 포지션을 개설하는 방법에 대한 전체 데이터를 다루지는 않습니다. 이 다이어그램은 선택한 브로커에서 사용 가능한 상품 중 하나로 반드시 표시되어야 하는 합성 포지션의 특정 구성 요소에 대한 거래 방향을 결정하는 방법만 보여줍니다.
이제 우리는 이러한 포지션의 거래량을 계산하는 방법을 결정해야 합니다. 논리적으로 볼륨은 선택한 방정식의 변환이 줄어든 결과 상품의 포지션이 1랏과 같아야 한다는 점을 고려하여 계산해야 합니다. 볼륨 계산에는 다음의 값들이 필요합니다:
- ContractB - 방정식이 축소되는 쌍의 계약 크기(대부분의 경우 기본 통화의 100,000 단위와 같음)
- Contract[1] - 여러분이 랏을 결정하려는 쌍의 계약 크기
- A[1] - 이전 밸런스된 페어(또는 체인 내 첫 번째 페어)의 랏으로 표시된 베이스 통화 금액
- B[1] - 이전 밸런스된 쌍(또는 체인 내 첫 번째)의 랏 단위로 표시된 메인 통화 금액입니다.
- A[2] -현재 밸런스된 쌍의 로트 단위로 표시된 베이스 통화 금액입니다.
- B[2] -현재 밸런스된 쌍의 로트 단위로 표시된 메인 통화 금액입니다.
- C[1] - 이전 밸런스된 쌍(또는 체인 내 첫 번째 페어)의 컨트랙트 크기입니다.
- C[2] - 밸런되는 중인 현재 쌍의 계약 크기
브로커가 조합의 결과 상품을 제공하지 않을 수 있으므로 "ContractB"를 항상 확인할 수 있는 것은 아니라는 점에 유의하시기 바랍니다. 이 경우 계약은 예를 들어 기본 상수 "100000"과 같이 임의로 설정할 수 있습니다.
먼저 원하는 포지션에서 결과 상품의 베이스 통화를 포함하는 체인의 첫 번째 쌍이 결정됩니다. 그런 다음 다른 쌍이 검색되고 이것이 결과 등가물에 포함되지 않은 추가 통화를 보상합니다. 메인 통화가 현재 쌍에서 올바른 위치에 있으면 밸런싱이 끝납니다. 이 작업을 수행하는 방법을 보여드리기 위해 다이어그램을 만들었습니다:
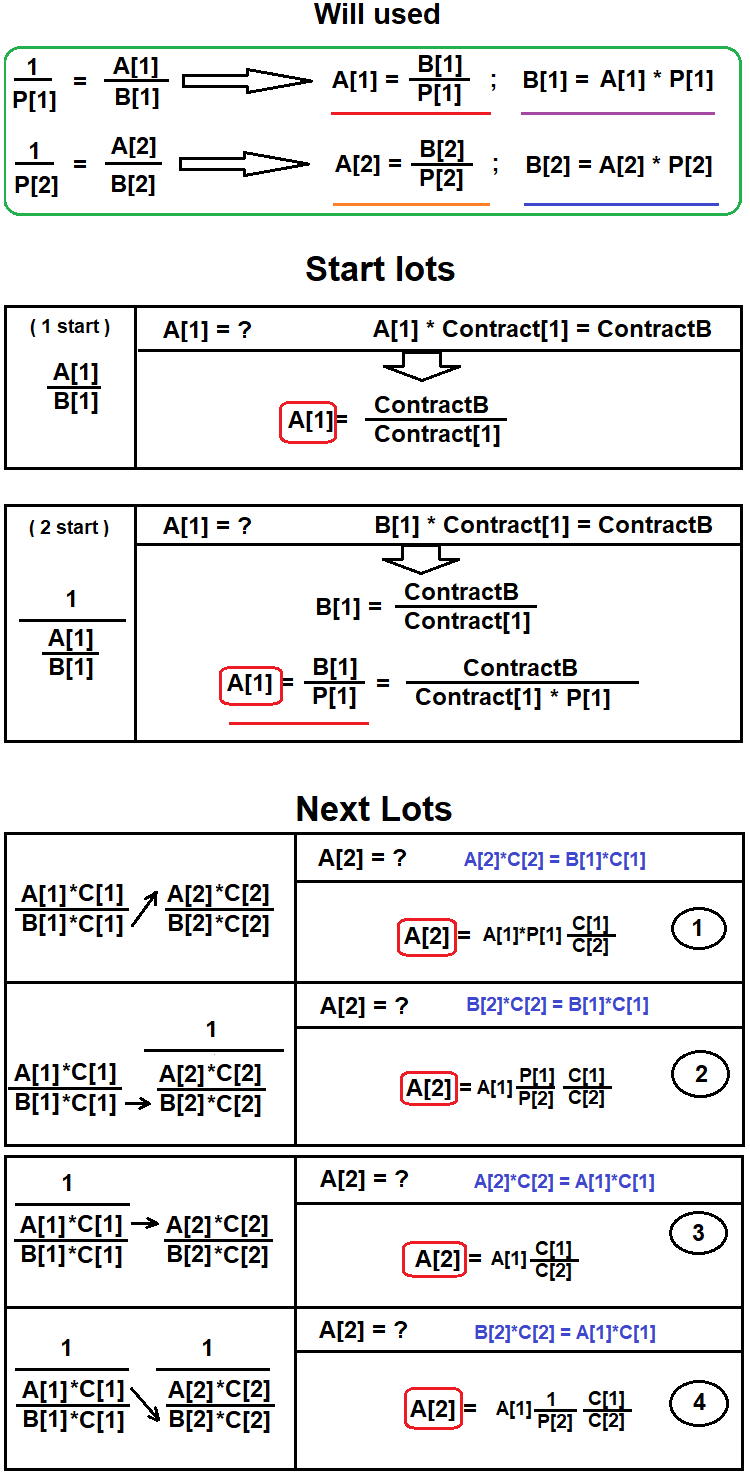
이제 이러한 기술을 코드에 구현하고 결과를 분석해 보겠습니다. 첫 번째 프로토타입은 아이디어의 정확성을 평가하는 것이므로 매우 간단합니다. 위의 다이어그램이 아이디어의 모든 세부 사항을 이해하는 데 도움이 되길 바랍니다.
스왑 폴리곤을 검사하는 유틸리티 작성하기
종합 시세 정렬 및 데이터 준비:
이 기술을 사용하려면 이름이 정확히 6자 길이이고 대문자로만 구성된 쌍만 선택해야 합니다. 모든 브로커가 이러한 이름 지정 규칙을 준수하는 것으로 알고 있습니다. 일부 브로커는 여기에 접두사 또는 접미사를 추가하는데 문자열 데이터로 작업하기 위한 알고리즘을 작성할 때도 이 점을 고려해야 합니다. 심볼 정보를 편리한 형식으로 저장하기 위해 저는 두 가지 구조를 만들었습니다(두 번째 구조는 나중에 사용할 예정입니다):
struct Pair// required symbol information { string Name;// currency pair double SwapBuy;// buy swap double SwapSell;// sell swap double TickValue;// profit from 1 movement tick of a 1-lot position double TickSize;// tick size in the price double PointX;// point size in the price double ContractSize;// contract size in the base deposit currency double Margin;// margin for opening 1 lot }; struct PairAdvanced : Pair// extended container { string Side;// in numerator or denominator double LotK;// lot coefficient double Lot;// lot };
일부 필드는 쌍을 정렬할 때 사용되지 않습니다. 불필요한 컨테이너를 만들지 않기 위해 다른 용도로도 사용할 수 있도록 구조를 조금 확장했습니다. 저는 비슷한 알고리즘의 프로토타입도 만들었었지만 기능이 매우 제한적이었습니다: 메인 터미널 창에 있는 쌍만 고려할 수 있었습니다. 이제 모든 것이 더 간단 해졌습니다. 더 중요한 것은 모든 작업이 알고리즘에서 자동화된다는 점입니다. 상품들로 배열의 크기를 설정하려면 다음 함수가 필요합니다:
Pair Pairs[];// data of currency pairs void SetSizePairsArray()// set size of the array of pairs { ArrayResize(Pairs,MaxSymbols); ArrayResize(BasicPairsLeft,MaxPairs*2); // since each pair has 2 currencies, there can be a maximum of 2 times more base currencies ArrayResize(BasicPairsRight,MaxPairs*2);// since each pair has 2 currencies, there can be a maximum of 2 times more base currencies }
첫 번째 줄은 종합시세 창에서 사용할 수 있는 최대 쌍의 수를 설정합니다. 나머지 두 줄은 사용할 배열의 크기를 설정합니다. 나머지 2개의 배열은 보조적인 역할을 합니다 - 통화 쌍을 2개의 부분(2개의 복합 통화)으로 분할할 수 있습니다. 노란색으로 강조 표시된 변수는 EA의 입력 매개변수입니다.
- MaxSymbols - 최대 쌍 저장 크기 (저는 수동으로 사양을 구현했습니다.)
- MaxPairs - 생성하는 공식의 두 부분의 최대 쌍 수(이 수보다 긴 공식은 EA에서 검색되지 않습니다).
거래 상품이 기준(다른 상품에 잠재적으로 존재할 수 있는 두 가지 통화의 징후)을 충족하는지 확인하기 위해 다음과 같은 조건자 함수를 만들었습니다:
bool IsValid(string s)// checking the instrument validity (its name must consist of upper-case letters) { string Mask="abcdefghijklmnopqrstuvwxyz1234567890";// mask of unsupported characters (lowercase letters and numbers) for ( int i=0; i<StringLen(s); i++ )// reset symbols { for ( int j=0; j<StringLen(Mask); j++ ) { if ( s[i] == Mask[j] ) return false; } } return true; }
이 함수가 향후 상품 겁사를 하기 위한 유일한 조건은 아닙니다. 그러나 이 조건은 논리 표현식 안에 작성할 수 없으므로 조건자로 구현하는 것이 더 쉽습니다. 이제 배열을 필요한 데이터로 채우는 메인 함수로 넘어가 보겠습니다:
void FillPairsArray()// fill the array with required information about the instruments { int iterator=0; double correction; int TempSwapMode; for ( int i=0; i<ArraySize(Pairs); i++ )// reset symbols { Pairs[iterator].Name=""; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { TempSwapMode=int(SymbolInfoInteger(Pairs[iterator].Name,SYMBOL_SWAP_MODE)); if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) && SymbolInfoInteger(SymbolName(i,false),SYMBOL_TRADE_MODE) == SYMBOL_TRADE_MODE_FULL && ( ( TempSwapMode == 1 ) || ( ( TempSwapMode == 5 || TempSwapMode == 6 ) && CorrectedValue(Pairs[iterator].Name,correction) )) ) { if ( iterator >= ArraySize(Pairs) ) break; Pairs[iterator].Name=SymbolName(i,false); Pairs[iterator].TickSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_SIZE); Pairs[iterator].PointX=SymbolInfoDouble(Pairs[iterator].Name, SYMBOL_POINT); Pairs[iterator].ContractSize=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_CONTRACT_SIZE); switch(TempSwapMode) { case 1:// in points Pairs[iterator].SwapBuy=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); Pairs[iterator].SwapSell=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*Pairs[iterator].TickValue*(Pairs[iterator].PointX/Pairs[iterator].TickSize); break; case 5:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; case 6:// in percent Pairs[iterator].SwapBuy=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_LONG)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); Pairs[iterator].SwapSell=correction*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_SWAP_SHORT)*SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_BID)*Pairs[iterator].ContractSize/(360.0*100.0); break; } Pairs[iterator].Margin=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_MARGIN_INITIAL); Pairs[iterator].TickValue=SymbolInfoDouble(Pairs[iterator].Name,SYMBOL_TRADE_TICK_VALUE); iterator++; } } }
이 함수는 모든 심볼을 간단하게 반복하고 문자열 이름 길이 요건 준수 여부와 해당 심볼의 거래 가능성과 스왑 계산 방식이 가장 일반적으로 사용되는 '포인트'와 다른 심볼과 관련된 기타 매개변수를 모두 확인하는 복잡한 복합 조건으로 필터링하는 기능을 제공합니다. 스왑 계산 메서드 중 하나가 '스위치' 블록에서 선택됩니다. 현재 포인트와 퍼센트의 두 가지 메서드가 구현되어 있습니다. 적절한 정렬은 주로 불필요한 계산을 피하는 데 중요합니다. 또한 빨간색으로 강조 표시된 함수에 주목하세요. 베이직 통화가 아닌 메인 통화가 증거금 통화와 일치하지 않는 통화로 표시되는 경우 특정 조정 계수를 추가하여 증거금 통화로 스왑해야 합니다. 이 함수는 관련 값들을 계산합니다. 코드는 다음과 같습니다:
bool CorrectedValue(string Pair0,double &rez)// adjustment factor to convert to deposit currency for the percentage swap calculation method { string OurValue=AccountInfoString(ACCOUNT_CURRENCY);// deposit currency string Half2Source=StringSubstr(Pair0,PrefixE+3,3);// lower currency of the pair to be adjusted if ( Half2Source == OurValue ) { rez=1.0; return true; } for ( int i=0; i<SymbolsTotal(false); i++ )// check symbols from the MarketWatch window { if ( StringLen(SymbolName(i,false)) == 6+PrefixE+PostfixE && IsValid(SymbolName(i,false)) )//find the currency rate to convert to the account currency { string Half1=StringSubstr(SymbolName(i,false),PrefixE,3); string Half2=StringSubstr(SymbolName(i,false),PrefixE+3,3); if ( Half2 == OurValue && Half1 == Half2Source ) { rez=SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } if ( Half1 == OurValue && Half2 == Half2Source ) { rez=1.0/SymbolInfoDouble(SymbolName(i,false),SYMBOL_BID); return true; } } } return false; }
이 함수는 조건자 역할을 할 뿐만 아니라 외부에서 참조로 전달된 변수에 대해 조정 계수 값을 반환합니다. 조정 계수는 증거금 통화를 포함한 원하는 통화의 환율을 기준으로 계산됩니다.
무작위로 생성된 공식
배열이 필요한 데이터로 채워졌다고 가정해 보겠습니다. 이제 어떻게든 이 심볼들을 반복해서 살펴보고 이 쌍으로 만들 수 있는 모든 가능한 수식 조합을 즉석에서 만들어야 합니다. 먼저 수식을 어떤 형태로 저장할지 결정해야 합니다. 이 공식의 모든 요소를 저장하는 구조는 사용자가 로그를 볼 필요가 있을 때를 대비하여 매우 간단하고 명확해야 합니다(그렇지 않으면 오류를 식별하는 것이 불가능합니다).
이 공식은 "=" 기호의 왼쪽과 오른쪽에 있는 요소들의 집합입니다. 계수는 1 또는 -1의 거듭제곱 환율(역분수 또는 현재 상품 환율을 나타내는 단위에 해당)일 수 있습니다. 저는 다음과 같은 구조를 사용하기로 결정했습니다:
struct EquationBasic // structure containing the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula };
모든 데이터는 문자열 형식으로 저장됩니다. 수식을 알아보기 위해 이러한 문자열을 파싱하여 필요한 모든 정보를 추출합니다. 또한 필요할 때마다 인쇄할 수 있습니다. 생성된 수식은 다음과 같은 형식으로 인쇄됩니다:
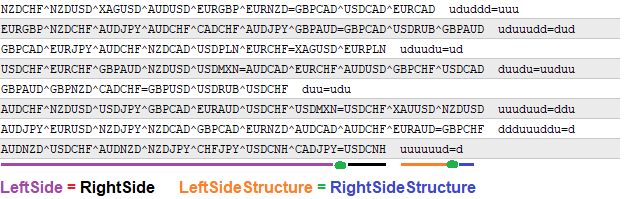
개인적으로 그런 기록은 정말 명확하고 가독성이 높습니다. 문자 "^”는 쌍을 구분하는 구분자로 사용됩니다. 수식 구조는 승수의 정도를 나타내는 단일 문자 "u" 와 "d”로 구성되므로 구분자가 필요하지 않습니다:
- "u"는 환율입니다.
- "d"는 1/환율
보시다시피 결과 수식은 방정식의 양변의 플로팅 길이와 플로팅 크기를 가지지만 이 크기에는 한계가 있습니다. 이 접근 방식은 생성된 수식의 가변성을 극대화합니다. 이와 같은 방식은 선택한 브로커의 거래 조건 내에서 발견되는 변종에 대해 가능한 최고의 품질을 제공합니다. 브로커는 완전히 다른 조건을 제시합니다. 이러한 수식을 성공적으로 생성하려면 필요한 범위의 숫자를 생성할 수 있는 추가의 무작위 함수가 필요합니다. 이를 위해 기본 제공되는 MathRand 함수의 기능을 사용하여 관련 기능을 만들어 보겠습니다:
int GenerateRandomQuantityLeftSide()// generate a random number of pairs on the left side of the formula { int RandomQuantityLeftSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-1))); if ( RandomQuantityLeftSide >= MaxPairs ) return MaxPairs-1; return RandomQuantityLeftSide; } int GenerateRandomQuantityRightSide(int LeftLenght)// generate a random number of pairs on the right side of the formula (taking into account the number of pairs on the left side) { int RandomQuantityRightSide=1+int(MathFloor((double(MathRand())/32767.0)*(MaxPairs-LeftLenght))); if ( RandomQuantityRightSide < 2 && LeftLenght == 1 ) return 2;// there must be at least 2 pairs in one of the sides, otherwise it will be equivalent to opening two opposite positions if ( RandomQuantityRightSide > (MaxPairs-LeftLenght) ) return (MaxPairs-LeftLenght); return RandomQuantityRightSide; } int GenerateRandomIndex()// generate a random index of a symbol from the MarketWatch window { int RandomIndex=0; while(true) { RandomIndex=int(MathFloor((double(MathRand())/32767.0) * double(MaxSymbols)) ); if ( RandomIndex >= MaxSymbols ) RandomIndex=MaxSymbols-1; if ( StringLen(Pairs[RandomIndex].Name) > 0 ) return RandomIndex; } return RandomIndex; }
특정 단계에서는 세 가지 함수가 모두 필요합니다. 이제 우리는 이러한 수식을 생성하는 함수를 작성할 수 있습니다. 코드는 점점 더 복잡해질 것이지만 작업이 표준은 아니기 때문에 객체 지향 접근 방식을 사용하지는 않을 것입니다. 저는 절차적 접근 방식을 사용하기로 결정했습니다. 결과적인 절차는 상당히 크고 번거롭지만 추가 기능이 없으며 코드 중복을 피하기 위해 각 함수는 중간 함수를 사용하지 않고 특정 작업을 구현합니다. 그렇지 않으면 작업의 특성으로 인해 코드는 이해하기 훨씬 더 어려워질 것입니다. 함수는 다음과 같이 표시됩니다:
EquationBasic GenerateBasicEquation()// generate both parts of the random equation { int RandomQuantityLeft=GenerateRandomQuantityLeftSide(); int RandomQuantityRight=GenerateRandomQuantityRightSide(RandomQuantityLeft); string TempLeft=""; string TempRight=""; string TempLeftStructure=""; string TempRightStructure=""; for ( int i=0; i<RandomQuantityLeft; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == 0 && RandomQuantityLeft > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i != 0 && (RandomQuantityLeft-i) > 1 ) TempLeft+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft-1 ) TempLeft+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempLeftStructure+="u"; else TempLeftStructure+="d"; } for ( int i=RandomQuantityLeft; i<RandomQuantityLeft+RandomQuantityRight; i++ ) { int RandomIndex=GenerateRandomIndex(); if ( i == RandomQuantityLeft && RandomQuantityRight > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i != RandomQuantityLeft && (RandomQuantityLeft+RandomQuantityRight-i) > 1 ) TempRight+=Pairs[RandomIndex].Name+"^"; if ( i == RandomQuantityLeft+RandomQuantityRight-1 ) TempRight+=Pairs[RandomIndex].Name; if ( double(MathRand())/32767.0 > 0.5 ) TempRightStructure+="u"; else TempRightStructure+="d"; } EquationBasic result; result.LeftSide=TempLeft; result.LeftSideStructure=TempLeftStructure; result.RightSide=TempRight; result.RightSideStructure=TempRightStructure; return result; }
보시다시피 앞서 고려한 세 가지 함수가 모두 임의의 공식을 생성하는 데 사용됩니다. 이러한 함수는 코드의 다른 곳에서는 사용되지 않습니다. 공식이 준비되면 우리는 이 공식에 대한 단계별 분석을 진행할 수 있습니다. 잘못된 공식은 모두 다음의 매우 중요한 복잡한 필터에 의해 삭제됩니다. 우선 형평성을 확인합니다. 부분들이 같지 않으면 이 공식은 올바르지 않습니다. 모든 공식은 다음 분석 단계로 진행됩니다.
포뮬러 밸런싱
이 단계에서는 여러 분석 기준을 한 번에 다룹니다:
- 분자와 분모에 있는 모든 추가 요인을 계산하고 제거합니다.
- 분자에 1개 통화, 분모에 1개 통화 사용 가능 여부 확인
- 왼쪽과 오른쪽에서 결과 분수의 대응을 확인
- 오른쪽이 왼쪽의 역수인 경우 수식의 오른쪽 구조를 뒤집으면 됩니다(이는 "-1"의 거듭제곱과 유사합니다).
- 모든 단계가 성공적으로 완료되면 결과가 새 변수에 기록됩니다.
이러한 단계가 코드에 표시되는 방식은 다음과 같습니다:
BasicValue BasicPairsLeft[];// array of base pairs to the left BasicValue BasicPairsRight[];// array of base pairs to the right bool bBalanced(EquationBasic &CheckedPair,EquationCorrected &r)// if the current formula is balanced (if yes, return the corrected version to the "r" variable) { bool bEnd=false; string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } //// Calculate balance values for the left side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(CheckedPair.LeftSide,i,1); if ( Divider == "^" || i == StringLen(CheckedPair.LeftSide) - 1 ) { SubPair=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.LeftSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of left-side balance calculation //// Calculate balance values for the right side quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(CheckedPair.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(CheckedPair.RightSide,i,1); if ( Divider == "^"|| i == StringLen(CheckedPair.RightSide) - 1 ) { SubPair=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(CheckedPair.RightSideStructure,quantityiterator,1); Half1=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(CheckedPair.RightSide,ReadStartIterator+PrefixE+3,3); bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } ReadStartIterator=i+1; quantityiterator++; } } /// end of right-side balance calculation /// calculate the number of lower and upper currencies based on the received data from the previous block int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpLeft; string LastDownLeft; string LastUpRight; string LastDownRight; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity > 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[i].Quantity; if ( BasicPairsLeft[i].Quantity < 0 && StringLen(BasicPairsLeft[i].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[i].Quantity; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity > 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightUpTotal+=BasicPairsRight[i].Quantity; if ( BasicPairsRight[i].Quantity < 0 && StringLen(BasicPairsRight[i].Value) > 0 ) RightDownTotal-=BasicPairsRight[i].Quantity; } /// /// check if both sides are equal if ( LeftUpTotal == 1 && LeftDownTotal == 1 && RightUpTotal == 1 && RightDownTotal == 1 )// there must be one pair in the upper and in the lower part of both sides of the equality, otherwise the formula is invalid { for ( int i=0; i<ArraySize(BasicPairsLeft); i++ ) { if ( BasicPairsLeft[i].Quantity == 1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastUpLeft=BasicPairsLeft[i].Value; if ( BasicPairsLeft[i].Quantity == -1 && StringLen(BasicPairsLeft[i].Value) > 0 ) LastDownLeft=BasicPairsLeft[i].Value; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ ) { if ( BasicPairsRight[i].Quantity == 1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastUpRight=BasicPairsRight[i].Value; if ( BasicPairsRight[i].Quantity == -1 && StringLen(BasicPairsRight[i].Value) > 0 ) LastDownRight=BasicPairsRight[i].Value; } } else return false; if ( (LastUpLeft == LastUpRight && LastDownLeft == LastDownRight) || (LastUpLeft == LastDownRight && LastDownLeft == LastUpRight) ) { if ( LastUpLeft == LastDownRight && LastDownLeft == LastUpRight )// If the formula is cross-equivalent, then invert the structure of the right part of the equation (it is the same as raising to the power of -1) { string NewStructure;// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; } } else return false;// if the resulting fractions on both sides are not equivalent, then the formula is invalid if ( LastUpLeft == LastDownLeft ) return false;// if result in one, then the formula is invalid /// Now it is necessary to write all the above into a corrected and more convenient structure string TempResult=CorrectedResultInstrument(LastUpLeft+LastDownLeft,r.IsResultInstrument); if ( r.IsResultInstrument && LastUpLeft+LastDownLeft != TempResult ) { string NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.RightSideStructure); i++ ) { if ( CheckedPair.RightSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.RightSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.RightSideStructure=NewStructure; NewStructure="";// the new structure that will be built from the previous one for ( int i=0; i<StringLen(CheckedPair.LeftSideStructure); i++ ) { if ( CheckedPair.LeftSideStructure[i] == 'u' ) NewStructure+="d"; if ( CheckedPair.LeftSideStructure[i] == 'd' ) NewStructure+="u"; } CheckedPair.LeftSideStructure=NewStructure; r.ResultInstrument=LastDownLeft+LastUpLeft; r.UpPair=LastDownLeft; r.DownPair=LastUpLeft; } else { r.ResultInstrument=LastUpLeft+LastDownLeft; r.UpPair=LastUpLeft; r.DownPair=LastDownLeft; } r.LeftSide=CheckedPair.LeftSide; r.RightSide=CheckedPair.RightSide; r.LeftSideStructure=CheckedPair.LeftSideStructure; r.RightSideStructure=CheckedPair.RightSideStructure; /// /// if code has reached this point, it is considered that we have found the formula meeting the criteria, and the next step is normalization return true; }
녹색으로 강조 표시된 함수는 심볼 목록에 수식이 축소된 심볼이 포함되어 있는지를 확인하기 위해 필요합니다. 예를 들어 공식이 'USDJPY'가 아닌 'JPYUSD'로 축소된 것으로 나타날 수 있습니다. 이러한 심볼은 생성될 수는 있지만 분명히 존재하지는 않습니다. 그러나 우리의 임무는 올바른 거래 상품을 생성하도록 공식을 수정하는 것입니다. 이 경우 공식의 두 부분을 -1의 거듭제곱으로 높여야 하며 이는 공식의 구조를 뒤집는 것과 같습니다("d"를 "u"로 또는 그 반대로 변경). 종합시세 창에 해당 심볼이 없으면 그대로 둡니다:
string CorrectedResultInstrument(string instrument, bool &bResult)// if any equivalent symbol corresponds to the generated formula, return this symbol (or leave as is) { string Half1=""; string Half2=""; string Half1input=StringSubstr(instrument,0,3);//input upper currency string Half2input=StringSubstr(instrument,3,3);//input lower currency bResult=false; for ( int j=0; j<ArraySize(Pairs); j++ ) { Half1=StringSubstr(Pairs[j].Name,PrefixE,3); Half2=StringSubstr(Pairs[j].Name,PrefixE+3,3); if ( (Half1==Half1input && Half2==Half2input) || (Half1==Half2input && Half2==Half1input) )// direct match or crossed match { bResult=true; return Pairs[j].Name; } } return instrument; }
저는 필터를 통과한 수식을 저장하기 위해 다음과 같은 구조를 준비했습니다. 이 구조에는 이전 구조의 일부 필드와 새로운 필드가 있습니다:
struct EquationCorrected // corrected structure of the basic formula { string LeftSide;// currency pairs participating in the formula on the left side of the "=" sign string LeftSideStructure;// structure of the left side of the formula string RightSide;// currency pairs participating in the right side of the formula string RightSideStructure;// structure of the right side of the formula string ResultInstrument;// the resulting instrument to which both parts of the formula come after transformation bool IsResultInstrument;// has the suitable equivalent symbol been found string UpPair;// the upper currency of the resulting instrument string DownPair;// the lower currency of the resulting instrument };
수식 정규화
이 절차는 결과를 필터링하는 다음 단계입니다. 다음과 같은 순차적인 작업으로 구성되며 이 작업은 차례로 이어집니다:
- 방정식의 양쪽에서 얻은 결과 심볼을 바탕으로 등식의 양쪽 목록에서 시작 쌍을 선택합니다.
- 두 쌍은 방정식의 힘에 따라 분수 분자에 베이스 통화를 제공해야 합니다.
- 이러한 쌍이 발견되고 분수의 하위 통화가 결과 상품의 메인 통화를 포함하지 않으면 더 진행하십시오.
- 또한 다음 쌍의 상위 통화가 이전 쌍의 하위 통화를 보상하도록 진행합니다.
- 원하는 결과 쌍을 찾을 때까지 이 단계를 반복합니다.
- 결과 쌍이 발견되면 사용하지 않은 공식의 모든 구성 요소는 무시됩니다(해당 상품은 하나이므로).
- 이 과정과 병행하여 "랏 팩터"가 쌍에서 쌍까지 순차적으로 계산됩니다(특정 쌍에 대해 어떤 랏으로 포지션에 진입해야 하는지 표시하여 결과 상품을 보장합니다).
- 결과는 다음 분석 단계에서 사용될 새로운 변수에 기록됩니다.
함수 코드는 다음과 같습니다:
bool bNormalized(EquationCorrected &d,EquationNormalized &v)// formula normalization attempt (the normalized formula is returned in "v" ) { double PreviousContract;// previous contract bool bWasPairs;// if any pairs have been found double BaseContract;// contract of the pair to which the equation is reduced double PreviousLotK=0.0;// previous LotK double LotK;// current LotK string PreviousSubSide;// in numerator or denominator (previous factor) string PreviousPair;// previous pair string PreviousHalf1;// upper currency of the previous pair string PreviousHalf2;// lower currency of the previous pair string SubPair;// the full name of the currency pair string Half1;// the first currency of the pair string Half2;// the second currency of the pair string SubSide;// the currency pair in the numerator or denominator string Divider;// separator int ReadStartIterator=0;// reading start index int quantityiterator=0;// quantity int tryiterator=0;// the number of balancing attempts int quantityleft=0;// the number of pairs on the left after normalization int quantityright=0;//the number of pairs on the right after normalization bool bNew; BasicValue b0; for ( int i=0; i<ArraySize(BasicPairsLeft); i++ )//reset the array of base pairs { BasicPairsLeft[i].Value = ""; BasicPairsLeft[i].Quantity = 0; } for ( int i=0; i<ArraySize(BasicPairsRight); i++ )// resetting the array of base pairs { BasicPairsRight[i].Value = ""; BasicPairsRight[i].Quantity = 0; } if ( d.IsResultInstrument ) BaseContract=SymbolInfoDouble(d.ResultInstrument, SYMBOL_TRADE_CONTRACT_SIZE);// define the contract of the equivalent pair based on the instrument else BaseContract=100000.0; //// Calculate the number of pairs for the left side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.LeftSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } /// end of quantity calculation for the left part ArrayResize(v.PairLeft,tryiterator); /// calculate the lot coefficients for the left side bool bBalanced=false;// is the formula balanced bool bUsed[]; ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); int balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false;// have there been pairs for ( int k=0; k<tryiterator; k++ )// try to normalize the left side { if( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.LeftSide); i++ )// extract base currencies from the left side of the equation { Divider=StringSubstr(d.LeftSide,i,1); if ( Divider == "^" || i == StringLen(d.LeftSide) - 1 ) { SubPair=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.LeftSideStructure,quantityiterator,1); Half1=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.LeftSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 1 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 2 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 3 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// ( 4 ) v.PairLeft[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity++; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity--; BasicPairsLeft[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( BasicPairsLeft[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsLeft[j].Quantity--; if ( SubSide == "d" ) BasicPairsLeft[j].Quantity++; BasicPairsLeft[j].Value=Half2; break; } } } v.PairLeft[balancediterator].Name=SubPair; v.PairLeft[balancediterator].Side=SubSide; v.PairLeft[balancediterator].ContractSize=SymbolInfoDouble(v.PairLeft[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityleft++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int LeftUpTotal=0;// the number of upper elements in the left part int LeftDownTotal=0;// the number of lower elements in the left part string LastUpLeft; string LastDownLeft; for ( int z=0; z<ArraySize(BasicPairsLeft); z++ ) { if ( BasicPairsLeft[z].Quantity > 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftUpTotal+=BasicPairsLeft[z].Quantity; if ( BasicPairsLeft[z].Quantity < 0 && StringLen(BasicPairsLeft[z].Value) > 0 ) LeftDownTotal-=BasicPairsLeft[z].Quantity; } if ( bWasPairs && LeftUpTotal == 0 && LeftDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } /// end of coefficient calculation for the left part if ( !bBalanced ) return false;// if the left side is not balanced, then there is no point in balancing the right side //// Calculate the number of pairs for the right side tryiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" ) { ReadStartIterator=i+1; tryiterator++; } if ( i == StringLen(d.RightSide) - 1 ) { ReadStartIterator=i+1; tryiterator++; } } ArrayResize(v.PairRight,tryiterator); /// end of calculation of the number of pairs for the right side bBalanced=false;// is the formula balanced ArrayResize(bUsed,tryiterator); ArrayFill(bUsed,0,tryiterator,false); balancediterator=0; PreviousHalf1=""; PreviousHalf2=""; PreviousLotK=0.0; PreviousSubSide=""; PreviousPair=""; PreviousContract=0.0; bWasPairs=false; for ( int k=0; k<tryiterator; k++ )// try to normalize the right side { if ( !bBalanced ) { quantityiterator=0; ReadStartIterator=0; for ( int i=ReadStartIterator; i<StringLen(d.RightSide); i++ )// extract base currencies from the right side of the equation { Divider=StringSubstr(d.RightSide,i,1); if ( Divider == "^" || i == StringLen(d.RightSide) - 1 ) { SubPair=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,6); SubSide=StringSubstr(d.RightSideStructure,quantityiterator,1); Half1=StringSubstr(d.RightSide,ReadStartIterator+PrefixE,3); Half2=StringSubstr(d.RightSide,ReadStartIterator+PrefixE+3,3); if ( ! bUsed[quantityiterator] && (( PreviousHalf1 == "" && ((Half1 == d.UpPair && SubSide == "u") || (Half2 == d.UpPair && SubSide == "d")) ) // if it is the first pair in the list || ( (( PreviousHalf2 == Half1 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half1 && PreviousSubSide == "d" )) && SubSide == "u" ) // if the current pair is in the numerator || ( (( PreviousHalf2 == Half2 && PreviousSubSide == "u" ) || ( PreviousHalf1 == Half2 && PreviousSubSide == "d" )) && SubSide == "d" )) )// if the current pair is in the denominator {// find the entry point(pair) of the chain if( PreviousHalf1 == "" )// define the lot coefficient of the first pair { if ( SubSide == "u" ) { LotK=BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE);// (1 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; LotK=(BaseContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE))/Pt;// (2 start) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; bWasPairs=true; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } else { if( PreviousSubSide == "u" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*Pp*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (1) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); double Pp=SymbolInfoDouble(PreviousPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( Pp == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(Pp/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (2) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } if( PreviousSubSide == "d" )// define the lot coefficient of further pairs { if ( SubSide == "u" ) { if ( PreviousContract <= 0.0 ) return false; LotK=PreviousLotK*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (3) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } if ( SubSide == "d" ) { double Pt=SymbolInfoDouble(SubPair,SYMBOL_BID); if ( Pt == 0.0 ) return false; if ( PreviousContract <= 0.0 ) return false; LotK=(PreviousLotK/Pt)*(PreviousContract/SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE));// (4) v.PairRight[balancediterator].LotK=LotK; PreviousLotK=LotK; PreviousContract=SymbolInfoDouble(SubPair, SYMBOL_TRADE_CONTRACT_SIZE); } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half1 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsLeft); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsLeft[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity++; if ( SubSide == "d" ) BasicPairsRight[j].Quantity--; BasicPairsRight[j].Value=Half1; break; } } } bNew=true; for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( BasicPairsRight[j].Value == Half2 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; bNew = false; break; } } if ( bNew ) { for ( int j=0; j<ArraySize(BasicPairsRight); j++ )// if the currency is not found in the list, add it { if ( StringLen(BasicPairsRight[j].Value) == 0 ) { if ( SubSide == "u" ) BasicPairsRight[j].Quantity--; if ( SubSide == "d" ) BasicPairsRight[j].Quantity++; BasicPairsRight[j].Value=Half2; break; } } } v.PairRight[balancediterator].Name=SubPair; v.PairRight[balancediterator].Side=SubSide; v.PairRight[balancediterator].ContractSize=SymbolInfoDouble(v.PairRight[balancediterator].Name, SYMBOL_TRADE_CONTRACT_SIZE); balancediterator++; PreviousHalf1=Half1; PreviousHalf2=Half2; PreviousSubSide=SubSide; PreviousPair=SubPair; quantityright++; if ( SubSide == "u" && Half2 == d.DownPair )// if the fraction is not inverted { bBalanced=true;// if the missing part is in the denominator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } if ( SubSide == "d" && Half1 == d.DownPair )// if the fraction is inverted { bBalanced=true;// if the missing part is in the numerator, then we have balanced the formula break;// since the formula is balanced, we don't need the rest } int RightUpTotal=0;// the number of upper elements in the right part int RightDownTotal=0;// the number of lower elements in the right part string LastUpRight; string LastDownRight; for ( int z=0; z<ArraySize(BasicPairsRight); z++ ) { if ( BasicPairsRight[z].Quantity > 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightUpTotal+=BasicPairsRight[z].Quantity; if ( BasicPairsRight[z].Quantity < 0 && StringLen(BasicPairsRight[z].Value) > 0 ) RightDownTotal-=BasicPairsRight[z].Quantity; } if ( bWasPairs && RightUpTotal == 0 && RightDownTotal == 0 ) return false; } ReadStartIterator=i+1; bUsed[quantityiterator]=true; quantityiterator++; } } } else break; } if ( quantityleft == 1 && quantityright == 1 ) return false;// if the equation has been normalized to only 2 pairs, it is not valid (at least 3 pairs are required) return bBalanced; }
이것은 매우 정상적이면서 복잡한 절차이지만 이러한 경우 상당한 코드의 중복으로 이어질 수 있으므로 중간 상태를 생성하지 않는 것이 더 나은 것 같습니다. 또한 모든 단계가 매우 간결하고 논리적으로 블록으로 나뉘어 있습니다. 이러한 함수의 집합은 모든 변환을 수기로 수행했을 때 얻을 수 있는 결과와 완전히 동일한 결과를 제공합니다. 여기서 이러한 모든 수학적 조작은 복잡하지만 필요한 일련의 메서드로 수행됩니다.
만든 공식이 얼마나 수익성이 있는지 알아보기 위해 우리는 특별한 분석을 수행해야 합니다. 각 쌍에 대해 위아래로 포지션을 오픈할 수 있다는 것을 잊지 마세요. 따라서 각 공식에 대해 직접 및 역방향의 두 가지 중간 단계의 서킷의 변형이 있을 수 있습니다. 이 중 수익성이 더 높은 것이 결과로 받아들여질 것입니다.
수익성을 평가하기 위해 스왑으로 인한 이익과 손실로 구성된 수익률과 유사한 지표를 만들었습니다. 기존 서킷의 누적된 포지티브 스왑이 마이너스 계수보다 크면 해당 서킷은 수익성이 있는 것으로 간주됩니다. 다른 경우에는 이러한 서킷은 수익성이 없습니다. 즉 윤곽의 스왑 계수가 1보다 클 때만 양수가 됩니다.
반환된 결과는 거래 및 거래 로직의 추가적인 개발을 위해 자급자족적인 명령 패키지로 만들어진 완전히 다른 컨테이너에 기록됩니다. 여기에는 전체 서킷을 빠르고 쉽게 여는 데 필요한 모든 것이 포함되어 있습니다:
struct EquationNormalized // the final structure with the formula in normalized form { Pair PairLeft[];// currency pairs on the left side Pair PairRight[];// currency pairs on the right side double SwapPlusRelative;// relative equivalent of the positive swap double SwapMinusRelative;// relative equivalent of the negative swap double SwapFactor;// resulting swap factor };
또한 저는 콘텐츠에 대한 정보를 편리하게 표시할 수 있는 두 가지 방법을 추가했지만 이 글과 관련이 없으므로 여기서는 제공하지 않겠습니다. 여러분은 첨부된 소스 코드에서 확인할 수 있습니다. 이제 방정식의 각 구성 요소에 대한 정보는 배열의 요소로서 개별적으로 포함됩니다. 이렇게 하면 나중에 문자열에서 데이터를 계속해서 구문 분석할 필요 없이 데이터로 더 쉽게 작업할 수 있습니다. 처음부터 이 솔루션을 사용할 수도 있지만 가독성을 떨어뜨릴 수도 있었을 것입니다.
스왑 계수 계산 및 방정식 구조의 최종 조정
이것은 이 시스템의 가장 중요한 변수가 계산되는 마지막 단계로 이 값에 따라 변형이 비교됩니다. 가장 높은 값이 가장 좋은 것입니다.
void CalculateBestVariation(EquationNormalized &ii)// calculation of the best swap factor of the formula and final structure adjustment if needed { double SwapMinus=0.0;// total negative swap double SwapPlus=0.0;// total positive swap double SwapMinusReverse=0.0;// total negative swap double SwapPlusReverse=0.0;// total positive swap double SwapFactor=0.0;// swap factor of the direct pass double SwapFactorReverse=0.0;// swap factor of the reverse pass for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// define the missing parameters for calculating the left side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairLeft[i].Name ) { ii.PairLeft[i].Margin=Pairs[j].Margin; ii.PairLeft[i].TickValue=Pairs[j].TickValue; ii.PairLeft[i].SwapBuy=Pairs[j].SwapBuy; ii.PairLeft[i].SwapSell=Pairs[j].SwapSell; break; } } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// define the missing parameters for calculating the right side { for ( int j=0; j<ArraySize(Pairs); j++ ) { if ( Pairs[j].Name == ii.PairRight[i].Name ) { ii.PairRight[i].Margin=Pairs[j].Margin; ii.PairRight[i].TickValue=Pairs[j].TickValue; ii.PairRight[i].SwapBuy=Pairs[j].SwapBuy; ii.PairRight[i].SwapSell=Pairs[j].SwapSell; break; } } } double TempSwap; // calculate all components taking into account a change in the structure for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// for left parts { if ( ii.PairLeft[i].Side == "u" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairLeft[i].Side == "d" ) {// for direct trading TempSwap=ii.PairLeft[i].SwapSell*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairLeft[i].SwapBuy*ii.LotKLeft[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } for ( int i=0; i<ArraySize(ii.PairRight); i++ )// for right parts { if ( ii.PairRight[i].Side == "d" ) {// for direct trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } if ( ii.PairRight[i].Side == "u" ) {// for direct trading TempSwap=ii.PairRight[i].SwapSell*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlus+=TempSwap; else SwapMinus-=TempSwap; // for reverse trading TempSwap=ii.PairRight[i].SwapBuy*ii.LotKRight[i]; if ( TempSwap >= 0 ) SwapPlusReverse+=TempSwap; else SwapMinusReverse-=TempSwap; } } // calculate the swap factor for the direct pass if ( SwapMinus > 0.0 && SwapPlus > 0.0 ) SwapFactor=SwapPlus/SwapMinus; if ( SwapMinus == 0.0 && SwapPlus == 0.0 ) SwapFactor=1.0; if ( SwapMinus == 0.0 && SwapPlus > 0.0 ) SwapFactor=1000001.0; if ( SwapMinus > 0.0 && SwapPlus == 0.0 ) SwapFactor=0.0; // calculate the swap factor for the reverse pass if ( SwapMinusReverse > 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=SwapPlusReverse/SwapMinusReverse; if ( SwapMinusReverse == 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=1.0; if ( SwapMinusReverse == 0.0 && SwapPlusReverse > 0.0 ) SwapFactorReverse=1000001.0; if ( SwapMinusReverse > 0.0 && SwapPlusReverse == 0.0 ) SwapFactorReverse=0.0; // select the best approach and calculate the missing values in the structure if ( SwapFactor > SwapFactorReverse ) { ii.SwapPlusRelative=SwapPlus; ii.SwapMinusRelative=SwapMinus; ii.SwapFactor=SwapFactor; } else { ii.SwapPlusRelative=SwapPlusReverse; ii.SwapMinusRelative=SwapMinusReverse; ii.SwapFactor=SwapFactorReverse; bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// if it is a reverse pass, then reverse the right structure of the formula { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } bSigned=false; for ( int i=0; i<ArraySize(ii.PairLeft); i++ )// if it is a reverse pass, then reverse the left structure of the formula { bSigned=false; if ( !bSigned && ii.PairLeft[i].Side == "u" ) { ii.PairLeft[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairLeft[i].Side == "d" ) { ii.PairLeft[i].Side="u"; bSigned=true; } } } bool bSigned; for ( int i=0; i<ArraySize(ii.PairRight); i++ )// reverse the right side anyway { bSigned=false; if ( !bSigned && ii.PairRight[i].Side == "u" ) { ii.PairRight[i].Side="d"; bSigned=true; } if ( !bSigned && ii.PairRight[i].Side == "d" ) { ii.PairRight[i].Side="u"; bSigned=true; } } }
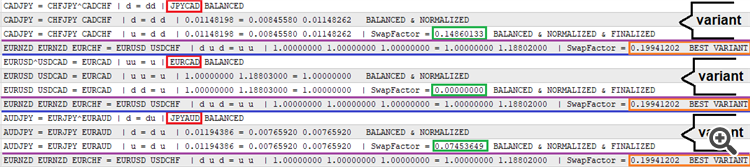
저는 결과를 순차적으로 출력할 수 있도록 필터링에 성공한 수식 변형이 발견된 경우에만 기록되는 로그를 구현했습니다. 로그는 다음과 같습니다:
결과 심볼에는 빨간색이 사용되며 방정식의 양쪽이 줄어듭니다. 다음 줄은 랏 계수가 있는 정규화된 변형을 보여줍니다. 세 번째 줄은 계산된 스왑 계수가 있는 변형을 표시합니다. 네 번째 줄은 무차별 대입 세션에서 발견된 변형 중 가장 좋은 변형이며 코멘트 함수를 통해 그려진 차트에도 표시됩니다. 이 프로토타입은 아래에 첨부되어 있습니다. 여러분이 직접 테스트해 볼 수 있으며 실제로 스왑 트레이딩을 위한 트레이딩 도우미의 프로토타입 역할을 할 수 있습니다. 지금은 기능이 거의 없지만 다음 글에서 기능을 확장해 보도록 하겠습니다. MetaTrader 4와 MetaTrader 5용 프로토타입은 두 가지 버전으로 제공됩니다.
첫 번째 테스트로부터의 결론
이러한 복잡한 주제에 대해 혼자서 결론을 내리는 것은 매우 어렵습니다. 저는 아직까지 1보다 큰 스왑 계수를 찾지 못했지만 유용한 것들을 이해할 수 있었습니다. 이것이 제가 이 프로토타입의 작업을 분석하면서 내린 첫 번째 결론입니다:
- 일부 통화쌍의 경우 포지션이 합성 등가물로 표시되기 때문에 포지티브 스왑을 늘리거나 마이너스 스왑을 줄일 수 있습니다(포지션이 합성 등가물로 표시되기 때문에).
- 수익성 있는 서킷을 찾지 못하더라도 이들중 어느 부분은 두 개의 다른 트레이딩 계좌에 고정하는 대체 포지션으로 언제든지 사용할 수 있습니다.
- 이러한 합성 포지션으로 잠그면 양쪽 끝에서 반대 포지션의 스왑이 가능하므로 스왑 프리 계좌를 사용할 필요가 없어집니다.
- 가장 인기있는 브로커로 기능 확장이 필요한 더 심층적 인 분석을 수행해야 합니다.
- 수익성 있는 스왑 팩터를 달성할 수 있다는 것을 증명할 수 있기를 바랍니다(지금까지는 추측일 뿐입니다).
- 스왑을 현명하게 사용하면 작지만 꾸준한 수익을 얻을 수 있습니다.
결론
이 접근 방식이 여러분에게 흥미롭고 생각할 거리를 제공할 수 있기를 바랍니다. 이 방법은 이해하기 매우 어렵지만 실제로는 동일한 볼륨으로 두 개의 반대쪽 포지션으로 진입하는 간단한 원리를 구현합니다. 이렇게 서로 반대되는 두 포지션을 오픈하는 것만으로도 항상 손실이 발생합니다. 마이너스 단방향 스왑보다 더 큰 모듈러스를 제공하는 포지티브 단방향 스왑을 제공하는 브로커는 없습니다. 물론 수학적으로 불가능하기 때문에 양방향으로 포지티브 스왑을 하는 것은 불가능합니다.
기초 수학에 대한 자세한 내용은 매우 광범위한 주제이므로 여기서 다루지는 않겠습니다. 이 수학의 표현을 활용하는 것이 좋습니다. 설명한 방법을 적용하면 포지션 잠금에서 스왑으로 인한 손실을 줄일 수 있습니다. 또한 브로커의 스왑 테이블에서 갭을 찾아 플러스 수익률(모든 포지션의 총 수익이 발생하는 스왑)로 잠금을 즐길 수 있으며 이는 가격 변동에 영향을 받지 않는 무위험 거래입니다.
포지티브 스왑이 잠재적인 수익을 제공하기 때문에 스왑 거래 방식이 과소평가되고 있다고 생각합니다. 이상 살펴본 방법은 스왑 거래 방법의 가능한 변형 중 하나 일 뿐입니다. 저는 이 작업이 마음에 들며 다음 기사에서 아이디어를 개발하고 코드를 현대화 하며 새로운 추가 기능을 만들어 보려고 합니다. 또한 수익 예측 및 트레이딩 기능에 대한 몇 가지 아이디어도 설명하겠습니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/9198
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.
 예제로 패턴 살펴보기(1부): 멀티 탑
예제로 패턴 살펴보기(1부): 멀티 탑
 Expert Advisor 개발 기초부터(31부): 미래를 향해(IV)
Expert Advisor 개발 기초부터(31부): 미래를 향해(IV)
새 문서 스왑(1부): 잠금과 합성 포지션이 게시되었습니다:
작성자: Evgeniy Ilin
기사를 작성해 주셔서 감사합니다.
기사를 보내주셔서 감사합니다.
환영합니다 ).
안녕하세요,
MT4와 MT5 모두에서 전문가를 실행했는데 PostFix가 있으면 전문가가 실행되지 않고 결과를 얻지 못합니다.
이유를 알아 내거나 수정할 수 있습니까?
많은 감사