
相場パターンを見つけるための計量的アプローチ:自己相関、ヒートマップ、散布図
以前の記事と新しいモデルを作成するための前提条件の簡単なおさらい
最初の記事では、オーダーの価格増分の長期的な依存として決定される相場メモリの概念を紹介しました。 さらに、相場に存在する「季節パターン」の概念を考えました。 これまで、この2つの概念は別々に存在してきました。 この記事の目的は、"market memory(マーケットメモリー)" が季節的性質を持ち、近くに配置された時間間隔に対して任意のオーダーの増分の最大相関を通じて表現され、遠い時間間隔の相関を最小限に抑えることを示すものです。
次の仮説を提唱しましょう。
価格増分の相関は、季節パターンの存在、および近くの増分のクラスタリングに依存します。
直感的で少し数学的なスタイルで確認または反論してみましょう。
価格増分でパターンを識別するための古典的な計量的アプローチは自己相関である
古典的なアプローチによると、価格増分のパターンの欠如は、連続相関の欠如によって決定されます。 自己相関がない場合、一連の増分はランダムと見なされますが、パターンの検索は無効であると考えられます。
自己相関関数を使用してEURUSDインクリメントの視覚的分析の例を見てみましょう。 すべての例は IPython を使用して実行されます。
def standard_autocorrelation(symbol, lag):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
standard_autocorrelation('EURUSD', 50)
この関数は、H1終値を指定期間(ラグ50が使用する)との関連差に変換し、自己相関チャートを表示します。
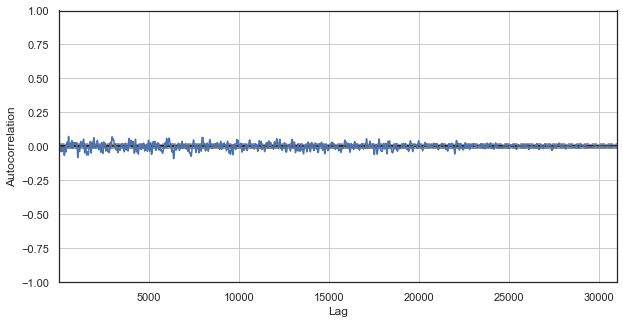
図1. 古典的な価格はコレログラムをインクリメント
自己相関チャートは価格増分のパターンを明らかにしません。 隣接する増分間の相関は、時系列のランダム性を示すゼロの周りに変動します。 相場がランダムであると結論付ければ、ここで計量分析を終了することができます。 しかし、季節パターンの文脈で、自己相関関数を異なる角度から見直す方法を提案します。
価格増分の相関関係は、季節パターンの存在によって生成することができると仮定しました。 したがって、特定の時間を除くすべての時間を例から除外しましょう。 したがって、独自の特定のプロパティを持つ新しい時系列を作成します。 この系列の自己相関関数を構築します。
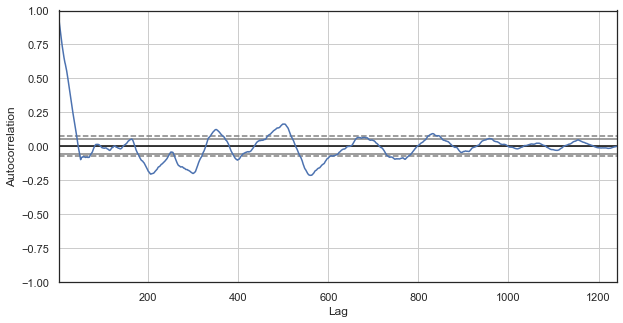
図2. 除外時間を含む価格増分のコレログラム(残りの各日の1時間目のみ)
コレログラムは新シリーズに適します。 以前のものに現在の増分の強い依存があります。 増分間の時間デルタが増加すると、依存性は減少します。 つまり、現在の 1 時間の増分は前日の 1 番目の時間の増分と強く相関します。 この重要な情報は、季節パターンの存在、すなわち増加にはメモリがあることを示します。
価格増分でパターンを識別するためのカスタムアプローチは季節的な自己相関です
現在の 1 時間の増分と前の 1 時間の増分には相関関係があり、日の間の距離が長くなると、減少することがわかりました。 次に、隣接する時間の間に相関関係があるかどうかを見てみましょう。 コードを変更してみましょう。
def seasonal_autocorrelation(symbol, lag, hour1, hour2):
rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
from pandas.plotting import autocorrelation_plot
plt.figure(figsize=(10, 5))
autocorrelation_plot(rates)
seasonal_autocorrelation('EURUSD', 50, 1, 2)
ここでは、最初と2番目を除くすべての時間を削除し、新しい系列の差を計算し、自己相関関数を構築します。
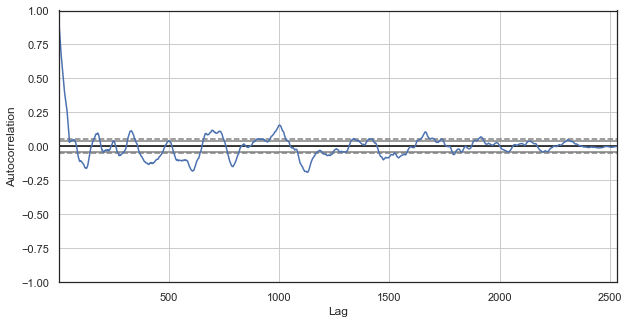
図3. 除外時間を含む価格増分のコレログラム(残りの各日の1日と2時間目のみ)
明らかに、一連の最も近い時間には高い相関もあり、相関と相互の影響を示します。 選択した時間だけでなく、すべての時間のペアに対して信頼できる相対スコアを得ることはできるでしょうか。 これを行うには、以下に説明する方法を使用します。
すべての時間の季節相関のヒートマップ
相場を探索し、元の仮説を確認しましょう。 全体像を見てみましょう。 以下の関数は時系列から時間を連続して削除し、1時間しか残しません。 このシリーズの価格差を構築し、他の時間に構築されたシリーズとの相関関係を決定します。
#calculate correlation heatmap between all hours def correlation_heatmap(symbol, lag, corrthresh): out = pd.DataFrame() rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') for i in range(24): ratesH = None ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna() out[str(i)] = ratesH['close'].reset_index(drop=True) plt.figure(figsize=(10, 10)) corr = out.corr() # Generate a mask for the upper triangle mask = np.zeros_like(corr, dtype=np.bool) mask[np.triu_indices_from(mask)] = True sns.heatmap(corr[corr >= corrthresh], mask=mask) return out out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)
この関数は、増分オーダー (タイム ラグ) と、小さい相関で時間を降ろす相関閾値を受け入れます。 結果は次の通りです。

図4. 2015 年から 2020 年の期間の異なる時間の増分間の相関関係のヒート マップ。
次のクラスターには、最大相関が設定されているのは明らかです: 0-5時と 10 - 14時。 前回の記事では、(boxplotを使用して)別の方法で発見された最初のクラスターに基づいてトレードシステムを作成しました。 パターンがヒート マップにも表示されます。 次に、2 番目の興味深いクラスターを表示して分析します。 クラスターの要約統計は次の通りです。
out[['10','11','12','13','14']].describe()
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 | 1265.000000 |
| mean | -0.001016 | -0.001015 | -0.001005 | -0.000992 | -0.000999 |
| std | 0.024613 | 0.024640 | 0.024578 | 0.024578 | 0.024511 |
| min | -0.082850 | -0.084550 | -0.086880 | -0.087510 | -0.087350 |
| 25% | -0.014970 | -0.015160 | -0.014660 | -0.014850 | -0.014820 |
| 50% | -0.000900 | -0.000860 | -0.001210 | -0.001350 | -0.001280 |
| 75% | 0.013460 | 0.013690 | 0.013760 | 0.014030 | 0.013690 |
| max | 0.082550 | 0.082920 | 0.085830 | 0.089030 | 0.086260 |
すべてのクラスター時間のパラメータは近いが、分析されたサンプルの平均値は負 (約 100 小数点以下5桁ポイント) です。 平均増分の変化は、相場が成長するよりも時間の間に減少する可能性が高いことを示します。 また、増分ラグの増加は、トレンド成分の出現による時間間の相関が大きくなる一方で、ラグの減少は値の低下につながることも注目に値します。 ただし、クラスタの相対的な配置はほとんど変わりません。
たとえば、単一のラグの場合、時間 12、13、および 14 の増分は依然として強く相関します。
plt.figure(figsize=(10,5)) plt.plot(out[['12','13','14']]) plt.legend(out[['12','13','14']]) plt.show()
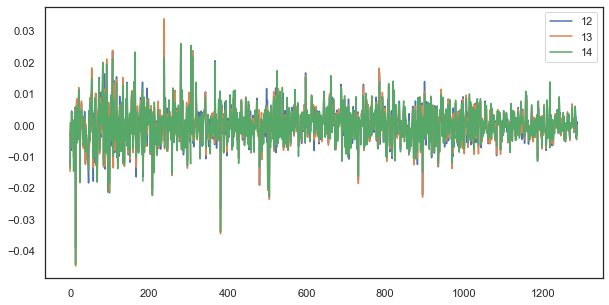
図5. 異なる時間で構成される単一のラグによる一連の増分間の視覚的類似性
ルール性の公式:シンプルだが良い
仮説を覚えておいてください:
価格増分の相関は、季節パターンの存在、および近くの増分のクラスタリングに依存します。 f
自己相関図とヒートマップでは、過去の値と近くの時間単位の両方に毎時増分の依存性があることが分かりました。 最初の現象は、一日の特定の時間にイベントの再発に由来します。 2つ目は、特定の期間におけるボラティリティのクラスタリングに関連します。 現象は、どちらも個別に考慮し、可能であれば組み合わせる必要があります。 この記事では、以前の値に対する特定の時間増分(時系列から他のすべての時間を削除)の依存性に関する追加の調査を行います。 研究の最も興味深い部分は、次の記事で行われます。
# calculate joinplot between real and predicted returns def hourly_signals_statistics(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') # price differences for every hour series H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna() H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna() # current returns for both hours HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True) # previous returns for both hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # Basic equation: ret[-1] = ret[0] - (ret[lag] - ret[lag-1]) # or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) predicted = HF-(HF2-HL2) real = HL # correlation joinplot between two series outcorr = pd.DataFrame() outcorr['Hour ' + str(hour)] = H['close'] outcorr['Hour ' + str(hour2)] = H2['close'] # real VS predicted prices out = pd.DataFrame() out['real'] = real['close'] out['predicted'] = predicted['close'] out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))] # plptting results from scipy import stats sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)
上記のリストで行われていることの説明を次に示します。 どの価格増分(その差額)が計算されるかに基づいて、不要な時間を取り除くことによって形成された2つのシリーズがあります。 シリーズの時間は"hour"と"hour2"パラメータで決定されます。 次に、毎時1時間のラグで配列を取得します。 HFシリーズは、1つの値でHLの前にある - 実際の増分と予測された増分、ならびに間の差を計算することができます。 まず、1時間目と2時間目の増分の散布図を作成してみましょう。
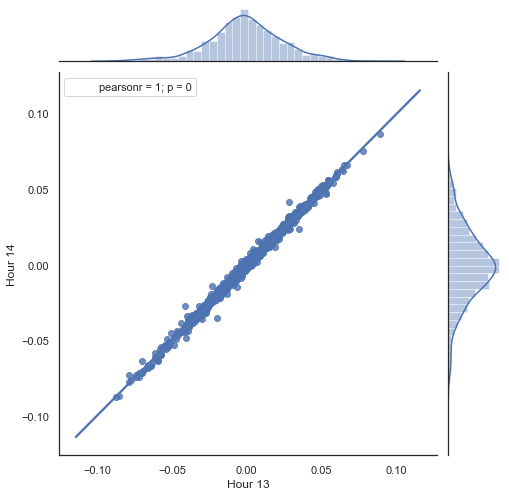
図5. 2015 年から 2020 年の13時と14時の増分の散布図
予想どおり、増分は高い相関関係にあります。 次に、前の増分に基づいて次の増分を予測してみましょう。 これを行うには、次の値を予測できる簡単な数式を次に示します。
Basic equation: ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1]))
結果の式の説明を次に示します。 未来の増分を予測するために、ゼロバーに入っています。 次の増分ret[-1] の値を予測します。 これを行うには、現在の増分から前の増分 ("lag" と"lag-1") と次の増分の差を引きます。 隣接する2時間の増分の相関が強い場合、この式で予測増分が記述されると予想できます。 以下は終値の方程式の説明です。 したがって、未来の予測は3つの増分に基づいています。 2 番目のコード部分では、未来の増分を予測し、実際の増分と比較します。 チャートは次の通りです。
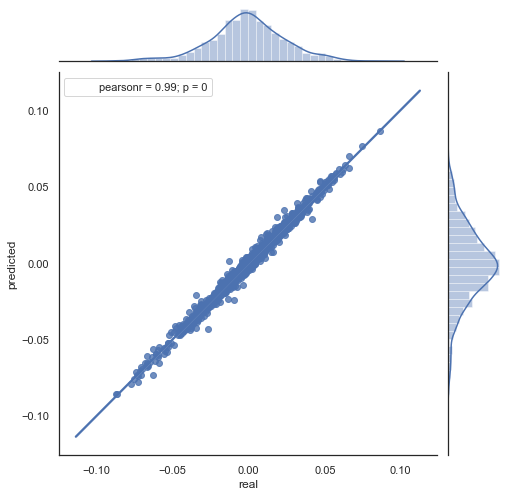
図6. 2015 年から 2020 年の期間の実績および予測増分の散布図
図5 と 図6 のチャートが似ていることがわかります。 相関を介してパターンを決定する方法が適切であることを意味します。 同時に、値はチャート全体に分散されます。同じ行に置かれていない。 予測に悪影響を及ぼす予測誤差です。 個別に処理する必要があります (この記事では説明しません)。 ゼロの周りの予測は本当に興味深いものではありません:次の価格増分の予測が現在の価格増分と等しい場合、そこから利益を生み出すことはできません。 予測は、rfilter パラメータを使用してフィルタ処理できます。
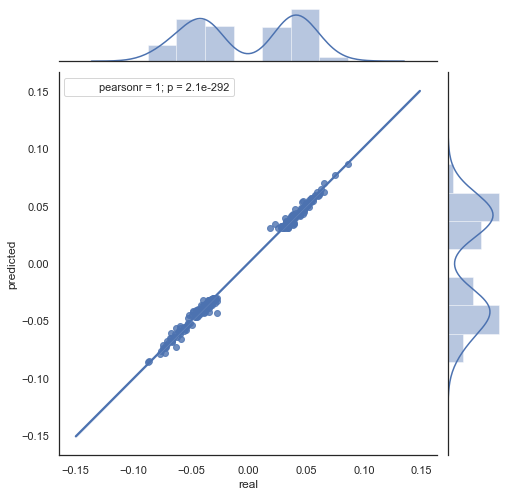
図7. 2015 年から 2020 年の期間のrfilter = 0.03 を使用した実績および予測増分の散布図
ヒート マップは、2015 年から現在の日付までのデータを使用して作成されています。 開始日を2000年に戻しましょう。
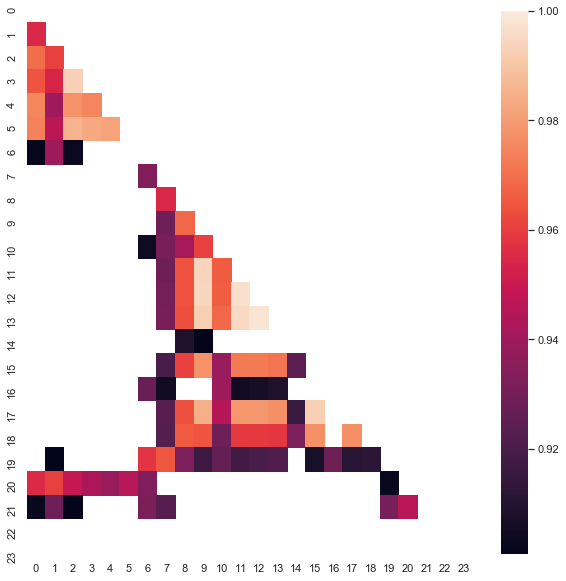
図8. 2000年から 2020 年までの期間の異なる時間の増分間の相関関係のヒート マップ。
| 10 | 11 | 12 | 13 | ||
|---|---|---|---|---|---|
| count | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 | 5151.000000 |
| mean | 0.000470 | 0.000470 | 0.000472 | 0.000472 | 0.000478 |
| std | 0.037784 | 0.037774 | 0.037732 | 0.037693 | 0.037699 |
| min | -0.221500 | -0.227600 | -0.222600 | -0.221100 | -0.216100 |
| 25% | -0.020500 | -0.020705 | -0.020800 | -0.020655 | -0.020600 |
| 50% | 0.000100 | 0.000100 | 0.000150 | 0.000100 | 0.000250 |
| 75% | 0.023500 | 0.023215 | 0.023500 | 0.023570 | 0.023420 |
| max | 0.213700 | 0.212200 | 0.210700 | 0.212600 | 0.208800 |
ご覧の通り、ヒート マップはやや薄くなり、13 時間から 14 時までの依存度は低下します。 同時に、増分の平均値は正の値で、買いの優先順位が高くなります。 平均値のシフトは、両方の時間間隔で効果的にトレードを許可しませんので、選択する必要があります。
この期間の結果の散布図を見てみましょう (ここでは、実際の予測チャートのみを提供します)。

図9. rfilter = 0.03 (期間 2000 から 2020 の) で実績および予測増分の散布図
値の広がりは増加しており、このような長期間の負の要因です。
したがって、特定の時間の実際の増分と予測された増分の分布の公式と概算のアイデアを得ています。 より明確にするために、依存関係を3Dで視覚化することができます。
# calculate joinplot between real an predicted returns def hourly_signals_statistics3D(symbol, lag, hour, hour2, rfilter): rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume']) rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') rates = pd.DataFrame(rates['close'].diff(lag)).dropna() out = pd.DataFrame(); for i in range(hour, hour2): H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None; H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True) H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True) HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True); # current hours HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True) # last day hours predicted = HF-(HF2-HL2) real = HL out3D = pd.DataFrame() out3D['real'] = real['close'] out3D['predicted'] = predicted['close'] out3D['predictedABS'] = predicted['close'].abs() out3D['hour'] = i out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))] out = out.append(out3D) import plotly.express as px fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000) fig.show() hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)
この関数は、予測値と実際の値を計算するために、既に既知の数式を使用します。 各個別の散布図は、前日の 100 増分でシグナルが生成されたかのように、各時間の実際の予測依存性を示します。 10.00 から 23.00 までの時間を例として使用します。 最も近い時間の間の相関関係は最大です。 距離が長くなるにつれて、相関が減少します(散布図は円のようになっられます)。 16時間から始まり、さらに時間は前日の時間10にほとんど依存しません。 添付を使用して、3D オブジェクトを回転してフラグメントを選択すると、より詳細な情報を取得できます。
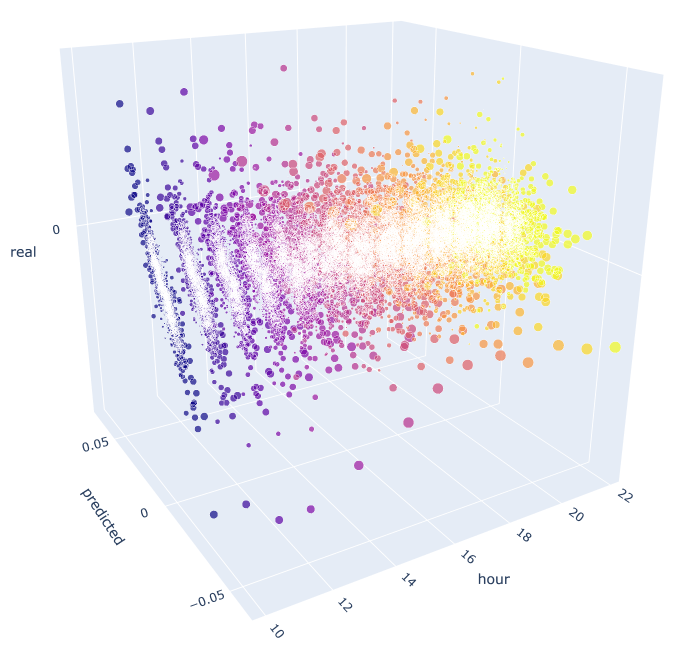
図10. 2015 年から 2020 年までの実際の増分と予測された増分の 3D 散布図
次に、EAを作成して、どのように機能するかを確認します。
識別された季節パターンをトレードするEAの例
前の記事の例と同様に、ロボットは、現在の増分と前のインクリメントとの間の統計的関係に基づく季節パターンを1時間だけトレードします。 差は、他の時間がトレードされ、提案された式に基づく原則が使用するということです。
統計的な調査に基づいて、結果の式をトレードに使用する例を考えてみましょう。
input int OpenThreshold = 30; //Open threshold input int OpenThreshold1 = 30; //Open threshold 1 input int OpenThreshold2 = 30; //Open threshold 2 input int OpenThreshold3 = 30; //Open threshold 3 input int OpenThreshold4 = 30; //Open threshold 4 input int Lag = 10; input int stoploss = 150; //Stop loss input int OrderMagic = 666; //Orders magic input double MaximumRisk=0.01; //Maximum risk input double CustomLot=0; //Custom lot
パターンを使用して次の間隔が決定されました: {10, 11, 12, 13, 14} 基づいて、"オープン閾値"パラメータは毎時間個別に設定することができます。 パラメータは、図9の"rfilter"に似ています。 「ラグ」変数には、増分のラグ値が含まれています(デフォルトでは25のラグ、つまりH1時間枠のほぼ1日を分析しました)。 時間ごとにラグを個別に設定することもできますが、ここではすべての時間に同じ値を使用して、わかりやすくします。 SLは、すべてのポジションで同じです。 パラメータはすべて最適化できます。
トレードロジックは次の通りです。
void OnTick() { //--- if(!isNewBar()) return; CopyClose(NULL, 0, 0, Lag*2+1, prArr); ArraySetAsSeries(prArr, true); const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1])); TimeToStruct(TimeCurrent(), hours); if(hours.hour >=10 && hours.hour <=14) { //if(countOrders(0)==0) // if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY)) // OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN); if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) { if(pr <= -signal && hours.hour==10) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic); if(pr <= -signal1 && hours.hour==11) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic); if(pr <= -signal2 && hours.hour==12) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic); if(pr <= -signal3 && hours.hour==13) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic); if(pr <= -signal4 && hours.hour==14) OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic); } } }
'pr' 定数は、上記の指定された数式で計算されます。 この式は、次の足で価格の増分を予測します。 その後、各時間の条件がチェックされます。 増分が特定の時間の最小閾値を満たす場合、売り取りが開始されます。 平均増分を負のゾーンにシフトすると、2015年から2020年までの間に買いが無効になることがわかりました。
図11で指定したパラメータを使用して遺伝的最適化を開始し、結果を見てみましょう:
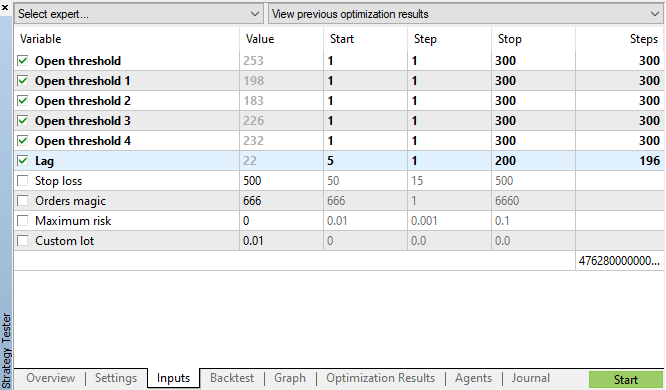
図11. 遺伝的最適化パラメータの表
最適化チャートを見てみましょう。 最適化された間隔では、最も効率的なラグ値は 17 ~ 30 時間の間に配置され、前日の同じ時間の現在の日の特定の時間の増分の依存性に関する仮定に近いです。
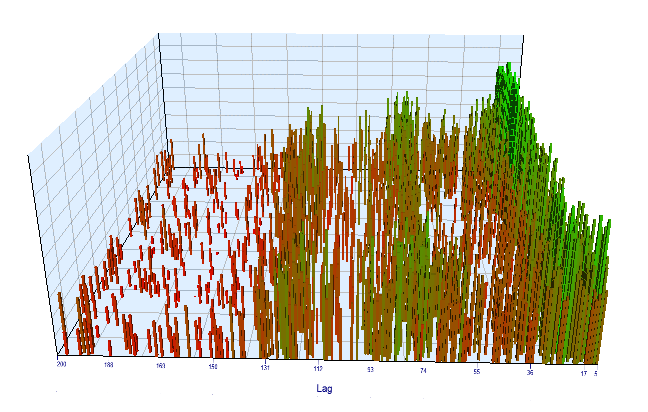
図12. 最適化された間隔で 'Order 閾値' 変数に対する 'Lag' 変数の関係
フォワードチャートも同様に表示されます。
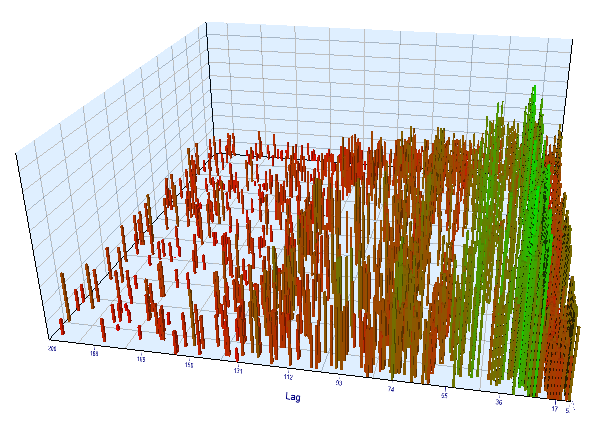
図13. 前方間隔の 'Order 閾値' 変数に対する 'Lag' 変数の関係
バックテストおよびフォワード最適化テーブルの最適な結果を次に示します。
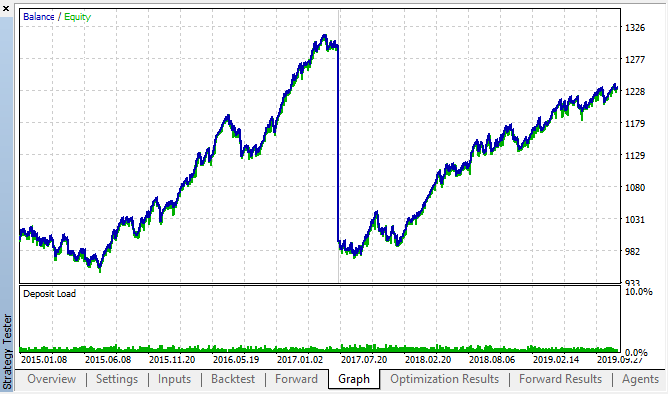
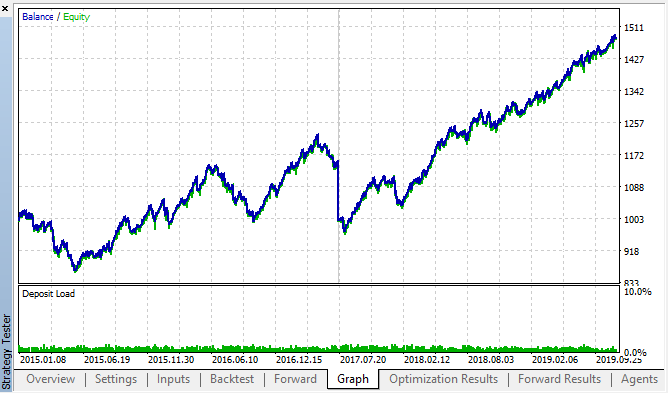
図14、図15. バックテストとフォワードの最適化チャート。
パターンは、2015 年から 2020 年の間隔全体にわたって持続することが確認できます。 計量的アプローチは完全にうまくいったと考えることができます。 一部のクラスタリングでは、次の曜日の同じ時間単位の間に依存関係があります (依存関係は同じ時間ではなく、近い時間の場合もあります)。 次の記事では、2番目のパターンの使い方を分析します。
別の時間枠で増分期間を確認する
M15時間枠に関する追加のチェックを行いましょう。 現在の時間と前日の同じ時間の間の同じ相関関係を探しているとします。 この場合、有効ラグは4倍大きく、毎時4つのM15期間が含まれているため、約24 *4 = 96でなければなりません。 同じ設定とM15時間枠でEAを最適化しました。
最適化された間隔では、結果として生じる有効なラグは <60 ですが、奇妙です。 オプティマイザが別のパターンを検出したか、EAが最適化し過ぎていた可能性があります。
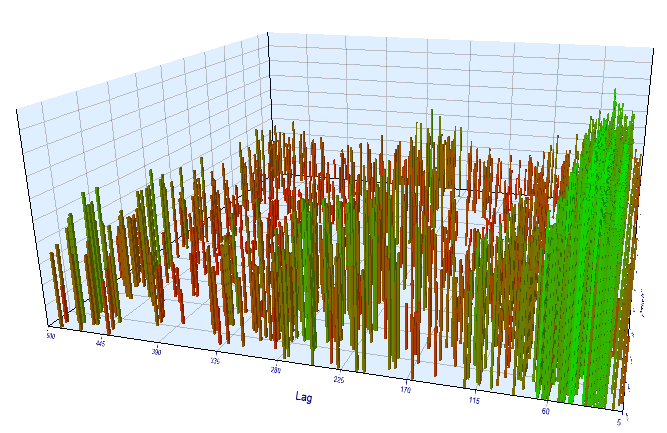
図16. 最適化された間隔で 'Order 閾値' 変数に対する 'Lag' 変数の関係
フォワードテスト結果については、遅延が正常で、パターンを確認する100に相当します。
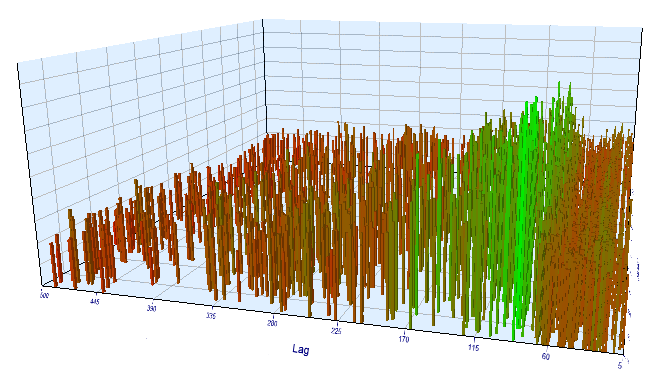
図17. 前方間隔の 'Order 閾値' 変数に対する 'Lag' 変数の関係
最適なバックテストとフォワードの結果を見てみましょう:
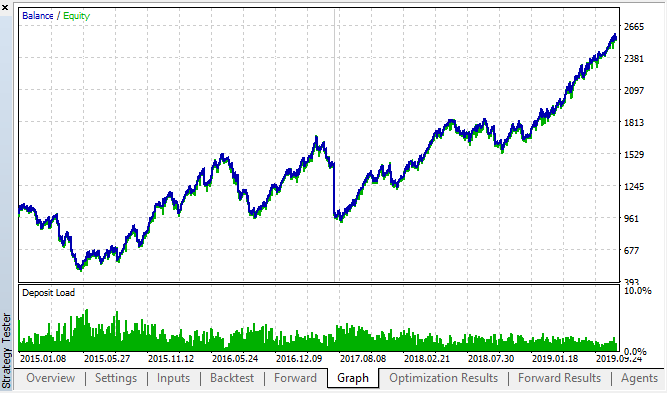
図18. バックテストとフォワード;最高のフォワードパス
結果の曲線は、トレード数が大幅に増加する H1 チャート曲線に似ています。 おそらく、戦略は、より低い時間枠に最適化することができます。
結論
この記事では、次の仮説を提唱しました。
価格増分の相関は、季節パターンの存在、および近くの増分のクラスタリングに依存します。
最初のパートは完全に確認されました。つまり、毎時の増分の間には異なる週を形成する相関関係があります。 2 番目の主張は暗黙的に確認されました。つまり、相関関係にはクラスタリングがあり、現在の時間の増分も隣接する時間の増分に依存します。
提案されたこのEAは、決して見つかった相関関係をトレードするための唯一無二のものではありません。 提案されたロジックは、相関に関する著者の見解を反映し、EAの最適化は統計調査によって見つかったパターンをさらに確認するためにのみ行われました。
研究の第2部では追加の実質的な研究を必要とするため、次の記事では簡単な機械学習モデルを使用して、仮説の第2部を完全に確認または反論します。
添付ファイルには、Jupyter ノートブック形式のすぐに使用できるフレームワークが含まれており、他の金融商品の学習に使用できます。 その結果は、添付のテストEAを使用してさらにテストすることができます。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/5451
 トレードシグナルの多通貨監視(パート1):アプリケーション構造の開発
トレードシグナルの多通貨監視(パート1):アプリケーション構造の開発
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索