マキシム、よくやった!
質問はこうだ。私の理解は正しいでしょうか?
は本質的に偏自己相関関数(PACF)なのでしょうか?
ありがとうございます。
この記事は、それ自体として、またトレーディング記事のあるべき姿の例として、良いものである。
欠点は、著者の前回の記事と同様、プラスの収益性の重要性を評価していないことである。有意性が低ければ、取引する前に戦略を改良する必要がある。この記事のTSの場合、一見したところ、有意性は取引回数とシャープレシオからおおよそ推定できる。
この記事はそれ自体として、またトレーディング記事のあるべき姿の見本として良いものだ。
欠点は、著者の前回の記事と同様、プラスの収益性の重要性を評価していないことである。有意性が低ければ、取引する前に戦略を改良する必要がある。この記事のTSの場合、一見したところ、有意性は取引回数とシャープレシオからおおよそ推定できる。
ありがとうございます。詳細な検証や有意性評価については、このトピック全体が出尽くしたときに追加すればよい。つまり、これは最適な取引アルゴリズムではなく、オプティマイザーを通じていくつかの規則性を追加的にチェックするだけだと思います。
モード切り替えの問題はまだ解決されていないが、これはこのトピックの論理的な続きと思われる。そうでなければ、すべての推定は特定の市場モード(この場合は過去5年間)に対して行われることになり、これは間違っています。
Видно, что закономерность сохраняется на всем интервале 2015-2020гг. Можно считать, что наш эконометрический подход сработал на отлично.
もし、「パターン・サーチ」が行われたのと同じエリアで、最適化が悪い結果を示したとしたら、おかしいだろう?
もし、「パターン・サーチ」が行われたのと同じエリアで、最適化が悪い結果を示したとしたら、おかしいだろう?
もし、異なるラグを示したとしたら、その研究は間違っていたことになる。ただのテストだ。
もし彼女が別の遅れを示したなら、その研究は間違っていることになる。念のため。
マキシム
私の質問に答えてください
https://www.mql5.com/en/forum/219788/page2#comment_15129306
ありがとうございました。

- 2017.11.21
- www.mql5.com
ご挨拶を申し上げます、
ありがとうございました。この記事はとても洞察に富んでいて役に立ちました。
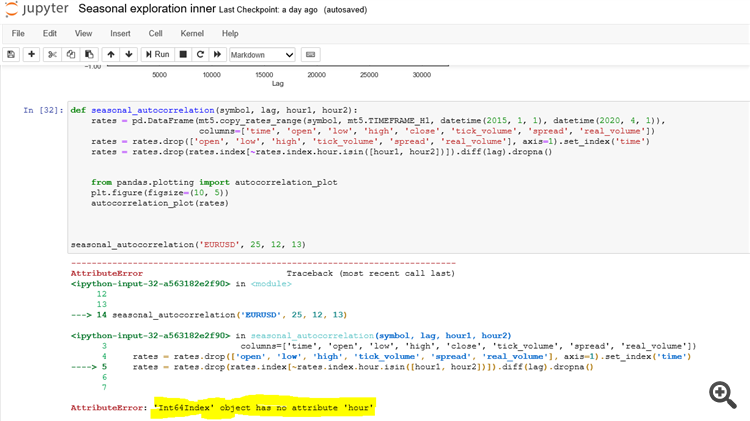
私はjupyter Notebookであなたのコードを実践しようとしたときにエラーに直面しました、
---------------------------------------------------------------------------AttributeError Traceback (most recent call last)<ipython-input-32-a563182e2f90> in<module> 12 13 --->14 seasonal_autocorrelation('EURUSD',25, 12,13) <ipython-input-32-a563182e2f90> inseasonal_autocorrelation(symbol, lag, hour1, hour2) 3 columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])) 4 rates= rates. drop(['open','low', 'high','tick_volume', 'spread','real_volume'], axis=1). set_index('time')----> 5 rates= rates. drop( rates. index[~rates. index. hour. isin([ hour1, hour2])]). diff( lag). dropna() 6 7 AttributeError: 'Int64Index' オブジェクトには 'hour' という属性がありません。
ご挨拶
ありがとうございました。この記事はとても洞察に富み、参考になりました。
私はjupyter Notebookであなたのコードを実践しようとしてエラーに直面しました(あなたのサポートファイルに本当に感謝します)、
------------------------------------------------------------------------------------------------AttributeError Traceback (most recent call last)<ipython-input-32-a563182e2f90> in<module> 12 13 --->14 seasonal_autocorrelation('EURUSD',25,12,13)<ipython-input-32-a563182e2f90> inseasonal_autocorrelation(symbol, lag, hour1, hour2) 3 columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])) 4 rates= rates. drop(['open','low','high','tick_volume','spread','real_volume'], axis=1). set_index('time')----> 5 rates= rates. drop( rates. index[~rates. index. hour. isin([ hour1, hour2])]). diff( lag). dropna() 6 7 AttributeError: 'Int64Index' オブジェクトには属性 'hour' がありません。
こんにちは、MetaQuotesはpython APIを変更しました。後で修正して新しいノートブックを添付します。
また、このサイトで新しいドキュメントを確認できます。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事 相場パターンを見つけるための計量的アプローチ:自己相関、ヒートマップ、散布図 はパブリッシュされました:
この記事では、季節的特徴の拡張である自己相関ヒートマップと散布図を紹介します。 この記事の目的は、"マーケットメモリ"が季節的な性質を持ち、任意のオーダーの増分の最大相関によって表現されることを示すものです。
M15時間枠に関する追加のチェックを行いましょう。 現在の時間と前日の同じ時間の間の同じ相関関係を探しているとします。 この場合、有効ラグは4倍大きく、毎時4つのM15期間が含まれているため、約24 *4 = 96でなければなりません。 同じ設定とM15時間枠でEAを最適化しました。
最適化された間隔では、結果として生じる有効なラグは <60 ですが、奇妙です。 オプティマイザが別のパターンを検出したか、EAが最適化し過ぎていた可能性があります。
図16. 最適化された間隔で 'Order 閾値' 変数に対する 'Lag' 変数の関係
フォワードテスト結果については、遅延が正常で、パターンを確認する100に相当します。
図17. 前方間隔の 'Order 閾値' 変数に対する 'Lag' 変数の関係
作者: Maxim Dmitrievsky