El modelo de regresión de Sultonov (SRM): pretende ser un modelo matemático del mercado.
búsqueda de patrones, descripción de los principales patrones
Todos los supuestos básicos de la teoría de la correlación y la regresión se basan en la suposición de que los datos estudiados se distribuyen normalmente. ¿Tienen sus insumos (precios) una distribución normal?
Todos los supuestos básicos de la teoría de la correlación y la regresión se basan en la suposición de que los datos estudiados se distribuyen normalmente. ¿Tienen sus insumos (precios) una distribución normal?
no lo consiguió
En principio, demostraré que el RMS detecta cualquier patrón incrustado en una serie de dígitos, incluidas las series temporales (RT), creo, independientemente de la naturaleza de la aparición de esos dígitos en la serie. Todas estas y otras sutilezas se discutirán con ejemplos concretos, incluyendo el análisis de series aleatorias.
El RMS encontrará un patrón válido o ficticio, pero debido a la falta de normalidad de la distribución el valor predictivo del modelo será 0. Esto no son sutilezas, esto es el fundamento.
¿Qué es exactamente lo que no has entendido?
RMS encontrará un patrón real o imaginario, pero debido a la falta de normalidad de la distribución, el valor predictivo del modelo será 0. Esto no es una sutileza, es el fundamento.
RMS encontrará la dependencia más adecuada, en lugar de una dependencia derivada. Y sobre la ausencia o presencia de la normalidad de la distribución de los datos iniciales vamos a abrir una discusión separada y dejar que los expertos de esta base hablen aquí en paralelo.
Lo tengo..... Y claro, olvídalo, ¡normalidad! Simplemente se interpone en el camino.
P.D. el valor predictivo del modelo será cercano a 0
Empecemos con una función lineal.
Imaginemos que la serie viene dada por los números Yi = a+bxi:
xi Yi
0,00000001 10,0000
1,00000001 15,0000
2,00000001 20,0000
3,00000001 25,0000
4,00000001 30,0000
5,00000001 35,0000
6,00000001 40,0000
7,00000001 45,0000
8,00000001 50,0000
9,00000001 55,0000
10,00000001 60,0000
11,00000001 65,0000
12,00000001 70,0000
13,00000001 75,0000
14,00000001 80,0000
15,00000001 85,0000
16,00000001 90,0000
17,00000001 95,0000
18,00000001 100,0000
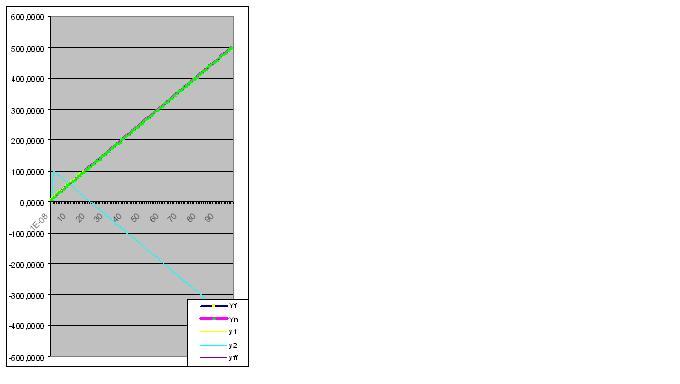
Aquí hay un gráfico de los valores reales y calculados, el error del modelo es de 2,78163E-14%:
Lo tengo..... Y con razón: ¡al diablo con la normalidad! Sólo estorba.
P.D. el valor predictivo del modelo será cercano a 0
Debido a su persistencia, tengo que empezar por demostrar la capacidad de predicción del modelo analizando la función Y=tg(0,1x)+2 e introduciendo los 8 primeros pares de dígitos:
xi Yi
0,00000001 2,0000
1,00000001 2,1003
2,00000001 2,2027
3,00000001 2,3093
4,00000001 2,4228
5,00000001 2,5463
6,00000001 2,6841
7,00000001 2,8423
Error 0,427140953%:
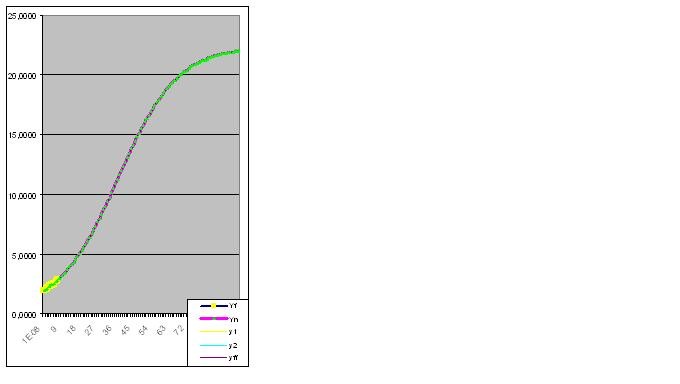
Sin embargo, una vez introducido el noveno par de dígitos, el modelo predice inmediatamente el comportamiento "extraño" del objeto en el futuro:
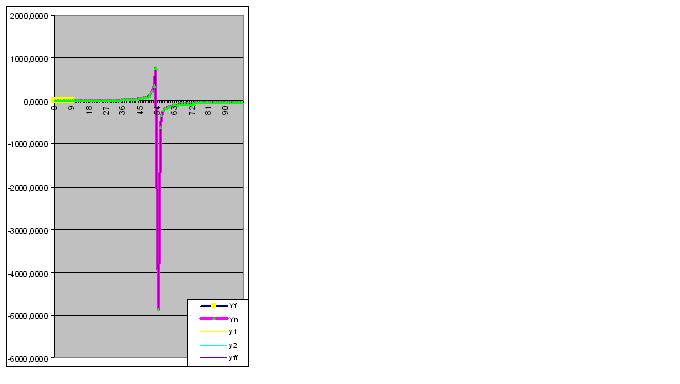
La introducción de más datos acerca la "anomalía" prevista a los datos originales:
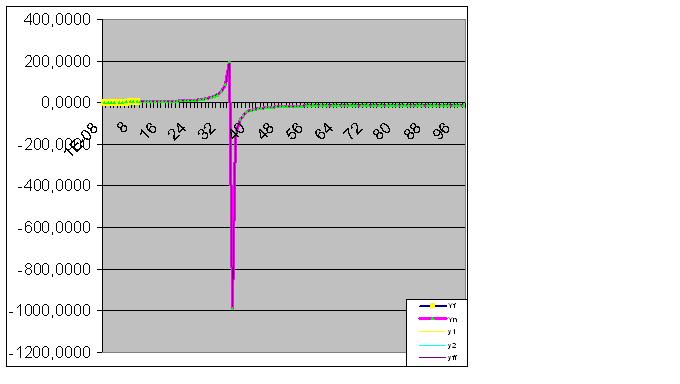
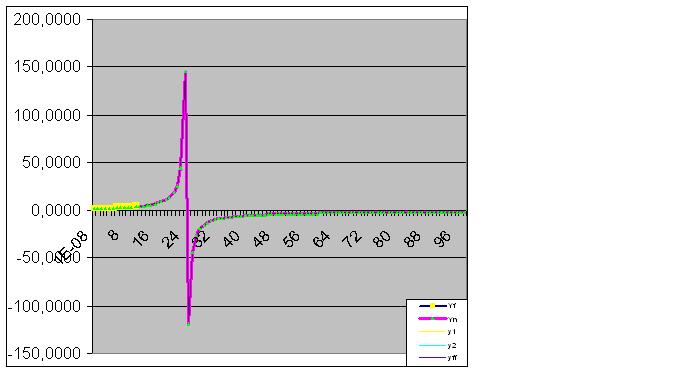
Aquí los datos brutos también han comenzado a realizar la "finta" prevista:
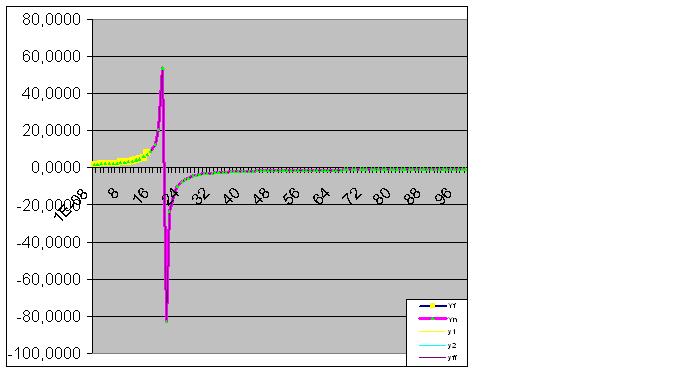
Finalmente, la predicción se cumple perfectamente:
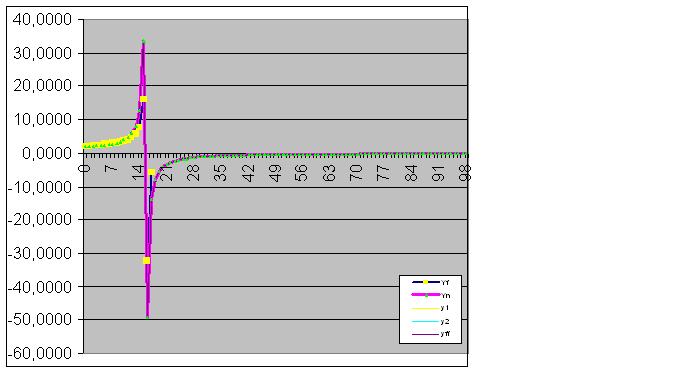
A continuación, el modelo capta perfectamente el estado final del objeto, de modo que la suma de los valores reales de la función es igual a la RMS calculada con precisión informática
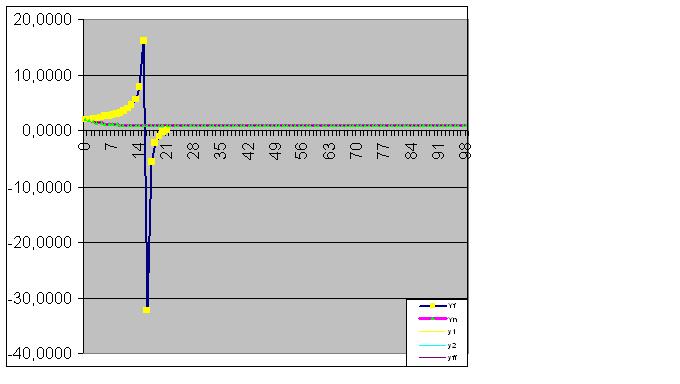
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Estimados miembros del foro, no es ningún secreto que la cuestión de encontrar las dependencias que describen los patrones básicos del mercado es importante. Aquí trataremos de abordar esta cuestión con todos los medios de análisis disponibles, incluyendo diversas propuestas de los participantes en esta materia y el material teórico y práctico acumulado hasta el momento de todas las fuentes posibles. Como resultado de este trabajo, si nos detenemos aunque sea en una visión de esta función, creo que consideraremos que el tiempo y el esfuerzo no se han gastado en vano.
Comenzaré demostrando las capacidades de RMS con ejemplos sencillos de descripciones de patrones conocidos: lineal, parábola, hipérbola, exponente, seno, coseno, tangente, cotangente y otros, así como su combinación, que ciertamente están presentes en el mercado. Le ruego que me apoye en este impulso con sugerencias constructivas y críticas sanas si es necesario.