Diskussion zum Artikel "Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal"
Wenn es möglich ist, bitte ich den Autor dieses Artikels, die folgenden Argumente zu berücksichtigen:
Bisher habe ich gesehen, dass das Prinzip des Goldenen Schnitts verwendet werden kann, um fraktal-probabilistische Ketten zu konstruieren, die eine vollständige Gruppe von Ereignissen bilden, aber ich sehe ehrlich gesagt nicht, was ein solcher Ansatz bringen kann. Es scheint, dass der Goldene Schnitt auch mit Fibo-Reihen verbunden ist, aber auch hier sehe ich nicht, wie er angewendet werden kann und wofür, wenn Sie Ideen haben, die Sie hier schreiben können, denke ich, dass es hier ein Plus wäre. Und so im Allgemeinen haben sich diese Prozesse bereits in meinem Kopf gebildet, im Allgemeinen ist das alles, was nötig ist, um komplexere Formeln abzuleiten. Bis jetzt erfüllen die gewonnenen Fraktale ihre Aufgabe. Da geht alles von komplex zu einfach und so weiter. Ich kann über die Anwendung des Goldenen Schnitts nachdenken, aber ich kann nicht erkennen, wie er nützlich sein soll. Auch Fibo-Reihen, jeder sagt Fibo-Fibo ... Ololo, sie hören ein kluges Wort und wiederholen es wie ein Papagei. Ich gehe immer davon aus, dass ein mathematisches Prinzip einem bestimmten Problem entspricht, und finde nach einiger Zeit immer eine Lösung für jedes Problem. Das Werkzeug der Lösung wird dabei ausgewählt, das Gehirn selbst findet es, und wenn möglich findet es Ähnlichkeiten mit etwas, das man im Ohr hat. Mit anderen Worten, zuerst bestimmen wir, was wir finden müssen, und dann suchen wir nach Möglichkeiten, das Problem zu lösen. Ich wäre mehr daran interessiert, spezifische Probleme zu hören, und Sie können einen separaten Artikel mit solchen Lösungen machen, es wäre interessant und würde Spaß machen, denke ich. Im Rahmen dieser Probleme können wir den Goldenen Schnitt und alles andere anwenden, solange das Ergebnis wirklich gebraucht wird und jemandem einen konkreten Nutzen bringt. Sie können also Vorschläge schreiben.
Wenn es möglich ist, bitte ich den Autor dieses Artikels, die folgenden Argumente zu berücksichtigen:
Dies ist nur ein abgedroschener Mythos von angeblichen Fibo und ZS überall....
Das Lustige ist, dass man, wenn man irgendeinen Topf nimmt und ihn gut verdreht, sowohl Fibo als auch Goldener Schnitt und Pi und e und viele andere Dinge darin finden kann....
Es ist nur ein abgedroschener Mythos von angeblich Fibo und ZS überall und überall...
Das Lustige ist, dass wenn man jeden Topf nimmt und ihn gut dreht, man darin den Fibo und den Goldenen Schnitt und die Zahl von Pi und die Zahl von e und viele andere Dinge finden kann....
Fibas (sie sind auch der Goldene Schnitt, was viele Menschen nicht wissen) werden extrem leicht gesucht, d.h. gesehen. Denn sie sind Exponentiale. Die wiederum Summen sind...Im Allgemeinen kann man sehr lange Zeit elementare Dinge aus der Schule (!!!) erzählen, aber es ist nutzlos.
Man kann es auch so machen:
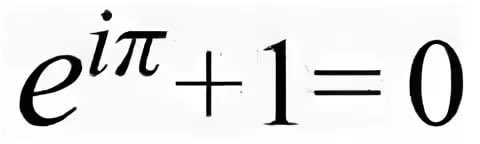
schön, geheimnisvoll...die Verbindung von FIBO mit Fourier...die Weltkonstanten in einem Glas...und anderes Zeug.
Es ist nur ein abgedroschener Mythos von angeblich Fibo und ZS überall und überall...
Das Lustige ist, dass wenn man jeden Topf nimmt und ihn gut dreht, man darin den Fibo und den Goldenen Schnitt und die Zahl von Pi und die Zahl von e und viele andere Dinge finden kann....
man kann auch Kopf und Schultern in dem Topf finden, wenn man ihn auf den Kopf stellt).
Es ist nur ein abgedroschener Mythos, dass Fibo und ZS überall sind und überall....
Das Lustige ist, dass man in jedem Topf, den man dreht und wendet, Fibo und Goldener Schnitt und Pi und E und viele andere Dinge finden kann....
Ich könnte nicht mehr zustimmen )) es ist wirklich wahr. Händler suchen sehr gerne nach einer versteckten Bedeutung, wo es gar keine gibt ). Ich versuche, den Menschen dasselbe vorsichtig zu vermitteln, aber ich weiß nicht, wie ich es tun soll, ohne die Wahrheit zu sagen, und die Wahrheit ist grausam.) Ich bin zu dem Schluss gekommen, dass es ein Problem und eine Reihe von möglichen Lösungen gibt, und alles andere ist Zeitverschwendung. Um eine Lösung zu finden, muss man zunächst das Problem klar umreißen und zumindest eine oberflächliche Vorstellung von den möglichen Wegen zu seiner Lösung haben, wenn es keine solchen Wege gibt, dann beginnt das, was oben stand, Fibonacci, Eulers Formeln und anderer sehr schöner, aber so viel nutzloser Müll, dass man unwillkürlich beginnt, zwischen den Zeilen zu lesen. Jedes Werkzeug hat seine eigene Aufgabe. In diesem Zusammenhang schlage ich vor, zu den Besonderheiten (den konkreten Aufgaben) überzugehen.
Bisher sehe ich, dass das Prinzip des Goldenen Schnitts verwendet werden kann, um fraktale Wahrscheinlichkeitsketten zu konstruieren, die eine vollständige Gruppe von Ereignissen bilden, aber ich sehe ehrlich gesagt nicht, was dieser Ansatz bewirken kann. Es scheint, dass der Goldene Schnitt auch mit Fibo-Reihen verbunden ist, aber auch hier sehe ich nicht, wie er angewendet werden kann und wofür, wenn Sie Ideen haben, die Sie hier schreiben können, denke ich, dass es hier ein Plus wäre. Und so im Allgemeinen haben sich diese Prozesse bereits in meinem Kopf gebildet, im Allgemeinen ist das alles, was nötig ist, um komplexere Formeln abzuleiten. Bis jetzt erfüllen die gewonnenen Fraktale ihre Aufgabe. Da geht alles von komplex zu einfach und so weiter. Ich kann über die Anwendung des Goldenen Schnitts nachdenken, aber ich kann nicht erkennen, wie er nützlich sein soll. Auch Fibo-Reihen, jeder sagt Fibo-Fibo ... Ololo, sie hören ein kluges Wort und wiederholen es wie ein Papagei. Ich gehe immer davon aus, dass ein mathematisches Prinzip einem bestimmten Problem entspricht, und finde nach einiger Zeit immer eine Lösung für jedes Problem. Das Werkzeug der Lösung wird dabei ausgewählt, das Gehirn selbst findet es, und wenn möglich findet es Ähnlichkeiten mit etwas, das man im Ohr hat. Mit anderen Worten, zuerst bestimmen wir, was wir finden müssen, und dann suchen wir nach Möglichkeiten, das Problem zu lösen. Ich wäre mehr daran interessiert, spezifische Probleme zu hören, und Sie können einen separaten Artikel mit solchen Lösungen machen, es wäre interessant und würde Spaß machen, denke ich. Im Rahmen dieser Probleme können wir den Goldenen Schnitt und alles andere anwenden, solange das Ergebnis wirklich notwendig ist und jemandem einen konkreten Nutzen bringt. Sie können also Vorschläge schreiben.
1. Vielleicht hat jeder schon einmal von diesem "Ololo" gehört, aber ich habe nicht über Fibo geschrieben, weil ich nicht dazu rate, Fibo-Stufen zu "ziehen", obwohl sie, wenn sie richtig berechnet werden, verwendet werden können, aber in Kombination mit Elliott-Wellen.
Natürlich ist das noch nicht alles, Sie merken, wie zeitaufwendig und mühsam diese Arbeit ist, aber ich habe diesen Thread nicht ohne Grund gestartet. Ich werde versuchen, alles zu tun, was von mir abhängt, und im Allgemeinen sollten solche Fragen, um ehrlich zu sein, von einem ganzen Team von Mathematikern und Programmierern bearbeitet werden, wenn nicht sogar von einem ganzen Institut. Was kann eine Person dagegen tun? Selbst wenn man ein Superhirn hat, gibt es so viele Daten zu verarbeiten, dass man verrückt werden kann. Ich versuche, die Aufgaben so zu stellen, dass sie meiner Zeit und meinen Fähigkeiten entsprechen; ja, ich kann mehr tun, aber das hängt jetzt nicht von mir ab. Zeit ist die wertvollste Ressource. Wenn es Leute gäbe, die an komplexen Analysen und kompletter Hingabe interessiert sind, würde ich das gerne tun. Nichtsdestotrotz wird der Zweig weitergehen und ich werde das Material abdecken, das ich kann, ich versuche immer, etwas Neues zu erzählen, soweit ich kann.
Der Mythos von der Allgemeingültigkeit des Goldenen Schnitts in der Natur ist so sehr gewachsen, dass sich die Menschen nicht einmal mit echten Prüfungen befassen und dem Charme der Schönheit der Idee des Verhältnisses zwischen dem Ganzen und seinen Teilen erliegen, aber in Wirklichkeit ist es nicht so:
- Muschelschalen von Nautilus (die gewöhnlich in Artikeln über die Magie des WD abgebildet werden) entsprechen entgegen der landläufigen Meinung nicht dem WD.
- Die Proportionen eines menschlichen Körpers aus der berühmten Zeichnung "Vitruvianischer Mensch" von Leonardo Da Vinci entsprechen nicht den realen Menschen.
- Parthenon, Pyramiden und andere Objekte entsprechen sehr ungenau der RS (gezeichnet von Mystikliebhabern).
- Objektive psychologische Untersuchungen mit dem Ziel, herauszufinden, ob der EQ die Grundlage der Wahrnehmung von Schönheit ist, sind erfolgreich gescheitert.
- Schließlich zeigen auch die quantitativen Tests der Aufschlüsselung/Ablehnung von Ebenen im Handel nicht, dass der EQ etwas besonders Wichtiges ist.
Der einzige Grund, warum die Märkte manchmal (Stichwort NUR ein einziges Mal) Fibo-Levels gut durchbrechen können, ist der kollektive Glaube einer großen Anzahl technischer Händler an Fibo-Levels (eine sich selbst erfüllende Prophezeiung), wenn sie ihre Stopps/Limits kollektiv dort platzieren, aber selbst das wird wahrscheinlich nicht funktionieren, weil die professionellen Teilnehmer, die großen institutionellen Akteure, auf einer anderen Grundlage handeln werden, und der Zusammenbruch/die Umkehrung des Fibo-Levels mag zufällig sein, aber für die EQ-Gläubigen wird es sicherlich eine Bestätigung ihres Glaubens sein.
Keith Devlin, Professor für Mathematik an der Stanford University, erklärt es einfach: "..... Die meisten Menschen haben keine Ahnung von Mathematik und können nicht einmal verstehen, wie eine Formel wie der Goldene Schnitt auf ein komplexes System angewendet werden kann, also können sie sich auch nicht selbst testen. Die Menschen glauben, den Goldenen Schnitt überall zu sehen, in der Natur und in ihren Lieblingsobjekten, aber sie können ihn nicht beweisen. Sie sind Opfer ihres natürlichen Wunsches, einen Sinn in den verschiedenen Objekten des Universums zu finden, aber aufgrund ihrer mangelnden mathematischen Kenntnisse können sie nicht erkennen, dass die Muster, die sie entdecken, illusorisch sind."
Die Menschen programmieren sich selbst (Zombie) auf die Suche nach einer einfachen Erklärung und bemühen sich, diesen Glauben aufrechtzuerhalten, das ist das Wesen des religiösen Denkens, auch im Handel...
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Kombinatorik und Wahrscheinlichkeitsrechnung für den Handel (Teil II): Das universelle Fraktal :
In diesem Artikel werden wir das Studium der Fraktale fortsetzen und besonderes Augenmerk auf die Zusammenfassung des gesamten Materials legen. Zu diesem Zweck werde ich versuchen, alle früheren Entwicklungen in eine kompakte Form zu bringen, die für die praktische Anwendung im Handel geeignet und verständlich ist.
Verwenden wir die Konstruktionsregeln, die wir im vorherigen Artikel abgeleitet haben, und ergänzen sie, um zu verstehen, wie ein Fraktal konstruiert wird. Außerdem habe ich einen kleinen Fehler in meinen Formeln gefunden, durch den eine Asymmetrisierung der Ränder nach oben oder unten unmöglich war. Die abgeleiteten Formeln erwiesen sich als korrekt und funktionieren daher für absolut jedes Fraktal. Eigentlich handelt es sich um eine Funktion zur Umsetzung eines beliebigen Fraktals. Alle möglichen Fraktale sind ein Spezialfall eines allgemeinen Fraktals. Wenn wir die drei oben definierten Fraktaltypen nehmen, sind die Bedingungen des allgemeinen Fraktals für die Implementierung dieser drei Spezialfälle wie folgt:
Schematisch sehen diese drei Arten von Fraktalen wie folgt aus:
Im Idealfall sollte "S" gegen Unendlich tendieren. Die folgenden Variablen wurden in meinem vorherigen Artikel noch nicht beschrieben. Ich werde hier die entsprechenden Beschreibungen geben, um ein vollständiges Bild davon zu bekommen, wie man die allgemeine Formel verwendet, um die Spezialfälle zu erhalten. Das Fraktal ist eine Funktion, die nach dem Prinzip einer Kettenreaktion funktioniert, wie bei einer Atombombe. Wenn die eingestellte Kettenreaktion zu tief ist, kann der Computer mit solch massiven Berechnungen überfordert sein. Wenn der Fall nicht besonders kritisch ist, wird er einfach sehr lange rechnen — Minuten, Stunden oder sogar Tage.
Autor: Evgeniy Ilin