
Wie man nicht hinterherhinkende digitale Filter erzeugt
Einleitung
Dieser Beitrag beschreibt einen der Ansätze zur Bestimmung eines nützlichen Signals (Trend) in Datenströmen. Kleine filternde (glättende) Tests, die auf Marktnotierungen angewendet werden, belegen das Potential zur Erzeugung nicht hinterherhinkender digitaler Filter (Indikatoren), die auf den letzten Bars nicht erneut gezeichnet werden.
Standardansatz
Dieser Ansatz beruht auf den klassischen Methoden zur Glättung von Zeitreihen. Mit diesem Thema beschäftigen sich viele Beiträge, die sowohl auf dieser, als auch auf anderen Websites zu finden sind. Die Ergebnisse sind auch klassisch:
- Die Änderungen in den Trends werden mit Wartezeit angezeigt;
- Eine bessere Indikatorreaktion (digitale Filter) wird erreicht, wenn man eine Abnahme der Glättungsqualität in Kauf nimmt;
- Versuche, nicht hinterherhinkende Indikatoren zu implementieren, führen zu einer Neuzeichnung auf den letzten Stichproben (Bars).
Und obwohl Händler inzwischen gelernt haben, mit diesen Dingen unter Verwendung der Beharrlichkeit ökonomischer Prozesse und anderer Tricks, zurechtzukommen, ist dies für eine Bewertung experimenteller Echtzeit-Daten wie z.B. beim Testen von Aerostructures, absolut inakzeptabel.
Das Hauptproblem
Es ist allgemein bekannt, dass der Großteil von Handelssystemen im Lauf der Zeit keine Leistung mehr zeigt und dass die Indikatoren ihre hinweisende Funktion nur über bestimmte Intervalle besitzen. Dies kann leicht erklärt werden: Marktnotierungen sind nicht stationär. Eine Definition eines stationären Prozesses steht in Wikipedia:
Anhand dieser Definition ist klar, dass Analysemethoden stationärer Zeitreihen in der technischen Analyse nicht anwendbar sind. Und das ist auch verständlich. Ein geschickter Marktmacher, der in den Markt eintritt, bringt all unsere Berechnungen, die wir zuvor im Hinblick auf die Parameter einer bekannten Reihe von Marktnotierungen gemacht haben, wieder durcheinander.
Und selbst wenn dies sonnenklar erscheint, beruhen dennoch eine Menge Indikatoren auf der Theorie der Analyse stationärer Zeitreihen. Beispiele solcher Indikatoren sind gleitende Mittelwerte und ihre Abänderungen. Es gibt jedoch auch einige Bemühungen, adaptive Indikatoren zu erzeugen. Sie sollen die "Nicht-Stationarität" von Marktnotierungen bis zu einem gewissen Maß berücksichtigen, doch anscheinend bewirken auch sie keine Wunder. Versuche, den Marktmacher zu "bestrafen", in dem man die derzeit bekannten Analysemethoden für nicht stationäre Reihen einsetzt (Wavelets, empirische Modi u.a.) sind auch nicht erfolgreich. Es sieht so aus, als würde man andauernd einen bestimmten Schlüsselfaktor übersehen oder noch gar nicht kennen.
Der Hauptgrund hierfür liegt darin, dass die verwendeten Methoden nicht für eine Arbeit mit Datenströmen ausgelegt sind. Alle (oder fast alle) Methoden wurden zur Analyse bereits bekannter oder, wenn man von technischer Analyse sprechen möchte, historischer Daten, entwickelt. Diese Methoden sind z.B. in der Geophysik bequem: man spürt das Erdbeben, holt sich das Seismogramm und analysiert das Beben dann einige Monate lang. Mit anderen Worte: all diese Methoden sind dann geeignet, wenn Unklarheiten, die im Verlauf der Filterung am Ende einer Zeitreihe auftreten, das Endergebnis beeinflussen.
Bei der Analyse von experimentellen Datenströmen oder Marktnotierungen, konzentrieren wir uns auf die jüngsten erhaltenen Daten, und nicht auf die History. Dies sind Daten, mit denen man unter Verwendung klassischer Algorithmen, nicht umgehen kann.
Cluster-Filter
Ein Cluster-Filter ist eine Reihe digitaler Filter, die sich der Anfangssequenz annähern. Man darf Cluster-Filter nicht mit Cluster-Indikatoren verwechseln.
Cluster-Filter sind sehr angenehm für die Analyse nicht stationärer Zeitreihen in Echtzeit, also kurz gesagt: Datenströme. Das bedeutet, dass diese Filter von besonderem Interesse nicht für das Glätten der bereits bekannten Zeitreihen-Werte sind, sondern um die am wahrscheinlichsten geglätteten Werte der neu erhaltenen Daten in Echtzeit zu bekommen.
Anders als verschiedene Zerlegungsmethoden oder einfach Filter mit der gewünschten Häufigkeit, erzeugen Cluster-Filter eine Zusammensetzung oder einen Fächer wahrscheinlicher Werte von Anfangsserien, die dann auf ihre Annäherung an die Anfangssequenz hin weiter analysiert werden. Die Eingabesequenz fungiert hier eher als die Referenz denn als Ziel der Analyse. Die Hauptanalyse betrifft Werte, die von einem Set an Filtern nach der Bearbeitung der erhaltenen Daten berechnet werden.
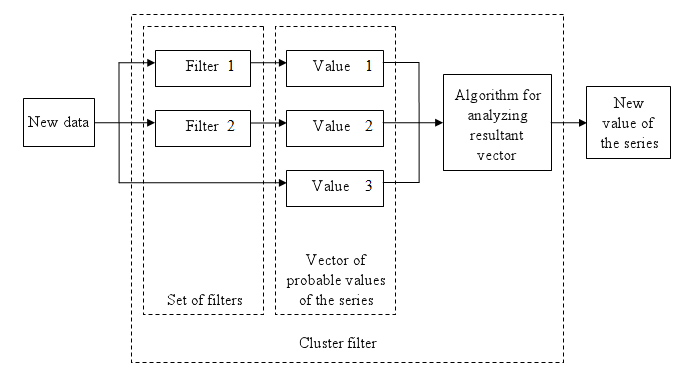
Abb. 1 Diagramm eines einfachen Cluster-Filters
Im allgemeinen Fall besitzt jeder im Cluster aufgenommene Filter seine eigenen Merkmale und steht mit keinem anderen Filter irgendwie in Bezug. Diese Filter werden manchmal zur Analyse einer stationären Zeitreihe ihrer selbst angepasst, die die einzelnen Eigenschaften der anfänglich nicht-stationären Zeitreihe beschreibt. Im einfachsten Fall "schalten" die Filter "um", wenn die anfänglich nicht-stationären Zeitreihe ihre Parameter ändert. Daher nachverfolgt ein Cluster-Filter Echtzeit-Änderungen der Merkmale.
Cluster-Filter Konzeption
Jeder Cluster-Filter kann mit folgenden drei Schritten konzipiert werden:
1. Der erste Schritt ist meist der schwierigste, doch hier werden die Wahrscheinlichkeitsmodelle der erhaltenen Datenströme gebildet. Die Anzahl dieser Modelle kann beliebig groß sein. Sie hängen nicht immer mit physischen Prozessen zusammen, die sich auf die approximierbaren Daten auswirken. Je präziser Modelle die approximierbare Sequenz beschreiben, umso größer ist die Wahrscheinlichkeit einen nicht hinterherhinkenden Cluster-Filter zu erhalten.
2. Im zweiten Schritt werden für jedes Modell ein oder mehrere digitale Filter erzeugt. Die allgemeinste Bedingung für ein Zusammenführen der Filter in ein Cluster ist, dass sie zu den Modellen gehören, die die approximierbare Sequenz beschreiben.
3. Also können wir einen oder mehrere Filter in einem Cluster haben. Und mit jeder neuen Stichprobe erhalten wir dann konsequenterweise ihren wert und einen oder mehrere Filterwerte. Also haben wir mit jeder Stichprobe einen Vektor oder künstliches Rauschen, das aus mehreren werten besteht (mindestens zwei). Jetzt müssen wir nur noch den am besten geeigneten Wert auswählen.
Beispiel eines einfachen Cluster-Filters
Zur Veranschaulichung implementieren wir einen einfachen Cluster-Filter, der dem oben stehenden Diagramm entspricht und verwenden dabei Marktnotierungen als Eingabesequenz. Dazu können Sie einfach die Abschlusskurse auf jedem Zeitrahmen hernehmen.
1. Modellbeschreibung. Wir gehen von der Voraussetzung aus, dass:
- die approximierbare Sequenz nicht-stationär ist d.h. ihre Merkmale werden sich im Laufe der Zeit verändern.
- der Abschlusskurs eines Bars nicht der aktuelle Barkurs ist. Mit anderen Worten: der registrierte Abschlusskurs eines Bars ist einer der Rauschbewegungen, wie andere Kursbewegungen auf diesem Bar auch.
- Der aktuelle Kurs oder der aktuelle Wert der approximierbaren Sequenz liegt zwischen dem Abschlusskurs des aktuellen Bars und dem Abschlusskurs des vorangegangenen Bars.
- Die approximierbare Sequenz neigt dazu, ihre Richtung beizubehalten. Also: wenn sie auf dem vorangegangene Bar nach oben verlief, dann wird sie das auf dem aktuellen Bar auch tun.
2. Auswahl digitaler Filter Zur Vereinfachung nehmen wir zwei Filter her:
- Der erste ist ein einfacher gleitender Mittelwert (MA), errechnet auf Basis der letzten zwei Abschlusskurse. Meiner Meinung nach passt das gut zur dritten Annahme, die wir für unser Modell festgelegt haben.
- Da wir ja einen nicht-stationären Filter haben, versuchen wir auch einen zusätzlichen Filter zu verwenden, der uns hoffentlich die Identifikation der Änderungen der Merkmale der Zeitreihen erleichtern wird. Ich habe dazu einen exponentiellen gleitenden Mittelwert (EMA) gewählt, da mir diese Option vernünftig und ziemlich passend erschien. Nicht zuletzt wegen der Tatsache, dass ein EGA schneller ist als ein MA und daher entlang des Trends keine Verzögerungen verursachen sollte. Und zweitens reagiert er besser auf Rauschen. Der EMA wird ebenfalls auf Basis der letzten zwei Abschlusskurse errechnet.
3. Den passenden Wert für den Cluster-Filter auswählen.
Bei jeder neuen Stichprobe erhalten wir also ihren Wert (Abschlusskurs) sowie auch den Wert von MA und EMA. Der Abschlusskurs wird gemäß der für unser Modell festgelegten zweiten Annahme ignoriert. Des weiteren wählen wir den MA- oder EMA-Wert auf Basis unserer letzten Annahme - der Beibehaltung der Trendrichtung:
Bei einem Trend nach oben, d.h. CF(i-1)>CF(i-2), wählen wir eine der folgenden vier Varianten:
sind CF(i-1)<MA(i) und CF(i-1)<EMA(i), dann ist CF(i)=MIN(MA(i),EMA(i));
sind CF(i-1)<MA(i) und CF(i-1)>EMA(i), dann ist CF(i)=MA(i);
sind CF(i-1)>MA(i) und CF(i-1)<EMA(i), dann ist CF(i)=EMA(i);
sind CF(i-1)>MA(i) und CF(i-1)>EMA(i), dann ist CF(i)=MAX(MA(i),EMA(i)).
Bei einem Trend nach unten, d.h. CF(i-1)<CF(i-2), wählen wir eine der folgenden vier Varianten:
sind CF(i-1)>MA(i) und CF(i-1)>EMA(i), dann ist CF(i)=MAX(MA(i),EMA(i));
sind CF(i-1)>MA(i) und CF(i-1)<EMA(i), dann ist CF(i)=MA(i);
sind CF(i-1)<MA(i) und CF(i-1)>EMA(i), dann ist CF(i)=EMA(i);
sind CF(i-1)<MA(i) und CF(i-1)<EMA(i), dann ist CF(i)=MIN(MA(i),EMA(i)).
Wobei:
- CF(i) – der Wert des Cluster-Filters auf dem aktuellen Bar ist;
- CF(i-1) und CF(i-2) – die Werte des Cluster-Filters auf den vorangegangen Bars sind;
- MA(i) – der Wert des einfachen gleitenden Mittelwerts auf dem aktuellen Bar ist;
- EMA(i) – der Wert des exponentiellen gleitenden Mittelwerts auf dem aktuellen Bar ist;
- MIN – der Minimalwert ist;
- MAX – der Maximalwert ist;
Programm-Code und Leistung des Cluster-Filters
Der Code des Indikators mit unserem Cluster-Filter ist nicht komplexer als der Code des gleitenden Mittelwerts. Er beruht auf keinerlei Know-How oder speziellen Techniken, also muss ich ihn hier auch nicht extra erklären. Der Quellcode ist diesem Beitrag angehängt.
Sehen Sie sich einfach, ohne viel Zeit zu vergeuden, das unten angebotene Video an und beobachten die Leistung unseres Indikators:
Video 1. Leistung eines einfachen Cluster-Filters
Es mag zwar sein, dass die Konzeption des Filters eher nach Zauberei als nach einem streng mathematischen Ansatz ausgesehen hat, doch zeigt das Video klar, dass sich die Cluster-Filterlinie wesentlich angemessener verhält die einzelnen gleitenden Mittelwerte. Man kann dies besonders deutlich an den gezackten Bereichen der Anfangsserie ablesen. Wenn Sie das noch nicht ausreichend beeindruckt hat, können wir den Cluster-Filter ja noch mit JJMA vergleichen, der als einer der besten Indikatoren gilt. Das nächste Video zeigt einen "Wettstreit" zwischen JJMA und unserem Cluster-Filter im gleichen Bereich. Ich habe versucht, JJMA-Parameter so auszuwählen, dass seine Linie mit unserer Indikatorlinie maximal übereinstimmen kann.
Video 2. Einfacher Cluster-Filter vs. JJMA
Im Durchschnitt zeigt unser Filter auf jeder Zeitreihe in etwa die gleiche Leistung wie JJMA. Doch im Gegensatz zum JJMA, der bereits komplett optimiert ist, kann unser Cluster-Filter noch weiter verbessert werden.
Fortgeschrittener Glättungseffekt
Bis jetzt hat nichts darauf hingedeutet, dass Cluster-Filter eine Eingabesequenz ohne Wartezeit glätten können. Um das zu schaffen, benötigt man einen komplexeren Filter als den bisher beschriebenen.
Zur Veranschaulichung habe ich einen GDynamik-Test-Indikator entwickelt. Er enthält zwei Indikatorzeilen:
- Blaue Linie - klassische Dynamik.
- Rote Linie - klassische Dynamik, geglättet durch einen digitalen Cluster-Filter mit einem komplexeren Algorithmus.
Die Einstellungen des Indikators decken verschiedene Testoptionen ab, die speziell für diesen Beitrag vorbereitet wurden. In den nun folgenden Tests arbeiten wir mit einem relativen Dynamik, wie er von William Blau beschrieben wurde. Wenn Sie Ihre eigenen Experimente durchführen, können Sie auch andere Dynamikvarianten hernehmen - die Ergebnisse bleiben die gleichen. Eine detaillierte Beschreibung des Indikators sowie auch Anleitungen zum Download und der Arbeit mit ihm, finden Sie in der Beschreibung des Indikators.
Hinter der Verwendung der Dynamik in diesem Artikel liegt kein spezieller Grund. Die Dynamiklinie ist ziemlich von Rauschen verzerrt und daher wird die Leistung des Filters meiner Meinung nach wesentlich besser veranschaulicht. Also lassen Sie den GDynamik-Test-Indikator laufen und analysieren das Verhalten der roten im Vergleich zur blauen Linie.
Betrachten wir uns zu allererst etwas Interessantes. Zu diesem Zweck, stellen Sie den "Filter"-Parameter auf "Test Nr.1 Fortgeschritten" ein, bevor Sie den Indikator starten. Denn die Filtereinstellungen in diesem Modus verraten ziemlich oft den sog. "führenden Effekt". Beim Testen können Sie das Glätten der gesamten Anfangslinie der Dynamik nicht sehen. Der Filter hält nach Bereichen Ausschau, wo die Chance, einen führenden Effekt zu bekommen, ziemlich groß ist. Und klar - das klappt nicht immer. Doch es passiert dennoch oft genug, dass man es bemerkt.
'Das Chart unten zeigt einen der anschaulichsten Teile der Filterleistung.
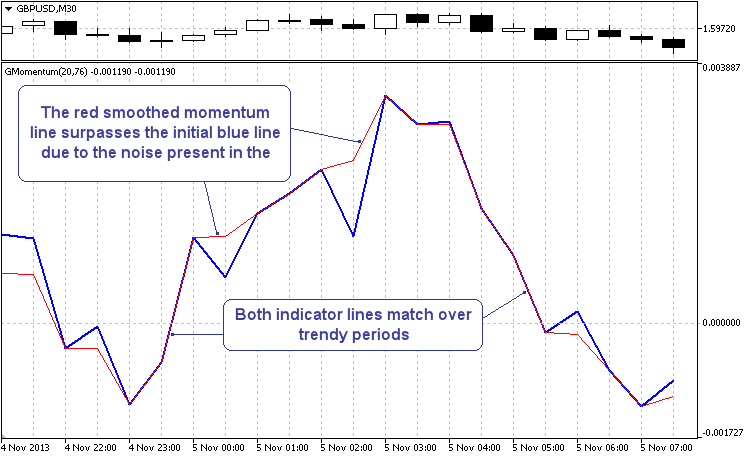
Abb. 2 Führender Effekt beim Glätten der Dynamiklinie
Es sei darauf hingewiesen, dass es nur so aussieht, als wäre es führendes Filtern. Dieser Effekt entsteht ausschließlich aufgrund der Rauschbewegungen der Dynamiklinie, und nicht so sehr weil der Filter der Zeit voraus ist. Vergleichbare Studien anderer Indikatoren (von einem einfachen MA bis zum JJMA) bestätigen, dass der führende Effekt des Glättens in jedem Indikator zu beobachten ist. Je kleiner der angegebene Zeitraum ist, umso häufiger kann dieser Effekt beobachtet werden. Jüngste Studien lassen zudem darauf schließen, dass dieser Effekt ausgeweitet werden kann. Das hängt alles von der Methode ab, mit der ein Vektor wahrscheinlicher Werte und ihrer Analyse generiert wird.
Der Kobra-Effekt
Diejenigen unter Ihnen, die den Indikator bereits in Aktion gesehen haben, könnten noch eine weitere Besonderheit feststellen. Die Indikatorlinie auf dem letzten unvollständigen Bar folgt nicht immer dem Kurs. So kann der Kurs z.B. ansteigen, doch der Indikator fällt nach - und umgekehrt. Ist der Markt schnell oder wenn man ihn im Visualizer ansieht, dann ähnelt er manchmal der Zunge einer Kobra, die eine Beute aufspürt.
Video 3. Führender Effekt beim Glätten und Kobra-Effekt
Dem-Trend-Voraus Fehler
Wir konnten oben erkennen, dass, wenn die Anfangslinie der Dynamik gegen den Trend geht (also zu rauschen beginnt), dies zum führenden Effekt der geglätteten Linie gegenüber der Anfangslinie führt. Anscheinend kann die Dynamiklinie auch eine falsche Bewegung in die andere Richtung machen, d.h. ganz unerwartet weit in Richtung des Trends hinausschießen und dort manchmal viel zu lange verweilen, selbst obwohl sich der Trend bereits umgekehrt hat. Wäre also nur logisch, wenn der Filter derartige Bewegungen verlangsamen könnte.
Sehen wir uns mal an, wie der Algorithmus diese Dem-Trend-Voraus-Fehler filtert. Zu diesem Zweck, stellen Sie den "Filter"-Parameter auf "Test Nr.2 Glätten" ein, bevor Sie den Indikator starten. Die Arbeitsweise des Cluster-Filters während dieses Tests ist in zwei Teile unterteilt.
Der kurze Indikatorname "GDynamik(Parameter 1, Parameter 2)", der im Unterfenster des Charts angezeigt wird, enthält zwei Parameter in Klammern. Ist der zweite Parameter -1, versucht der Algorithmus die Dem-Trend-Voraus Fehler zu beheben (also zu glätten). Ist der zweite Parameter größer oder = "0", werden die Einstellungen für fortgeschrittene Glättung umgesetzt.
Das unten angebotene Video zeigt die Arbeitsweise des Filters bei Veränderung seiner Empfindlichkeit vom Minimum auf den akzeptablen Wert und zurück. Um den im Video gezeigten Effekt zu bekommen, kann die Empfindlichkeit des Filter mittels der Pfeiltasten (nach unten oder oben) kontrolliert werden (vorausgesetzt, das Indikatorfenster ist aktiv).
Video 4. Filtern von Dem-Trend-Voraus-Fehler
Das obige Video lässt darauf schließen, dass, trotz der plötzlichen Kursbewegungen und der Anfangslinie der Dynamik, die Dynamiklinie während die Empfindlichkeit des Filters zunimmt, ohne Verzögerung geglättet wird. Bei maximaler Glättung, erhalten wir akzeptable Einstiegspunkte.
Nebenbei bemerkt: flache Bereiche sind für die meisten Indikator ein Problem. Denn hier werden einige Indikatoren einfach zu einer geraden Linie, selbst unter den bestehenden Einstellungen. Theoretisch gesehen kann die Technik dazu verwendet werden, jeden bestehenden Indikator zu verbessern, ohne dabei eine zusätzliche Verzögerung zu erzeugen. Für die Praxis muss das erst noch überprüft werden.
Richten Sie im nächsten Video Ihre Aufmerksamkeit darauf, wie der Filter wichtige Spitzen der anfänglichen Dynamiklinie abflacht und eine glattere Trendlinie, näher an der Kursbewegung und fast ohne Verzögerung zeichnet. Eine Erklärung warum das so ist, wird im Beitrag über die Indikatoren von William Blau geliefert.
Video 5. Glätten der Spitzen der anfänglichen Dynamiklinie.
Die beeindruckenden Ergebnisse, die man erhält, sind über die komplette History an Notierungen nicht immer die gleichen. Doch in Anbetracht der Tatsache, dass der Dynamik eine Menge Rauschen hat und der Indikator nur deswegen implementiert wurde, um eine Filterung von Datenströmen ohne Verzögerungen zu demonstrieren, können wir mit allem ziemlich zufrieden sein. Zusätzlich dazu sei darauf hingewiesen, dass der Indikator nicht neu gezeichnet wird.
Impulsantwort
Die Betrachtung der Parameter des Dynamiks mit einem eingebauten Filter erscheint ziemlich interessant. So kann die Impulsantwort z.B. gut veranschaulichen, wie und wo Spitzen von der Indikatorlinie verschwinden. Um diesen Test durchzuführen, stellen Sie den "Filter"-Parameter auf "Test Nr.3 Impuls" ein. Während des Tests erhält jeder 1024. Bar einen Einheitsimpuls. Finden Sie nachdem der Indikator läuft, die relevanten Stelle im Chart. Sie sollte so aussehen:
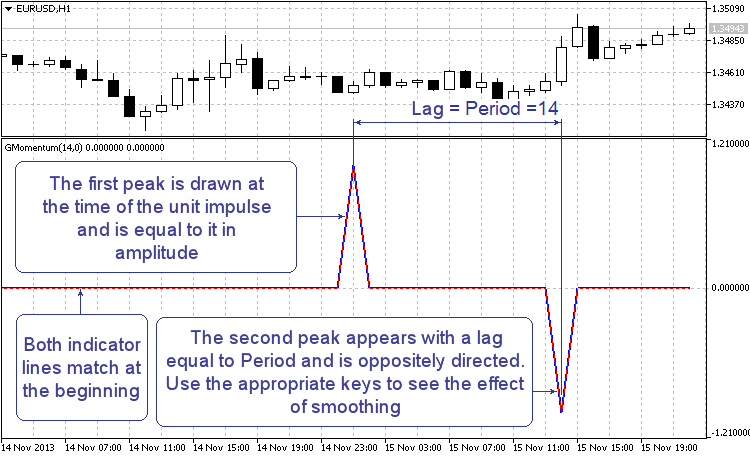
Abb. 3 Dynamikimpulsantwort
Wenn der Indikator läuft ist der Filter deaktiviert. Daher können Sie auf der blauen und der roten Linie zwei Spitzen erkennen: eine, die zum Zeitpunkt des Einheitsimpulses auftaucht und ihm gleich ist, und eine andere Spitze, die in die andere Richtung zeigt und nach der angegeben Anzahl an Zeiträumen auftaucht. So sieht die Impulsantwort der "nackten" Dynamik aus. Mit Hilfe der Pfeiletasten (nach oben oder unten) können Sie die Filterempfindlichkeit schrittweise erhöhen oder senken. Sie sollten in etwa folgendes erhalten:
Video 6. Dynamikimpulsantwort
Wie man sieht, wird die zweite Spitze vollkommen vom Filter abgeflacht, wohingegen die zweite absolut unversehrt bleibt. Der Filter bereinigt alle Dynamikeffekte und rekonstruiert exakt das Anfangsbild: ein Einheitsimpuls durch sich selbst. Verzögerungen gibt es auch keine. Und auch die Amplitude oder die Form des Einheitsimpulses werden nicht verzerrt. Sollte das der perfekte Filter in Aktion sein?
Der perfekte Filter
Es gibt einen wesentlichen Faktor, weswegen wir den hier betrachteten Filter jedoch nicht als perfekt bezeichnen können. Darauf kommen wir gleich zu sprechen.
Man nimmt an, dass es den perfekten Filter nicht gibt und dass alle Filter (Indikatoren) hinterherhinken. Doch wie erklären wir uns dann die erhaltenen Ergebnisse? Sie alle sind ja vorhanden, sie können beobachtet werden. Ist das ein Trick des Entwicklers? Vermutlich könnte man einen Trick im Code eines Einheitsimpulses anwenden. Doch der Effekt ist doch auf allen Notierungen sichtbar. Und übrigens muss man den Indikator auch nicht spezifisch für jedes Handelsinstrument einstellen oder neu einstellen.
Den perfekten Filter kann es nicht geben, wenn ein Filter mit Hilfe physischer Objekte (Kondensor, Drossler, usw.) gebaut wird. Darum hat sich die Natur schon selbst gekümmert. Doch heißt das dann, dass es in der digitalen Welt niemals einen perfekten Filter geben kann? Die Antwort darauf sollte auf jeden Fall ohne Berücksichtigung der physischen Beschränkungen von Computersystemen (Exaktheit, Rechnergeschwindigkeit, usw.) erfolgen.
Doch zurück zu unserem Indikator. Der eingebaute digitale Filter gehört nicht zu den linearen Filtern. Bei einem Indikator mit eingebautem Filter ist die oben betrachtete Impulsantwort nur ein Spezialfall des Filterns, der gut gegangen ist. Um wirklich zu irgendwelchen weitreichenden Schlussfolgerungen zu kommen, bräuchte man eine besser passende und sorgfältigere Untersuchung.
Fazit
Ich hoffe, dass die Informationen dieses Beitrags dabei helfen, mit einigen Klischees bzgl. der Erzeugung von digitalen Filtern (Indikator) aufzuräumen.
Alles was im Vorangegangenen beschrieben wurde, kann man sich mit Hilfe der vorgeschlagenen Indikatoren noch genauer ansehen. Mit Hilfe der vorgestellten Version des GDynamik-Tests können Sie die Leistung und die potenziellen Fähigkeiten von Cluster-Filtern überprüfen. Das einfache Filter-Beispiel ist zudem vielleicht für Entwickler ein Ansporn, ihre eigenen Filter zu erzeugen.
Zum Abschluss sei mir die folgende Schlussbemerkung gestattet: Die Erzeugung voll funktionsfähiger, nicht hinterherhinkender Indikatoren (digitaler Filter) ist potenziell möglich.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/812
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Lernvideo: MetaTrader Signale-Service
Lernvideo: MetaTrader Signale-Service
 Ständige Terminkontrakte in MetaTrader 5
Ständige Terminkontrakte in MetaTrader 5
 Neuronale Netzwerke - kostengünstig und gut gelaunt: NeuroPro mit MetaTrader 5 verknüpfen
Neuronale Netzwerke - kostengünstig und gut gelaunt: NeuroPro mit MetaTrader 5 verknüpfen
 Ein Indikator zum Anlegen eines Kagi-Diagramms
Ein Indikator zum Anlegen eines Kagi-Diagramms
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Lizar: Dieser Filter kann also an jedem Indikator angebracht werden?
Da der Filter nichtlinear ist, ist die Impulsantwort in verschiedenen Abschnitten unterschiedlich. Daher ist es besser, die Entfaltung zu verwenden - eine Operation der umgekehrten Faltung auf den erforderlichen Abschnitt, für diesen Zweck können Sie die ALGLIB-Bibliothek verwenden.
Stellen Sie das Spektrum für die resultierende Impulsantwort dar. Ein ideales Filter sollte eine vertikale Linie zwischen Unterdrückung und Übertragung aufweisen.
Da der Filter nichtlinear ist, ist die Impulsantwort in verschiedenen Abschnitten unterschiedlich. Daher ist es besser, die Entfaltung zu verwenden - eine Operation der umgekehrten Faltung auf den erforderlichen Abschnitt, für diesen Zweck können Sie die ALGLIB-Bibliothek verwenden.
Stellen Sie das Spektrum für die resultierende Impulsantwort dar. Ein idealer Filter sollte eine vertikale Linie zwischen Unterdrückung und Übertragung aufweisen.
Warum also nicht die Methode der lokalen Annäherung https://chaos.phys.msu.ru/loskutov/PDF/Los_Kotl_Zhur.pdf verwenden?
Sie ermöglicht nicht nur die Vorhersage von Daten, sondern auch deren Filterung. Und theoretisch sollte ein solcher Filter überhaupt keine Verzögerung haben!Die Idee ist sehr ähnlich. Nur muss man hier nicht zwischen verschiedenen Filtern für verschiedene Teile der Zeitreihe wechseln. Hier wird nach Bereichen in der Historie gesucht, die den letzten Zählungen der Reihe ähneln, und diese gefundenen Bereiche werden dann über das Ensemble gemittelt. Dies ist das Ergebnis der Filterung. Das Wichtigste ist, dass genügend Daten in der Historie vorhanden sind, da es sonst möglicherweise keine ähnlichen Diagramme gibt.