
Creating Non-Lagging Digital Filters
Introduction
The article describes one of the approaches to determining a useful signal (trend) in stream data. Small filtering (smoothing) tests applied to market quotes demonstrate the potential for creating non-lagging digital filters (indicators) that are not redrawn on the last bars.
Standard Approach
This approach is based on classical time series smoothing methods. There are lots of articles devoted to this subject both on this and other websites. The results are also classical:
- The changes in trends are displayed with latency;
- Better indicator (digital filter) response achieved at the expense of smoothing quality decrease;
- Attempts to implement non-lagging indicators lead to redrawing on the last samples (bars).
And whereas traders have learned to cope with these things using persistence of economic processes and other tricks, this would be unacceptable in evaluating real-time experimental data, e.g. when testing aerostructures.
The Main Problem
It is a known fact that the majority of trading systems stop performing with the course of time, and that the indicators are only indicative over certain intervals. This can easily be explained: market quotes are not stationary. The definition of a stationary process is available in Wikipedia:
Judging by this definition, methods of analysis of stationary time series are not applicable in technical analysis. And this is understandable. A skillful market-maker entering the market will mess up all the calculations we may have made prior to that with regard to parameters of a known series of market quotes.
Even though this seems obvious, a lot of indicators are based on the theory of stationary time series analysis. Examples of such indicators are moving averages and their modifications. However, there are some attempts to create adaptive indicators. They are supposed to take into account non-stationarity of market quotes to some extent, yet they do not seem to work wonders. The attempts to "punish" the market-maker using the currently known methods of analysis of non-stationary series (wavelets, empirical modes and others) are not successful either. It looks like a certain key factor is constantly being ignored or unidentified.
The main reason for this is that the methods used are not designed for working with stream data. All (or almost all) of them were developed for analysis of the already known or, speaking in terms of technical analysis, historical data. These methods are convenient, e.g., in geophysics: you feel the earthquake, get a seismogram and then analyze it for few months. In other words, these methods are appropriate where uncertainties arising at the ends of a time series in the course of filtering affect the end result.
When analyzing experimental stream data or market quotes, we are focused on the most recent data received, rather than history. These are data that cannot be dealt with using classical algorithms.
Cluster Filter
Cluster filter is a set of digital filters approximating the initial sequence. Cluster filters should not be confused with cluster indicators.
Cluster filters are convenient when analyzing non-stationary time series in real time, in other words, stream data. It means that these filters are of principal interest not for smoothing the already known time series values, but for getting the most probable smoothed values of the new data received in real time.
Unlike various decomposition methods or simply filters of desired frequency, cluster filters create a composition or a fan of probable values of initial series which are further analyzed for approximation of the initial sequence. The input sequence acts more as a reference than the target of the analysis. The main analysis concerns values calculated by a set of filters after processing the data received.
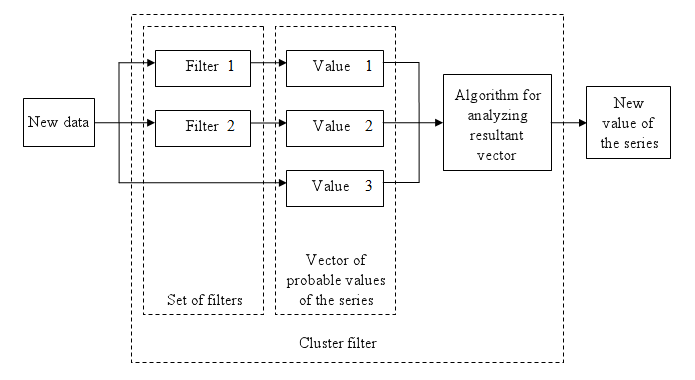
Figure 1. The diagram of a simple cluster filter
In the general case, every filter included in the cluster has its own individual characteristics and is not related to others in any way. These filters are sometimes customized for the analysis of a stationary time series of their own which describes individual properties of the initial non-stationary time series. In the simplest case, if the initial non-stationary series changes its parameters, the filters "switch" over. Thus, a cluster filter tracks real time changes in characteristics.
Cluster Filter Design Procedure
Any cluster filter can be designed in three steps:
1. The first step is usually the most difficult one but this is where probabilistic models of stream data received are formed. The number of these models can be arbitrary large. They are not always related to physical processes that affect the approximable data. The more precisely models describe the approximable sequence, the higher the probability to get a non-lagging cluster filter.
2. At the second step, one or more digital filters are created for each model. The most general condition for joining filters together in a cluster is that they belong to the models describing the approximable sequence.
3. So, we can have one or more filters in a cluster. Consequently, with each new sample we have the sample value and one or more filter values. Thus, with each sample we have a vector or artificial noise made up of several (minimum two) values. All we need to do now is to select the most appropriate value.
An Example of a Simple Cluster Filter
For illustration, we will implement a simple cluster filter corresponding to the above diagram, using market quotes as input sequence. You can simply use closing prices of any time frame.
1. Model description. We will proceed on the assumption that:
- The approximable sequence is non-stationary, i.e. its characteristics tend to change with the course of time.
- The closing price of a bar is not the actual bar price. In other words, the registered closing price of a bar is one of the noise movements, like other price movements on that bar.
- The actual price or the actual value of the approximable sequence is between the closing price of the current bar and the closing price of the previous bar.
- The approximable sequence tends to maintain its direction. That is, if it was growing on the previous bar, it will tend to keep on growing on the current bar.
2. Selecting digital filters. For the sake of simplicity, we take two filters:
- The first filter will be a Simple Moving Average calculated based on the last two closing prices. I believe this fits well in the third assumption we specified for our model.
- Since we have a non-stationary filter, we will try to also use an additional filter that will hopefully facilitate to identify changes in characteristics of the time series. I've chosen an Exponential Moving Average as this option seemed reasonable and quite fitting to me. This is due to the fact that EMA is faster than MA, so it should not cause any lags along the trend and has better response to noise. The EMA will also be calculated based on the last two closing prices.
3. Selecting the appropriate value for the cluster filter.
So, with each new sample we will have the sample value (closing price), as well as the value of MA and EMA. The closing price will be ignored according to the second assumption specified for our model. Further, we select the МА or ЕМА value based on the last assumption, i.e. maintaining trend direction:
For an uptrend, i.e. CF(i-1)>CF(i-2), we select one of the following four variants:
if CF(i-1)<MA(i) and CF(i-1)<EMA(i), then CF(i)=MIN(MA(i),EMA(i));
if CF(i-1)<MA(i) and CF(i-1)>EMA(i), then CF(i)=MA(i);
if CF(i-1)>MA(i) and CF(i-1)<EMA(i), then CF(i)=EMA(i);
if CF(i-1)>MA(i) and CF(i-1)>EMA(i), then CF(i)=MAX(MA(i),EMA(i)).
For a downtrend, i.e. CF(i-1)<CF(i-2), we select one of the following four variants:
if CF(i-1)>MA(i) and CF(i-1)>EMA(i), then CF(i)=MAX(MA(i),EMA(i));
if CF(i-1)>MA(i) and CF(i-1)<EMA(i), then CF(i)=MA(i);
if CF(i-1)<MA(i) and CF(i-1)>EMA(i), then CF(i)=EMA(i);
if CF(i-1)<MA(i) and CF(i-1)<EMA(i), then CF(i)=MIN(MA(i),EMA(i)).
Where:
- CF(i) – value of the cluster filter on the current bar;
- CF(i-1) and CF(i-2) – values of the cluster filter on the previous bars;
- MA(i) – value of the Simple Moving Average on the current bar;
- EMA(i) – value of the Exponential Moving Average on the current bar;
- MIN – the minimum value;
- MAX – the maximum value;
Program Code and Cluster Filter Performance
The code of the indicator with our cluster filter is not any more complex than the code of the moving average. It does not feature any knowhow techniques, so there is no point in reviewing it. The source code is attached to the article.
Without wasting time, you can watch the video provided below to see the performance of our indicator:
Video 1. Performance of a simple cluster filter
Even though the filter design process may have looked more like conjuring rather than a strictly mathematical approach, the video clearly demonstrates that the behavior of the cluster filter line is more adequate than that of individual moving averages. It is especially obvious over the saw-tooth sections of the initial series. If it was not impressive enough for some of you, we can further compare the cluster filter with JJMA, which is considered to be one the best indicators. The next video shows a competition of JJMA and our cluster filter over the same section. I have tried to select JJMA parameters so that its line could match our indicator line to the maximum.
Video 2. Simple cluster filter vs. JJMA
Our filter, on the average, demonstrates about the same performance as JJMA on any time series. But while JJMA is already at its best, our cluster filter can further be improved.
Advanced Smoothing Effect
Until now, there was no evidence that cluster filters are capable of smoothing an input sequence without latency. To achieve this result, one requires a more complex filter than the one considered above.
For illustration purposes, I have developed a GMomentum test indicator. It contains two indicator lines:
- Blue line - classical momentum.
- Red line - classical momentum smoothed by the digital cluster filter with a more complex algorithm.
The settings of the indicator cover various test options specifically prepared for the article. In the tests described below, we will use a relative momentum as described by William Blau. When carrying out your own experiments, you can use other variations of momentum - the results will be the same. A detailed description of the indicator, as well as instructions for download and use can be found in the description of the indicator.
There is no special reason behind the use of Momentum in the article. The momentum line is quite noise-contaminated and therefore the performance of the filter will in my opinion be more illustrative. So, you run the GMomentum test indicator and analyze the behavior of the red line in comparison with the blue one.
First off, let's take a look at one interesting thing. For this purpose, before you run the indicator, set the "Filter" parameter to "Test No.1 Advance". The filter settings in this mode quite often reveal what can be called a "leading effect". When testing, you will not be able to see the smoothing of the entire initial line of the momentum. The filter watches for areas where the possibility to get a leading effect is good. No wonder, this is not always successful. And yet, it occurs often enough to notice.
One of the most illustrative parts of the filter's performance is displayed in the chart below.
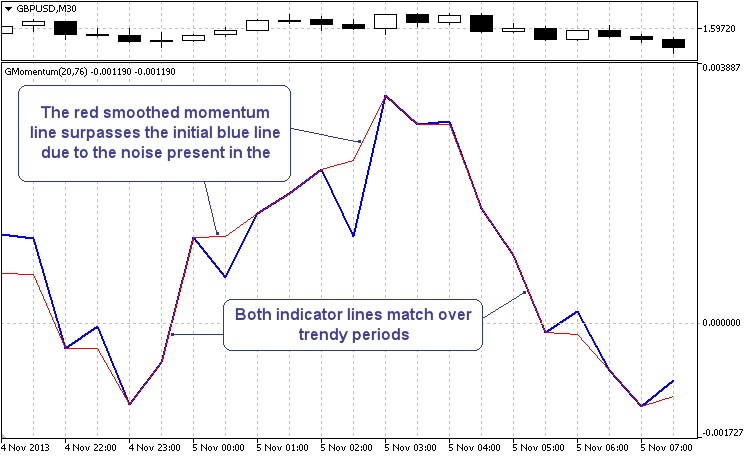
Figure 2. Leading effect in smoothing of the momentum line
It should be noted that it only seems to be leading filtering. This effect occurs exclusively due to noise movements of the momentum line, rather than due to the filter being ahead of time. Similar studies of other indicators (from a simple MA to JJMA) confirm that the leading effect of smoothing can be observed in each of them. The smaller the specified period, the more frequently the effect is observed. The latest studies suggest that the effect can be enhanced. It all depends on the method of generating a vector of probable values and its analysis.
The Cobra Effect
Those of you who have already seen the indicator in action, could notice another anomaly. The indicator line on the last incomplete bar does not always follow the price. For example, the price may be going up, while the indicator is moving down, and vice versa. When the market is fast or when looked at in the visualizer, it sometimes resembles a cobra's tongue tracking prey.
Video 3. Leading effect of smoothing and the cobra effect
Ahead-of-the-Trend Errors
We could see above that when the initial line of the momentum goes against the trend (becomes noisy), it results in the leading effect of the smoothed line over the initial line. Apparently, the momentum line can also make a wrong move in the other direction, i.e. unexpectedly shoot far in the direction of the trend, sometimes lingering far too long, even though the trend has already reversed. It would be logical if the filter could slow down such movements.
Let's see how the algorithm filters these ahead-of-the-trend errors. For this purpose, before you run the indicator, you should set the "Filter" parameter to "Test No.2 Smoothing". The operation of the cluster filter during this test is divided into two parts.
The short indicator name "GMomentum(Parameter 1, Parameter 2)" displayed in the chart subwindow has two parameters in brackets. If the second parameter is -1, the algorithm makes an attempt to fix (smoothen) ahead-of-the-trend errors. If the second parameter is equal to or greater than zero, the advanced smoothing settings are brought into action.
The video provided below demonstrates the filter operation upon changing its sensitivity from the minimum to the acceptable value and back. To get the effect as shown in the video, the filter sensitivity can be controlled (provided that the indicator window is active) using Up and Down keys.
Video 4. Filtering ahead-of-the-trend errors.
The above video suggests that despite the sudden movements of the price and the initial line of the momentum, the momentum line is smoothed without lag as the filter sensitivity increases. Upon maximum smoothing, we get acceptable entry points.
On a side note, flat areas present an issue for the majority of indicators. Here, however, some of them easily degenerate into a nearly straight line even with the existing settings. Theoretically, this technique can be used to improve any of the existing indicators without producing an additional lag. From the practical standpoint, it needs checking.
In the next video, please focus your attention on how the filter flattens major peaks of the initial momentum line and draws a smoother trend line closer to the price movement almost without lag. The explanation as to why this is so is provided in the article about William Blau's indicators.
Video 5. Smoothing of peaks of the initial momentum line.
The impressive results achieved are not the same over the entire history of quotes. But considering the fact that the momentum has a lot of noise and that the indicator has been implemented solely to demonstrate filtering of stream data without lags, we can deem it quite acceptable. In addition, it should be noted that the indicator is not redrawn.
Impulse Response
The study of parameters of the momentum with a built-in filter may appear to be quite interesting. For example, the impulse response provides a good illustration of how and where peaks disappear from the indicator line. To perform the test, the "Filter" parameter should be set to "Test No.3 Impulse". During the test, every 1024th bar receives a unit impulse. After running the indicator, find the relevant place in the chart. It should look like this:
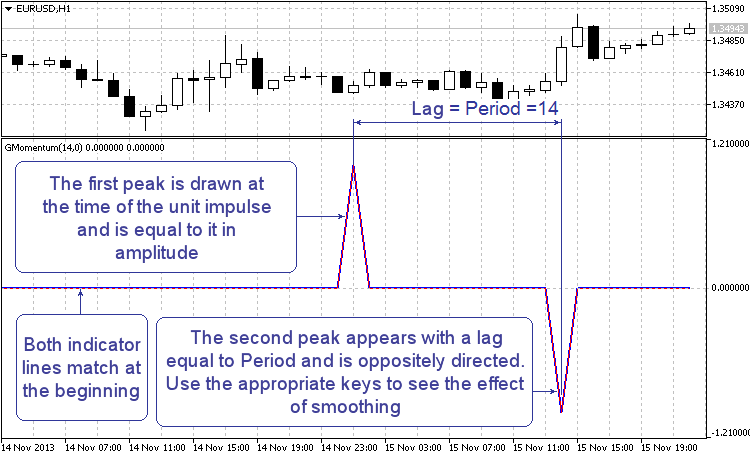
Figure 3. Momentum impulse response
When the indicator is running, the filter is disabled. You will therefore be able to see two peaks on the blue and red line: one peak that appeared at the time of the unit impulse and that is equal to it, and the other oppositely directed peak that appeared after the specified number of periods. This is what impulse response of the "bare" momentum looks like. Further, gradually increase or decrease the filter sensitivity using Up and Down keys. You should be able to get something like this:
Video 6. Momentum impulse response
As can be seen, the second peak is completely flattened by the filter, whereas the first one remains absolutely intact. The filter fixes all momentum effects and accurately reconstructs the initial picture: a unit impulse by itself. There are no lags. There is no distortion of the amplitude or the form of the unit impulse. Can it be the perfect filter in action?
The Perfect Filter
There is one material factor which does not allow us to immediately deem the filter under question to be perfect. This will be explained a little later.
It is believed that the perfect filter cannot exist and that all filters (indicators) lag. But then how can we explain the results obtained? All of them are presented as something that can be observed. Is it a developer's trick? One could probably use a coding trick in a unit impulse code. But the effect can be observed on any quotes. Besides, there is no need to specifically set or reset the indicator for each trading instrument.
The perfect filter cannot exist when a filter is built using physical objects (condenser, inductor, etc.). This has been taken care of by nature itself. Yet, is the existence of the perfect filter impossible in the digital world? The answer to this question should certainly be given without regard for physical limits of computer systems (accuracy, computing speed, etc.).
Let's get back to our indicator. The built-in digital filter does not belong to linear filters. For an indicator with built-in filter, the impulse response considered above is just a special case of filtering that happened to turn out well. To be able to draw any far-reaching conclusions, a more adequate and careful study is required.
Conclusion
I hope that the information provided in the article will help break some stereotypes about creating digital filters (indicators).
All the things described can be looked into using the proposed indicators. The introduced version of GMomentum test will allow you to assess the performance and potential capabilities of cluster filters, while the simple filter example might give an impulse to the developers to create their own filters.
Finally, I take the liberty of drawing the following conclusion: creating fully-featured non-lagging indicators (digital filters) is potentially possible.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/812
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Offline Charts in the New MQL4
Offline Charts in the New MQL4
 Data Structure in MetaTrader 4 Build 600 and Higher
Data Structure in MetaTrader 4 Build 600 and Higher
 Indicator for Kagi Charting
Indicator for Kagi Charting
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Lizar: So this filter can be attached to any indicator?
Since the filter is nonlinear, the impulse response at different sections is different. Therefore, it will be better to use deconvolution - an operation of inverse convolution on the necessary section, for this purpose you can use ALGLIB library.
And plot the spectrum for the resulting impulse response. An ideal filter should have a vertical line between suppression and transmission.
Since the filter is nonlinear, the impulse response at different sections is different. Therefore, it will be better to use deconvolution - an operation of inverse convolution on the necessary section, for this purpose you can use ALGLIB library.
And plot the spectrum for the resulting impulse response. An ideal filter should have a vertical line between suppression and transmission.
So why not use the local approximation method https://chaos.phys.msu.ru/loskutov/PDF/Los_Kotl_Zhur.pdf ?
It allows not only predicting data, but also filtering. And, theoretically, such a filter should have no delay at all!The idea is very similar. Only here you don't need to switch between different filters for different parts of the time series. Here we search for areas in the history similar to the last counts of the series, and then these found areas are averaged over the ensemble. This is the result of filtering. The main thing is that there should be enough data in the history, otherwise there may be no similar plots.