
Creación de filtros digitales sin retardo temporal
Introducción
En el presente artículo se estudia una de las aproximaciones para determinar la utilidad de una señal (tendencia) de flujo de datos. Algunos tests para el filtrado (suavización) de las cotizaciones de la bolsa, bastante útiles, demuestran la posibilidad potencial de crear filtros digitales (indicadores) que no sufran retrasos temporales y no se redibujen en las últimas barras.
Aproximación habitual
Esta aproximación se basa en los métodos clásicos de suavización de las series temporales. Sobre este tema hay multitud de artículos, tanto en esta página, como en otras. Los resultados obtenidos son igualmente clásicos:
- El cambio de tendencia se muestra con retraso;
- Se debe pagar por el aumento de reacción del indicador (filtro digital) con una disminución en la calidad de la suavización;
- Los intentos de implementar indicadores sin retardo normalmente provocan que se redibuje en los últimos informes (barras).
Aunque los traders han aprendido a luchar con este hecho, utilizando la inercia de los procesos económicos y otras astucias, esto sería inaceptable al valorar datos experimentales en tiempo real, por ejemplo al experimentar con estructuras aéreas.
El problema principal
No es un secreto que la mayoría de sistemas comerciales dejan de funcionar con el paso del tiempo. O que los indicadores sólo son indicativos en ciertos intervalos. La explicación es sencilla: las cotizaciones del mercado no son estacionarias. Podemos encontrar una definición bastante sencilla del proceso estacionario en la Wikipedia:
A juzgar por la definición, los métodos de análisis de las series temporales estacionarias no tienen razón de ser en el análisis técnico. Esto resulta comprensible, en cuanto calculamos las carcterísticas de una serie conocida de cotizaciones de bolsa, en el mercado entrará algún market maker y hará que todos nuestros cálculos dejen de tener sentido.
A pesar de que este hecho sea obvio, una gran cantidad de indicadores se construyen en base a la teoría del análisis de las series temporales estacionarias. Un ejemplo de tales indicadores serían las medias móviles y sus modificaciones. En cualquier caso, se están intentando crear indicadores que sean capaces de adaptarse. Se supone que deben tener en cuenta en uno u otro grado la "no-estacionaridad" de las cotizaciones en la bolsa, pero por ahora no se ha logrado el milagro. Los intentos de "castigar" al market-maker utilizando los métodos de análisis de series no estacionarias conocidos a día de hoy (ondículas, modos empíricos y otros), tampoco han tenido éxito. Parece ser que hay algún factor clave que es constantemente ignorado o no se puede identificar.
El motivo principal de esta situación general es que los métodos utilizados no están pensados para trabajar con el flujo de datos. Todos ellos (o casi todos) se desarrollaron para analizar datos ya conocidos de antemano o, como se conoce en la teminología del análisis técnico, datos históricos. Estos métodos son cómodos, por ejemplo, en geofísica: la tierra "tiembla", obtenemos un sismograma y luego lo estudiamos durante un par de meses. Es decir, se pueden aplicar allá donde las indeterminaciones, aparecidas al final de las series temporales al llevarse a cabo la filtración, ejercen una influencia significativa en el resultado final.
Al analizar los flujos de datos experimentales o las cotizaciones en la bolsa, el máximo interés se concentra en los últimos datos recibidos, no en la historia. Precisamente esos son los datos con los que no saben manejarse los algoritmos clásicos.
Filtro cluster
Filtro cluster (ingl. cluster — racimo, coágulo, manojo) - conjunto de filtros digitales que se aproximan a la secuencia inicial. Los filtros cluster no deben ser confundidos con los indicadores cluster.
El filtro cluster es cómodo de usar en el análisis de las series temporales no estacionarias en tiempo real, en otras palabras, el flujo de datos. Esto significa que este tipo de filtro representa un mayor interés, por ejemplo, no para suavizar valores ya conocidos de la serie temporal, sino para lograr los valores suavizados más probables de la nueva información, obtenida en tiempo real.
A diferencia de los diversos métodos de descomposición (descomposición de componentes) o simplemente de los filtros de la frecuencia deseada, los filtros cluster crean una composición o abanico de valores probables de la serie inicial, que en lo sucesivo serán sometidos a un análisis adicional para la aproximación a la secuencia inicial. La secuencia de entrada juega más un papel de referencia que de objeto de análisis. El análisis principal concierne a los valores calculados por el conjunto de filtros después de procesar el dato recibido.
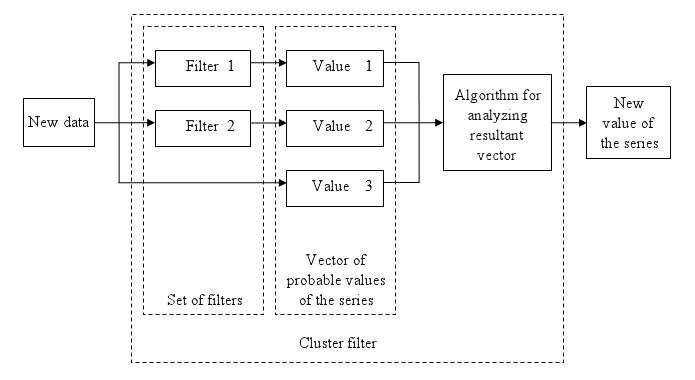
Dibujo 1. Esquema de un filtro cluster sencillo
En general, cada filtro conectado al cluster posee sus propias características individuales y no está relacionado con otros en modo alguno. A veces estos filtros están configurados para analizar una cierta serie temporal estacionaria propia, que describe propiedades individuales de la serie no estacionaria inicial. En el caso más sencillo, si la serie no estacionaria inicial cambia sus parámetros, entonces tiene lugar la "conmutación" entre filtros. De esta forma, el filtro cluster rastrea el cambio de características en tiempo real.
Procedimiento de diseño de los filtros cluster
Cualquier filtro cluster puede ser creado en tres etapas:
1. La primera etapa suele ser la más complicada, pero es precisamente en esta etapa cuando se forman los modelos probables de los flujos de datos recibidos. La cantidad de estos modelos puede ser de una magnitud muy grande, cualquiera. Los modelos no siempre tienen relación con los procesos físicos que influyen en los datos aproximativos. Cuanto mayor sea la precisión con la que los modelos describan la secuencia aproximativa, mayor será la probabilidad de obtener un filtro cluster sin retardos.
2. En la segunda etapa se crean uno o varios filtros según cada modelo. La condición más general para unir filtros en un grupo (cluster) es que pertenezcan a modelos que describan una secuencia aproximativa.
3. Así, podemos tener uno o más filtros en un grupo. Propiamente, en cada nuevo informe tenemos la magnitud del informe mismo y uno o más valores de los filtros. De esta forma, en cada informe tenemos un vector o ruido artificial, formado por varios valores (dos, como mínimo). Lo único que hay que hacer ahora es elegir el valor más adecuado.
Ejemplo de filtro cluster simple
A modo de ejemplo, implementaremos un filtro cluster simple, que se corresponde con el esquema representado en el dibujo 1. Como secuencia de entrada tomaremos las cotizaciones. Podemos tomar simplemente los precios de cierre de cualquier time frame.
1. Descripción del modelo elegido. Partiremos de las siguientes suposiciones:
- La secuencia aproximativa es no estacionaria, es decir, tiene la propiedad de cambiar sus características con el paso del tiempo.
- El precio de cierre de la barra no constituye el precio verdadero de la barra. Es decir, que el precio fijado del cierre de la barra es uno de los moviemientos del ruido, al igual que el resto de los movimientos del precio en esta barra
- El precio real o el valor real de la secuencia aproximativa se encuentra entre el precio de cierre de la barra actual y el precio de cierre de la barra anterior.
- La secuencia aproximativa tiende a mantener su dirección. Es decir, si en la barra anterior estaba creciendo, en la barra actual tenderá a mantener el crecimiento.
2. Seleccionamos los filtros digitales. Para que sea más sencillo tomaremos dos filtros:
- El primer filtro será una media móvil simple (Simple Moving Average), calculada conforme a los dos últimos precios de cierre. A mi entender, esto encaja bien con la tercera condición de nuestro modelo.
- Dado que el proceso no es estacionario, entonces probaremos a introducir un filtro adicional, con la esperanza de que esto ayude de alguna forma a captar los cambios en las características de la serie temporal. Yo, por mi parte, he elegido la media móvil exponencial (Exponential Moving Average). Lo he hecho sólo porque la EMA es más rápida que la MA y no debería dar retrasos a lo largo de la tendencia y reacciona mejor al ruido. La EMA también la calcularemos conforme a los dos últimos precios de cierre.
3. Elegimos el valor más adecuado para el filtro cluster.
Así, en cada nuevo informe tendremos el valor del propio informe (precio de cierre), así como el valor de la MA y de la EMA. Ignoraremos el precio de apertura, partiendo de la segunda condición de nuestro modelo. Después elegimos el valor de la МА o la ЕМА, partiendo de la última condición del modelo, es decir, de la condición de la dirección de la tendencia:
Para una tendencia ascendente, es decir, CF(i-1)>CF(i-2), elegimos una de las cuatro posibilidades siguientes:
si CF(i-1)<MA(i) y CF(i-1)<EMA(i), entonces CF(i)=MIN(MA(i),EMA(i));
si CF(i-1)<MA(i) y CF(i-1)>EMA(i), entonces CF(i)=MA(i);
si CF(i-1)>MA(i) y CF(i-1)<EMA(i), entonces CF(i)=EMA(i);
si CF(i-1)>MA(i) y CF(i-1)>EMA(i), entonces CF(i)=MAX(MA(i),EMA(i)).
Para una tendencia descendente, es decir, CF(i-1)<CF(i-2), elegimos una de las cuatro posibilidades siguientes:
si CF(i-1)>MA(i) y CF(i-1)>EMA(i), entonces CF(i)=MAX(MA(i),EMA(i));
si CF(i-1)>MA(i) y CF(i-1)<EMA(i), entonces CF(i)=MA(i);
si CF(i-1)<MA(i) y CF(i-1)>EMA(i), entonces CF(i)=EMA(i);
si CF(i-1)<MA(i) y CF(i-1)<EMA(i), entonces CF(i)=MIN(MA(i),EMA(i)).
Donde:
- CF(i) – es el valor del filtro cluster en la barra actual;
- CF(i-1) и CF(i-2) – es el valor del filtro cluster en las barras anteriores;
- MA(i) – es el valor de la media móvil simple en la barra actual;
- EMA(i) – es el valor de la media móvil exponencial en la barra actual;
- MIN – es el valor mínimo;
- MAX – es el valor máximo;
Código del programa y resultados del trabajo del filtro cluster
El código de indicador con nuestro filtro cluster no es más complejo que el código de la media móvil. Por eso no tiene sentido analizarlo aquí, ya que no contiene ningún conocimiento fundamental. La fuente se adjunta al artículo.
Sin perder un instante, podemos ver un ejemplo del funcionamiento de nuestro indicador en el vídeo:
Vídeo 1. Resultado del funcionamiento de un filtro cluster simple
A pesar de que la creación del filtro ha parecido más fruto de un hechizo que de una aproximación matemática, en el vídeo podemos notar con claridad que la línea del filtro cluster se comporta de manera adecuada que las medias móviles tomadas por separado. Esto se ve bien especialmente en los intervalos con forma de sierra de la serie inicial. Si alguien no se ha sentido impresionado, entonces podemos compararlo con JJMA, considerado uno de los mejores indicadores. En el siguiente vídeo podemos ver la misma sección, pero en ella compiten ahora JJMA y nuestro filtro. He tratado de elegir los parámetros de JJMA de tal manera que su línea del máximo coincidiera con nuestro indicador.
Vídeo 2. Comparación del filtro cluster simple y JJMA
De media, nuestro filtro no pierde contra JJMA en cualquier serie temporal. Pero, mientras que a JJMA ya se le ha sacado todo el jugo, nuestro filtro cluster aún puede ser mejorado.
Efecto de la suavización en adelantado
Hasta ahora no disponemos de ninguna confirmación de que los filtros cluster sean capaces de suavizar la secuencia inicial sin retardo. Para alcanzar un resultado semejante, es necesario crear un filtro más complicado del que hemos visto más arriba.
Para la demostración se ha hecho el indicador GMomentum test. Contiene dos líneas de indicador:
- La azul es el momentum clásico.
- La roja es el momentum clásico suavizado con el filtro digital cluster, en el que se ha implementado un algoritmo más complejo.
En la configuración del indicador hay variantes diferentes de pruebas especialmente preparadas para el artículo. En las pruebas descritas más abajo se usa un momentum relativo, como el descrito por William Blau. Para realizar vuestros propios experimentos podéis usar otras variaciones de momentum, los resultados serán los mismos. Podéis encontrar una descripción detallada y las instrucciones de instalación y uso del indicador en la descripción del indicador mismo.
No tengo ningún argumento especial para elegir Momentum para ese artículo, simplemente la línea de momentum está bastante contaminada por el ruido, y por ello el funcionamiento del filtro, a mi entender, será más ilustrativo. Y bien, ponga en marcha el indicador GMomentum test y estudie cómo se comporta la línea roja en comparación con la azul.
Para empezar, analizaremos un momento bastante curioso. Para ello, al iniciar el indicador es necesario establecer el parámetro "Filter" en "Test No.1 Advance". En este modo, la configuración del filtro es tal que con bastante frecuencia se manifiesta un efecto que se puede denominar adelantado. Al realizar la simulación podrá ver la suavización de toda la línea inicial de momentum. El filtro busca los segmentos donde la posibilidad de obtener un efecto en adelantado es buena. No debe sorprendernos que esto no siempre tenga éxito. Pero sucede con la frecuencia sufieciente como para notarlo.
En el gráfico de más abajo se muestra uno de los sectores más ilustrativos del funcionamiento del filtro.
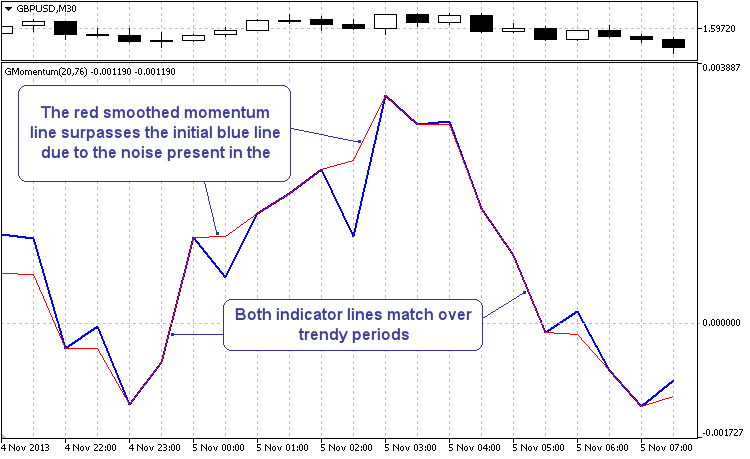
Dibujo 2. El efecto en adelantado durante la suavización de la línea momentum
Merece la pena señalar que se trata sólo de la visibilidad de la filtración en adelantado. Esta efecto ocurre, exclusivamente, a causa de los movimientos del ruido presentes en la misma línea de momentum, y no porque el filtro se haya adelantado al tiempo. Investigaciones semejantes con otros indicadores (desde una MA simple, hasta JJMA) confirman que el efecto de suavización en adelantado se puede observar en cada uno de ellos. Y cuanto menor sea el periodo establecido, con más frecuencia se manifestará esto. Los últimos estudios demuestran que el efecto se puede intensificar. Todo depende del método de formación del vector de valores probables y su análisis.
El Efecto Cobra
Aquel que haya visto el indicador en funcionamiento, podrá prestar atención a otra anomalía más. La línea del indicador en la última barra no formada no siempre sigue al precio. Por ejemplo, el precio puede estar creciendo, y el indicador se mueve hacia abajo. Y al contrario. Cuando el mercado se mueve rápido o cuando se mira al visualizador, a veces recuerda la lengua de una cobra que esté rastreando a una presa.
Vídeo 3. La suavización en adelantado y el efecto cobra
Errores de anticipación a la tendencia
Más arriba se ha demostrado que cuando la línea inicial de momentum va en contra de la tendencia (hace ruido), esto provoca el efecto de adelantamiento de la línea inicial sobre la línea suavizada. Obviamente, la línea de momentum puede equivocarse hacia el otro lado, es decir, dar un salto inesperado lejos en la dirección de la tendencia, e incluso mantenerse mucho tiempo allí, aunque la tendencia ya haya virado. Sería lógico, si el filtro comenzara a frenar movimientos de este tipo.
Vamos a ver cómo funciona el algoritmo al realizar el filtrado de tales errores, que preceden a la tendencia. Para ello, al iniciar el indicador, es necesario establecer el parámetro "Filter" en "Test No.2 Smoothing". El funcionamiento del filtro cluster durante esta prueba se divide en dos partes.
En el nombre breve del indicador "GMomentum(Parámetro 1, Parámetro 2)", representado en la subventana, hay dos parámetros entre paréntesis. Si el segundo parámetro es igual a -1, entonces tiene lugar un intento de corregir (suavizar) los errores que anteceden a la tendencia. Si el segundo parámetro es igual o mayor a cero, entonces se conectan las configuraciones para la obtención de la suavización en adelantado.
En el vídeo se puede ver el funcionamiento del filtro al variar su sensibilidad desde el mínimo hasta un valor aceptable y de vuelta. En el indicador, para manejar la sensibilidad (con la ventana del indicador activa) pulse las teclas up y down, para conseguir un efecto semejante al del vídeo.
Vídeo 4. Filtrado de errores adelantados a la tendencia.
En el vídeo de arriba se puede ver que, a pesar de los movimientos bruscos del precio y la línea de momentum, la suavización de la línea de momentum tiene lugar sin retardo cuando se aumenta la sensibilidad del filtro . Con una suavización máxima, obtenemos puntos de entrada aceptables.
A propósito, los segmentos en plano representan un problema para la mayoría de los indicadores. Aquí, incluso con esta configuración, algunos de ellos degeneran en una línea plana con gran facilidad. En teoría, usando esta técnica se puede mejorar cualquiera de los indicadores existentes sin crear un retardo adicional. Pero eso es en teoría, hay que comprobarlo.
En el siguiente vídeo preste atención a que el filtro "aplana" los picos más acusados de la línea inicial de momentum y prácticamente sin retardo dibuja la tendencia que, por cierto, se acerca al movimiento del precio y ya es más plana. La explicación de por qué esto es así, se encuentra en el artículo sobre el indicador de William Blau.
Vídeo 5. Suavización de los picos de la línea inicial de momentum.
El resultado obtenido no impresiona tanto en lo que respecta a toda la historia de las cotizaciones. Pero teniendo en cuenta el hecho de que momentum acusa un gran movimiento de ruido, y el hecho de que el indicador se ha hecho sólo para demostrar el filtrado del flujo de datos sin retardo temporal, se lo puede considerar bastante aceptable. Además, hay que destacar que el indicador no se redibuja.
Respuesta al impulso
Las investigaciones de las carcaterísticas de momentum con el filtro incorporado pueden resultar muy laboriosas. Por ejemplo, la respuesta al impulso demuestra bien en qué manera y dónde desaparecen los picos en la línea del indicador. Para realizar la prueba es necesario establecer el parámetro "Filter" en "Test No.3 Impulse". Durante la prueba, cada barra número 1024 recibe un impulso único. Tras iniciar el indicador, encuentre ese momento en el gráfico. Debe tener el aspecto siguiente:
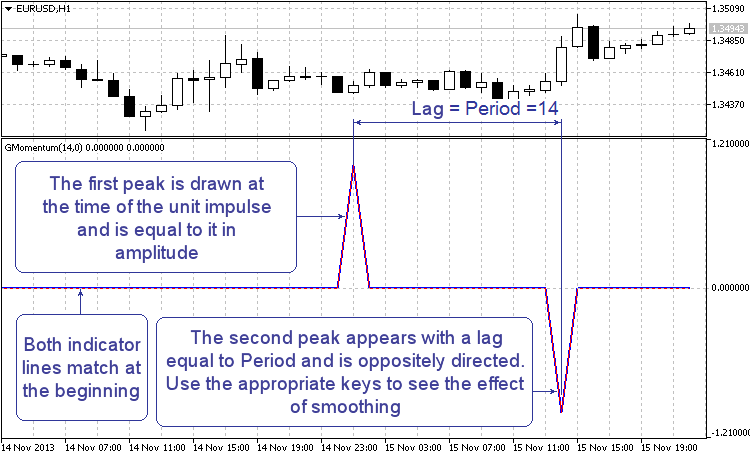
Dibujo 3. Respuesta al impulso de momentum
Al iniciar el indicador, el filtro está desconectado. Por eso usted verá dos picos en la línea roja y la azul. Un de los picos tendrá lugar en el momento del impulso y será igual al mismo; el otro estará dirigido en dirección opuesta y aparecerá tras el número de periodos indicado. Este es el aspecto preciso que tiene la respuesta al impulso del momentum "desnudo". A continuación, con la ayuda de los botones Up y Down, aumente o disminuya gradualmente la sensibilidad del filtro. Debería obtener algo semejante a esto:
Vídeo 6. Respuesta al impulso de momentum
Como puede ver, el filtro "aplana" bajo la raíz el segundo pico y no toca en absoluto el primero. El filtro corrige por completo los efectos de momentum y reconstruye con precisión la imagen inicial: un impulso único en campo abierto. No existe retardo alguno. No existe tampoco ninguna alteración en la amplitud y la forma del impulso. ¿Qué es esto? ¿El funcionamiento de un filtro perfecto?
El filtro perfecto
Hay un factor muy significativo que no permite considerar perfecto el filtro estudiado. Pero de eso hablaremos un poco más abajo.
Existe la idea fija de que no puede existir un filtro perfecto. La idea de que todos los filtros (o indicadores) sufren retardo. Entonces, ¿cómo explicar los resultados obtenidos? Los resultados están presentados como algo que puede ser observado y estudiado. ¿Se trata de alguna astucia del programador? Posiblemente se puedan hacer trucos en el código con un impulso único. Pero el efecto se manifiesta en cualquier cotización. Además, no hay necesidad alguna de configurar o reconfigurar el indicador conforme a cada instrumento comercial.
Cuando construimos un filtro de objetos físicos (condensador, inductor, ect), no puede resultar un filtro perfecto. De esto se ha ocupado la propia naturaleza. Pero cuando trabajamos con el mundo digital, ¿acaso sigue siendo imposible la construcción del filtro perfecto? La respuesta a este problema hay que darla dejando a un lado las limitaciones físicas de los sistemas de computación (precisión, velocidad del cálculo, etc).
Volvamos a nuestro indicador. El filtro digital incorporado no pertenece al tipo de los filtros lineales. Y lo que más arriba hemos denominado respuesta a un impulso, para un filtro incorporado, no es más que un caso afortunado de filtrado en concreto. Para llegar a una consclusión duradera, hay que llevar a cabo una investigación más adecuada y minuciosa.
Conclusión
Espero que el material mostrado en el artículo rompa con ciertos estereotipos, en lo que respecta a la construcción de filtros digitales (indicadores).
Todo lo descrito se puede investigar con la ayuda de los indicadores propuestos. La versión presentada de GMomentum test permite a todos valorar la capacidad de trabajo y las posibilidades potenciales de los filtros cluster. Y un ejemplo sencillo de un filtro simple puede animar a los desarrolladores a crear uno propio.
Para terminar, me permitiré la libertad de manifestar la siguiente conclusión: la creación de indicadores (filtros digitales) completos y que no sufran retardos es potencialmente posible.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/812
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Pegado de contrato de futuros en MetaTrader 5
Pegado de contrato de futuros en MetaTrader 5
 Cómo trabajar con el módem GSM de un experto de MQL5
Cómo trabajar con el módem GSM de un experto de MQL5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Lizar: Entonces, ¿este filtro puede acoplarse a cualquier indicador?
Dado que el filtro no es lineal, la respuesta al impulso en diferentes secciones es diferente. Por lo tanto, será mejor utilizar la deconvolución - una operación de convolución inversa en la sección necesaria, para ello puede utilizar la biblioteca ALGLIB.
Y trazar el espectro de la respuesta al impulso resultante. Un filtro ideal debe tener una línea vertical entre la supresión y la transmisión.
Dado que el filtro no es lineal, la respuesta al impulso en diferentes secciones es diferente. Por lo tanto, será mejor utilizar la deconvolución - una operación de convolución inversa en la sección necesaria, para ello puede utilizar la biblioteca ALGLIB.
Y trazar el espectro de la respuesta al impulso resultante. Un filtro ideal debe tener una línea vertical entre la supresión y la transmisión.
Entonces, ¿por qué no utilizar el método de aproximación local https://chaos.phys.msu.ru/loskutov/PDF/Los_Kotl_Zhur.pdf ?
No sólo permite predecir datos, sino también filtrarlos. Y, teóricamente, ¡un filtro así no debería tener ningún retraso!La idea es muy parecida. Sólo que aquí no es necesario cambiar entre diferentes filtros para diferentes partes de la serie temporal. Aquí buscamos segmentos en la historia que sean similares a los últimos recuentos de la serie, y luego estos segmentos encontrados se promedian sobre el conjunto. Este es el resultado del filtrado. Lo principal es que haya suficientes datos en el historial, de lo contrario puede que no haya parcelas similares.