ZigZag Göstergesi: Yeni Yaklaşım ve Yeni Çözümler
545
0
Giriş
Her yatırımcı, verilen veya daha yüksek büyüklükteki fiyat hareketlerinin analizine yönelik ZigZag göstergesini kesinlikle bilir. Bir ZigZag çizgisi, düğümleri fiyat grafiğinin yüksek ve düşük noktalarında bulunan kesik bir çizgidir.
Bu göstergenin birçok varyasyonu vardır: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16. Yine de birçok MQL5 program geliştiricisi kendi "ideal" ZigZag'larını yaratmaya heveslidir. ZigZag göstergesinin ana dezavantajları gecikmeler, şüpheli düğümlerin (harici çubuk) yanlış işaretlenmesi ve memnun edici olmayan performanstır.
Bana göre en şık ZigZag uygulaması Yuri Kulikov (Yurich) tarafından önerilmiştir. Bunun yanı sıra "Layman's Notes: ZigZag..." ve "Show Must Go On, or Once Again about ZigZag" gibi oldukça iyi MQL4 makaleleri vardır. Konu büyük ölçüde araştırılmış gibi görünüyor ve çok sayıda yayın mevcut. Yine de bu konuda insanı çeken bir şey var. Şimdi, özellikle gelişmiş bir ZigZag göstergesi oluşturma olanağında da ilgimi çekti.
Bu makale, Zarflar göstergesini kullanarak gelişmiş bir ZigZag oluşturmak için bir yöntemi açıklamaktadır. Çoğu ZigZag düğümünün Zarf bantlarının sınırları içinde yer aldığı bir Zarflar serisi için belirli bir giriş parametresi kombinasyonu bulunabileceği varsayılır.
Gelişmiş ZigZag Göstergesi Oluşturma Yöntemi
Bir hedef belirleyeceğiz: iki düğümün - mevcut ve tahmin edilen düğüm - koordinatlarını bulmak (Şekil 1). Mevcut düğüm, henüz tamamlanmamış ve koordinatları hala aranmakta veya ayarlanmakta olan bir düğümdür. Ayrıca, her zaman mevcut (sıfır) çubuk üzerindedir. Gelecekte iken, tahmin edilen düğüm, bir sonraki ZigZag düğümünün tahmini seviyesini göstermelidir.
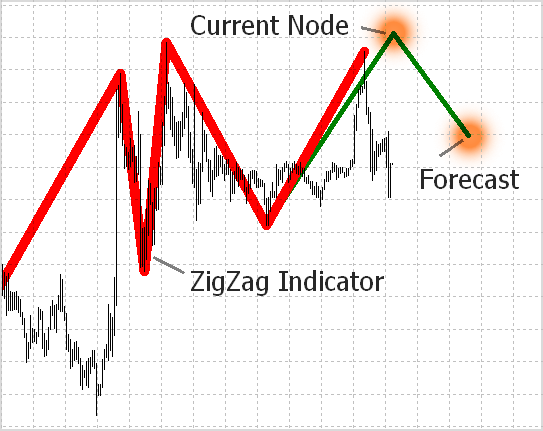
Şekil 1. Yeni ZigZag düğümlerini tahmin etme: mevcut düğüm ve sonraki düğüm.
Yan hedef belirlendi ve gelişmiş bir gösterge oluşturmak için temel olarak Hareketli Ortalama Zarflarını nasıl kullanacağımıza dair artık bir fikrimiz var (Şekil 2). ZigZag düğümlerinden sapması minimum olan zarfları arayacağız. ZigZag tepeleri ve dipleri için zarfların ayrı ayrı aranması oldukça mantıklı görünüyor.
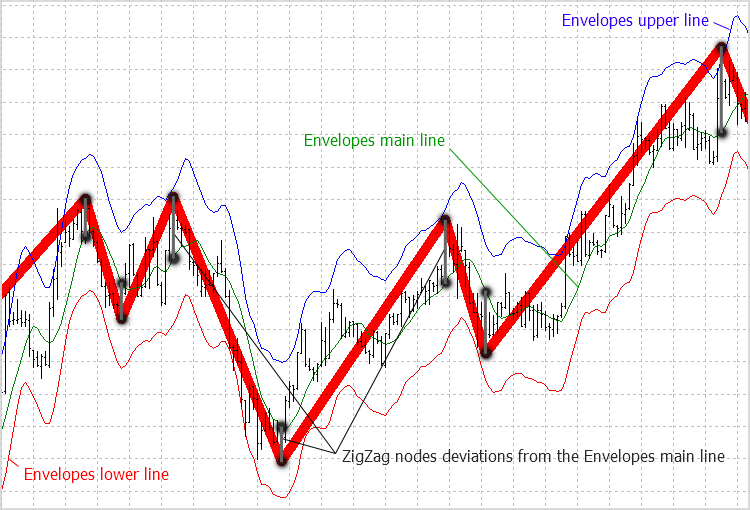
Şekil 2. ZigZag göstergeleri ve Hareketli Ortalama Zarfları.
Tahminin istatistiksel anlamlılığını artırmak için, yalnızca bir veya 10 Zarf göstergesi kullanmak yerine, farklı giriş verilerine sahip 100 veya daha fazla göstergeden oluşan bir havuz kullanmalıyız. Bunlar, ana gösterge çizgisinin ortalama dönemi ve kullanılan fiyat (tepeler için Yüksek ve dipler için Düşük) bakımından farklılık gösterir. Aşağıdaki gösterimleri ve formülleri tanıtalım:
- ZZ - ZigZag göstergesi;
- ENV - Zarflar göstergesinin ana çizgisi (iMA göstergesi ile kesişir);
- Envelopes(i) - i'inci çubuk üzerindeki Zarf göstergesinin ana çizgi değeri;
- ZZ(High) - ZigZag tepe değeri;
- ZZ(Low) - ZigZag dip değeri;
- ENV(High) - bir ZigZag tepesine karşılık gelen Zarf göstergesinin ana çizgi değeri;
- ENV(Low) - bir ZigZag dibine karşılık gelen Zarf göstergesinin ana çizgi değeri;
- n_high - ZigZag tepeleri;
- n_low - ZigZag dipleri sayısı.
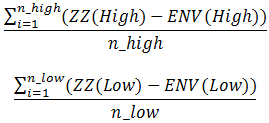
İki gösterge havuzumuz var: biri tepeler ve diğeri dipler için (her birinde yaklaşık 100 gösterge). Havuzdaki her gösterge için Zarf göstergesinin ana çizgisinden ZigZag düğümlerinin sapmasını hesaplayacağız ve yukarıdaki formülleri kullanarak her bir havuz göstergesi için sapmaların aritmetik ortalamasını bulacağız. Aşağıdaki şekil, bir gösterge için ENV ana çizgisinden tanımlanan ZZ düğümlerine göre sapmaların bir diyagramını gösterir.
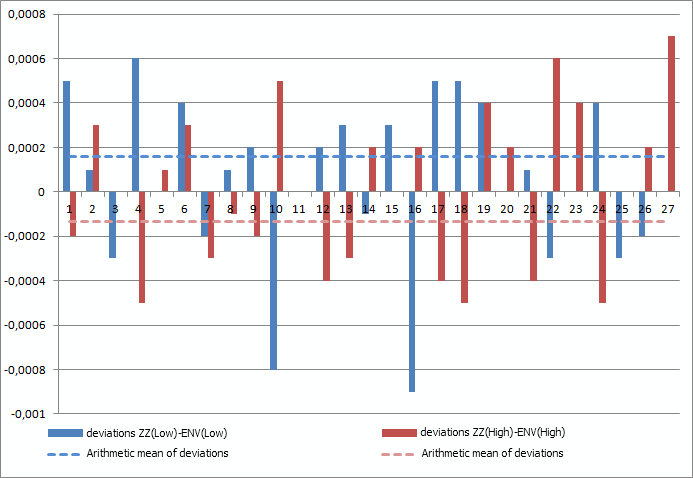
Şekil 3. ZZ düğümlerinin ENV'den sapmalarının diyagramı.
Sapmaların aritmetik ortalaması, zarf bantlarını çizmek için Zarflar göstergesinin ana çizgisinin hareket ettirilmesi gereken seviyeyi belirlemek için kullanılacaktır. Bu nedenle, Zarflar göstergesinin üst çizgisini çizmek için ZigZag tepe noktalarından sapmaların aritmetik ortalamasına ve Zarflar göstergesinin alt çizgisini çizmek için diplerden sapmaların aritmetik ortalamasına ihtiyacımız olacak.
Bunlar, karakteristik noktaları bulmak ve ZigZag düğümlerini tahmin etmek için kullanacağımız üst ve alt zarf çizgileridir. Bir kez daha belirtmeliyim:, Zarflar göstergelerinin bir kümesinden oluşan bir zarf havuzuyla ilgileniyoruz. ZigZag düğümlerinin belirli bir zarfın ana çizgisinden sapmalarının aritmetik ortalaması, her bir gösterge için hesaplanır. Havuzun ortaya çıkan çizgilerini (üst ve alt çizgi) grafiğe yerleştirdikten sonra aşağıdakileri görebiliriz:
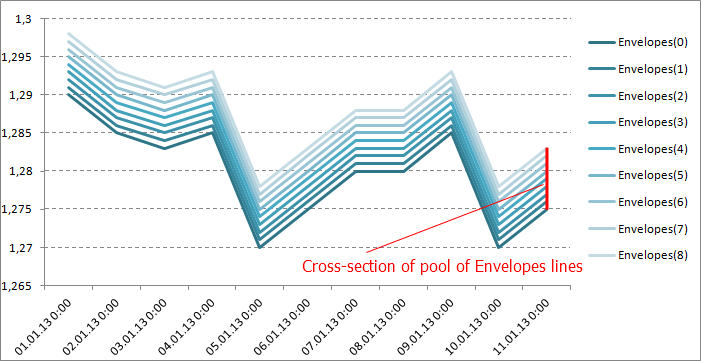
Şekil 4. Düzlem üzerindeki Zarflar çizgileri.
Her bir çizginin ayrı bir düzlemde uzandığını ve hepsinin birlikte bir yüzey oluşturduğunu varsayarsak, yukarıdaki şekil sadece her bir göstergenin fiyat grafiği düzlemindeki izdüşümünü gösterir. Bu çizgilerin bir 3B görüntüsü kabaca aşağıdaki gibi olacaktır:
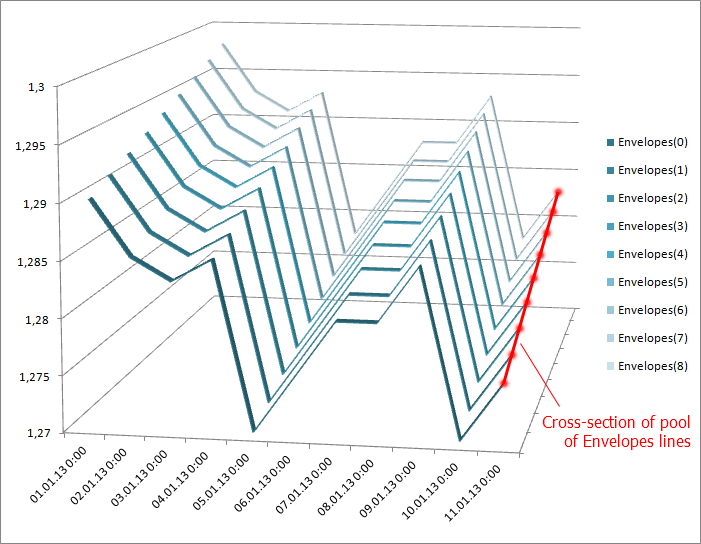
Şekil 5. 3D'de Zarflar çizgileri.
Şimdi hızlı bir geometri dersi verelim. Zarflar göstergesinin çizgi havuzunun 3B bir yüzey olduğunu hayal edelim. Fiyat grafiğine dik bir düzlem alın ve yüzeyi mevcut (sıfır) çubukta kesin.
Bunun sonucunda, bir eğriyi temsil eden yüzeyin bir kesitini elde ederiz (yukarıdaki şekiller eğrinin düz bir çizgi olduğu özel bir durumu göstermektedir). Tahminde bulunmak için, hesaplamalarda daha sonra kullanılacak olan eğri üzerindeki her noktanın koordinatlarına sahip olmak yeterlidir.
Aşağıdaki kesit özelliklerine ihtiyacımız olacak: maksimum ve minimum nokta ve kesitin ağırlık merkezi (tüm nokta değerlerinin aritmetik ortalaması). Elde edilen karakteristik noktalar, ilgili veriler geçmişe kaydedilerek mevcut (sıfır) çubuğa yansıtılacaktır. Bu karakteristik noktalar, mevcut ve sonraki ZigZag düğümleri için temel teşkil edecektir.
Zarf bantlarının aranması tepeler ve dipler için ayrı ayrı yapıldığından, sonuç olarak iki kesit almalıyız: biri tepeler için, diğeri dipler için.
Tahmini elde etmek için en yakın karakteristik noktayı kullanacağız. Örneğin, bir ZigZag tepe noktası ararken, Zarflar göstergesinin üst çizgilerinin yüzeyinin bir kesme düzlemi ile kesişmesinden kaynaklanan kesitin karakteristik noktalarını alırız. Tam tersine, bir dip noktası bulmak için, Zarflar göstergesinin alt çizgilerinin yüzeyinin bir kesme düzlemi ile kesişmesinden kaynaklanan enine kesitin karakteristik noktalarını alırız.
Yeni Göstergeyi Test Etme
Yöntemi tanımladığımıza göre şimdi göstergeyi oluşturalım. ilk olarak ZigZag göstergesinin son düğümlerini bulacağız ve bunları grafiğe çizeceğiz. Bunun için, elimizdeki iş için yazılmış AdvancedZigZag sınıfını kullanacağız:
//+------------------------------------------------------------------+ //| AdvancedZigZag.mqh | //| Copyright 2013, DC2008 | //| https://www.mql5.com/ru/users/DC2008 | //+------------------------------------------------------------------+ #property copyright "Copyright 2013, DC2008" #property link "https://www.mql5.com/ru/users/DC2008" #property version "1.00" //+------------------------------------------------------------------+ //| GetExtremums.mqh | //+------------------------------------------------------------------+ #include <GetExtremums.mqh> // author of the code Yurich #property copyright "Copyright 2012, Yurich" #property link "https://www.mql5.com/ru/users/Yurich" //+------------------------------------------------------------------+ //| ZigZag node structure | //+------------------------------------------------------------------+ struct MqlZigZag { double price; // Node coordinate datetime t; // Time }; //+------------------------------------------------------------------+ //| The AdvancedZigZag class | //+------------------------------------------------------------------+ class AdvancedZigZag { private: MqlRates rt[]; dextremum zz[]; int history; double amplitude; public: dextremum zHL[]; MqlZigZag zzH[],zzL[]; int Count(const double range); int Read(const int nodes); AdvancedZigZag(const int bars); ~AdvancedZigZag(); }; //+------------------------------------------------------------------+ //| Class constructor | //+------------------------------------------------------------------+ AdvancedZigZag::AdvancedZigZag(const int bars) { history=bars; amplitude=0; } //+------------------------------------------------------------------+ //| The Read method of the class | //+------------------------------------------------------------------+ int AdvancedZigZag::Read(const int nodes) { CopyRates(NULL,0,TimeCurrent(),history,rt); int cnt=GetExtremums(amplitude,rt,zHL,nodes); return(cnt); } //+------------------------------------------------------------------+ //| The Count method of the class | //+------------------------------------------------------------------+ int AdvancedZigZag::Count(const double range) { amplitude=range; CopyRates(NULL,0,TimeCurrent(),history,rt); int cnt=GetExtremums(amplitude,rt,zz); ArrayResize(zzH,cnt); ArrayResize(zzL,cnt); int h=0; int l=0; for(int i=0; i<cnt; i++) { if(zz[i].type>0) { zzH[h]=(MqlZigZag)zz[i]; h++; } else { zzL[l]=(MqlZigZag)zz[i]; l++; } } ArrayResize(zzH,h); ArrayResize(zzL,l); return(cnt); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ AdvancedZigZag::~AdvancedZigZag() { }
Toplamda iki yöntem vardır:
- Sayma yöntemi, belirli bir zaman dönemindeki tüm ZigZag düğümlerini (çubuk sayısı) bulur ve bunları tepeleri diplerden ayırarak çeşitli dizilerde kaydeder. Zarfların analizini ve hesaplamasını yapmak bu şekilde daha kolay olacaktır;
- Okuma yöntemi ise, son düğümleri bulur ve bunları tek bir diziye kaydeder. ZigZag gösterge görselleştirmesi için bu yönteme ihtiyacımız var;
GetExtremums kitaplığı (Yury Kulikov) de düğümlerin aranmasında gerekli olacaktır.
Bir Uzman Danışmanda göstergeyi değerlendirmeye alalım. Neden bir gösterge değil de Uzman Danışman? Bu tabii ki zevk meselesi, ama böylesi bana daha verimli geliyor. Uzman Danışmanın grafik özellikleri kuşkusuz daha zayıf, ancak her EA kendi ayrı akışında çalışırken aynı sembollü göstergeler tek bir akışta çalıştığından performans kazanırız. Koda bir bakalım:
//+------------------------------------------------------------------+ //| two_Comets.mq5 | //| Copyright 2013, DC2008 | //| https://www.mql5.com/ru/users/DC2008 | //+------------------------------------------------------------------+ #property copyright "Copyright 2013, DC2008" #property link "https://www.mql5.com/ru/users/DC2008" #property version "1.00" #include <AdvancedZigZag.mqh> //--- Depth of history for the indicator calculation input int depth_stories=5000; // Depth stories for calculating the indicator [bars] //--- Minimum ZigZag amplitude value input int amplitude=100; // The minimum value of the amplitude of the indicator [points] //--- Declaring the class AdvancedZigZag Azz(depth_stories); //--- #define NUMBER_MA 227 #define START_MA 5 //--- macros #define SIZE(i) (double)i*0.3<1?1:(int)(i*0.25) #define ObjF1 ObjectSetString(0,name,OBJPROP_FONT,"Wingdings") #define ObjF2 ObjectSetInteger(0,name,OBJPROP_ANCHOR,ANCHOR_CENTER) #define ObjF3(T) ObjectSetInteger(0,name,OBJPROP_TIME,T) #define ObjF4(P) ObjectSetDouble(0,name,OBJPROP_PRICE,P) #define ObjF5(size) ObjectSetInteger(0,name,OBJPROP_FONTSIZE,size) #define ObjF6(code) ObjectSetString(0,name,OBJPROP_TEXT,CharToString(code)) #define ObjF7(clr) ObjectSetInteger(0,name,OBJPROP_COLOR,clr) #define ObjF8 ObjectSetInteger(0,name,OBJPROP_COLOR,clrMagenta) #define ObjF9 ObjectSetInteger(0,name,OBJPROP_WIDTH,3) #define ObjF10 ObjectSetInteger(0,name,OBJPROP_BACK,true) #define ObjFont ObjF1;ObjF2; #define ObjCoordinates(T,P) ObjF3(T);ObjF4(P); #define ObjProperty(size,code,clr) ObjF5(size);ObjF6(code);ObjF7(clr); #define ObjZZ ObjF8;ObjF9;ObjF10; //--- double MA[1],sumHi[NUMBER_MA],sumLo[NUMBER_MA]; int handle_MA_H[NUMBER_MA],handle_MA_L[NUMBER_MA]; datetime t[1]; int H,L; int t_min,t_max; int err=-1; double sumH[2],maxH[2],minH[2]; double sumL[2],maxL[2],minL[2]; string name; int count; int shift; //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { shift=PeriodSeconds()/30; //--- calculation of ZigZag nodes using historical data Azz.Count(amplitude*Point()); H=ArraySize(Azz.zzH); L=ArraySize(Azz.zzL); if(H<30 || L<30) { Print("Not enough data to calculate ZigZag nodes: "+ "increase the depth of history; "+ "or decrease the amplitude value."); return(-1); } //--- for(int i=0; i<NUMBER_MA; i++) { handle_MA_H[i]=iMA(NULL,0,i+START_MA,0,MODE_SMA,PRICE_HIGH); handle_MA_L[i]=iMA(NULL,0,i+START_MA,0,MODE_SMA,PRICE_LOW); } //--- return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { ObjectsDeleteAll(0,-1,-1); for(int i=0; i<NUMBER_MA; i++) { IndicatorRelease(handle_MA_H[i]); IndicatorRelease(handle_MA_L[i]); } //--- } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- get the current bar's opening time value CopyTime(NULL,0,0,1,t); //--- ZigZag: last 7 nodes count=Azz.Read(7); for(int i=1; i<count; i++) { name="ZZ"+(string)i; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjectSetInteger(0,name,OBJPROP_COLOR,clrRed); ObjectSetInteger(0,name,OBJPROP_WIDTH,10); ObjectSetInteger(0,name,OBJPROP_BACK,true); ObjectSetDouble(0,name,OBJPROP_PRICE,0,Azz.zHL[i-1].value); ObjectSetInteger(0,name,OBJPROP_TIME,0,Azz.zHL[i-1].time); ObjectSetDouble(0,name,OBJPROP_PRICE,1,Azz.zHL[i].value); ObjectSetInteger(0,name,OBJPROP_TIME,1,Azz.zHL[i].time); } //--- check for integrity of preliminary calculations if(err<0) { //--- calculate the sums of deviations of the nodes from MA for ZigZag peaks ArrayInitialize(sumHi,0.0); for(int j=H-1; j>=0; j--) { for(int i=0; i<NUMBER_MA; i++) { err=CopyBuffer(handle_MA_H[i],0,Azz.zzH[j].t,1,MA); if(err<0) return; sumHi[i]+=Azz.zzH[j].price-MA[0]; } } //--- calculate the sums of deviations of the nodes from MA for ZigZag troughs ArrayInitialize(sumLo,0.0); for(int j=L-1; j>=0; j--) { for(int i=0; i<NUMBER_MA; i++) { err=CopyBuffer(handle_MA_L[i],0,Azz.zzL[j].t,1,MA); if(err<0) return; sumLo[i]+=MA[0]-Azz.zzL[j].price; } } } } //+------------------------------------------------------------------+
Burada birkaç şeyi açıklığa kavuşturmamız gerekiyor:
- iEnvelopes göstergesi iMA göstergesi ile değiştirilir. Burada yanlış veya yanıltıcı hiçbir şey yok. Konu, iEnvelopes ana çizgisinin iMA ile kesişmesidir! Dolayısıyla, Hareketli Ortalama göstergesini kullanmak daha uygundur.
- Her biri 227 çizgiden oluşan iki hareketli ortalamalar havuzu kullanarak toplamda 454 iMA göstergesi elde ederiz! Bu çok mu yoksa az mı? Temel olarak, bu büyük bir sayıdır. Ancak, her şeyden önce, gerekirse göstergelerin sayısını değiştirebiliriz ve ikincisi bize istatistik lazım. Bir düzine düğüm için zarf aramanın mantığı ne? En az yüz adede ihtiyacımız var.
- Gösterge değerleri OnInit() yerine OnTick() bloğuna yüklenir. Veri yükleme bloğu OnInit()'e yerleştirilirse, bazı verilerin yüklenmesi gecikebilir ve bunun sonucunda göstergeler doğru ve tam olarak hesaplanmayacaktır. Hesaplamalar için tüm veriler elde edilmesinden sonra, err değişkeni değeri pozitif olacak ve bu blok işlemden çıkarılacaktır.
Böylece, ortaya çıkan gösterge, son yedi ZigZag düğümünü çizer ve belirli bir geçmişteki diğer tüm düğümlerin koordinatlarını hesaplar (Şekil 6). Hesaplama yalnızca bir kez yapılır ve hesaplanan verileri daha sonra kullanırız. Elbette bunu, verilerin düzenli olarak güncellenmesine izin verecek şekilde uygulayabilirsiniz, ancak bu makalede bunu tek geçişle sınırlı tutacağız.
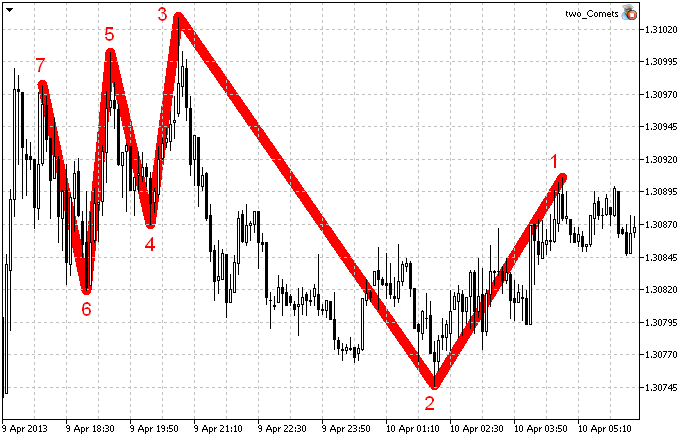
Şekil 6. ZigZag göstergesi (7 düğüm).
Ayrıca, Zarf göstergelerinin yüzeylerinin kesitlerini çizelim. Bunun için, OnTick() yöntemine aşağıdakileri ekleyeceğiz:
//--- PEAKS sumH[0]=0.0; maxH[0]=0.0; minH[0]=0.0; for(int i=0; i<NUMBER_MA; i++) { CopyBuffer(handle_MA_H[i],0,t[0],1,MA); double envelope=MA[0]+sumHi[i]/H; if(i==0 || envelope<minH[0]) { minH[0]=envelope; t_min=SIZE(i); } if(envelope>maxH[0]) { maxH[0]=envelope; t_max=SIZE(i); } sumH[0]+=envelope; name="H"+(string)i; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0]-(NUMBER_MA-i*2)*shift,envelope) ObjProperty(SIZE(i),158,clrBlue) } //--- TROUGHS sumL[0]=0.0; maxL[0]=0.0; minL[0]=0.0; for(int i=0; i<NUMBER_MA; i++) { CopyBuffer(handle_MA_L[i],0,t[0],1,MA); double envelope=MA[0]-sumLo[i]/L; if(i==0 || envelope<minL[0]) { minL[0]=envelope; t_min=SIZE(i); } if(envelope>maxL[0]) { maxL[0]=envelope; t_max=SIZE(i); } sumL[0]+=envelope; name="L"+(string)i; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0]+(NUMBER_MA-i*2)*shift,envelope) ObjProperty(SIZE(i),158,clrGold) }
Zarf çizgilerinin oluşturduğu yüzeyin kesit noktalarını ayırt etmek için, noktaların boyutu değişiklik gösterir: Zarflar göstergelerinin ana çizgisinin ortalama dönemi ne kadar büyükse, noktalar o kadar büyük olur (Şekil 7). Ayrıca kesitler, mevcut (sıfır) çubuğun içinden farklı yönlerde geçen dikey bir eksen etrafında döndürülür: tepe noktaları 90 derece sağa ve dipler 90 derece sola.
Artık bunlar, fiyat grafiği düzleminde görüntülenebilir. Başlangıçta kesme düzleminde bulunuyorlardı (Şekil 5) ve gözlenememişlerdi. Şekilleri hakkında hiçbir fikrimiz olmadan onları sadece kendimizce hayal edebiliyorduk. Kesit çizgileri çok tuhaf bir şekle sahip olduğu ortaya çıktı. Bu aynı zamanda grafik analiz kolaylığı için yapılır. Görsel olarak kesitler iki uçan kuyruklu yıldıza benziyor:
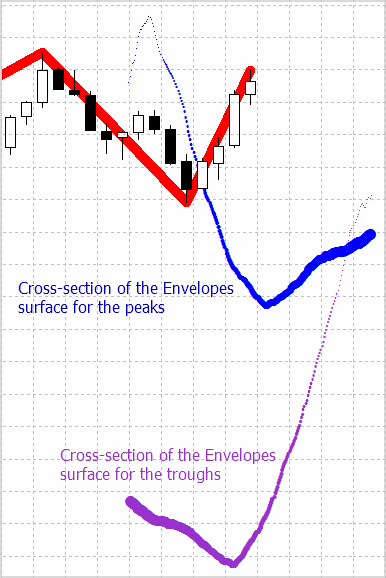
Şekil 7. Zarflar gösterge havuzunun kesiti.
Kesit karakteristiklerinin hesaplanmasına geçelim: maksimum ve minimum ve ağırlık merkezi (aritmetik ortalama). Ortaya çıkan değerler, ilgili karakteristik boyutuna karşılık gelen nokta boyutu ile mevcut çubuk üzerinde noktalar olarak görüntülenecektir. Ek olarak, daha fazla analiz için bunları geçmişe kaydedeceğiz. Bu nedenle, mevcut koda aşağıdakileri ekleyeceğiz:
//--- PEAKS ... //--- midi string str=(string)t[0]; name="Hmidi"+str; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0],sumH[0]/NUMBER_MA) ObjProperty(10,119,clrBlue) //--- max name="Hmax"+str; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0],maxH[0]) ObjProperty(t_max,158,clrBlue) //--- min name="Hmin"+str; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0],minH[0]) ObjProperty(t_min,158,clrBlue) ... //--- TROUGHS ... //--- midi name="Lmidi"+str; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0],sumL[0]/NUMBER_MA) ObjProperty(10,119,clrGold) //--- max name="Lmax"+str; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0],maxL[0]) ObjProperty(t_max,158,clrGold) //--- min name="Lmin"+str; ObjectCreate(0,name,OBJ_TEXT,0,0,0); ObjFont ObjCoordinates(t[0],minL[0]) ObjProperty(t_min,158,clrGold)
Şimdi grafiksel olarak temsil edildiğinde neye benzediğini görelim:
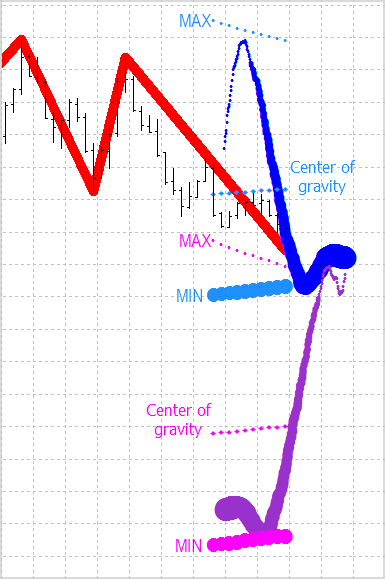
Şekil 8. Kesit karakteristikleri: maksimum ve minimum ve tepe ve dipler için ayrı ayrı çizilen ağırlık merkezi.
Gelişmiş ZigZag düğümlerini bulup çizerek son dokunuşu eklememiz yeterli. Aşağıdakileri ekleyerek kodu geliştiriyoruz:
//--- ZigZag: advanced nodes if(Azz.zHL[0].type>0) // peak { ObjectDelete(0,"MIN"); ObjectDelete(0,"MINfuture"); name="MAX"; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjZZ ObjectSetDouble(0,name,OBJPROP_PRICE,0,Azz.zHL[1].value); ObjectSetInteger(0,name,OBJPROP_TIME,0,Azz.zHL[1].time); ObjectSetInteger(0,name,OBJPROP_TIME,1,t[0]); double price=minH[0]; ObjectSetDouble(0,name,OBJPROP_PRICE,1,price); if(Azz.zHL[0].value>minH[0]) { price=sumH[0]/NUMBER_MA; ObjectSetDouble(0,name,OBJPROP_PRICE,1,price); } if(Azz.zHL[0].value>sumH[0]/NUMBER_MA) { price=maxH[0]; ObjectSetDouble(0,name,OBJPROP_PRICE,1,price); } //--- into the future name="MAXfuture"; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjZZ ObjectSetDouble(0,name,OBJPROP_PRICE,0,price); ObjectSetInteger(0,name,OBJPROP_TIME,0,t[0]); ObjectSetDouble(0,name,OBJPROP_PRICE,1,maxL[0]); ObjectSetInteger(0,name,OBJPROP_TIME,1,t[0]+NUMBER_MA*shift); if(price<maxL[0]) ObjectSetDouble(0,name,OBJPROP_PRICE,1,sumL[0]/NUMBER_MA); if(price<sumL[0]/NUMBER_MA) ObjectSetDouble(0,name,OBJPROP_PRICE,1,minL[0]); } if(Azz.zHL[0].type<0) // trough { ObjectDelete(0,"MAX"); ObjectDelete(0,"MAXfuture"); name="MIN"; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjZZ ObjectSetDouble(0,name,OBJPROP_PRICE,0,Azz.zHL[1].value); ObjectSetInteger(0,name,OBJPROP_TIME,0,Azz.zHL[1].time); ObjectSetInteger(0,name,OBJPROP_TIME,1,t[0]); double price=maxL[0]; ObjectSetDouble(0,name,OBJPROP_PRICE,1,price); if(Azz.zHL[0].value<maxL[0]) { price=sumL[0]/NUMBER_MA; ObjectSetDouble(0,name,OBJPROP_PRICE,1,price); } if(Azz.zHL[0].value<sumL[0]/NUMBER_MA) { price=minL[0]; ObjectSetDouble(0,name,OBJPROP_PRICE,1,price); } //--- into the future name="MINfuture"; ObjectCreate(0,name,OBJ_TREND,0,0,0); ObjZZ ObjectSetDouble(0,name,OBJPROP_PRICE,0,price); ObjectSetInteger(0,name,OBJPROP_TIME,0,t[0]); ObjectSetDouble(0,name,OBJPROP_PRICE,1,minH[0]); ObjectSetInteger(0,name,OBJPROP_TIME,1,t[0]+NUMBER_MA*shift); if(price>minH[0]) ObjectSetDouble(0,name,OBJPROP_PRICE,1,sumH[0]/NUMBER_MA); if(price>sumH[0]/NUMBER_MA) ObjectSetDouble(0,name,OBJPROP_PRICE,1,maxH[0]); }
Böylece, yeni düğümlerin pozisyonunu tahmin eden yeni gelişmiş ZigZag göstergemiz oluyor (Şekil 9). Düğümlerin kendileri karakteristik kesit noktalarında bulunur: maksimum, minimum ve ağırlık merkezi. Göstergenin çalışma başlığı "İki Kuyruklu Yıldız"dır.
Gelecekte olan bir sonraki düğümün tamamlanma süresinin belirsiz kaldığı unutulmamalıdır. Temel olarak, yalnızca bir düğüm koordinatını tahmin edebiliriz, o da fiyattır.
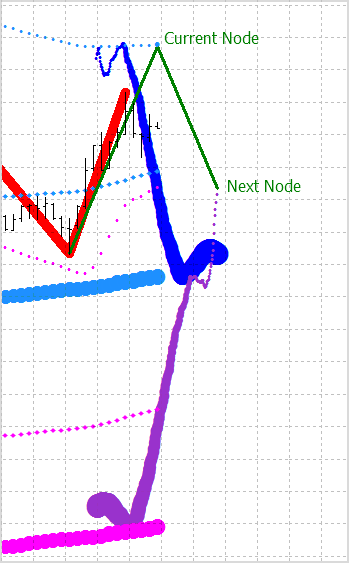
Şekil 9. Gelişmiş ZigZag göstergesi şu düğümleri tahmin eder: mevcut ve sonraki.
Sonuçların Analiz ve Geliştiriciler için Tavsiyeler
Gösterge gözlemleri şunları göstermiştir:
- ZigZag düğüm koordinatlarının tahmin edilen düğümlerden sapmaları tolerans bölgesi dahilindedir. Çok sayıda düğüm, ilgili kesitin gölgesinde yer almaktadır. Bu mutlak surette yalnızca nitel bir değerlendirmedir. Sonraki makalelerde daha doğru sonuçlar gelecektir.
- Zarf çizgilerinin kesitleri, piyasa davranışını ve beklenen fiyat momentumunu gösterir! En küçük (boyut olarak en küçük) ortalama döneme sahip noktalardan oluşan kuyruklu yıldız kuyruğuna dikkat edin. Bu, fiyat yönünde yönlendirilir. Kuyruklu yıldızın kuyruğu en karmaşık şekillerde bükülür ve ters yöne ne kadar çok döndürülürse, trend değişikliğini görme şansı o kadar artar. Sadece göstergenin davranışını farklı büyüklüklere sahip farklı zaman aralıklarında izleyin. Bu son derece ilginç!
- Kesitlerin karakteristik noktaları, fiyat hareketine karşı güçlü direnç gösterebilecek çizgiler oluşturur. Bu nedenle bunlar, destek ve direnç çizgileri olarak kabul edilebilir.
- Kesitin ağırlık merkezi noktaları bunun önüne geçtiğinde (Şekil 9'daki tepeler gibi), bu, yukarı doğru trend varlığının bir göstergesidir.
Böylelikle, bir alım satım stratejisinde denenebilecek çok ilginç bir gösterge elde ettik!
Sonuç
- Makalede incelenen ZigZag gösterge düğümlerini tahmin etme yöntemi, yeni gösterge olan "İki Kuyruklu Yıldız" oluşturmamıza olanak sağlamıştır.
- Gelişmiş ZigZag yeni düğümlerin olası koordinatlarını göstermekle birlikte yalnızca bir tahmindir.
- Makalede ele alınan algoritma, mutlaka ZigZag göstergeleri olmak zorunda olmaksızın, örneğin fraktallar veya semafor göstergeleri gibi benzer gelişmiş göstergeleri çizmek için kullanılabilir.
- Acemi MQL5 programcıları, tekrarlanan kod miktarını azaltmak için programlarında nasıl makro oluşturabileceklerini görmeyi ilginç bulabilir.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/646
MQL5 Tarif Defteri: Üçlü Ekran Stratejisine Dayalı Bir Alım Satım Sistemi Çerçevesi Geliştirme
MQL5 Tarif Defteri: Uzman Danışmanlarda Alım Satım Koşullarını Belirlemek için Göstergeleri Kullanma
MQL5 Tarif Defteri: Çok Para Birimli Uzman Danışman - Basit, Sade ve Hızlı Yaklaşım
MQL5 Tarif Defteri: Pozisyon Özelliklerini Elde Etmek için İşlemler Geçmişi ve Fonksiyon Kitaplığı
- Ücretsiz ticaret uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz