Model aramada brute force yaklaşımı (Bölüm VI): Döngüsel optimizasyon

İçindekiler

• Giriş
• Rutin
• Yeni optimizasyon algoritması
• En önemli optimizasyon kriteri
• Alım-satım konfigürasyonları için otomatik arama
• Sonuç
• Linkler

Giriş

Bir önceki makalemdeki materyaller göz önüne alındığında, bunun algoritmama eklediğim tüm işlevlerin sadece yüzeysel bir açıklaması olduğunu söyleyebilirim. Bunlar sadece Uzman Danışman oluşturmanın tam otomasyonu ile ilgili değil, aynı zamanda optimizasyonun ve otomatik alım-satım için daha sonra kullanılacak sonuçların seçiminin tam otomasyonu veya biraz sonra göstereceğim daha kapsamlı Uzman Danışmanların oluşturulması gibi önemli işlevlerle de ilgilidir.

İşlem terminallerinin, evrensel Uzman Danışmanların ve algoritmanın kendisinin ortak yaşamı sayesinde, manuel geliştirmeden tamamen kurtulabilir veya en kötü durumda, gerekli hesaplama yeteneklerine sahip olmanız koşuluyla, olası iyileştirmeler için harcayacağınız emeği büyük ölçüde azaltabilirsiniz. Bu makalede, bu yeniliklerin en önemli yönlerini anlatmaya başlayacağım.

Rutin

Benim için bu tür çözümlerin oluşturulmasında ve zaman içinde değiştirilmesinde en önemli faktör, rutin eylemlerin maksimum otomasyonunu sağlama olasılığını anlamaktı. Bu durumda rutin eylemler, gerekli olmayan tüm insan çalışmalarını içerir:

• Fikir üretme.
• Teori oluşturma.
• Teoriye göre kod yazma.
• Kodu düzeltme.
• Sürekli Uzman Danışman yeniden optimizasyonu.
• Sabit Uzman Danışman seçimi.
• Uzman Danışman bakımı.
• Terminallerle çalışma.
• Deneyler ve uygulama.
• Diğer.

Gördüğünüz gibi, bu rutinin kapsamı oldukça geniştir. Bunu tam olarak bir rutin olarak ele alıyorum, çünkü tüm bu şeylerin otomatikleştirilebileceğini kanıtlayabildim. Genel bir liste sundum. Kim olduğunuz önemli değil - bir algoritmik yatırımcı, bir programcı veya her ikisi de. Programlamayı bilip bilmemeniz önemli değil. Bilmeseniz bile, her durumda bu listenin en az yarısıyla karşılaşacaksınız. Mağazadan bir Uzman Danışman satın aldığınız, onu grafikte başlattığınız ve tek bir düğmeye basarak sakinleştiğiniz durumlardan bahsetmiyorum. Bu elbette çok nadiren de olsa gerçekleşmektedir.

Tüm bunları anladıktan sonra, öncelikle en belirgin şeyleri otomatikleştirmem gerekiyordu. Tüm bu optimizasyonu daha önceki bir makalede kavramsal olarak tanımlamıştım. Ancak, böyle bir şey yaptığınızda, halihazırda uygulanan işlevselliğe dayanarak her şeyi nasıl iyileştirebileceğinizi anlamaya başlarsınız. Benim için bu konudaki ana fikirler şunlardı:

• Optimizasyon mekanizmasının iyileştirilmesi.
• Uzman Danışmanları birleştirmek için bir mekanizma oluşturulması (botları birleştirme).
• Tüm bileşenlerin etkileşim yollarının doğru mimarisi.

Elbette bu oldukça kısa bir sıralamadır. Her şeyi daha ayrıntılı olarak anlatacağım. Optimizasyonu iyileştirmek derken, aynı anda birkaç faktörün bir araya gelmesini kastediyorum. Tüm bunlar, tüm sistemi inşa etmek için seçilen paradigma içinde düşünülmüştür:

• Tikleri ortadan kaldırarak optimizasyonu hızlandırmak.
• Alım-satım karar noktaları arasındaki kar eğrisi kontrolünü ortadan kaldırarak optimizasyonu hızlandırmak.
• Özel optimizasyon kriterleri getirerek optimizasyon kalitesini artırmak.
• İleri dönem verimliliğini maksimize etmek.

Bu web sitesinin Forumunda, optimizasyonun gerekli olup olmadığı ve faydalarının neler olduğu ile ilgili hala devam eden tartışmaları bulabilirsiniz. Daha önce, büyük ölçüde bireysel forum ve web sitesi kullanıcılarının etkisi nedeniyle bu konuya karşı oldukça net bir tavrım vardı. Şimdi bu görüş beni hiç rahatsız etmiyor. Her şey optimizasyonu nasıl doğru kullanacağınızı bilip bilmediğinize ve hedeflerinizin ne olduğuna bağlıdır. Doğru kullanıldığında optimizasyon istenen sonucu verir. Genel olarak, optimizasyonun son derece faydalı olduğu ortaya çıkıyor.

Birçok kişi optimizasyonu sevmez. Bunun iki objektif nedeni vardır:

• Temel bilgilerin anlaşılmaması (neden, ne ve nasıl yapılacağı, sonuçların nasıl seçileceği ve deneyim eksikliği de dahil olmak üzere bununla ilgili her şey).
• Optimizasyon algoritmalarının kusurluluğu.

Aslında her iki faktör de birbirini güçlendirmektedir. Adil olmak gerekirse, MetaTrader 5 optimizasyon aracının yapısal olarak kusursuz olduğunu söylemek isterim, ancak optimizasyon kriterleri ve olası filtreler açısından hala birçok iyileştirmeye ihtiyacı var. Şimdiye kadar, tüm bu işlevsellik çocukların kum havuzuna benziyor. Çok az insan pozitif ileri dönemlere nasıl ulaşılacağını ve en önemlisi bu sürecin nasıl kontrol edileceğini düşünür. Ben bu konu üzerinde uzun zamandır düşünüyorum. Aslında bu makalenin büyük bir bölümü bu konuya ayrılacaktır.

Yeni optimizasyon algoritması

Herhangi bir geriye dönük testin bilinen temel değerlendirme kriterlerine ek olarak, sonuçların daha verimli seçilmesi ve ayarların daha sonra uygulanması için herhangi bir algoritmanın değerini katlamaya yardımcı olabilecek bazı birleşik özellikler bulabiliriz. Bu özelliklerin avantajı, çalışan ayarları bulma sürecini hızlandırabilmeleridir. Bunu yapmak için, MetaTrader'dakine benzer bir tür strateji sınayıcı oluşturdum:

Şekil 1

Bu araç sayesinde tek bir tıklamayla istediğim seçeneği seçebiliyorum. Tıkladığımda, hemen alıp terminaldeki uygun klasöre taşıyabileceğim bir ayar oluşturulur, böylece evrensel Uzman Danışmanlar onu okuyabilir ve üzerinde işlem yapmaya başlayabilir. Ayarların doğrudan içinde bulunduğu ayrı bir Uzman Danışmana ihtiyacım olması durumunda, ilgili düğmeye tıklayarak bir Uzman Danışman oluşturabilirim. Ayrıca, tablodan bir sonraki seçenek seçildiğinde yeniden çizilen bir kar eğrisi de mevcuttur.

Tabloda nelerin dikkate alındığına bakalım. Bu özelliklerin hesaplanması için temel unsurlar aşağıdaki verilerdir:

1. Points - ilgili enstrümanın "_Point" cinsinden tüm geriye dönük test karı.
2. Orders - tamamen açık ve kapalı emirlerin sayısı ("sadece bir açık emir olabilir" kuralına göre birbirlerini kesin bir sırayla takip ederler).
3. Drawdown - bakiye düşüşü.

Bu değerlere dayanarak aşağıdaki alım-satım özellikleri hesaplanır:

• Math Waiting - puan cinsinden matematiksel beklenti.
• P Factor - [-1 ... 0 ... 1] aralığına normalize edilmiş kar faktörünün analoğu (benim kriterim).
• Martingale - martingale uygulanabilirliği (benim kriterim).
• MPM Complex - önceki üçünün bileşik bir göstergesi (benim kriterim).

Şimdi bu kriterlerin nasıl hesaplandığını görelim:

Denklemler 1

Gördüğünüz gibi, oluşturduğum tüm kriterler çok basit ve en önemlisi anlaşılması kolay. Kriterlerin her birindeki artış, geriye dönük test sonucunun olasılık teorisi açısından daha iyi olduğunu gösterdiğinden, "MPM Complex" kriterinde yaptığım gibi bu kriterleri çoğaltmak mümkün hale geliyor. Ortak bir ölçüt, sonuçları önemlerine göre daha etkili bir şekilde sıralayacaktır. Büyük çaplı optimizasyonlar durumunda, daha fazla yüksek kaliteli seçeneğin korunmasına ve daha fazla düşük kaliteli seçeneğin kaldırılmasına olanak tanır.

Ayrıca, bu hesaplamalarda her şeyin puan cinsinden gerçekleştiğini unutmayın. Bunun optimizasyon süreci üzerinde olumlu bir etkisi vardır. Hesaplamalar için, her zaman başlangıçta hesaplanan kesinlikle pozitif birincil değerler kullanılır. Geri kalan her şey bunlara göre hesaplanır. Tabloda yer almayan bu birincil değerleri listelemekte fayda olduğunu düşünüyorum:

• Points Plus - her bir karlı veya sıfır emrin puan cinsinden karlarının toplamı.
• Points Minus - her bir zarar eden emrin puan cinsinden kayıplarının (mutlağı alınarak) toplamı.
• Drawdown - bakiye düşüşü (kendi yöntemimle hesaplıyorum).

Buradaki en ilginç şey, düşüşün nasıl hesaplandığıdır. Bizim durumumuzda bu, maksimum göreceli bakiye düşüşüdür. Test algoritmamın fon eğrisini izlemeyi reddettiği gerçeği göz önüne alındığında, diğer düşüş türleri hesaplanamaz. Ancak bu düşüşü nasıl hesapladığımı göstermenin faydalı olacağını düşünüyorum:

Şekil 2

Çok basit bir şekilde tanımlanmıştır:

1. Geriye dönük testin başlangıç noktasını hesaplarız (ilk düşüş için aramanın başlangıcı).
2. Alım-satım karla başlarsa, bakiyenin büyümesini takiben ilk negatif değer görünene kadar bu noktayı yukarı doğru hareket ettiririz (ilk negatif değer, düşüş hesaplamasının başlangıcını işaret eder).
3. Bakiye referans noktası seviyesine ulaşana kadar bekleriz. Sonrasında, bunu yeni bir referans noktası olarak ayarlarız.
4. Düşüş aramasının son bölümüne geri döner ve üzerindeki en düşük noktayı buluruz (bu bölümdeki düşüş miktarı bu noktadan hesaplanır).
5. Tüm geriye dönük test veya alım-satım eğrisi için tüm süreci tekrarlarız.

Son döngü her zaman tamamlanmamış olarak kalacaktır. Ancak, söz konusu düşüş de dikkate alınır (testin devam etmesi halinde artma potansiyeli olmasına rağmen). Fakat bu, burada özellikle önemli bir husus değildir.

En önemli optimizasyon kriteri

Şimdi en önemli filtre hakkında konuşalım. Aslında bu kriter, optimizasyon sonuçlarını seçerken en önemli kriterdir. Bu kriter, MetaTrader 5 optimizasyon aracının işlevselliğine dahil edilmemiştir ki bu üzücüdür. Bu nedenle, herkesin bu algoritmayı kendi kodunda yeniden üretebilmesi için teorik materyal sağlayacağım. Aslında, bu kriter tüm alım-satım türleri için çok işlevlidir ve spor bahisi, kripto para birimi ve aklınıza gelebilecek diğer her şey dahil olmak üzere kesinlikle herhangi bir kar eğrisi için çalışır. Kriter aşağıdaki gibidir:

Denklemler 2

Bu denklemin içinde ne olduğunu görelim:

• N - tüm geriye dönük test veya alım-satım bölümü boyunca tamamen açık ve kapalı pozisyonların sayısı.
• B(i) - ilgili kapalı "i" pozisyonundan sonraki bakiye çizgisinin değeri.
• L(i) - sıfırdan bakiyenin en son noktasına (nihai bakiye) çizilen düz çizgi.

Bu parametreyi hesaplamak için iki geriye dönük test gerçekleştirmemiz gerekir. İlk geriye dönük test nihai bakiyeyi hesaplayacaktır. Bundan sonra, her bir bakiye noktasının değerini kaydeden ilgili göstergeyi hesaplamak mümkün olacak, böylece gereksiz hesaplamalar yapmaya gerek kalmayacaktır. Bununla birlikte, bu hesaplama tekrarlanan geriye dönük test olarak adlandırılabilir. Bu denklem, Uzman Danışmanlarınıza yerleştirilebilen özel sınayıcılarda kullanılabilir.

Bu göstergenin bir bütün olarak daha iyi anlaşılması için değiştirilebileceğini belirtmek önemlidir. Örneğin, şu şekilde:

Denklemler 3

Bu denklem algılama ve anlama açısından daha zordur. Ancak pratik açıdan bakıldığında böyle bir kriter uygundur çünkü ne kadar yüksek olursa bakiye eğrimiz o kadar düz bir çizgiye benzer. Daha önceki makalelerimde de benzer konulara değinmiş, ancak bunların ardındaki anlamı açıklamamıştım. İlk olarak aşağıdaki şekle bakalım:

Şekil 3

Bu şekil bir bakiye çizgisi ve iki eğri göstermektedir: eğrilerden biri bizim denklemimize (kırmızı), diğeri ise aşağıdaki değiştirilmiş kritere (Denklemler 11) ilişkindir. Bunu daha sonra göstereceğim, ancak şimdi denkleme odaklanalım.

Geriye dönük testimizi bakiyeleri olan basit bir nokta dizisi olarak hayal edersek, bunu istatistiksel bir örneklem olarak temsil edebilir ve olasılık teorisi denklemlerini uygulayabiliriz. Düz çizgiyi hedeflediğimiz model ve kar eğrisini de modelimiz için çabalayan gerçek veri akışı olarak kabul edeceğiz.

Doğrusallık faktörünün mevcut tüm alım-satım kriterleri setinin güvenilirliğini gösterdiğini anlamak önemlidir. Buna karşılık, verilerin daha yüksek güvenilirliği, olası daha uzun ve daha iyi bir ileri döneme (gelecekte karlı alım-satım) işaret edebilir. Açıkçası, başlangıçta bu tür şeyleri rastgele değişkenleri göz önünde bulundurarak değerlendirmeye başlamalıydım, ancak bana böyle bir sunumun anlaşılmasını kolaylaştırması gerektiğini düşündüm.

Olası rastgele aykırı değerleri hesaba katarak doğrusallık faktörümüzün alternatif bir benzerini oluşturalım. Bunu yapmak için, bizim için uygun bir rastgele değişken ve sonraki dağılım hesaplaması için ortalamasını tanıtmamız gerekecektir:

Denklemler 4

Daha iyi anlaşılması için, birbirini kesinlikle takip eden "N" adet tamamen açık ve kapalı pozisyonumuz olduğu netleştirilmelidir. Bu, bakiye çizgisinin bu segmentlerini bağlayan "N+1" noktamız olduğu anlamına gelir. Tüm çizgilerin sıfır noktası ortaktır, bu nedenle verileri, tıpkı son nokta gibi sonuçları iyileştirme yönünde bozacaktır. Dolayısıyla, onları hesaplamaların dışına atıyoruz ve geriye üzerinde hesaplamalar yapacağımız "N-1" nokta kalıyor.

İki çizgideki değer dizilerini bire dönüştürmek için ifade seçimi çok ilginç oldu. Lütfen aşağıdaki kesire dikkat edin:

Denklemler 5

Burada önemli olan, her durumda her şeyi nihai bakiyeye bölmemizdir. Böylece, her şeyi göreceli bir değere indirgiyoruz, bu da istisnasız tüm test edilen stratejiler için hesaplanan özelliklerin denkliğini sağlıyor. Aynı kesrin doğrusallık faktörünün ilk ve basit kriterinde de bulunması tesadüf değildir, çünkü aynı düşünce üzerine inşa edilmiştir. Alternatif kriterimizin inşasını tamamlayalım. Bunu yapmak için, dağılım gibi iyi bilinen bir kavramı kullanabiliriz:

Denklemler 6

Dağılım, tüm örneklemin ortalamasından sapmanın karesinin aritmetik ortalamasından başka bir şey değildir. İfadeleri yukarıda tanımlanmış olan rastgele değişkenlerimizi hemen yerine koydum. İdeal bir eğrinin ortalama sapması sıfırdır ve sonuç olarak belirli bir örneklemin dağılımı da sıfır olacaktır. Bu verilere dayanarak, bu dağılımın yapısı gereği (kullanılan rastgele değişken veya örneklem (dilediğiniz gibi)) alternatif bir doğrusallık faktörü olarak kullanılabileceğini tahmin etmek kolaydır. Ayrıca, örneklem parametrelerini daha etkili bir şekilde kısıtlamak için her iki kriter birlikte kullanılabilir, ancak dürüst olmak gerekirse ben sadece ilk kriteri kullanıyorum.

Şimdi de tanımladığımız yeni doğrusallık faktörüne dayanan benzer ve daha kullanışlı bir kritere bakalım:

Denklemler 7

Gördüğümüz gibi, ilk kriter temel alınarak oluşturulan benzer bir kriterle aynıdır (Denklemler 2). Ancak bu iki kriter, akla gelebileceklerin sınırından çok uzaktır. Bu düşünceyi destekleyen açık bir gerçek, bu kriterin çok idealize edilmiş olup ideal modeller için daha uygun olduğu ve bir Uzman Danışmanı az ya da çok anlamlı bir karşılık elde etmek için ayarlamanın son derece zor olacağıdır. Denklemleri uyguladıktan bir süre sonra belirginleşecek olumsuz faktörleri sıralamakta fayda olduğunu düşünüyorum:

1. İşlem sayısında kritik azalma (sonuçların güvenilirliğini azaltır)
2. Maksimum sayıda verimli senaryonun reddedilmesi (stratejiye bağlı olarak, eğri her zaman düz çizgiye yönelmez)

Bu kusurlar çok kritiktir, çünkü amaç iyi stratejileri bir kenara atmak değil, aksine bu kusurlardan arınmış yeni ve iyileştirilmiş kriterler bulmaktır. Bu dezavantajlar, her biri kabul edilebilir veya tercih edilen bir model olarak nitelendirilebilecek birkaç tercih edilen çizginin aynı anda tanıtılmasıyla tamamen veya kısmen etkisiz hale getirilebilir. Bu kusurlardan arındırılmış yeni iyileştirilmiş kriteri anlamak için sadece ilgili değişimi anlamamız gerekir:

Denklemler 8

Daha sonra listedeki her eğri için uyum faktörünü hesaplayabiliriz:

Denklemler 9

Benzer şekilde, her bir eğri için rastgele aykırı değerleri dikkate alan alternatif bir kriter de hesaplayabiliriz:

Denklemler 10

Ardından aşağıdakileri hesaplamamız gerekecektir:

Denklemler 11

Burada eğri ailesi faktörü adı verilen bir ölçüt tanıtıyorum. Aslında, böyle yaparak, eş zamanlı olarak alım-satım eğrimize en benzer eğriyi ve hemen ona karşılık gelen faktörü buluyoruz. Minimum eşleşme faktörüne sahip eğri gerçek duruma en yakın olanıdır. Değerini değiştirilmiş kriterin değeri olarak alıyoruz ve tabii ki hesaplama, iki varyasyondan hangisini daha çok sevdiğimize bağlı olarak iki şekilde yapılabilir.

Bunların hepsi çok güzel, ancak burada, birçok kişinin fark ettiği gibi, böyle bir eğri ailesinin seçimiyle ilgili nüanslar var. Böyle bir aileyi doğru bir şekilde tanımlamak için çeşitli hususlar göz önünde bulundurulabilir, ancak işte benim düşüncelerim:

• Tüm eğrilerde bükülme noktaları olmamalıdır (sonraki her ara nokta bir öncekinden kesinlikle daha yüksek olmalıdır).
• Eğri içbükey olmalıdır (eğrinin dikliği sabit olabilir ya da sadece artabilir).
• Eğrinin içbükeyliği ayarlanabilir olmalıdır (örneğin, eğilme miktarı bazı göreceli değerler veya yüzde kullanılarak ayarlanmalıdır).
• Eğri modelinin basitliği (modeli başlangıçta basit ve anlaşılabilir grafiksel modellere dayandırmak daha iyidir).

Bu, bu eğri ailesinin yalnızca ilk halidir. İstenen tüm konfigürasyonları dikkate alarak daha kapsamlı varyasyonlar yapmak mümkündür, bu da bizi kalite ayarlarını kaybetmekten tamamen kurtarabilir. Bu görevi daha sonra ele alacağım, ancak şimdilik sadece içbükey eğriler ailesinin orijinal stratejisine değineceğim. Matematik bilgimi kullanarak böyle bir aileyi oldukça kolay bir şekilde oluşturabildim. Hemen size bu eğri ailesinin nihai olarak neye benzediğini göstereyim:

Şekil 4

Böyle bir aileyi oluştururken, dikey destekler üzerinde duran elastik bir çubuk soyutlamasını kullandım. Böyle bir çubuğun eğilme derecesi, kuvvetin uygulama noktasına ve büyüklüğüne bağlıdır. Bunun burada uğraştığımız şeye sadece biraz benzediği açıktır, ancak görsel olarak benzer bir model geliştirmek için oldukça yeterlidir. Bu durumda, elbette, öncelikle geriye dönük test grafiğindeki noktalardan biriyle çakışması gereken ekstremum koordinatını belirlemeliyiz ve orada X ekseni sıfırdan başlayan işlem indeksleri ile temsil edilir. şu şekilde hesaplıyorum:

Denklemler 12

Burada iki durum söz konusudur: çift ve tek "N" için. "N" çift olursa, indeks bir tamsayı olması gerektiğinden basitçe ikiye bölmek imkansızdır. Bu arada, son şekilde tam olarak bu durumu tasvir ettim. Orada, kuvvet uygulama noktası başlangıca biraz daha yakındır. Elbette bunun tersini, biraz daha sona yakın bir şekilde yapabilirsiniz, ancak bu, şekilde gösterdiğim gibi, yalnızca az sayıda işlemle önemli olacaktır. İşlem sayısı arttıkça, tüm bunlar optimizasyon algoritmaları için önemli bir rol oynamayacaktır.

Yüzde cinsinden "P" eğilme değerini ve geriye dönük testin "B" nihai bakiyesini belirledikten sonra, daha önce ekstremum koordinatını tespit ettikten sonra, kabul edilen eğri ailesinin her biri için ifadeler oluşturmak üzere diğer bileşenleri sırayla hesaplamaya başlayabiliriz. Devamında, geriye dönük testin başlangıcını ve sonunu birleştiren düz çizginin dikliğine ihtiyacımız var:

Denklemler 13

Bu eğrilerin bir diğer özelliği de "N0" apsisinin bulunduğu noktalarda eğrilerin her birinin açı tanjantının "K" ile aynı olmasıdır. Denklemleri oluştururken, görevden bu koşulu talep ettim. Bu, son şekilde (Şekil 4) grafiksel olarak da görülebilir ve orada da bazı denklemler ve özdeşlikler vardır. Devam edelim. Şimdi aşağıdaki değeri hesaplamamız gerekiyor:

Denklemler 14

 

"P"nin ailedeki her eğri için farklı ayarlandığını unutmayın. Açıkça söylemek gerekirse, bunlar bir aileden bir eğri oluşturmak için kullanılan denklemlerdir. Bu hesaplamalar ailedeki her eğri için tekrarlanmalıdır. O zaman bir başka önemli oranı hesaplamamız gerekiyor:

Denklemler 15

Bunların anlamını irdelemeye gerek yoktur. Bunlar yalnızca eğri oluşturma sürecini basitleştirmek için oluşturulmuştur. Geriye son yardımcı oranı hesaplamak kalıyor:

Denklemler 16

Şimdi, elde edilen verilere dayanarak, oluşturulan eğrinin noktalarını hesaplamak için matematiksel bir ifade alabiliriz. Ancak, öncelikle eğrinin tek bir denklemle tanımlanmadığını açıklığa kavuşturmak gerekir. "N0" noktasının solunda bir denklem, sağında ise başka bir denklem bulunmaktadır. Anlaşılmasını kolaylaştırmak için aşağıdakileri yapabiliriz:

Denklemler 17

Şimdi nihai denklemleri görebiliriz:

Denklemler 18

Bunu aşağıdaki şekilde de gösterebiliriz:

Denklemler 19

Açıkça söylemek gerekirse, bu fonksiyon ayrık ve yardımcı bir fonksiyon olarak kullanılmalıdır. Ancak yine de, kesirli "i" cinsinden değerleri hesaplamamıza izin verir. Elbette bunun, problemimiz bağlamında bizim için herhangi bir faydası olması pek olası değildir.

Böyle bir matematik sunduğum için, algoritma uygulamasının örneklerini de sunmak zorundayım. Bence herkes kendi sistemlerine daha kolay adapte edilebilecek hazır kod almakla ilgilenecektir. Gerekli değerlerin hesaplanmasını basitleştirecek ana değişkenleri ve metotları tanımlayarak başlayalım:

//+------------------------------------------------------------------+
//| Number of lines in the balance model                             |
//+------------------------------------------------------------------+
#define Lines 11 

//+------------------------------------------------------------------+
//| Initializing variables                                           |
//+------------------------------------------------------------------+
double MaxPercent = 10.0;
double BalanceMidK[,Lines];
double Deviations[Lines];
int Segments;
double K;

//+------------------------------------------------------------------+
//| Method for initializing required variables and arrays            |
//| Parameters: number of segments and initial balance               |
//+------------------------------------------------------------------+
void InitLines(int SegmentsInput, double BalanceInput) 
{
  Segments = SegmentsInput;
  K = BalanceInput / Segments;
  ArrayResize(BalanceMidK,Segments+1);
  ZeroStartBalances();
  ZeroDeviations();
  BuildBalances();
}

//+------------------------------------------------------------------+
//| Resetting variables for incrementing balances                    |
//+------------------------------------------------------------------+
void ZeroStartBalances()
{
  for (int i = 0; i < Lines; i++ ) 
  {
      for (int j = 0; j <= Segments; j++)
      {
          BalanceMidK[j,i] = 0.0;
      }
  }
}

//+------------------------------------------------------------------+
//| Reset deviations                                                 |
//+------------------------------------------------------------------+
void ZeroDeviations()
{
  for (int i = 0; i < Lines; i++)
  {
      Deviations[i] = -1.0;
  }
}

Kod yeniden kullanılabilir olacak şekilde tasarlanmıştır. Bir sonraki hesaplamadan sonra, önce "InitLines" metodunu çağırarak farklı bir bakiye eğrisi için göstergeyi hesaplayabiliriz. Geriye dönük testin nihai bakiyesini ve işlem sayısını belirtmemiz gerekir, ardından bu verilere dayanarak eğrilerimizi oluşturmaya başlayabiliriz:

//+------------------------------------------------------------------+
//| Constructing all balances                                        |
//+------------------------------------------------------------------+
void BuildBalances()
{
   int N0 = MathFloor(Segments / 2.0) - Segments / 2.0 == 0 ? Segments / 2 : (int)MathFloor(Segments / 2.0);//calculate first required N0
   for (int i = 0; i < Lines; i++)
   {
       if (i==0)//very first and straight line 
       {
           for (int j = 0; j <= Segments; j++)
           {
               BalanceMidK[j,i] = K*j;
           }
       }
       else//build curved lines
       {
           double ThisP = i * (MaxPercent / 10.0);//calculate current line curvature percentage
           double KDelta = ( (ThisP /100.0) * K * Segments) / (MathPow(N0,2)/2.0 );//calculation first auxiliary ratio
           double Psi0 = -KDelta * N0;//calculation second auxiliary ratio
           double KDelta1 = ((ThisP / 100.0) * K * Segments) / (MathPow(Segments-N0, 2) / 2.0);//calculate last auxiliary ratio
           //this completes the calculation of auxiliary ratios for a specific line, it is time to construct it

           for (int j = 0; j <= N0; j++)//construct the first half of the curve 
           {
               BalanceMidK[j,i] = (K + Psi0 + (KDelta * j) / 2.0) * j;
           }
           for (int j = N0; j <= Segments; j++)//construct the second half of the curve 
           {
               BalanceMidK[j,i] = BalanceMidK[i, N0] + (K + (KDelta1 * (j-N0)) / 2.0) * (j-N0);
           }
       }
   }
}

Lütfen "Lines"ın ailemizde kaç tane eğri olacağını belirlediğini unutmayın. İçbükeylik, ilgili şekilde gösterdiğim gibi sıfırdan (düz) başlayarak "MaxPercent"e kadar kademeli olarak artar. Daha sonra her bir eğri için sapmayı hesaplayabilir ve minimum olanı seçebiliriz:

//+------------------------------------------------------------------+
//| Calculation of the minimum deviation from all lines              |
//| Parameters: initial balance passed via link                      |
//| Return: minimum deviation                                        |
//+------------------------------------------------------------------+
double CalculateMinDeviation(double &OriginalBalance[])
{
   //define maximum relative deviation for each curve 
   for (int i = 0; i < Lines; i++)
   {
       for (int j = 0; j <= Segments; j++)
       {
          double CurrentDeviation = OriginalBalance[Segments] ? MathAbs(OriginalBalance[j] - BalanceMidK[j, i]) / OriginalBalance[Segments] : -1.0;
          if (CurrentDeviation > Deviations[i])
          {
              Deviations[i] = CurrentDeviation;
          }           
       }
   }
    
   //determine curve with minimum deviation and deviation itself 
   double MinDeviation=0.0;
   for (int i = 0; i < Lines; i++)
   {
       if ( Deviations[i] != -1.0 && MinDeviation == 0.0)
       {
           MinDeviation = Deviations[i];
       }
       else if (Deviations[i] != -1.0 && Deviations[i] < MinDeviation)
       {
           MinDeviation = Deviations[i];
       }
   }
   return MinDeviation;
}

Şu şekilde kullanmalıyız:

1. "OriginalBalance" orijinal bakiye dizisini tanımlarız.
2. Uzunluğunu "SegmentsInput" ve nihai bakiyesini "BalanceInput" belirleriz ve "InitLines" metodunu çağırırız.
3. Ardından "BuildBalances" metodunu çağırarak eğrileri oluştururuz.
4. Eğriler çizildiğinden, eğri ailesi için iyileştirilmiş "CalculateMinDeviation" kriterimizi dikkate alabiliriz.

Bu, kriterin hesaplanmasını tamamlar. "Curve Family Factor"ın hesaplanmasının herhangi bir zorluğa yol açmayacağını düşünüyorum. Bunu burada sunmaya gerek yok.

Alım-satım konfigürasyonları için otomatik arama 

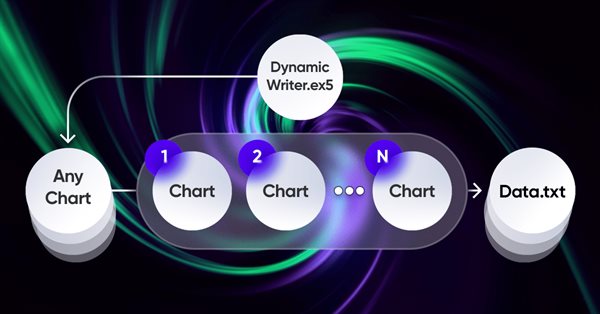
Tüm fikirdeki en önemli unsur, terminal ile programım arasındaki etkileşim sistemidir. Aslında, gelişmiş optimizasyon kriterlerine sahip döngüsel bir optimizasyon aracıdır. Bunlardan en önemlileri bir önceki bölümde ele alındı. Tüm sistemin çalışması için öncelikle MetaTrader 5 terminallerinden biri olan bir fiyat kaynağına ihtiyacımız var. Önceki makalede gösterdiğim gibi, fiyatlar benim için uygun bir formatta bir dosyaya yazılır. Bu, ilk bakışta oldukça garip bir şekilde işleyen bir Uzman Danışman kullanılarak yapılır:

Uzman Danışmanın işleyişi için benzersiz şemamı kullanmayı oldukça ilginç ve faydalı bir deneyim olarak gördüm. Burada sadece çözmem gereken problemlerin bir gösterimi var, ancak tüm bunlar alım-satım Uzman Danışmanları için de kullanılabilir:

 

Bu şemanın özelliği, istediğimiz herhangi bir grafiği seçebilmemizdir. Verilerin tekrarlanmasını önlemek için bir alım-satım aracı olarak kullanılmayacak, ancak yalnızca bir tik işleyici veya zamanlayıcı olarak işlev görecektir. Grafiklerin geri kalanı, fiyatlarını oluşturmamız gereken enstrümanları ve zaman dilimlerini temsil eder.

Fiyatların yazılması, rastgele bir sayı oluşturucusu kullanılarak rastgele bir fiyat seçimi şeklinde yapılır. Gerekirse bu süreci optimize edebiliriz. Bu temel işlev kullanılarak belirli bir süre sonra yazma işlemi gerçekleşir:

//+------------------------------------------------------------------+
//| Function to write data if present                                |
//| Write quotes to file                                             |
//+------------------------------------------------------------------+
void WriteDataIfPresent()
{
    // Declare array to store quotes 
    MqlRates rates[];
    ArraySetAsSeries(rates, false);

    // Select a random chart from those we added to the workspace 
    ChartData Chart = SelectAnyChart();
    
    // If the file name string is not empty 
    if (Chart.FileNameString != "")
    {
        // Copy quotes and calculate the real number of bars
        int copied = CopyRates(Chart.SymbolX, Chart.PeriodX, 1,
                        int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX))),
                        rates);
        
        // Calculate ideal number of bars
        int ideal = int((YearsE*(365.0*(5.0/7.0)*24*60*60)) / double(PeriodSeconds(Chart.PeriodX)));
        
        // Calculate percentage of received data 
        double Percent = 100.0 * copied / ideal;
        
        // If the received data is not very different from the desired data, 
        // then we accept them and write them to a file
        if (Percent >= 95.0)
        {
            // Open file (create it if it does not exist, 
            // otherwise, erase all the data it contained)
            OpenAndWriteStart(rates, Chart, CommonE); 
            WriteAllBars(rates); // Write all data to file
            WriteEnd(rates); // Add to end
            CloseFile(); // Close and save data file
        }
        else 
        {
            // If there are much fewer quotes than required for calculation 
            Print("Not enough data"); 
        }
    }
}

"WriteDataIfPresent" fonksiyonu, kopyalanan veriler belirtilen parametrelere göre hesaplanan ideal çubuk sayısının en az %95'i ise, seçilen grafikten fiyatlarla ilgili bilgileri bir dosyaya yazar. Kopyalanan veriler %95'ten azsa, fonksiyon "Not enough data" mesajını görüntüler. Verilen adda bir dosya mevcut değilse, fonksiyon onu oluşturur.

Bu kodun çalışması için aşağıdakilerin ek olarak tanımlanması gerekir:

//+------------------------------------------------------------------+
//| ChartData structure                                              |
//| Objective: Storing the necessary chart data                      |
//+------------------------------------------------------------------+
struct ChartData {
    string FileNameString;
    string SymbolX;
    ENUM_TIMEFRAMES PeriodX;
};

//+------------------------------------------------------------------+
//| Randomindex function                                             |
//| Objective: Get a random number with uniform distribution         |
//+------------------------------------------------------------------+
int Randomindex(int start, int end) {
    return start + int((double(MathRand())/32767.0)*double(end-start+1));
}

//+------------------------------------------------------------------+
//| SelectAnyChart function                                          |
//| Objective: View all charts except current one and select one of  |
//|       them to write quotes                                       |
//+------------------------------------------------------------------+
ChartData SelectAnyChart() {
    ChartData chosenChart;
    chosenChart.FileNameString = "";
    int chartCount = 0;
    long currentChartId, previousChartId = ChartFirst();

    // Calculate number of charts
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;  
        }
        previousChartId = currentChartId;
        
        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }

    int randomChartIndex = Randomindex(0, chartCount - 1);
    chartCount = 0;
    currentChartId = ChartFirst(); 
    previousChartId = currentChartId;
    
    // Select random chart
    while (currentChartId = ChartNext(previousChartId)) {
        if(currentChartId < 0) {
            break;
        }
        
        previousChartId = currentChartId;
        
        // Fill in selected chart data
        if (chartCount == randomChartIndex) {
            chosenChart.SymbolX = ChartSymbol(currentChartId);
            chosenChart.PeriodX = ChartPeriod(currentChartId);
            chosenChart.FileNameString = "DataHistory" + " " + chosenChart.SymbolX + " " + IntegerToString(CorrectPeriod(chosenChart.PeriodX));
        }
        
        if (chartCount > randomChartIndex) {
            break;
        }

        if (currentChartId != ChartID()) {
            chartCount++;
        }
    }
       
    return chosenChart;
}

Bu kod, şu anda terminalde açılabilen çeşitli grafiklerden farklı dövizler için geçmiş finansal piyasa verilerini (fiyatlar) kaydetmek ve analiz etmek için kullanılır.

• "ChartData" yapısı, dosya adı, sembol (döviz çifti) ve zaman dilimi dahil olmak üzere her grafikle ilgili verileri depolamak için kullanılır. 
• "Randomindex(start, end)" fonksiyonu "start" ve "end" arasında rastgele bir sayı üretir. Bu, mevcut grafiklerden birini rastgele seçmek için kullanılır.
• "SelectAnyChart()", geçerli grafik hariç tüm açık ve kullanılabilir grafiklerden üzerinden geçer ve ardından işlenmek üzere bunlardan birini rastgele seçer.

Oluşturulan fiyatlar program tarafından otomatik olarak alınır ve ardından karlı konfigürasyonlar otomatik olarak aranır. Tüm süreci otomatikleştirmek oldukça karmaşıktır, ancak bunu tek bir şekle sığdırmaya çalıştım:

Şekil 5

Bu algoritmanın üç durumu vardır:

1. Devre dışı.
2. Fiyatlar bekleniyor.
3. Aktif.

Fiyatları kaydetmek için kullanılan Uzman Danışman henüz bir dosya oluşturmadıysa veya belirtilen klasördeki tüm fiyatları sildiysek, algoritma sadece bunların görünmesini bekler ve bir süre duraklar. Sizin için MQL5 tarzında uyguladığım iyileştirilmiş kriterimize gelince, hem brute force hem de optimizasyon için de uygulanmaktadır:

Şekil 6

Gelişmiş mod eğri ailesi faktörünü çalıştırırken, standart algoritma sadece doğrusallık faktörünü kullanır. Geri kalan iyileştirmeler bu makaleye sığmayacak kadar kapsamlıdır. Bir sonraki makalede, evrensel çok dövizli şablona dayalı olarak Uzman Danışmanları bir araya getirmek için yeni algoritmamı göstereceğim. Şablon tek bir grafikte başlatılır, ancak her Uzman Danışmanın kendi grafiğinde başlatılmasına gerek kalmadan tüm birleştirilmiş alım-satım sistemlerini yönetir. İşlevselliğinin bir kısmı bu makalede kullanılmıştır.

Sonuç

Bu makalede, alım-satım sistemlerini geliştirme ve optimize etme sürecini otomatikleştirme alanındaki yeni olanakları ve fikirleri daha ayrıntılı olarak inceledik. Ana başarılar, yeni bir optimizasyon algoritmasının geliştirilmesi, bir terminal senkronizasyon mekanizmasının ve otomatik bir optimizasyon aracının ve önemli bir optimizasyon kriteri olan eğri faktörü ve eğri ailesinin oluşturulmasıdır. Bu, geliştirme süresini azaltmamızı ve elde edilen sonuçların kalitesini artırmamızı sağlar.

Önemli bir ekleme de, ters ileri dönemler bağlamında daha gerçekçi bir bakiye modelini temsil eden içbükey eğriler ailesidir. Her eğri için uyum faktörünü hesaplamak, otomatik alım-satım için en uygun ayarları daha doğru bir şekilde seçmemizi sağlar.

Linkler

• Model aramada brute force yaklaşımı (Bölüm V): Farklı bir bakış açısı
  
• Model aramada brute force yaklaşımı (Bölüm IV): Asgari işlevsellik
• Model aramada brute force yaklaşımı (Bölüm III): Yeni ufuklar
  
• Model aramada brute force yaklaşımı (Bölüm II): Yoğunlaşma
  
• Model aramada brute force yaklaşımı