
Нейросети - это просто
Содержание
- Введение
- 1. Принципы построения искусственных нейронных сетей
- 2. Как устроен искусственный нейрон
- 3. Обучение сети
- 4. Строим свою нейронную сеть средствами MQL
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Все большие аспекты нашей жизнедеятельности охватывает искусственный интеллект. Все чаще новостные ленты пестрят сообщениями "нейросеть научили ..." И каждый раз, когда речь заходит об искусственном интеллекте, мы рисуем в своей голове какие-то фантастические образы. Кажется, что это что-то сложное, сверхъестественное и необъяснимое. И создание такого чуда под силу только большой группе ученных мужей. И конечно, мы можем только восхищаться, при этом никогда не сможем повторить нечто даже приближенное на своем домашнем ПК. Но поверьте: "не так страшен черт, как его малюют". Давайте попробуем разобраться, что же представляют из себя нейронные сети, и как можно их применить в нашей торговле.
1. Принципы построения искусственных нейронных сетей
В Википедии дано такое определение нейросети:
"Иску́сственная нейро́нная се́ть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма."
Т.е. искусственная нейронная сеть — это некая сущность, состоящая из массива искусственных нейронов с организованной взаимосвязью между ними. При этом организация взаимосвязей между нейронами создана по образу и подобию процессов в мозгу живого организма.
На рисунке ниже представлена схема простой нейронной сети. На ней кружочками обозначены нейроны, а линиями показаны связи между нейронами. Как видно на рисунке, нейроны расположены слоями, которые делят на 3 группы. Синим цветом обозначен слой входных нейронов на которые подается исходная информация. Зеленым и красным обозначены выходные нейроны, которые выдают результат работы нейронной сети. Между ними расположены серые нейроны, образующие, так называемый скрытый слой.
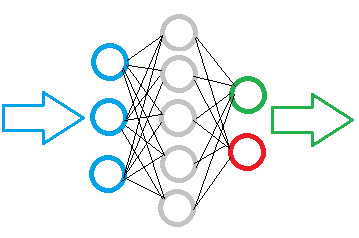
Несмотря на различие слоев, вся нейронная сеть построена из одинаковых нейронов, имеющих несколько элементов для входных сигналов и только один для выдачи результата. Внутри нейрона организована обработка поступившей информации с выдачей простого логического результата. К примеру, "Да" или "Нет". Применительно к теме торговли это может быть сигнал на сделку или указывать ее направление.
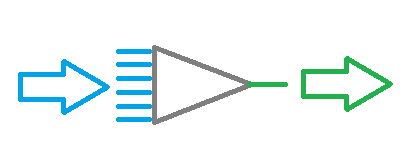
Исходная информация попадает на слой входных нейронов, обрабатывается и результат работы нейронов служит исходной информацией для нейронов последующего слоя. Операции повторяются от одного слоя к другому, пока не будет достигнут слой выходных нейронов. Таким образом, исходная информация обрабатывается и фильтруется от слоя к слою и на выходе нейронная сеть выдает некий результат.
В зависимости от сложности решаемых задач и создаваемых моделей количество нейронов в каждом слое может варьироваться. А также возможны вариации нейронных сетей с несколькими скрытыми слоями. Все это делает нейронную сеть более сложной, что позволяет решать более сложные задачи. Но в тоже время и требует больших вычислительных ресурсов.
Поэтому при создании своей модели нейронной сети нам нужно четко понимать какую информацию и в каком объеме мы будем обрабатывать, а также, что мы хотим получить в результате. От этого зависит количество необходимых нейронов в слоях модели.
Если мы хотим подать на вход нейронной сети некий массив данных из 10 элементов, то входной слой сети должен содержать 10 нейронов. Это позволит принять весь массив данных. Избыточные входные нейроны будут лишь балластом.
Количество выходных нейронов определяется ожидаемым результатом. Для получения однозначного логического результата достаточно одного выходного нейрона. Если требуется получить ответ на несколько вопросов, то необходимо создать по одному нейрону на каждый вопрос.
Скрытые слои нейронной сети являются неким аналитическим центром, который обрабатывает и анализирует полученную информацию. Следовательно, количество нейронов в слое зависит от вариативности данных предыдущего слоя, т.е. каждый нейрон предполагает некую гипотезу развития событий.
Количество скрытых слоев определяется причинно-следственной связью между исходными данными и ожидаемым результатом. К примеру, если мы строим нашу модель применительно к технике "5 почему", то логично использовать 4 скрытых слоя, которые в сумме с выходным слоем дадут возможность поставить 5 вопросов к исходным данным.
Подытожим:
- нейронная сеть строится из одинаковых нейронов, следовательно, для построения модели нам достаточно создать один класс нейронов;
- нейроны в модели организованы слоями;
- поток информации в нейронной сети организован в виде последовательной передачи данных через все слои модели от входных нейронов к выходным;
- количество входных нейронов обусловлено объемом анализируемой информации за один проход, а количество выходных нейронов — объемом результирующих данных;
- т.к. на выходе нейрона формируется некий логический результат, то и вопросы поставленные перед нейронной сетью должны предполагать однозначный ответ.
2. Как устроен искусственный нейрон
Получив представление о структуре нейронной сети, давайте рассмотрим построение модели искусственного нейрона. Ведь именно в его недрах осуществляются математические вычисления и принимается решения. И тут возникает вопрос: каким образом реализовать множество различных решений из одних исходных данных используя одну математическую формулу. Решение было найдено в изменении связей между нейронами. Для каждой связи определяется некий весовой коэффициент, который определяет влияние данного входного значения на результат принимаемого решения.
Математическая модель нейрона состоит из двух функций. Вначале суммируются произведения входных данных на их весовые коэффициенты.
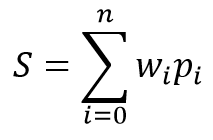
А затем на основании полученного значения вычисляется результирующее значение в, так называемой, функции активации. На практике применяются различные варианты функции активации, но наибольшее распространение получили такие функции:
- Сигмовидная функция — диапазон возвращаемых значений от "0" до "1"
- Гиперболический тангенс — диапазон возвращаемых значений от "-1" до "1"
Выбор функции активации зависит от решаемых задач. Так, если в результате обработки исходных данных ожидаем получить логический ответ, то предпочтение отдается сигмовидной функции. В реалиях трейдинга, я предпочитаю использовать гиперболический тангенс. Где значение "-1" соответствует сигналу на продажу, а значение "1" — сигналу на покупку. Результат между пороговыми значениями говорит о некой неопределенности.
3. Обучение сети
Как выше было сказано, вариативность результатов каждого нейрона и нейронной сети в целом зависит от подобранных весовых коэффициентов для связей между нейронами. Решение задачи подбора правильных весовых коэффициентов называется обучением нейронной сети.
Для обучения нейронной сети существуют различные алгоритмы и методы:
- Обучение с учителем;
- Обучение без учителя;
- Обучение с подкреплением.
Метод обучения определяется от наличия исходных данных и поставленных перед нейронной сетью задач.
Обучение с учителем используется при наличии достаточного набора исходных данных с соответствующими правильными ответами на поставленные вопросы. В процессе обучения на вход нейронной сети подаются исходные данные и полученный на выходе сети результат сверяется с заведомо известным правильным ответом. После чего корректируются веса в сторону снижения ошибки.
Обучение без учителя применяется при наличии массива исходных данных и отсутствии правильных ответов на поставленные вопросы. При таком обучении нейронная сеть ищет схожие наборы данных и позволяет разделить исходные данные на схожие группы.
Обучение с подкреплением применяется когда нет правильных ответов, но есть понимание того, что должны получить в итоге. В ходе обучения на вход нейросети подаются исходные данные и сеть пытается решить задачу. После проверки результата дается обратная связь сети в виде определенной награды. В процессе обучения нейронная сеть стремиться к максимальной награде.
В данной статье мы будем использовать обучение с учителем. В качестве примера я выбрал метод обратного распространения ошибки. Такой подход позволяет организовать постоянное обучение нейронной сети в режиме реального времени.
В основе данного метода лежит использование выходной ошибки нейронной сети для коррекции ее весов. Сам алгоритм обучения состоит из двух этапов. Вначале на основании входных данных рассчитывается результирующее значение нейронной сети, которое сравнивается с эталонным и вычисляется ошибка. Далее осуществляется обратный проход с распространением ошибки от выхода сети к ее входам с коррекцией всех весовых коэффициентов. Данный подход итеративный и обучение сети осуществляется пошагово, что позволяет после обучения на исторических данных перейти к обучению сети в режиме online.
Метод обратного распространения ошибки использует стохастический градиентный спуск, что позволяет достичь приемлемого минимума ошибки. А благодаря возможности обучения нейронной сети online, поддерживать этот минимум на длительном временном интервале.
4. Строим свою нейронную сеть средствами MQL
После осмысления теории работы нейронных сетей можно перейти к практической части статьи. Чтобы лучше показать алгоритм работы НС, я предлагаю сделать пример полностью средствами языка MQL5 без использования сторонних библиотек. И начнем мы работу с создания классов для хранения данных об элементарных связях между нейронами.
4.1. Связи
Вначале создадим класс СConnection для хранения весового коэффициента одной связи. И создадим его наследником класса CObject. Данный класс будет содержать две переменные типа double: weight для хранения непосредственно значения весового коэффициента и deltaWeight, в которой будем хранить величину последнего изменения весового коэффициента (используется при обучении). Чтобы не использовать дополнительные методы для работы с переменными сделаем их публичными. Начальное значение переменных будет задаваться в конструкторе класса.
class СConnection : public CObject { public: double weight; double deltaWeight; СConnection(double w) { weight=w; deltaWeight=0; } ~СConnection(){}; //--- methods for working with files virtual bool Save(const int file_handle); virtual bool Load(const int file_handle); };
Также, для возможности последующего сохранения информации о связях создадим методы сохранения данных в файл Save и последующего чтения Load. Данные методы построены по классической схеме с получением хендла файла в параметрах метода, проверяем его состоятельность и записываем данные (или считываем в методе Load).
bool СConnection::Save(const int file_handle) { if(file_handle==INVALID_HANDLE) return false; //--- if(FileWriteDouble(file_handle,weight)<=0) return false; if(FileWriteDouble(file_handle,deltaWeight)<=0) return false; //--- return true; }
Следующим шагом создадим массив для хранения весов CArrayCon на базе класса CArrayObj. Здесь мы переопределим два виртуальных метода CreateElement и Type. Первый будет использоваться для создания нового элемента, а второй будет идентифицировать наш класс.
class CArrayCon : public CArrayObj { public: CArrayCon(void){}; ~CArrayCon(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7781); } };
В параметрах метода создания нового элемента CreateElement будем передавать индекс создаваемого элемента. В самом методе проверим его действительность, проверим размер массива хранения данных и изменим его при необходимости. А затем создадим новый экземпляр класса СConnection, задав начальный вес случайной величиной.
bool CArrayCon::CreateElement(const int index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- m_data[index]=new СConnection(MathRand()/32767.0); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; m_data_total=MathMax(m_data_total,index); //--- return (true); }
4.2. Нейрон
Следующим шагом создадим искусственный нейрон. Как я уже писал выше, в качестве функции активации для своего нейрона я использую гиперболический тангенс. Диапазон результирующих значений данной функции лежит от "-1" до "1". Значение "-1" дает сигнал на продажу, а "1" — на покупку.
Класс искусственного нейрона CNeuron, также как и предыдущий элемент СConnection, создадим наследником класса CObject, но его структура будет немного сложнее.
class CNeuron : public CObject { public: CNeuron(uint numOutputs,uint myIndex); ~CNeuron() {}; void setOutputVal(double val) { outputVal=val; } double getOutputVal() const { return outputVal; } void feedForward(const CArrayObj *&prevLayer); void calcOutputGradients(double targetVals); void calcHiddenGradients(const CArrayObj *&nextLayer); void updateInputWeights(CArrayObj *&prevLayer); //--- methods for working with files virtual bool Save(const int file_handle) { return(outputWeights.Save(file_handle)); } virtual bool Load(const int file_handle) { return(outputWeights.Load(file_handle)); } private: double eta; double alpha; static double activationFunction(double x); static double activationFunctionDerivative(double x); double sumDOW(const CArrayObj *&nextLayer) const; double outputVal; CArrayCon outputWeights; uint m_myIndex; double gradient; };
В параметрах конструктора класса передадим количество исходящих связей нейрона и его порядковый номер в слое (потребуется для последующей идентификации нейрона). В теле метода зададим константы, сохраним полученные данные и создадим массив исходящих связей.
CNeuron::CNeuron(uint numOutputs, uint myIndex) : eta(0.15), // net learning rate alpha(0.5) // momentum { for(uint c=0; c<numOutputs; c++) { outputWeights.CreateElement(c); } m_myIndex=myIndex; }
Методы setOutputVal и getOutputVal служат для обращения к результирующему значению нейрона. Непосредственный расчет результирующего значения нейрона осуществляется в методе feedForward. В параметрах данный метод получает предшествующий слой нейронов.
void CNeuron::feedForward(const CArrayObj *&prevLayer) { double sum=0.0; int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *temp=prevLayer.At(n); double val=temp.getOutputVal(); if(val!=0) { СConnection *con=temp.outputWeights.At(m_myIndex); sum+=val * con.weight; } } outputVal=activationFunction(sum); }
В теле метода организован цикл по перебору всех нейронов предыдущего слоя и суммирования произведения результирующих значений нейронов с весовыми коэффициентами. После расчета суммы вычисляется результирующее значение нейрона в методе activationFunction (функция активации нейрона вынесена в отдельный метод).
double CNeuron::activationFunction(double x) { //output range [-1.0..1.0] return tanh(x); }
Следующий блок методов используется при обучении нейронной сети. Вначале создадим метод вычисления производной для функции активации activationFunctionDerivative. Это необходимо чтобы определить какое требуется изменение суммирующей функции для компенсации ошибки результирующего значения нейрона.
double CNeuron::activationFunctionDerivative(double x) { return 1/MathPow(cosh(x),2); }
Далее создаем два метода расчета градиента для корректировки весовых коэффициентов. Необходимость создания 2-х методов обусловлена различием в расчете ошибки результирующего значения для нейронов выходного слоя и скрытых слоев. Для выходного слоя ошибка рассчитывается как разница результирующего и эталонного значения, в то время как для нейронов скрытых слоев ошибка рассчитывается как сумма градиентов всех нейронов последующего слоя взвешенных на весовые коэффициенты связей между нейронами. Данный расчет вынесен в отдельный метод sumDOW.
void CNeuron::calcHiddenGradients(const CArrayObj *&nextLayer) { double dow=sumDOW(nextLayer); gradient=dow*CNeuron::activationFunctionDerivative(outputVal); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CNeuron::calcOutputGradients(double targetVals) { double delta=targetVals-outputVal; gradient=delta*CNeuron::activationFunctionDerivative(outputVal); }
Затем градиент определяется как произведение ошибки на производную от функции активации.
Рассмотрим детальнее метод определения ошибки нейрона скрытого слоя sumDOW. В параметрах данные метод получает указатель на последующий слой нейронов. В теле метода сначала обнуляем итоговую переменную sum, затем организуем цикл по перебору всех нейронов последующего слоя и просуммируем произведение градиентов нейронов на весовой коэффициент связи с ним.
double CNeuron::sumDOW(const CArrayObj *&nextLayer) const { double sum=0.0; int total=nextLayer.Total()-1; for(int n=0; n<total; n++) { СConnection *con=outputWeights.At(n); CNeuron *neuron=nextLayer.At(n); sum+=con.weight*neuron.gradient; } return sum; }
После проведенной выше подготовительной работы осталось создать метод пересчета весовых коэффициентов updateInputWeights. В моей модели нейрон хранит исходящие весовые коэффициенты, поэтому метод обновления весовых коэффициентов получает в параметрах предшествующий слой нейронов.
void CNeuron::updateInputWeights(CArrayObj *&prevLayer) { int total=prevLayer.Total(); for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron= prevLayer.At(n); СConnection *con=neuron.outputWeights.At(m_myIndex); con.weight+=con.deltaWeight=eta*neuron.getOutputVal()*gradient + alpha*con.deltaWeight; } }
В теле метода создан цикл по перебору всех нейронов предыдущего слоя с корректировкой их весовых коэффициентов влияния именно на текущий нейрон.
Хочу обратить внимание, что корректировка весов осуществляется с применением двух коэффициентов eta (притупляет реакцию на текущее отклонение) и alpha (коэффициент инертности). Подобный подход помогает в некоторой мере усреднить влияние ряда последующих итераций обучения и отсеять шумовые данные.
4.3. Нейронная сеть
После создания искусственного нейрона нам предстоит объединить созданные объекты в единую сущность — нейронную сеть. Мы должны понимать, что создаваемые объекты должны быть гибкими и позволять создавать нейронные сети различных конфигураций. Это позволит нам воспользоваться плодами наших трудов для решения различных задач.
Как уже писалось выше, нейронная сеть состоит из слоев нейронов. Следовательно, первое, что мы сделаем, это объединим нейроны в слой. Для этого создадим класс CLayer, унаследовав основные методы от класса CArrayObj.
class CLayer: public CArrayObj { private: uint iOutputs; public: CLayer(const int outputs=0) { iOutputs=outpus; }; ~CLayer(void){}; //--- virtual bool CreateElement(const int index); virtual int Type(void) const { return(0x7779); } };
В параметрах метода инициализации класса CLayer зададим количество элементов последующего слоя. А также мы перепишем два виртуальных метода CreateElement (создание нового нейрона слоя) и Type (метод идентификации объекта).
При создании нового нейрона укажем его порядковый номер в параметрах метода. В теле метода сначала проверим действительность полученного индекса. Затем проверим размер массива для хранения указателей на экземпляры объектов нейрона, при необходимости увеличим размер массива. Далее создадим новый нейрон. При успешном создании нового экземпляра нейрона, зададим его начальное значение и изменим количество объектов в массиве и выходим из метода с результатом true.
bool CLayer::CreateElement(const uint index) { if(index<0) return false; //--- if(m_data_max<index+1) { if(ArrayResize(m_data,index+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CNeuron *neuron=new CNeuron(iOutputs,index); if(!CheckPointer(neuron)!=POINTER_INVALID) return false; neuron.setOutputVal((neuronNum%3)-1) //--- m_data[index]=neuron; m_data_total=MathMax(m_data_total,index); //--- return (true); }
Аналогичным подходом создадим класс CArrayLayer для хранения указателей на слои нашей сети.
class CArrayLayer : public CArrayObj { public: CArrayLayer(void){}; ~CArrayLayer(void){}; //--- virtual bool CreateElement(const uint neurons, const uint outputs); virtual int Type(void) const { return(0x7780); } };
Отличие от предыдущего класса можно увидеть в специфике метода создания нового элемента массива CreateElement. В параметры этого метода передадим количество нейронов в создаваемом и последующем слоях. В теле метода поверим количество нейронов в создаваемом слое. При отсутствии нейронов в создаваемом слое, выходим из метода с значением false. Далее проверяем необходимость изменения размера массива для хранения указателей. И затем переходим непосредственно к созданию экземпляров объектов: создаем новый слой и организовываем цикл по созданию нейронов. На каждом шаге проверяем созданный объект. При появлении ошибки выходим из метода с значением false. После создания всех элементов сохраняем в массиве указатель на созданный слой и выходим из метода с результатом true.
bool CArrayLayer::CreateElement(const uint neurons, const uint outputs) { if(neurons<=0) return false; //--- if(m_data_max<=m_data_total) { if(ArrayResize(m_data,m_data_total+10)<=0) return false; m_data_max=ArraySize(m_data)-1; } //--- CLayer *layer=new CLayer(outputs); if(!CheckPointer(layer)!=POINTER_INVALID) return false; for(uint i=0; i<neurons; i++) if(!layer.CreatElement(i)) return false; //--- m_data[m_data_total]=layer; m_data_total++; //--- return (true); }
Создание отдельных классов для слоя и массива слоев позволяет нам создавать нейронные сети различной конфигурации без изменения самих классов. Мы получили довольно гибкую сущность, позволяющая извне задавать количество слоев и нейронов в каждом слое.
И наконец переходим к созданию класса нашей нейронной сети CNet.
class CNet { public: CNet(const CArrayInt *topology); ~CNet(){}; void feedForward(const CArrayDouble *inputVals); void backProp(const CArrayDouble *targetVals); void getResults(CArrayDouble *&resultVals); double getRecentAverageError() const { return recentAverageError; } bool Save(const string file_name, double error, double undefine, double forecast, datetime time, bool common=true); bool Load(const string file_name, double &error, double &undefine, double &forecast, datetime &time, bool common=true); //--- static double recentAverageSmoothingFactor; private: CArrayLayer layers; double recentAverageError; };
Благодаря проделанной выше работе сам класс нейронной сети содержит минимум переменных и методов. В представленном коде только две статические переменные для расчета и хранения средней ошибки (recentAverageSmoothingFactor и recentAverageError) и указатель на массив слоев нашей нейронной сети layers.
Давайте подробнее остановимся на методах данного класса. В параметрах конструктора класса передается указатель на массив данных типа int. Количество элементов в массиве указывает на количество слоев в создаваемой нейронной сети, а каждый элемент массива содержит количество нейронов в соответствующем слое. Таким образом, мы делаем наш класс универсальным для создания практически любой сложности нейронной сети.
CNet::CNet(const CArrayInt *topology) { if(CheckPointer(topology)==POINTER_INVALID) return; //--- int numLayers=topology.Total(); for(int layerNum=0; layerNum<numLayers; layerNum++) { uint numOutputs=(layerNum==numLayers-1 ? 0 : topology.At(layerNum+1)); if(!layers.CreateElement(topology.At(layerNum), numOutputs)) return; } }
В теле метода проверяем действительность переданного указателя и организовываем цикл по созданию слоев нейронной сети. Надо сказать, что для выходного слоя нейронов указывается нулевое количество выходных связей.
Метод feedForward предназначен для расчета значения нейронной сети. В параметрах метод получает массив входных значений, на основании которых будут рассчитываться результирующие значения нейронной сети.
void CNet::feedForward(const CArrayDouble *inputVals) { if(CheckPointer(inputVals)==POINTER_INVALID) return; //--- CLayer *Layer=layers.At(0); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=inputVals.Total(); if(total!=Layer.Total()-1) return; //--- for(int i=0; i<total && !IsStopped(); i++) { CNeuron *neuron=Layer.At(i); neuron.setOutputVal(inputVals.At(i)); } //--- total=layers.Total(); for(int layerNum=1; layerNum<total && !IsStopped(); layerNum++) { CArrayObj *prevLayer = layers.At(layerNum - 1); CArrayObj *currLayer = layers.At(layerNum); int t=currLayer.Total()-1; for(int n=0; n<t && !IsStopped(); n++) { CNeuron *neuron=currLayer.At(n); neuron.feedForward(prevLayer); } } }
В теле метода проверим действительность полученного указателя и нулевого слоя нашей сети. Затем полученные исходные данные зададим в качестве результирующих значений нейронов нулевого слоя и организуем двойной цикл с поэтапным пересчетом результирующих значений нейронов по всей нейронной сети от первого скрытого слоя до выходных нейронов.
Для получения самого результата предназначен метод getResults, в котором организован цикл по сбору результирующих значений с нейронов выходного слоя.
void CNet::getResults(CArrayDouble *&resultVals) { if(CheckPointer(resultVals)==POINTER_INVALID) { resultVals=new CArrayDouble(); } resultVals.Clear(); CArrayObj *Layer=layers.At(layers.Total()-1); if(CheckPointer(Layer)==POINTER_INVALID) { return; } int total=Layer.Total()-1; for(int n=0; n<total; n++) { CNeuron *neuron=Layer.At(n); resultVals.Add(neuron.getOutputVal()); } }
Процесс обучения нейронной сети построен в методе backProp. В параметрах метод получает массив эталонных значений. В теле метода проверяем действительность полученного массива и считаем среднеквадратичную ошибку результирующего слоя. Затем в цикле пересчитываем градиенты нейронов во всех слоях. После чего в последнем цикле метода актуализируем весовые коэффициенты связей между нейронами на основании рассчитанных ранее градиентов.
void CNet::backProp(const CArrayDouble *targetVals) { if(CheckPointer(targetVals)==POINTER_INVALID) return; CArrayObj *outputLayer=layers.At(layers.Total()-1); if(CheckPointer(outputLayer)==POINTER_INVALID) return; //--- double error=0.0; int total=outputLayer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); double delta=targetVals[n]-neuron.getOutputVal(); error+=delta*delta; } error/= total; error = sqrt(error); recentAverageError+=(error-recentAverageError)/recentAverageSmoothingFactor; //--- for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=outputLayer.At(n); neuron.calcOutputGradients(targetVals.At(n)); } //--- for(int layerNum=layers.Total()-2; layerNum>0; layerNum--) { CArrayObj *hiddenLayer=layers.At(layerNum); CArrayObj *nextLayer=layers.At(layerNum+1); total=hiddenLayer.Total(); for(int n=0; n<total && !IsStopped();++n) { CNeuron *neuron=hiddenLayer.At(n); neuron.calcHiddenGradients(nextLayer); } } //--- for(int layerNum=layers.Total()-1; layerNum>0; layerNum--) { CArrayObj *layer=layers.At(layerNum); CArrayObj *prevLayer=layers.At(layerNum-1); total=layer.Total()-1; for(int n=0; n<total && !IsStopped(); n++) { CNeuron *neuron=layer.At(n); neuron.updateInputWeights(prevLayer); } } }
Чтобы не переобучать нашу нейронную сеть при перезапуске программы, создадим методы сохранения данных в локальный файл Save и последующей загрузки данных из файла Load.
Более подробно с кодом всех методов класса можно ознакомиться во вложении.
Заключение
В данной статье я попытался рассказать и показать как можно создать нейронную сеть для своих нужд в домашних условиях. Конечно, это лишь вершина айсберга. И в статье рассмотрен лишь один из возможных вариантов — перцептрон, предложенный Фрэнком Розенблаттом в далеком 1957 году. С тех пор прошло уже более 60 лет и появились другие модели. Но данная модель по прежнему жизнеспособна и дает неплохие результаты, в чем каждый может удостовериться на собственном опыте. Для желающих более глубоко погрузиться в тему искусственного интеллекта я посоветую обратиться к соответствующей литературе, т.к. полностью раскрыть труды ученых мужей не возможно даже в серии статей.
Ссылки
Программы, используемые в статье:
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети (перцетрона) |
 Мультивалютный мониторинг торговых сигналов (Часть 1): Разработка структуры приложения
Мультивалютный мониторинг торговых сигналов (Часть 1): Разработка структуры приложения
 Эконометрический подход к поиску рыночных закономерностей: автокорреляция, тепловые карты и диаграммы рассеяния
Эконометрический подход к поиску рыночных закономерностей: автокорреляция, тепловые карты и диаграммы рассеяния
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Техника "5 почему" построена на последовательных вопросах, когда каждый вопрос отвечает на причину предыдущего. К примеру, мы смотрим на график и растущий график цены и и строим вопросы (вопросы ответы даны абстрактно для разъяснения техники):
1. Куда торговать? - Покупать
2. Почему покупать? - Потому-что растущий тренд
3. Почему растущий тренд? - МА50 растет
4. Почему МА50 растет? - средня цена закрытия 50 свечей со сдвигом 1 ниже средней цены закрытия 50 последних свечей.
и т.д.
Т.к. вопросы последовательны и имеют причинно-следственную связь, то создаем слои для соблюдения этой связи. Если мы используем только 2 слоя, то теряется причинно- следственная связь, нейросеть анализирует ряд независимых вариантов и выбирает лучший.
Вот читаю и думаю: в этом, кажется, есть смысл.
Но смысла нет! Я делаю нейронную сеть с 1 слоем, и она выдает хороший результат. Я добавляю второй слой, и результат хуже.
Значит, количество слоев определяется не логическими рассуждениями, а результатом работы. У вас нет результата работы, вы не заморачивались на тему, является ли это стратегией, поэтому вам кажется, что это что-то с чем-то.
И еще. Почему вы думаете, что покупка и продажа - это разные решения нейронной сети? Покупка и продажа - это одно и то же решение о покупке актива. Иначе получается совсем несуразица. Вы что же собираетесь подавать отрицательные значения осциллятора на входы, чтобы получить выход меньше нуля, и положительные значения, чтобы получить выход больше нуля? Но вообще-то, если осциллятор ниже нуля, это зона перепроданности, и надо-таки покупать, а не продавать.
Короче, подумайте о результате, и дело сразу пойдет в другом направлении. Бедный, бедный Розенблат...
Вот читаю и думаю: в этом, кажется, есть смысл.
Но смысла нет! Я делаю нейронную сеть с 1 слоем, и она выдает хороший результат. Я добавляю второй слой, и результат хуже.
Значит, количество слоев определяется не логическими рассуждениями, а результатом работы. У вас нет результата работы, вы не заморачивались на тему, является ли это стратегией, поэтому вам кажется, что это что-то с чем-то.
И еще. Почему вы думаете, что покупка и продажа - это разные решения нейронной сети? Покупка и продажа - это одно и то же решение о покупке актива. Иначе получается совсем несуразица. Вы что же собираетесь подавать отрицательные значения осциллятора на входы, чтобы получить выход меньше нуля, и положительные значения, чтобы получить выход больше нуля? Но вообще-то, если осциллятор ниже нуля, это зона перепроданности, и надо-таки покупать, а не продавать.
Короче, подумайте о результате, и дело сразу пойдет в другом направлении. Бедный, бедный Розенблат...
Используя 1 нейрон Вы приходите к функции автокорреляции.
А рассуждая о покупке и продаже, да, в обоих случаях это покупка только разных активов. И нейросеть принимает решение о покупке того или иного актива на основе анализа одних и тех же данных, подаваемых на вход. А решение принимается на основании анализа обучающей выборки. В ходе обучения меняются весовые коэффициенты, при этом может измениться и его знак на противоположный.
метод 5 почему аналогичен дереву решений, также поэтапно сужается область поиска решения/причины. Всё-таки непонятно как это связано с тем, что используется 4 слоя в НС в такой структуре. Я понимаю еще структура была бы хитромудрая, например на второй слой подается просуммированный выход первого слоя и неизмененный входной сигнал и т.п.
Подскажите, вы опирались на какие-то другие работы, где использовались такие основания для выбора кол-ва слоев? Или это ваше ноу-хау?
з.ы. Работа хорошая, спасибо.
а на это можете ответить?
а на это можете ответить?
Метод 5-почему дан образно. Количество слоев, зачастую, подбирается экспериментальным путем. В литературе упоминается, что сети с одним скрытым слоям применяются для задач, в которых объекты можно поделить на 2 части линейно. Рост количества слоев позволяет решать более сложные задачи.
" if(!CheckPointer(neuron)!=POINTER_INVALID) "
по моему лишние восклицательные знаки
Наверно проще так записывать:
if(CheckPointer(neuron)==POINTER_INVALID)
return false;