Locatário

Novo comentário
 

Olá a todos!

Tenho permissão para usar um depósito de rublos X0 durante t meses. Todo mês, uma porcentagem fixa q do valor atual do depósito X é depositada. Estou autorizado a retirar mensalmente uma porcentagem k da conta, que não excede o valor de q.

Portanto, a tarefa é maximizar a quantidade de dinheiro retirado durante um período de t meses. Parece óbvio que retirar todos os juros acumulados q todo mês não é a melhor opção, pois neste caso o depósito não cresce e com menos carga na conta, a quantia eventualmente retirada pode ser maior... Por outro lado, o valor de k não deve ir a zero, pois neste caso a quantidade de dinheiro retirado também vai a zero. Aparentemente, a verdade está em algum lugar no meio. Mas onde exatamente?

Ajude-me a resolver este problema analiticamente de uma maneira geral.

P.S. não postou em um ramo de zadacha não relacionado ao comércio, porque o tópico proposto está relacionado a este último.

 
Parece que você tem que fazer igualdade de equações e depois diferenciá-las (o problema lembra uma ambulância, quando você pode pegar um atalho em um campo em baixa velocidade, ou dirigir no asfalto em uma velocidade maior, mas em uma rota mais longa - em que ponto você sai do asfalto para o campo?)
 

Então a questão é: como você os inventa? Até agora, só funciona de forma iterativa:


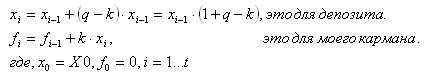
Precisamos apresentá-lo de forma analítica (como uma dependência funcional do tempo t).

 
Expanda ainda mais a fórmula para f, ou seja, leve-a para fi = fi(x0).
 

Aha! Então, acontece assim:

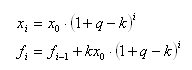
E a expressão para a quantidade de dinheiro retirado durante um período de t meses pode ser escrita como:

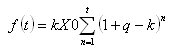
Se assim for, é melhor assim. O que segue? Você tem que se livrar da quantia...

 

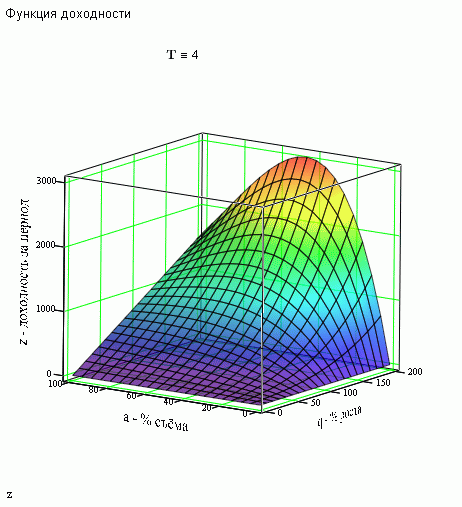
se pareceria algo assim.

 

De jeito nenhum!...

Você pode ser mais específico? Quero dizer, sob a forma de uma fórmula.

Assim você pode realmente ver o melhor em termos de porcentagem de remoção!

 
Neutron:

Se assim for, é melhor assim. O que vem a seguir? Temos que nos livrar da soma...

Lembre-se da fórmula para a soma dos primeiros n termos de uma progressão geométrica


 
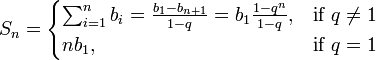
onde q é o denominador do GP, b1 é o primeiro termo
 
alsu:

lembrar a fórmula para a soma dos n primeiros termos de uma progressão geométrica



Shaitan! De fato, .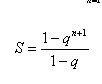

Então, finalmente, a expressão para a soma dos fundos retirados será dada como:

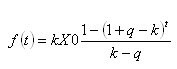
Tudo o que resta é tomar o tempo derivado e igualá-lo a zero. Sim.

 
Neutron:

Olá a todos!

Tenho permissão para usar um depósito de rublos X0 durante t meses. Todo mês o depósito recebe uma porcentagem fixa q do valor atual do depósito X. Estou autorizado a retirar mensalmente alguma porcentagem k da conta que não exceda o valor de q.

Portanto, o problema é maximizar a quantidade de dinheiro retirado durante um período de t meses.

É óbvio que a quantia a ser retirada é q e somente no final do período t. Em todos os outros casos, a quantia retirada será menor.
12345678910111213141516171819202122232425262728293031
Novo comentário