もし可能であれば、この記事の著者に以下の議論を検討してもらいたい:
今のところ、黄金比の原理は、完全な事象群を形成するフラクタル確率的連鎖を構築するのに使えると見ていますが、正直なところ、そのようなアプローチが何を与えるのかわかりません。黄金比はフィボ級数とも関連しているようですが、これもまたどのように応用できるのか、何のために応用できるのかがわかりません。もしここに書いていただけるアイデアがあれば、プラスになると思います。というわけで、一般的にこれらの過程はすでに私の頭の中で形成されており、より複雑な公式を導くのに必要なのは一般的にそれだけである。今のところ、得られたフラクタルは その役目を果たしている。そこではすべてが複雑なものから単純なものへと変化していく。黄金比の応用を考えることはできるが、それがどのように役に立つかはわからない。フィボ系列も、みんなフィボフィボと言っている.オロオロと、気の利いた言葉を聞いてオウムのように繰り返す。私はいつも、ある数学的原理が特定の問題に対応しているという事実から出発し、どんな問題でも時間が経てば必ず解を見つける。その過程で解答の道具を選び、脳自身がそれを見つけ、可能であれば耳に入ってくるものとの類似点を見つける。つまり、まず何を見つける必要があるかを判断し、それから問題を解決する方法を探すのである。具体的な問題点を聞きたいし、そのような解決策を別の記事にしても面白いし、楽しいと思う。このような問題の枠組みの中で、黄金比を応用してもいいし、その結果が本当に必要で、誰かに具体的な利益を与えるものであれば、他のどんなものでも応用できる。だから、あなたは提案を書くことができる。
もし可能であれば、この記事の著者に以下の議論を検討してもらいたい:
これは、どこにでもあるフィボとZS疑惑の陳腐な神話にすぎない......。
面白いのは、どんな鍋でも、うまくひねれば、その中にフィボも黄金 比もπもeも、その他いろいろなものが見つかるということだ......。
フィボとZSはどこにでも、どこにでもある......というのは、陳腐な神話にすぎない。
面白いのは、どんな鍋でも、よく回してみると、その中にフィボや黄金比、円周率やeの数、その他いろいろなものが見つかるということだ...。
フィーバ(これは黄金 比でもあるのだが、多くの人は気づいていない)は、きわめて簡単に探せる、つまり見ることができる。なぜならそれらは指数だからだ。一般に、学校で習った(!!)初歩的なことを非常に長く話すことはできるが、それは役に立たない。
こんな風にもできる:
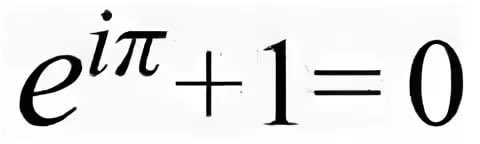
美しい、神秘的...FIBOとフーリエの関係...コップ1杯の世界定数...その他ナンセンスなこと
フィボとZSはどこにでも、どこにでもある......というのは、陳腐な神話にすぎない。
面白いのは、どんな鍋でも、よくひねってみると、その中にフィボや黄金比、円周率やeの数、その他いろいろなものを見つけることができるということだ...。
鍋を頭の上に乗せれば、鍋の中に頭と肩を見つけることもできる(笑)。
フィボやZSがどこにでもある、どこにでもあるというのは、単なるハナシに過ぎない......。
面白いのは、どんな鍋でもよくひねってみると、その中にフィボや黄金比や円周率やeやその他いろいろなものが見つかるということだ......。
本当にその通りだ。トレーダーは、何もないところに隠された意味を探すのがとても好きだ。)私も同じようなことを丁寧に伝えようとしているのですが、本当のことを言わずにどうすればいいのかわかりませんし、本当のことは残酷です。)私は、問題があり、可能な解決策があり、それ以外は時間の無駄であるという結論に達した。解決策を得るためには、まず問題を明確に設定し、その解決策の可能性について少なくとも表面的な考えを持たなければならない。もしそのような方法がなければ、上に述べたようなこと、フィボナッチ、オイラーの公式、その他非常に美しいが役に立たないゴミのようなものを始め、思わず行間を読み始めることになる。それぞれの道具にはそれぞれの仕事がある。これに関連して、私は具体的なこと(具体的な仕事)に取りかかることを提案する。
今のところ、黄金比の原理を使えば、完全な事象群を形成するフラクタル確率連鎖を構成できることはわかりましたが、このアプローチで何ができるのか、正直わかりません。黄金比はフィボ級数とも関連しているようですが、これまたどのように応用できるのか、何のために応用できるのかがわかりません。もしここに書いていただけるアイデアがあれば、プラスになると思います。というわけで、一般的にこれらの過程はすでに私の頭の中で形成されており、より複雑な公式を導くのに必要なのは一般的にそれだけである。今のところ、得られたフラクタルは その役目を果たしている。そこではすべてが複雑なものから単純なものへと変化していく。黄金比の応用を考えることはできるが、それがどのように役に立つかはわからない。フィボ系列も、みんなフィボフィボと言っている.オロオロと、気の利いた言葉を聞いてオウムのように繰り返す。私はいつも、ある数学的原理が特定の問題に対応しているという事実から出発し、どんな問題でも時間が経てば必ず解を見つける。その過程で解答の道具を選び、脳自身がそれを見つけ、可能であれば耳に入ってくるものとの類似点を見つける。つまり、まず何を見つける必要があるかを判断し、それから問題を解決する方法を探すのである。具体的な問題点を聞きたいし、そのような解決策を別の記事にしても面白いし、楽しいと思う。このような問題の枠組みの中で、黄金比を応用してもいいし、その結果が本当に必要で、誰かに具体的な利益を与えるものであれば、他のどんなものでも応用できる。だから、あなたは提案を書くことができる。
1.フィボ水準が正しく計算されていれば、フィボ水準を使うことはできますが、エリオット波動と組み合わせて使うことは勧めません。
もちろん、これがすべてではありません。この作業がいかに時間がかかり、骨の折れる作業であるかはお分かりだと思いますが、私がこのスレッドを立てたのには理由があります。正直なところ、このような問題は、研究所全体とまではいかなくても、数学者やプログラマーからなるチーム全体が対処すべきものである。 一人の人間がそれに対して何ができるだろうか?スーパーブレインがいたとしても、処理すべきデータが多すぎて頭がおかしくなりかねない。私は自分の時間と能力に見合った仕事を設定しようとしている。時間は最も貴重な資源だ。もし複雑な分析に興味があり、完全な献身を求める人がいれば、私は喜んでそれを行うだろう。とはいえ、この支部は続くだろうし、私はできる限り新しいことを伝えたいと思っている。
自然界における黄金 比の普遍性に関する神話は、人々が実際のチェックを気にすることさえなく、全体と部分の比率という考え方の美しさの魅力に屈するほど大きくなっているが、実際はそうではない:
- 軟体動物の貝殻は(通常、WDの魔法についての記事で説明されている)一般的な意見に反してWDに対応していません。
- 有名なレオナルド・ダ・ヴィンチのデッサン "Vitruvian Man "に描かれた人体のプロポーションは、実際の人間との関連では観察されない。
- パルテノン神殿、ピラミッド、その他の物体は、(神秘主義愛好家によって描かれた)RSに非常に不正確に対応している。
- EQが美の知覚の基礎であるかどうかを明らかにすることを目的とした客観的な心理学的研究は、失敗に終わっている。
- 最後に、トレーディングにおけるレベルの分解/拒否の定量的テストは、EQが特に重要なものであることを示すものでもない。
マーケットが時折(キーワードはanother time)うまくプルバック/フィボレベルをブレイクアウトできる唯一の理由は、多数のテクニカル・トレーダーがフィボレベルを集団的に信じているからである(自己成就予言)、フィボ・レベルのブレイクダウン/反転は単なるランダムかもしれないが、EQの信者にとっては、信仰の確認となることは間違いない。
スタンフォード大学の数学教授、キース・デブリンはこのことを簡単に説明する。ほとんどの人は数学を理解していないし、黄金比のような公式が複雑なシステムにどのように適用されるかすら理解できない。人々は、自然の中や自分の好きなものの中に黄金比がどこにでもあると考えるが、それを実証することはできない。彼らは、宇宙のさまざまな対象物に意味を見出そうとする自然な欲求の犠牲者なのだが、数学的リテラシーが欠如しているため、彼らが検出したパターンが幻想であることに気づくことができない。"
人は単純な説明を見つけるために自分自身(ゾンビ)をプログラムし、この信念を維持しようと努力する。これは、貿易を含む宗教的思考の本質である...
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事「取引のための組合せ論と確率論(第II部): ユニバーサルフラクタル」はパブリッシュされました:
本稿では、フラクタルの研究を続け、すべての資料の要約に特に注意を払います。これを行うために、これまでの開発をすべて、取引での実用化に便利で理解しやすいコンパクトな形にまとめてみます。
前回の記事で導出した構築ルールを使用して、フラクタルがどのように構築されるかを理解するために補足してみましょう。さらに、数式に小さな間違いがあり、境界線を下向きまたは上向きに非対称化することができませんでした。導出された式は正しいことが判明したため、どのフラクタルでも機能します。実際、これはまさにあらゆるフラクタルを実装するための関数です。考えられるすべてのフラクタルは、一般的なフラクタルの特殊なケースです。上で定義した3種類のフラクタルを使用すると、これら3つの特殊なケースを実装するための一般的なフラクタルの条件は次のようになります。
これらの3種類のフラクタルは図式的には次のようになります。
理想的には、「S」は無限大になります。次の変数は、私の以前の記事では説明されていませんでした。ここでは、一般式を使用して特殊なケースを取得する方法の全体像を把握するために、関連する説明を提示します。フラクタルは、原子爆弾のように連鎖反応の原理で機能する関数です。集合連鎖反応が深すぎると、コンピュータがそのような大規模な計算に対処できない可能性があります。ケースが特に重大でない場合は、数分、数時間、さらには数日という非常に長い時間カウントされます。
作者: Evgeniy Ilin