MQL言語を使用したゼロからのディープニューラルネットワークプログラミング

はじめに

機械学習が最近一般化しおり、多くの人がディープラーニングについて耳にし、MQL言語でそれを適用する方法を知りたいと望んでいます。活性化関数を備えた人工ニューロンの単純な実装はあるようですが、実際のディープニューラルネットワークを実装するものはありません。この記事では、MQL言語で実装されたディープニューラルネットワークと、隠れ層の双曲線正接関数や出力層のSoftmax関数などのさまざまな活性化関数を紹介します。最初から最後まで手順を追って、完全なディープニューラルネットワークを形成します。

1. 人工ニューロンの作成

それはニューラルネットワークの基本単位である単一ニューロンから始まります。この記事では、ディープニューラルネットワークで使用するニューロンの種類のさまざまな部分に焦点を当てますが、ニューロンの種類の最大の違いは通常活性化関数です。

1.1. 単一ニューロンのパーツ

人工ニューロンは人間の脳のニューロンを大まかにモデル化しており、単に数学的な計算をホストします。私たちのニューロンのように、人工ニューロンは十分な刺激に遭遇したときにトリガーされます。ニューロンは、データからの入力を、その入力を増幅または減衰する一連の係数または重みと組み合わせます。これにより、アルゴリズムが学習しようとしているタスクの入力に重要性が割り当てられます。次の画像で、動作中のニューロンの各部分を確認してください。

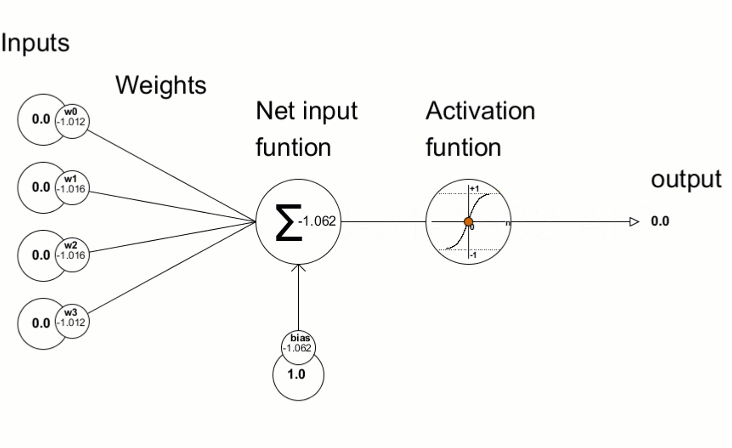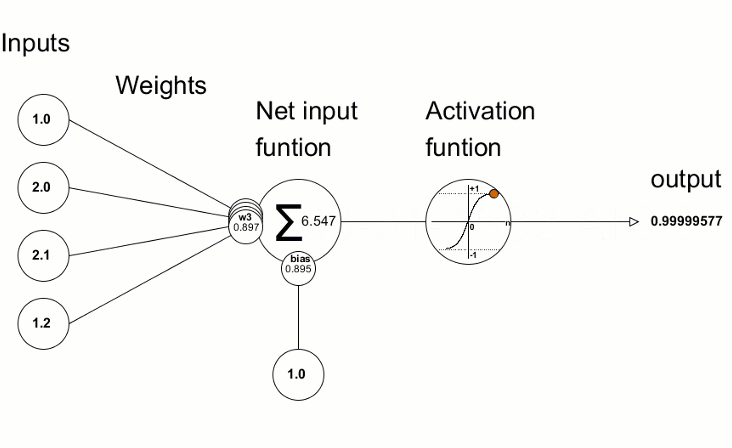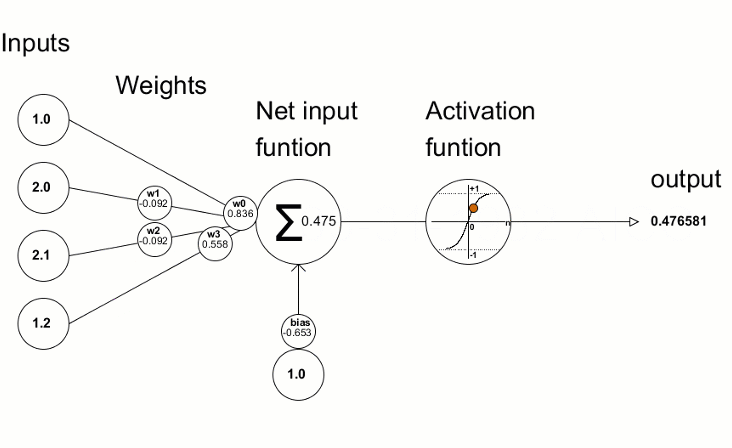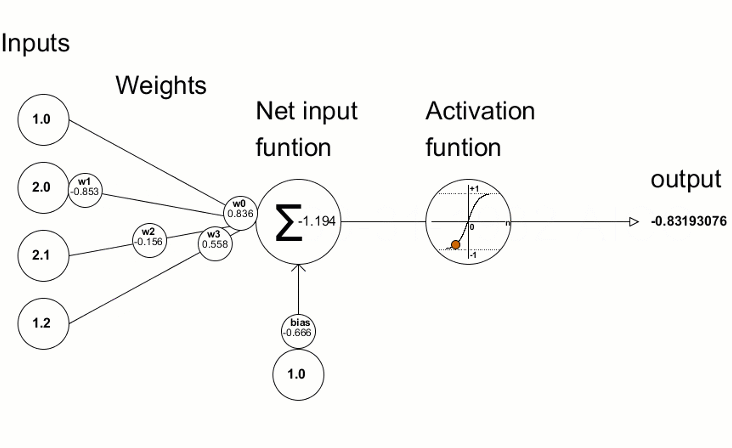
1.1.1. 入力

入力は、環境からの外部トリガーであるか他の人工ニューロンの出力からのもので、ネットワークによって評価されます。それはニューロンの「食物」として機能し、それを通過します。これにより、ニューロンに与えた訓練によって解釈できる出力になります。それらは、離散値または実数値にすることができます。

1.1.2. 重み

重みは、それらに対応するエントリで乗算される係数であり、それらの値を増減し、ニューロン内に入る入力、したがって出力に多かれ少なかれ意味を与えます。ニューラルネットワークの訓練アルゴリズムの目標は、問題を解決するための「最良の」重み値のセットを決定することです。

1.1.3. ネット入力関数

このニューロンの部分では、入力と重みは、各エントリにその重みを掛けたものの合計として、単一の結果の積に収束します。この結果または値は、活性化関数を介して渡されます。これにより、入力ニューロンがニューラルネットワークの出力に与える影響の測定値が得られます。

1.1.4. 活性化関数

活性化関数は出力につながります。活性化関数にはいくつかのタイプがあり(Sigmoid、Tan-h、Softmax、ReLUなど)、ニューロンを活性化するかどうかを決定します。この記事では、Tan-hタイプとSoftmaxタイプの関数に焦点を当てています。

1.1.5. 出力

最後に、出力があります。別のニューロンに渡すか、外部環境でサンプリングすることができます。この値は、使用される活性化関数に応じて、離散または実数になります。

2. ニューラルネットワークの構築

ニューラルネットワークは、脳などの生物学的神経系の情報処理方法に触発されています。これは人工ニューロンの層で構成されており、各層は次の層に接続されています。したがって、前の層は次の層への入力として機能し、最後には出力層への入力として機能します。ニューラルネットワークの目的は、教師なし学習によるクラスタリング、教師あり学習または回帰による分類である可能性があります。この記事では、BUY、SELL、HOLDの3つの状態に分類する機能に焦点を当てます。以下は、1つの隠れ層を持つニューラルネットワークです。

3. ニューラルネットワークからディープニューラルネットワークへのスケーリング

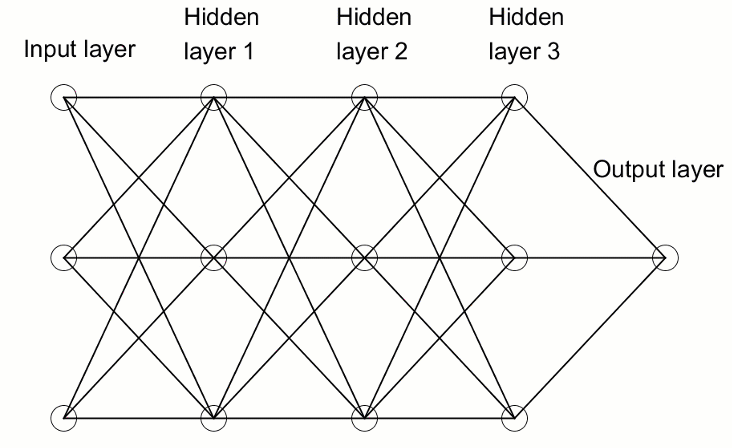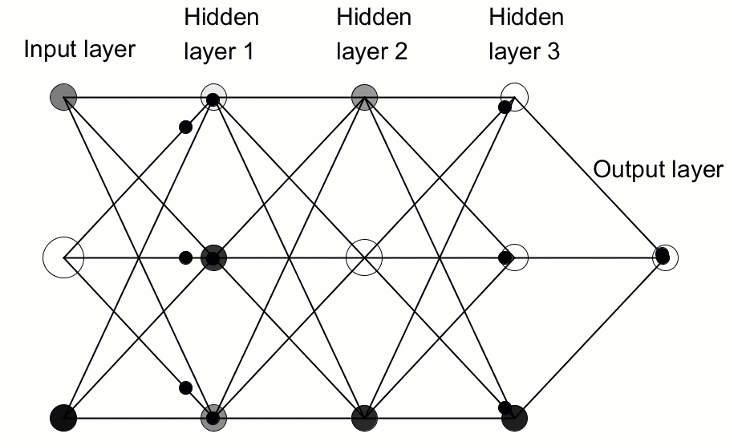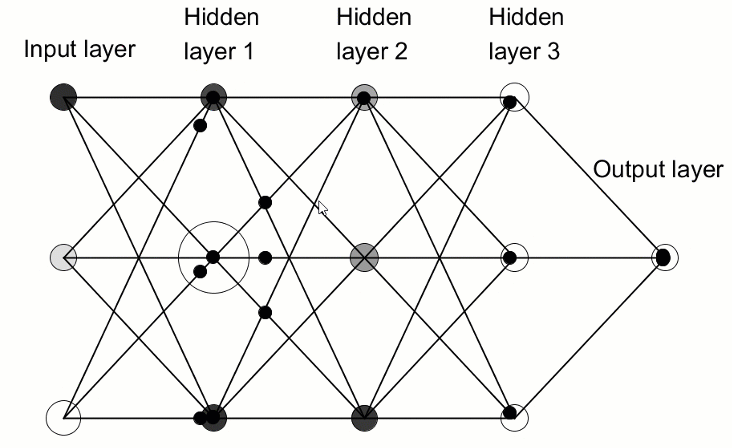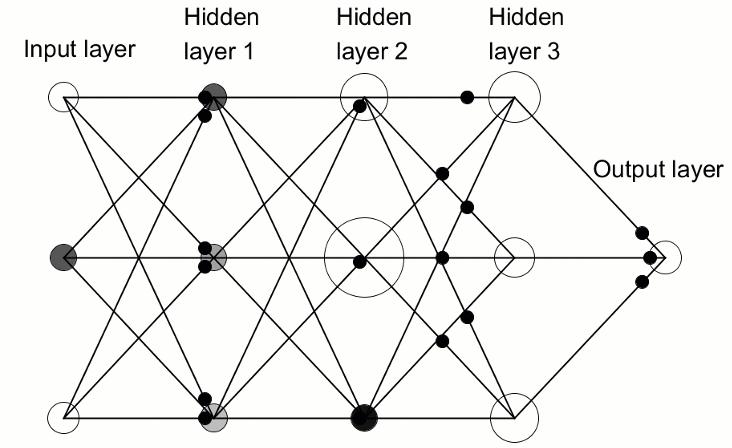
ディープニューラルネットワークをより一般的な単一の隠れ層ニューラルネットワークと区別するのは、その深さを構成する層の数です。3つ以上の層(入力と出力を含む)は、「ディープ」ラーニングと見なされます。したがって、ディープとは厳密に定義された技術用語であり、複数の隠れ層を意味します。ニューラルネットに進むほど、ニューロンが認識できる複雑な機能があります。これは、前の層の機能を集約して再結合するためです。これにより、深層学習ネットワークは、非線形関数を通過する数十億のパラメータを持つ非常に大規模で高次元のデータセットを処理できるようになります。下の画像では、3つの隠れ層を持つディープニューラルネットワークを参照してください。

3.1. ディープニューラルネットワーククラス

次に、ニューラルネットワークを作成するために使用するクラスを見てみましょう。ディープニューラルネットワークは、DeepNeuralNetworkという名前のプログラム定義クラスにカプセル化されています。主な方法は、3-4-5-3の完全に接続されたフィードフォワードニューラルネットワークをインスタンス化します。後で、この記事のディープニューラルネットワークのトレーニングセッションで、ネットワークにフィードするエントリの例をいくつか示しますが、ここでは、ネットワークの作成に焦点を当てます。ネットワークは、2つの隠れ層用にハードコーディングされています。3層以上のニューラルネットワークは非常にまれですが、より多くの層でネットワークを作成したい場合は、この記事で紹介する構造を使用して簡単に作成できます。入力から層Aへの重みは行列iaWeightsに格納され、層Aから層Bへの重みはマトリックスabWeightsに格納されます。層Bから出力への重みは行列boWeightsに格納されます。多次元配列は最初の次元でのみ静的または動的であり、それ以降のすべての次元は静的であるため、行列のサイズは「#define」ステートメントを使用して定数変数として宣言されます。スペースを節約するために最上位のSystem名前空間を参照するステートメントを除いたすべてのusingステートメントを削除しました。完全なソースコードは、記事の添付ファイルにあります。

以下はプログラムの構造です。

#define SIZEI 4
#define SIZEA 5
#define SIZEB 3
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class DeepNeuralNetwork
  {
private:

   int               numInput;
   int               numHiddenA;
   int               numHiddenB;
   int               numOutput;

   double            inputs[];

   double            iaWeights[][SIZEI];
   double            abWeights[][SIZEA];
   double            boWeights[][SIZEB];

   double            aBiases[];
   double            bBiases[];
   double            oBiases[];

   double            aOutputs[];
   double            bOutputs[];
   double            outputs[];

public:

                     DeepNeuralNetwork(int _numInput,int _numHiddenA,int _numHiddenB,int _numOutput)
     {...}
     

   void SetWeights(double &weights[])
     {...}      
    

   void ComputeOutputs(double &xValues[],double &yValues[])
     {...}     
          

   double HyperTanFunction(double x)
     {...}      
     

   void Softmax(double &oSums[],double &_softOut[])
     {...}
      

  };
//+------------------------------------------------------------------+

2つの非表示層と1つの出力層には、それぞれaBiases、bBiases、oBiasesという名前の関連するバイアス値の配列があります。非表示層のローカル出力は、aOutputsおよびbOutputsという名前のクラススコープ配列に格納されます。

3.2. ディープニューラルネットワーク出力の計算

ComputeOutputsメソッドではまず、予備的な(アクティブ化前の)合計を保持するようにスクラッチ配列を設定します。次に、重みの予備的な合計にA層ノードの入力を乗算したものを計算し、バイアス値を加算してから、活性化関数を適用します。次に、計算されたばかりの層A出力をローカル入力として使用して、層Bローカル出力が計算され、最後に最終出力が計算されます。

void ComputeOutputs(double &xValues[],double &yValues[])
     {
      double aSums[]; // hidden A nodes sums scratch array
      double bSums[]; // hidden B nodes sums scratch array
      double oSums[]; // output nodes sums

      ArrayResize(aSums,numHiddenA);
      ArrayFill(aSums,0,numHiddenA,0);
      ArrayResize(bSums,numHiddenB);
      ArrayFill(bSums,0,numHiddenB,0);
      ArrayResize(oSums,numOutput);
      ArrayFill(oSums,0,numOutput,0);

      int size=ArraySize(xValues);

      for(int i=0; i<size;++i) // copy x-values to inputs
         this.inputs[i]=xValues[i];

      for(int j=0; j<numHiddenA;++j) // compute sum of (ia) weights * inputs
         for(int i=0; i<numInput;++i)
            aSums[j]+=this.inputs[i]*this.iaWeights[i][j]; // note +=

      for(int i=0; i<numHiddenA;++i) // add biases to a sums
         aSums[i]+=this.aBiases[i];

      for(int i=0; i<numHiddenA;++i) // apply activation
         this.aOutputs[i]=HyperTanFunction(aSums[i]); // hard-coded

      for(int j=0; j<numHiddenB;++j) // compute sum of (ab) weights * a outputs = local inputs
         for(int i=0; i<numHiddenA;++i)
            bSums[j]+=aOutputs[i]*this.abWeights[i][j]; // note +=

      for(int i=0; i<numHiddenB;++i) // add biases to b sums
         bSums[i]+=this.bBiases[i];

      for(int i=0; i<numHiddenB;++i) // apply activation
         this.bOutputs[i]=HyperTanFunction(bSums[i]); // hard-coded

      for(int j=0; j<numOutput;++j) // compute sum of (bo) weights * b outputs = local inputs
         for(int i=0; i<numHiddenB;++i)
            oSums[j]+=bOutputs[i]*boWeights[i][j];

      for(int i=0; i<numOutput;++i) // add biases to input-to-hidden sums
         oSums[i]+=oBiases[i];

      double softOut[];
      Softmax(oSums,softOut); // softmax activation does all outputs at once for efficiency
      ArrayCopy(outputs,softOut);

      ArrayCopy(yValues,this.outputs);

     }

舞台裏では、ニューラルネットワークは2つの隠れ層の出力を計算するときには双曲線正接活性化関数(Tan-h)を使用し、最終的な出力値を計算するときにはSoftmax活性化関数を使用します。

• 双曲線正接(Tan-h): ロジスティックシグモイドと同様、Tan-h関数もシグモイドですが、代わりに(-1、1)の範囲の値を出力します。したがって、Tan-hへの非常に負の入力は、負の出力にマッピングされます。さらに、ゼロ値の入力のみがゼロに近い出力にマップされます。この場合、数式だけでなく、MQLソースコードでの実装も示します。

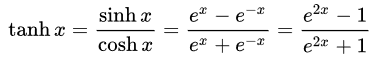
   double HyperTanFunction(double x)
     {
      if(x<-20.0) return -1.0; // approximation is correct to 30 decimals
      else if(x > 20.0) return 1.0;
      else return MathTanh(x); //Use explicit formula for MQL4 (1-exp(-2*x))/(1+exp(-2*x))
     }

• Softmax: 複数のクラスの場合、各クラスに小数確率を割り当てます。これらの小数確率は1.0を追加する必要があります。この追加の制限により、訓練をより速く収束させることができます。

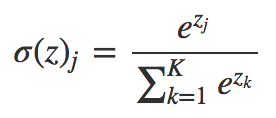
   void Softmax(double &oSums[],double &_softOut[])
     {
      // determine max output sum
      // does all output nodes at once so scale doesn't have to be re-computed each time
      int size=ArraySize(oSums);
      double max= oSums[0];
      for(int i = 0; i<size;++i)
         if(oSums[i]>max) max=oSums[i];

      // determine scaling factor -- sum of exp(each val - max)
      double scale=0.0;
      for(int i= 0; i<size;++i)
         scale+= MathExp(oSums[i]-max);

      ArrayResize(_softOut,size);
      for(int i=0; i<size;++i)
         _softOut[i]=MathExp(oSums[i]-max)/scale;

     }

4. DeepNeuralNetworkクラスを使用したデモエキスパートアドバイザー

エキスパートアドバイザーの開発を始める前に、DeepNeuralNetworkに供給されるデータを定義する必要があります。ニューラルネットワークはパターンの分類に優れているため、日本製のローソク足の相対値を入力として使用します。これらの値は、上部の髭、実体、下部の髭のサイズ、およびローソク足の方向(強気または弱気)になります。エントリ数は必ずしも少なくなくてもかまいませんが、この場合はテストプログラムとしては十分です。

デモエキスパートアドバイザー:

構造4-4-5-3ニューラルネットワークには、合計(4 * 4)+ 4 +(4 * 5)+ 5 +(5 * 3)+ 3 = 63の重みとバイアス値が必要です。

#include <DeepNeuralNetwork.mqh> 

int numInput=4;
int numHiddenA = 4;
int numHiddenB = 5;
int numOutput=3;

DeepNeuralNetwork dnn(numInput,numHiddenA,numHiddenB,numOutput);


//--- weight & bias values
input double w0=1.0;
input double w1=1.0;
input double w2=1.0;
input double w3=1.0;
input double w4=1.0;
input double w5=1.0;
input double w6=1.0;
input double w7=1.0;
input double w8=1.0;
input double w9=1.0;
input double w10=1.0;
input double w11=1.0;
input double w12=1.0;
input double w13=1.0;
input double w14=1.0;
input double w15=1.0;
input double b0=1.0;
input double b1=1.0;
input double b2=1.0;
input double b3=1.0;
input double w40=1.0;
input double w41=1.0;
input double w42=1.0;
input double w43=1.0;
input double w44=1.0;
input double w45=1.0;
input double w46=1.0;
input double w47=1.0;
input double w48=1.0;
input double w49=1.0;
input double w50=1.0;
input double w51=1.0;
input double w52=1.0;
input double w53=1.0;
input double w54=1.0;
input double w55=1.0;
input double w56=1.0;
input double w57=1.0;
input double w58=1.0;
input double w59=1.0;
input double b4=1.0;
input double b5=1.0;
input double b6=1.0;
input double b7=1.0;
input double b8=1.0;
input double w60=1.0;
input double w61=1.0;
input double w62=1.0;
input double w63=1.0;
input double w64=1.0;
input double w65=1.0;
input double w66=1.0;
input double w67=1.0;
input double w68=1.0;
input double w69=1.0;
input double w70=1.0;
input double w71=1.0;
input double w72=1.0;
input double w73=1.0;
input double w74=1.0;
input double b9=1.0;
input double b10=1.0;
input double b11=1.0;

ニューラルネットワークの入力では、次の式を使用して、ローソク足のサイズの合計を考慮して、ローソク足の各部分を表すパーセンテージを決定します。

//+------------------------------------------------------------------+
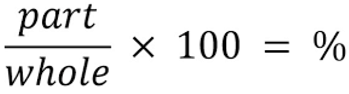
//|percentage of each part of the candle respecting total size       |
//+------------------------------------------------------------------+
int CandlePatterns(double high,double low,double open,double close,double uod,double &xInputs[])
  {
   double p100=high-low;//Total candle size   
   double highPer=0;
   double lowPer=0;
   double bodyPer=0;
   double trend=0;

   if(uod>0)
     {
      highPer=high-close;
      lowPer=open-low;
      bodyPer=close-open;
      trend=1;

     }
   else
     {
      highPer=high-open;
      lowPer=close-low;
      bodyPer=open-close;
      trend=0;
     }
   if(p100==0)return(-1);
   xInputs[0]=highPer/p100;
   xInputs[1]=lowPer/p100;
   xInputs[2]=bodyPer/p100;
   xInputs[3]=trend;

   return(1);

  }

これで、ニューラルネットワークを介して入力を処理できます。

   MqlRates rates[];
   ArraySetAsSeries(rates,true);
   int copied=CopyRates(_Symbol,0,1,5,rates);

   //Compute the percent of the upper shadow, lower shadow and body in base of sum 100%
   int error=CandlePatterns(rates[0].high,rates[0].low,rates[0].open,rates[0].close,rates[0].close-rates[0].open,_xValues);

   if(error<0)return;
   
   dnn.SetWeights(weight);

   double yValues[];
   dnn.ComputeOutputs(_xValues,yValues);

次に、ニューラルネットワークの計算に基づいて取引機会が処理されます。Softmax関数は、100％の合計に基づいて3つの出力を生成することを忘れないでください。値は配列「yValues」に格納され、60％を超える値が実行されます。

//--- if the output value of the neuron is mare than 60%
   if(yValues[0]>0.6)
     {
      if(m_Position.Select(my_symbol))//check if there is an open position
        {
         if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol);//Close the opposite position if exists
         if(m_Position.PositionType()==POSITION_TYPE_BUY) return;
        }
      m_Trade.Buy(lot_size,my_symbol);//open a Long position
     }
//--- if the output value of the neuron is mare than 60%
   if(yValues[1]>0.6)
     {
      if(m_Position.Select(my_symbol))//check if there is an open position
        {
         if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol);//Close the opposite position if exists
         if(m_Position.PositionType()==POSITION_TYPE_SELL) return;
        }
      m_Trade.Sell(lot_size,my_symbol);//open a Short position
     }

   if(yValues[2]>0.6)
     {
      m_Trade.PositionClose(my_symbol);//close any position

     }

5. ストラテジーの最適化を使用したディープニューラルネットワークの訓練

お気づきかもしれませんが、ディープニューラルネットワークのフィードフォワードメカニズムのみが実装されており、訓練は実行されません。このタスクはストラテジーテスターのために予約されています。以下に、ニューラルネットワークを訓練する方法を示します。入力数が多く、訓練パラメータの範囲が広いため、MetaTrader 5でのみ訓練できますが、最適化の値を取得すると、MetaTrader 4に簡単にコピーできます。

ストラテジーテスターの構成:

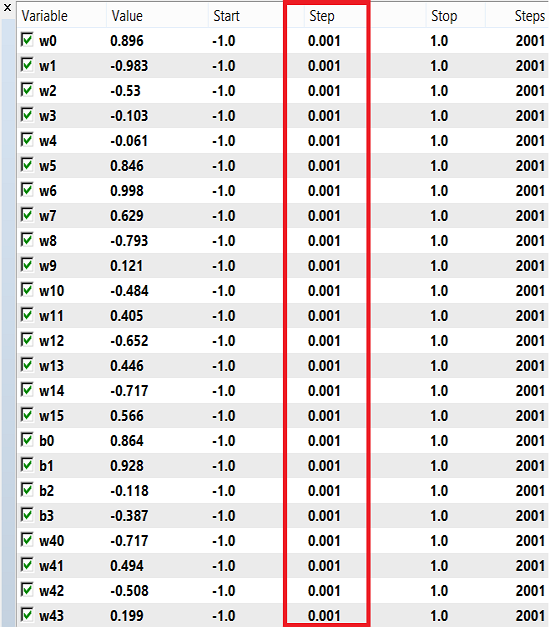
重みとバイアスは、-1から1までの範囲の数値を訓練に使用でき、ステップは0.1、0.01、または0.001です。これらの値を試して、どれが最良の結果を得るかを確認できます。私の場合、下の画像に示すように、ステップに0.001を使用しました。

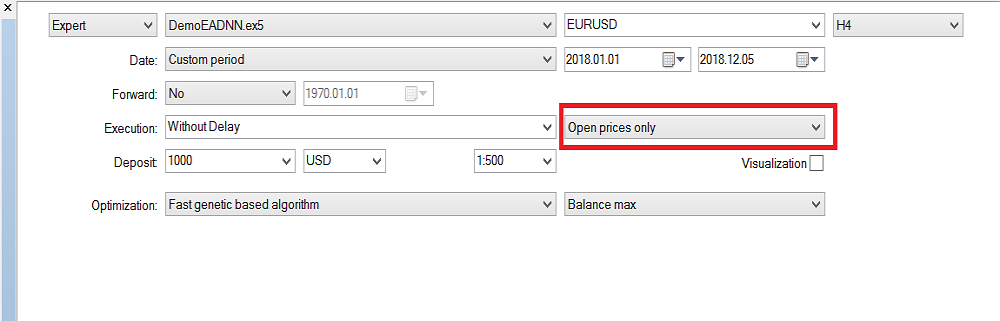
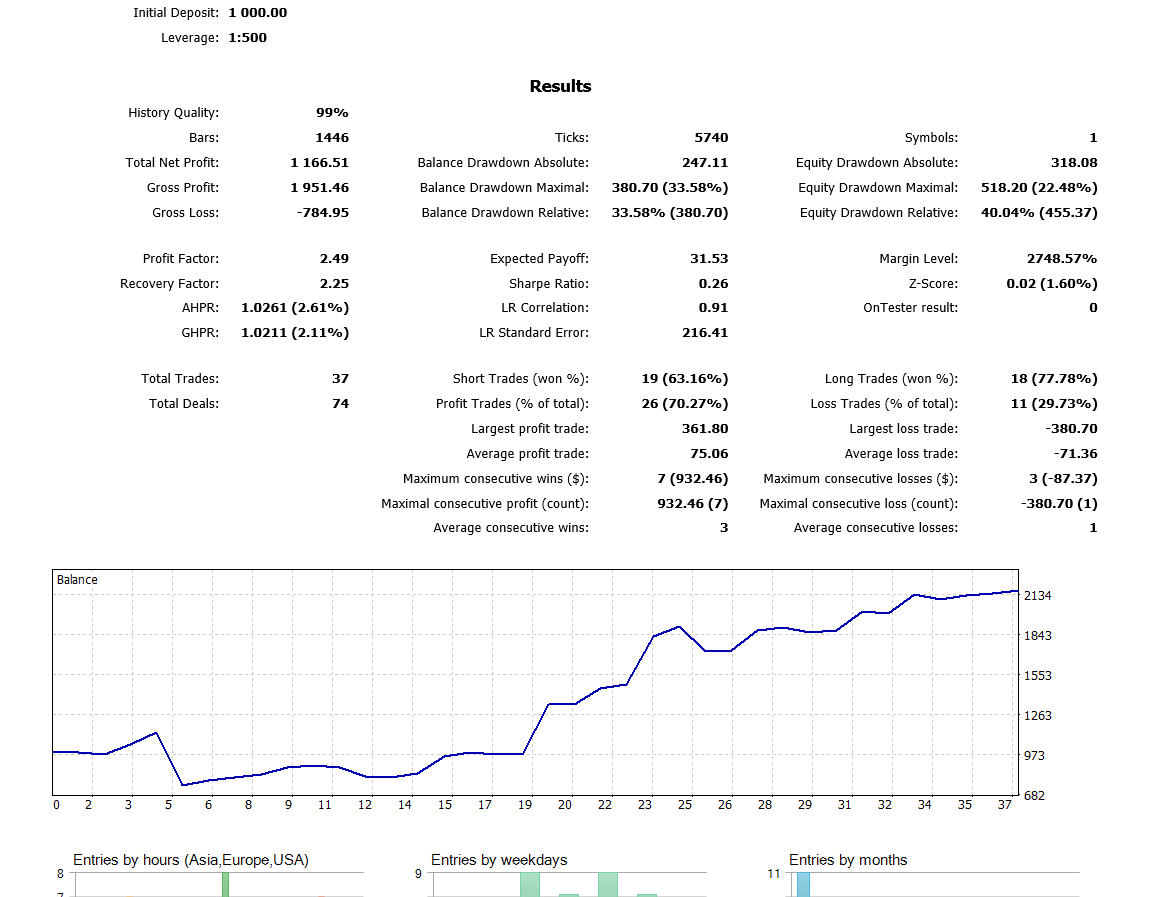
最後の閉じたローソク足を使用しているため、「始値のみ」を使用しています。すべてのティックで実行する価値はありません。現在、H4の時間枠で最適化を実行しており、昨年はバックテストで次の結果が得られました。

終わりに

この記事で紹介するコードと説明は、2つの隠れ層を持つニューラルネットワークを理解するための優れた基礎となるはずです。3つ以上の隠し層はどうでしょうか。研究文献は、ほとんどすべての実際的な問題には2つの隠れた層で十分であるということに同意しています。この記事では、ディープニューラルネットワークを使用して改善された為替レート予測モデルを開発するためのアプローチの概要を説明しています。これは、ディープネットワークが生データから抽象的な特徴を学習する機能に動機付けられています。予備的な結果によって、私たちのディープネットワークが、先進国の通貨市場のベースラインモデルよりも大幅に高い予測精度を生み出すことが確認されています。