El enfoque econométrico en la búsqueda de leyes de mercado: autocorrelación, mapas de calor y diagramas de dispersión

Breve panorámica de los materiales anteriores y prerrequisitos para crear el nuevo modelo

En el primer artículo, ya vimos el concepto de "memoria del mercado", que se define como la dependencia a largo plazo de los incrementos de precio de cierto orden. Acto seguido, analizamos el concepto de " leyes estacionales", que, en uno u otro aspecto, están presentes en el mercado. Hasta este momento, estos dos conceptos existían por separado y no se cruzaban en ninguna parte. El objetivo de este artículo es mostrar que la "memoria del mercado" tiene un carácter estacional que se muestra a través de la maximización de la correlación de los incrementos de orden aleatorio para los intervalos temporales próximos, y la minimización de la correlación para los intervalos temporales alejados unos de otros, respectivamente.

Vamos a expresar la teoría, que sonará, aproximadamente, en los términos que siguen:

La correlación de los incrementos se basa en la presencia de ciertas regularidades y leyes estacionales, así como en el agrupamiento (clusterización) de los incrementos que se encuentran próximos. 

Una hipótesis atrevida que vamos analizar etapa por etapa para, ya sea para confirmarla o para refutarla en un estilo intuitivo y un tanto matemático.

El enfoque econométrico clásico en cuanto a la detección de leyes en los incrementos de precio es precisamente la autocorrelación.

El enfoque clásico presupone que la ausencia de leyes en los incrementos de precio se determina a través de la ausencia de una correlación serial. En el caso de que no exista correlación, la serie de incrementos se considerará casual, y la posterior búsqueda de leyes resultará ineficaz. 

Ilustraremos este hecho usando como ejemplo el análisis de la autocorrelación de la función de incremento de la pareja de divisas EURUSD. Para los experimentos, utilizaremos IPython.

def standard_autocorrelation(symbol, lag):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    rates = rates.diff(lag).dropna()
    from pandas.plotting import autocorrelation_plot
    plt.figure(figsize=(10, 5))
    autocorrelation_plot(rates)

standard_autocorrelation('EURUSD', 50)

Esta función transforma los precios por hora de cierre en su diferencia con el periodo establecido (usaremos un lag de 50), y representa el gráfico de autocorrelación.

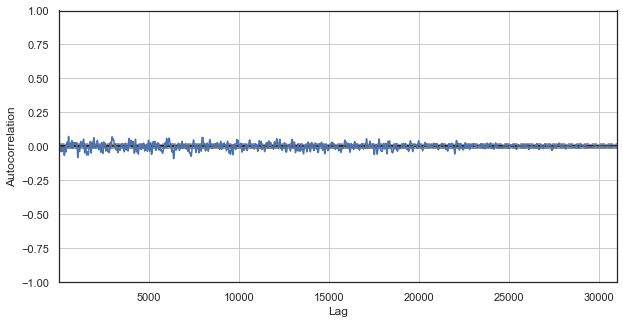
Fig. 1. Correlograma clásico de incrementos de precio

El gráfico de correlaciones no detecta ninguna ley en los incrementos de precio. Las correlaciones entre incrementos colindantes oscilan en torno al cero, lo que presupone la aleatoriedad de la serie temporal. Con esto, podríamos dar por finalizado el análisis econométrico y afirmar orgullosamente que el mercado es puro azar. Sin embargo, proponemos mirar a la autocorrelación desde otro ángulo: en el contexto de las leyes estacionales.

Dado que hemos supuesto que la correlación de incrementos de precio se genera con la presencia de leyes estacionales, para que el experimento sea lo más puro posible, vamos a excluir de la serie todas las horas salvo una concreta. De esta manera, crearemos una nueva serie temporal que poseerá sus propiedades únicas. Vamos a crear una función de autocorrelación para ella:

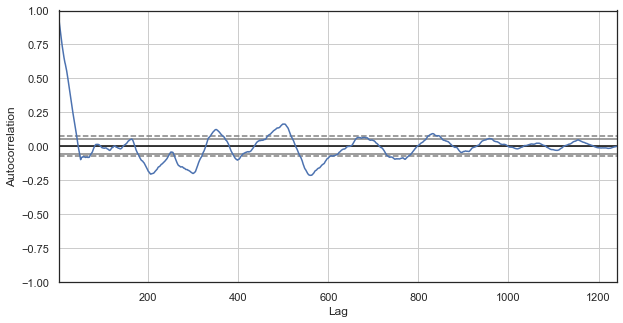
Fig. 2. Correlograma de incrementos de precio con horas excluidas (solo hemos dejado la primera hora para cada día)

Para la nueva serie, el correlograma parece más interesante. Podemos observar una fuerte dependencia de los incrementos actuales respecto a los anteriores, que se reduce con el aumento de la delta temporal entre incrementos. De esta forma, el incremento de la primera hora del día actual se correlaciona fuertemente con el incremento de la primera hora del día anterior, y así sucesivamente, en orden descendente. Esta es una iniformación muy importante, e indica la existencia de leyes estacionales: los incrementos poseen claramente memoria.

El enfoque personalizado en cuanto a la detección de leyes en los incrementos de precio es precisamente la autocorrelación estacional.

Seguramente, habremos convencido al lector de la existencia de leyes estacionales, y más concretamente, de la correlación entre los incrementos de precio de la primera hora del día presente y la primera hora de los días anteriores, que disminuye conforme aumenta la delta (distancia en días). Ahora, vamos a analizar si existe una dependencia entre las horas colindantes. Para ello, modificaremos un poco el código:

def seasonal_autocorrelation(symbol, lag, hour1, hour2):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 
    rates = rates.drop(rates.index[~rates.index.hour.isin([hour1, hour2])]).diff(lag).dropna()
    from pandas.plotting import autocorrelation_plot
    plt.figure(figsize=(10, 5))
    autocorrelation_plot(rates)

seasonal_autocorrelation('EURUSD', 50, 1, 2)

Aquí, eliminamos de las cotizaciones todas las horas salvo la primera y la segunda. Después obtenemos las diferencias para la nueva serie y construimos la función de autocorrelación:

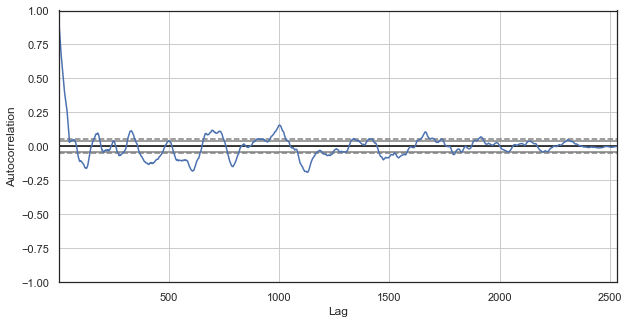
Fig. 3. Correlograma de incrementos de precio con horas excluidas (solo hemos dejado la primera y la segunda hora para cada día)

También se observa una alta correlación para la serie compuesta de las horas más próximas, lo cual indica su dependencia e influencia mutua. ¿Y qué debemos hacer si queremos obtener una valoración relativa fiable para todos los pares de horas, y no solo para las seleccionadas? Para ello, usaremos una técnica que explicaremos más abajo.

Mapa de calor de las correlaciones estacionales para todas las horas

Vamos a continuar analizando el mercado con la esperanza de confirmar la hipótesis inicial. En primer lugar, echaremos un vistazo a la imagen global. La función que mostramos más abajo elimina consecutivamente las horas de la serie temporal, dejando solo una hora. Luego construye la diferencia de precios para esta serie y determina la correlación con las series construidas para otras horas:

#calculate correlation heatmap between all hours
def correlation_heatmap(symbol, lag, corrthresh):
    out = pd.DataFrame()
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time') 

    for i in range(24):
        ratesH = None
        ratesH = rates.drop(rates.index[~rates.index.hour.isin([i])]).diff(lag).dropna()
        out[str(i)] = ratesH['close'].reset_index(drop=True)
    plt.figure(figsize=(10, 10))
    corr = out.corr()
    # Generate a mask for the upper triangle
    mask = np.zeros_like(corr, dtype=np.bool)
    mask[np.triu_indices_from(mask)] = True
    sns.heatmap(corr[corr >= corrthresh], mask=mask)
    return out

out = correlation_heatmap(symbol='EURUSD', lag=25, corrthresh=0.9)    

La función adopta el orden de los incrementos (lag temporal), así como el umbral de correlación para el cribado de las horas con baja correlación. Veamos qué resulta:

Fig. 4. Mapa de calor de las correlaciones entre incrementos para diferentes horas en el periodo 2015-2020.

Se ven claramente los clústeres de las horas 0-5 y 10-14, donde la correlación es máxima. Recordemos que en el artículo anterior se construyó un sistema comercial de acuerdo con el primer clúster, que fue detectado con otro método (con la ayuda de boxplots). Ahora, las regularidades también se pueden ver en el mapa de calor. Vamos a tomar el segundo clúster interesante y realizar las manipulaciones posteriores con el mismo. Por ejemplo, podemos analizar la estadística resumida del clúster:

out[['10','11','12','13','14']].describe()

	10	11	12	13
count	1265.000000	1265.000000	1265.000000	1265.000000	1265.000000
mean	-0.001016	-0.001015	-0.001005	-0.000992	-0.000999
std	0.024613	0.024640	0.024578	0.024578	0.024511
min	-0.082850	-0.084550	-0.086880	-0.087510	-0.087350
25%	-0.014970	-0.015160	-0.014660	-0.014850	-0.014820
50%	-0.000900	-0.000860	-0.001210	-0.001350	-0.001280
75%	0.013460	0.013690	0.013760	0.014030	0.013690
max	0.082550	0.082920	0.085830	0.089030	0.086260

Los parámetros de todas las horas del clúster se encuentran bastante próximos, pero, y esto es más interesante, para la muestra investigada, su media es negativa (alrededor de 100 puntos de cinco dígitos). El desplazamiento del incremento medio indica una alta probabilidad de que el mercado disminuya en estas horas, antes que aumente. Conviene destacar también que un aumento del lag de incremento puede provocar una mayor correlación entre las horas debido a la aparición del componente de tendencia, mientras que una disminución del lag provocará la reducción de los indicadores. En este caso, además, con respecto a la ubicación de los clústeres, permanece prácticamente inalterable. 

Por ejemplo, para un lag de incremento único, las horas 12, 13 y 14 siguen estando fuertemente correlacionadas:

plt.figure(figsize=(10,5))
plt.plot(out[['12','13','14']])
plt.legend(out[['12','13','14']])
plt.show()

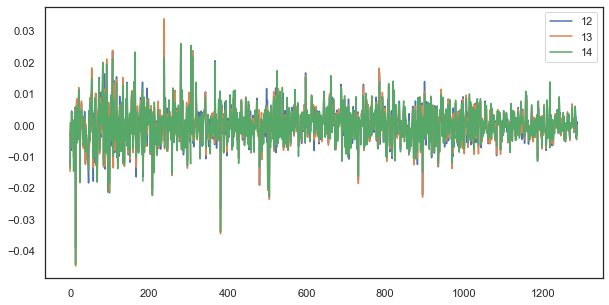
Fig. 5. Semejanza virtual de las series de incremento de lag único compuestas a partir de diferentes horas del día

La fórmula de las leyes: simple y elegante

Recordemos nuestra hipótesis:

La correlación de los incrementos se basa en la presencia de ciertas regularidades y leyes estacionales, así como en el agrupamiento (clusterización) de los incrementos que se encuentran próximos. 

En el diagrama de la función de autocorrección y en el mapa de calor hemos mostrado que existe una dependencia de los incrementos de precio tanto con los valores pasados, como con los valores de los incrementos de las horas más próximas. El primer fenómeno proviene de la capacidad de repetición de un evento en determinadas horas del día; el segundo, de la clusterización de la volatilidad en ciertos periodos de tiempo. Ambos fenómenos deben analizarse por separado y, dentro de lo posible, combinarse. En el presente artículo, vamos a realizar un análisis adicional de la dependencia de los incrementos de una hora concreta (eliminando las demás horas de la serie temporal) con respecto a los valores anteriores, mientras que dejamos lo más "jugoso" para el próximo artículo.

# calculate joinplot between real an predicted returns
def hourly_signals_statistics(symbol, lag,  hour, hour2, rfilter):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
# price differenсes for every hour series   
    H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True).diff(lag).dropna()
    H2 = rates.drop(rates.index[~rates.index.hour.isin([hour2])]).reset_index(drop=True).diff(lag).dropna()
# current returns for both hours    
    HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True)     
# previous returns for both hours    
    HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True)  
    
# Basic equation:  ret[-1] = ret[0] - (ret[lag] - ret[lag-1])
# or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) 

    predicted = HF-(HF2-HL2)
    real = HL 
# correlation joinplot between two series    
    outcorr = pd.DataFrame()
    outcorr['Hour ' + str(hour)] = H['close']
    outcorr['Hour ' + str(hour2)] = H2['close']
# real VS predicted prices     
    out = pd.DataFrame()
    out['real'] = real['close']
    out['predicted'] = predicted['close']
    out = out.loc[((out['predicted'] >= rfilter) | (out['predicted'] <=- rfilter))]
# plptting results    
    from scipy import stats
    sns.jointplot(x='Hour ' + str(hour), y='Hour ' + str(hour2), data=outcorr, kind="reg", height=7, ratio=6).annotate(stats.pearsonr) 
    sns.jointplot(x='real', y='predicted', data=out, kind="reg", height=7, ratio=6).annotate(stats.pearsonr)

hourly_signals_statistics('EURUSD', lag=25, hour=13, hour2=14, rfilter=0.00)

Vamos a aclarar la manipulación de los datos usando el listado anteriormente propuesto. Tomamos dos series formadas mediante el cribado de las horas sobrantes y construimos los incrementos de precio (sus diferencias). Las horas para las series se determinan en los parámetros "hour" y "hour2". A continuación, obtenemos las secuencias con el lag 1 para cada hora, en otras palabras, la serie " HF" se anticipa a la serie "HL" en un valor, lo cual es necesario para calcular el incremento factual y el incremento pronosticado, así como sus diferencias. Primero construimos el diagrama de dispersión para los incrementos de la primera y la segunda hora:

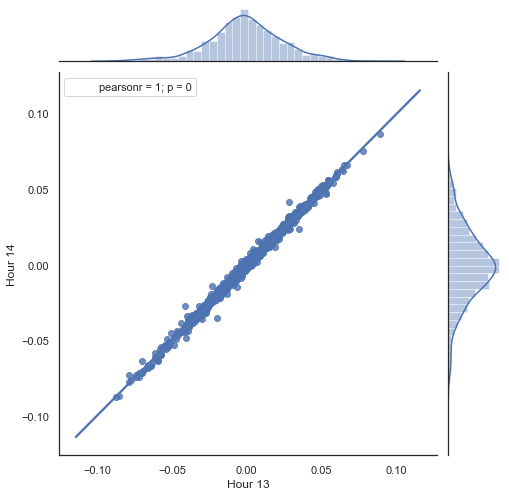
Fig. 5. Diagrama de dispersión para los incrementos de las horas 13 y 14 en el periodo 2015-2020.

Como era de esperar, los incrementos tienen una correlación fuerte. Ahora, vamos a pronosticar el siguiente incremento basándonos en el anterior. Para ello, mostraremos una sencilla fórmula que pronosticará el siguiente incremento:

Basic equation:  ret[-1] = ret[0] - (ret[lag] - ret[lag-1])

or Close[-1] = (Close[0]-Close[lag]) - ((Close[lag]-Close[lag*2]) - (Close[lag-1]-Close[lag*2-1])) 

Vamos a analizar la fórmula obtenida. Para pronosticar el futuro incremento, nos encontramos en la barra cero, por consiguiente, pronosticamos el valor del siguiente incremento ret[-1]. Para ello, deberemos restar al incremento actual la diferencia entre el incremento anterior (con un retraso lag) y el siguiente (lag-1). Si la correlación de los incrementos entre dos horas colindantes es alta, podemos esperar que el incremento pronosticado se describa con esta ecuación. Más abajo se muestra simplemente la ecuación para los precios de cierre. Como conclusión, en el pronóstico del futuro incremento toman parte un total de 3 incrementos. La segunda parte del código del listado ofrecido precisamente pronostica los futuros incrementos según la fórmula y los compara con los reales. Vamos a ilustrar este momento en el diagrama:

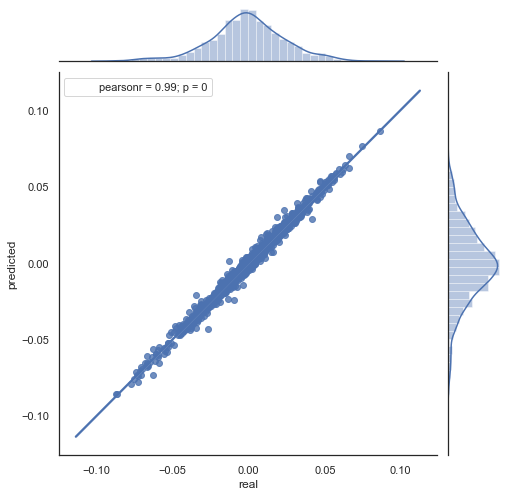
Fig. 6. Diagrama de dispersión para los incrementos reales y pronosticados en el periodo 2015-2020.

Se ve perfectamente que los gráficos en las figuras 5,6 son semejantes. Esto indica que el método de definición de regularidades usando la correlación ha superado la prueba y es válido. Al mismo tiempo, en el diagrama se ve la dispersión de los valores, que no se encuentran en una misma línea. Estos son los errores de pronóstico, que influirán negativamente en el mismo; trabajaremos con ellos aparte (dicho punto no entra en el marco del presente artículo). Además, un pronóstico alrededor del cero apenas nos interesa: si el pronóstico del incremento del próximo precio es igual al actual, no ganaremos dinero con ello. Podemos filtrar los pronósticos con la ayuda del parámetro rfilter.

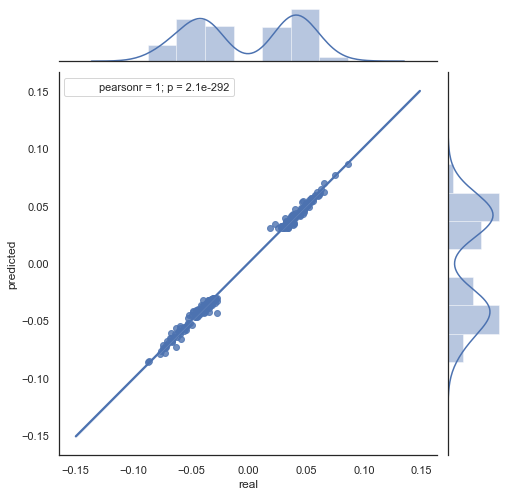
Fig. 7. Diagrama de dispersión para los incrementos reales y pronosticados con rfilter = 0.03 en el periodo 2015-2020.

Debemos destacar que el mapa de calor mostrado se ha construido en un periodo que abarca desde 2015 hasta el día presente. Vamos a retroceder 15 años y analizar el fragmento que va desde el año 2000 hasta este momento:

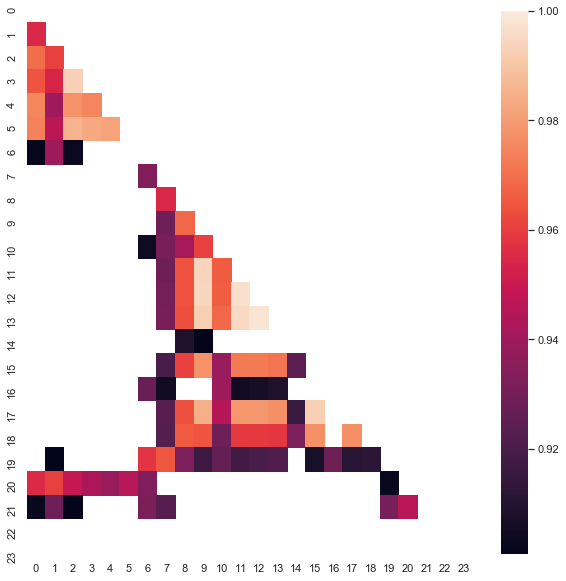
Fig. 8. Mapa de calor de las correlaciones entre incrementos para diferentes horas en el periodo 2000-2020.

	10	11	12	13
count	5151.000000	5151.000000	5151.000000	5151.000000	5151.000000
mean	0.000470	0.000470	0.000472	0.000472	0.000478
std	0.037784	0.037774	0.037732	0.037693	0.037699
min	-0.221500	-0.227600	-0.222600	-0.221100	-0.216100
25%	-0.020500	-0.020705	-0.020800	-0.020655	-0.020600
50%	0.000100	0.000100	0.000150	0.000100	0.000250
75%	0.023500	0.023215	0.023500	0.023570	0.023420
max	0.213700	0.212200	0.210700	0.212600	0.208800

Podemos ver que el mapa de calor muestra algo menos de frecuencia en sus valores: la dependencia entre las horas 13 y 14 ha disminuido. Al mismo tiempo, el incremento medio es ahora positivo, lo cual da prioridad a las compras sobre las ventas. El desplazamiento de la media no permite comerciar de forma eficaz en ambos intervalos temporales, así que tendremos que elegir.

Vamos a ver el diagrama de dispersión obtenido en este periodo (nos limitaremos al gráfico de hecho\pronóstico):

Fig. 9. Diagrama de dispersión para los incrementos reales y pronosticados con rfilter = 0.03 en el periodo 2000-2020.

La dispersión de los valores ha aumentado, lo cual no indica un resultado positivo en un periodo tan largo.

De esta forma, hemos conseguido obtener una fórmula, además de una imagen aproximada sobre las distribuciones y los pronósticos de los incrementos para unas horas concretas. Para que resulte más clara, podemos visualizar la dependencia en 3D.

# calculate joinplot between real an predicted returns
def hourly_signals_statistics3D(symbol, lag,  hour, hour2, rfilter):
    rates = pd.DataFrame(MT5CopyRatesRange(symbol, MT5_TIMEFRAME_H1, datetime(2015, 1, 1), datetime(2020, 1, 1)), 
                         columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
    rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1).set_index('time')
    rates = pd.DataFrame(rates['close'].diff(lag)).dropna()
    
    out = pd.DataFrame();
    for i in range(hour, hour2):
        H = None; H2 = None; HF = None; HL = None; HF2 = None; HL2 = None; predicted = None; real = None;
        H = rates.drop(rates.index[~rates.index.hour.isin([hour])]).reset_index(drop=True)
        H2 = rates.drop(rates.index[~rates.index.hour.isin([i+1])]).reset_index(drop=True)
        HF = H[1:].reset_index(drop=True); HL = H2[1:].reset_index(drop=True);     # current hours
        HF2 = H[:-1].reset_index(drop=True); HL2 = H2[:-1].reset_index(drop=True)  # last day hours
    
        predicted = HF-(HF2-HL2)
        real = HL 
    
        out3D = pd.DataFrame()
        out3D['real'] = real['close']
        out3D['predicted'] = predicted['close']
        out3D['predictedABS'] = predicted['close'].abs()
        out3D['hour'] = i
        out3D = out3D.loc[((out3D['predicted'] >= rfilter) | (out3D['predicted'] <=- rfilter))]
        
        out = out.append(out3D)
        
    import plotly.express as px
    fig = px.scatter_3d(out, x='hour', y='predicted', z='real', size='predictedABS', color='hour', height=1000, width=1000)
    fig.show()

hourly_signals_statistics3D('EURUSD', lag=24, hour=10, hour2=23, rfilter=0.000)

En esta función, para el cálculo de los valores pronosticados y reales se usa la fórmula que ya conocemos. Cada diagrama de dispersión aparte muestra la dependencia de un hecho/pronóstico para cada hora, si tomáramos la señal con el incremento de la décima hora del día anterior. Como ejemplo, hemos tomado todas las horas desde las 10.00 hasta las 23.00. Podemos ver que la correlación con las horas más cercanas es máxima, mientras que se reduce con las lejanas (los diagramas de dispersión se hacen más parecidos al entorno). A partir de la hora 16, las horas del día actual dependen ya poco de la hora 10 del día anterior. En los archivos adjuntos al artículo, usted podrá girar el objeto 3D y destacar los fragmentos que le interesen para obtener información más precisa.

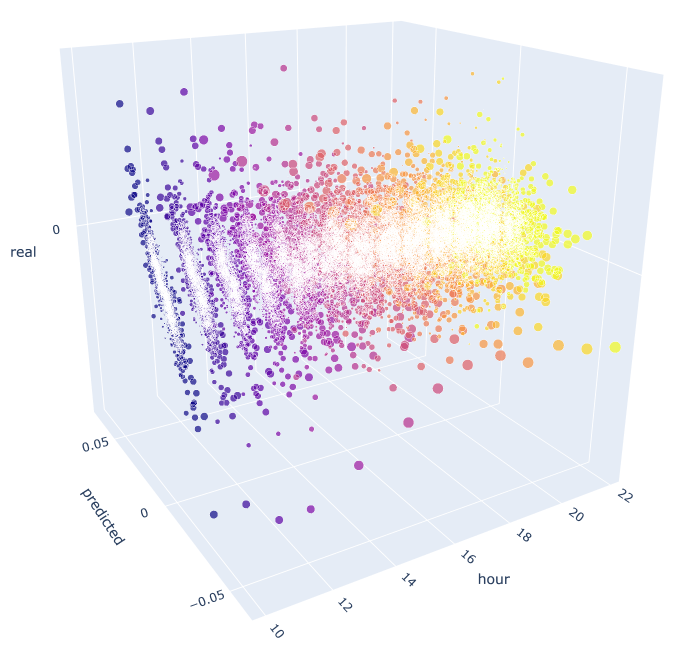
Fig. 10. Diagrama de dispersión en 3D para los incrementos reales y pronosticados en el periodo 2015-2020.

Solo queda escribir el experto y ver cómo funciona.

Ejemplo de experto que comercia con las dependencias estacionales encontradas

Por analogía con el ejemplo del anterior artículo, este robot comerciará con una ley de mercado basada solo en la interrelación estadística de los incrementos actual y anterior de una hora concreta. La única diferencia es que comerciará con otras horas y según otro principio, basado en la fórmula propuesta. 

Proponemos al lector analizar un ejemplo sobre el uso de la fórmula obtenida para el comercio, basada en la investigación estadística realizada:

input int OpenThreshold = 30;     //Open threshold
input int OpenThreshold1 = 30;    //Open threshold 1
input int OpenThreshold2 = 30;    //Open threshold 2
input int OpenThreshold3 = 30;    //Open threshold 3
input int OpenThreshold4 = 30;    //Open threshold 4
input int Lag = 10;
input int stoploss = 150;         //Stop loss
input int OrderMagic = 666;       //Orders magic
input double   MaximumRisk=0.01;  //Maximum risk
input double   CustomLot=0;       //Custom lot

Dado que hemos determinado el intervalo con las regularidades de las horas {10, 11, 12, 13, 14} inclusive, podemos establecer el parámetro "Open threshold" para cada hora por separado. Estos parámetros equivalen al parámetro "rfilter" en la fig. 9. La variable "Lag" contiene el valor del lag para los incrementos (recordemos que, por defecto, hemos unalizado un lag de 25, es decir, casi un día completo para el marco temporal de horas). Podríamos establecer un lag para cada hora por separado, pero lo dejaremos igual en todas, para que el experimento resulte más sencillo. Asimismo, hemos dejado el mismo valor de stop loss para todas las posiciones. Todos estos parámetros se pueden optimizar, cosa que haremos más tarde.

La propia lógica comercial tendrá el aspecto que sigue:

void OnTick() {
//---
   if(!isNewBar()) return;
   CopyClose(NULL, 0, 0, Lag*2+1, prArr);
   ArraySetAsSeries(prArr, true);
   const double pr = (prArr[1] - prArr[Lag]) - ((prArr[Lag] - prArr[Lag*2]) - (prArr[Lag-1] - prArr[Lag*2-1]));

   TimeToStruct(TimeCurrent(), hours);

   if(hours.hour >=10 && hours.hour <=14) {

      //if(countOrders(0)==0)
      //   if(pr >= signal && CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_BUY))
      //      OrderSend(Symbol(),OP_BUY,LotsOptimized(), Ask,0,Bid-stoploss*_Point,NormalizeDouble(Ask + signal, _Digits),NULL,OrderMagic,INT_MIN);

      if(CheckMoneyForTrade(_Symbol,LotsOptimized(),ORDER_TYPE_SELL)) {
         if(pr <= -signal && hours.hour==10)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal, _Digits),NULL,OrderMagic);
         if(pr <= -signal1 && hours.hour==11)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal1, _Digits),NULL,OrderMagic);
         if(pr <= -signal2 && hours.hour==12)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal2, _Digits),NULL,OrderMagic);
         if(pr <= -signal3 && hours.hour==13)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal3, _Digits),NULL,OrderMagic);
         if(pr <= -signal4 && hours.hour==14)
            OrderSend(Symbol(),OP_SELL,LotsOptimized(), Bid,0,Ask+stoploss*_Point,NormalizeDouble(Bid - signal4, _Digits),NULL,OrderMagic);
      }
   }
}

La constante "pr" se calcula según la fórmula indicada más arriba. Esta fórmula pronostica el incremento del precio en la barra siguiente. A continuación, comprobamos la condición para cada barra, y si el incremento cumple con el umbral mínimo para una hora concreta, se abrirá una transacción de compra. Recordemos que el desplazamiento de la media de los incrementos hacia la zona negativa vuelve ineficaces las compras en el intervalo de 2015 a 2020. El lector podrá comprobarlo por sí mismo.

Iniciamos la optimización genética con los parámetros indicados en la fig. 11 y nos fijamos en los resultados:

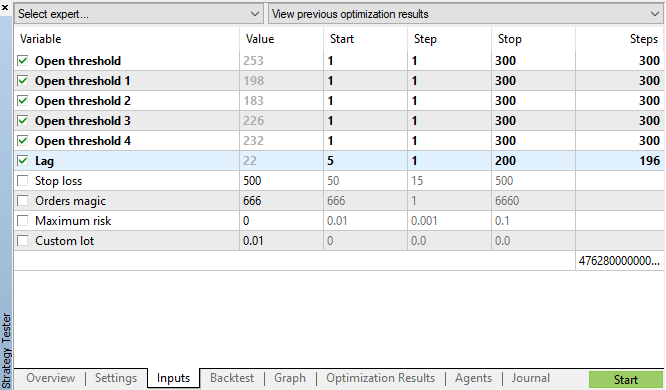
Fig. 11. Recuadro con los parámetros de la optimización genética

Echemos un vistazo al gráfico de optimización. En el intervalo optimizado, los valores de "Lag" más efectivos se ubican en el intervalo de las horas 17-30, lo cual se acerca bastante a nuestra suposición de que los incrementos de una hora concreta del día presente muestran dependencia respecto a la misma hora del día anterior:

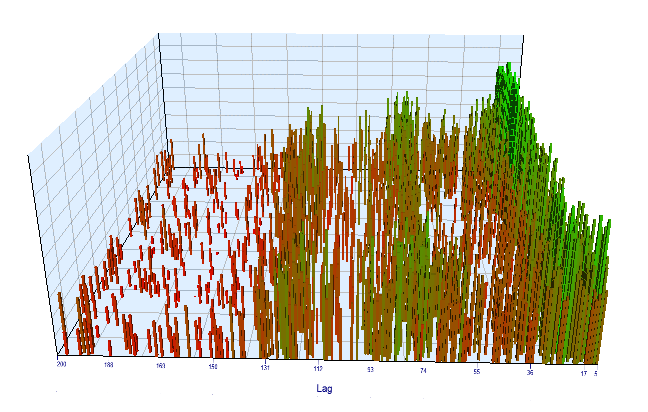
Fig 12. Relación de la variable "Lag" respecto a la variable "Order threshold" en el intervalo optimizado

En el gráfico en tiempo real, tendrá un aspecto similar:

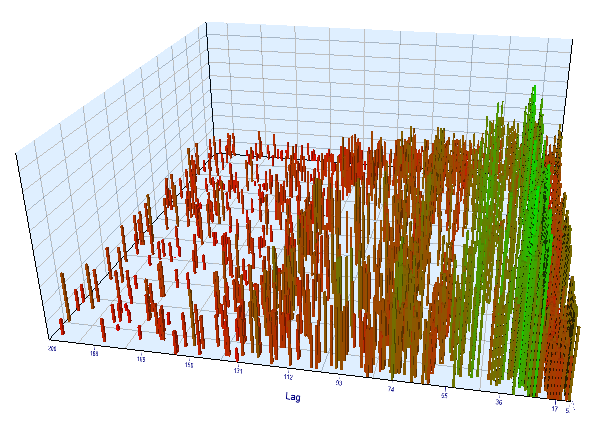
Fig 13. Relación de la variable "Lag" respecto a la variable "Order threshold" en el intervalo en tiempo real

Vamos a analizar con mayor detalle los resultados de los recuadros de optimización de los backtests y los forward tests:

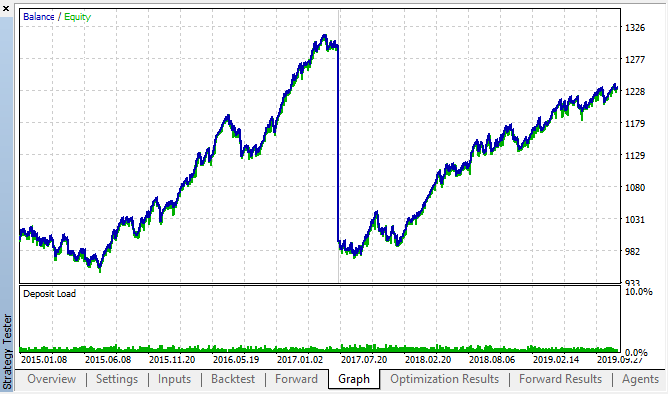
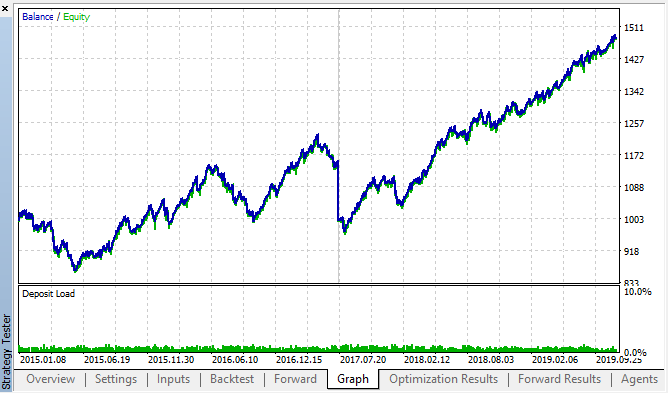
Figs. 14, 15. Gráficos del backtest y las optimizaciones en tiempo real.

Vemos que la regularidad se mantiene en todo el intervalo 2015-2020. Podemos considerar que nuestro enfoque econométrico ha funcionado fabulosamente. Hemos visto que existen dependencias entre los incrementos de las mismas horas para los días de la semana más próximos, con cierta clusterización (la dependencia puede darse, no con la misma hora, pero sí con una próxima). El lector verá cómo usar la segunda ley o regularidad en el siguiente artículo.

Comprobando el periodo de incrementos en otro marco temporal

Vamos a realizar una comprobación adicional en el marco temporal М15. Supongamos que buscamos esa misma interrelación entre la hora actual y la misma hora del día anterior. En este caso, un lag efectivo debe ser 4 veces superior, suponiendo, aproximadamente, 24*4 = 96, dado que en cada hora hay 4 segmentos de 15 minutos. Hemos optimizado el asesor con los mismos ajustes, cambiando el marco temporal a М15.

En el segmento optimizado, el lag de incremento efectivo ha sido <60, lo cual resulta extraño. Quizá el optimizador haya captado otra regularidad, o se haya producido una sobreoptimización.

 

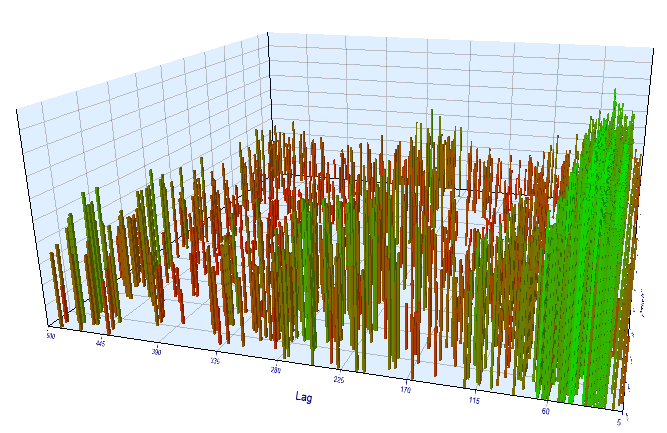
Fig 16. Relación de la variable "Lag" respecto a la variable "Order threshold" en el intervalo optimizado

Vamos a ver los resultados en el test en tiempo real. Resulta curioso que todo esté en orden: el lag efectivo es aproximadamente de 100, lo cual corrobora la regularidad. 

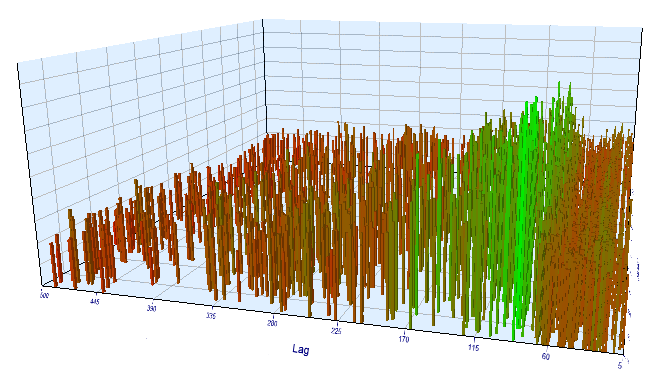
Fig 17. Relación de la variable "Lag" respecto a la variable "Order threshold" en el intervalo en tiempo real

Veamos los mejores resultados de back\forward:

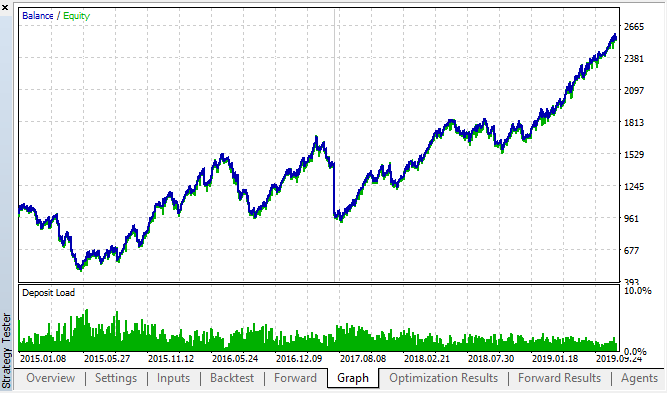
Fig 18. back test y forward, mejor pasada forward

La curva ha resultado similar a la curva del gráfico H1, con un aumento significativo en el número de transacciones. Podemos suponer que esta estrategia también se puede optimizar para marcos temporales más "pequeños".

Conclusión

En el presente artículo, hemos propuesto la siguiente hipótesis:

La correlación de los incrementos se basa en la presencia de ciertas regularidades y leyes estacionales, así como en el agrupamiento (clusterización) de los incrementos que se encuentran próximos. 

Hemos corroborado por completo la primera parte, para ser más concretos: existen dependencias entre incrementos de hora tomados en diferentes días de la semana. Asimismo, hemos corroborado de forma implícita la segunda afirmación: la dependencia muestra una clusterización, y los valores de los incrementos de las horas actuales dependen además de los valores de los incrementos de las horas colindantes.

Merece la pena destacar que el asesor propuesto no es en ningún caso la única variante posible de comercio según las dependencias encontradas. La lógica propuesta refleja el punto de vista del autor sobre las dependencias: la optimización del asesor se ha realizado solo como confimación adicional de las regularidades encontradas a través de la investigación estadística.

Dado que la segunda parte de la prueba requiere de significativas investigaciones adicionales, en el próximo artículo aplicaremos un modelo sencillo de aprendizaje de máquinas para confirmar definitivamente (o bien refutar) la segunda parte de la hipótesis. 

En los anexos, el lector podrá encontrar un entorno de trabajo listo para usar en el formato Jupyter notebook, destinado a la investigación individual de otros instrumentos financieros. Los resultados de las investigaciones se podrá comprobar nuevamente con el asesor de prueba propuesto.