
Mit Boxplot saisonale Muster von Finanzzeitreihen erforschen
Versuchen Sie, die Hypothese der Markteffizienz zu widerlegen und die Existenz von Marktzyklen zu beweisen.
2013 entwickelte Eugene Fama die Markteffizienzhypothese und gewann den Nobelpreis für Wirtschaftswissenschaften. Seiner Hypothese zufolge spiegeln die Vermögenspreise alle wesentlichen Informationen vollständig wider. Dies bedeutet, dass keiner der Marktteilnehmer Vorteile gegenüber anderen hat.
Die Hypothese selbst hat jedoch einige Vorbehalte, während die Effizienz die folgenden drei Grade haben kann:
- schwach, wenn der Marktpreis der Vermögenswerte die Informationen der Vergangenheit vollständig widerspiegelt
- durchschnittlich, wenn der Preis nicht nur die Vergangenheit, sondern auch die aktuelle öffentliche Information widerspiegelt
- stark, wenn sie zusätzlich nicht-öffentliche Insider-Informationen widerspiegelt
Je nach Effizienzgrad haben die Märkte einen unterschiedlichen Grad an Vorhersehbarkeit. Für einen technischen Analysten bedeutet dies, dass es verschiedene zyklische, saisonale Komponenten im Markt geben kann.
So kann die Marktaktivität beispielsweise von Jahr zu Jahr, von Monat zu Monat, von Sitzung zu Sitzung, von Stunde zu Stunde usw. variieren. Darüber hinaus können diese Zyklen einige vorhersehbare Sequenzen darstellen, innerhalb und zwischen denen der Trader sein Alpha finden kann. Die Zyklen können sich auch überlappen und unterschiedliche Kompositionsmuster erzeugen, die weiter untersucht werden können.
Suche nach saisonalen Mustern in Preisschritten
Wir können regelmäßige Zyklen zusammen mit zusammengesetzten Zyklen studieren. Betrachten wir das Beispiel der Untersuchung der monatlichen Schwankungen eines Finanzinstruments. Zu diesem Zweck werden wir die Kombination der IPython-Sprache und des MetaTrader 5-Terminals verwenden.
Um den Import von Kursen direkt vom Terminal zu erleichtern, werden wir den folgenden Code verwenden:
from MetaTrader5 import * from datetime import datetime import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import seaborn; seaborn.set() # Initializing MT5 connection MT5Initialize("C:\\Program Files\\MetaTrader 5\\terminal64.exe") MT5WaitForTerminal() print(MT5TerminalInfo()) print(MT5Version())
Geben Sie den Pfad Ihres Terminals an, der sich von meinem unterscheiden kann.
Fügen Sie ein paar weitere Zeilen hinzu, um die Analyse zu starten:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_D1, datetime(2010, 1, 1), datetime(2020, 1, 1)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
returns.head(5)
Monthly_Returns = returns.groupby([returns.index.year.rename('year'), returns.index.month.rename('month')]).mean()
Monthly_Returns.boxplot(column='close', by='month', figsize=(15, 8))
Die Variable rates erhält den Pandas-Datenrahmen mit Preisen über das angegebene Zeitintervall (in diesem Beispiel z.B. 10 Jahre). Angenommen, wir sind nur an engen Preisen interessiert (um die weitere Interpretation zu vereinfachen). Lassen Sie uns die unnötigen Datenspalten mit der Methode rates.drop() löschen.
Die Preise haben eine Verschiebung des Mittelwertes im Laufe der Zeit und bilden Trends, daher ist die statistische Analyse nicht auf solche Rohreihen anwendbar. In der Ökonometrie werden in der Regel prozentuale Preisänderungen (Preiserhöhungen) verwendet, um sicherzustellen, dass sie alle im gleichen Wertebereich liegen. Die prozentualen Änderungen können mit der Methode pd.DataFrame(rates['close'].pct_change(1)) abgefragt werden.
Wir benötigen durchschnittliche monatliche Preisbereiche. Ordnen wir die Tabelle so an, dass wir die Mittelwerte der monatlichen Zuwächse nach Jahren erhalten und sie im Boxplot-Diagramm anzeigen können.
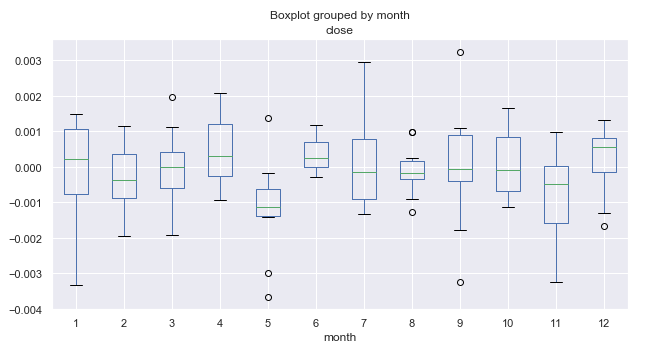
Abb. 1. Die durchschnittliche Preissteigerung erstreckt sich über 10 Jahre auf einen Monat.
Was sind Boxplots und wie sind sie zu interpretieren?
Wir müssen auf Daten über die Volatilität oder die Verteilung von Preisdaten für einen ausgewählten Zeitraum zugreifen. Jedes separate Boxplot (oder Box-and-Whiskey-Diagramm) bietet eine gute Visualisierung der Verteilung von Werten entlang des Datensatzes. Boxplots sollten nicht mit den Kerzencharts verwechselt werden, obwohl sie visuell ähnlich aussehen. Im Gegensatz zu Kerzenständern bieten Boxplots eine standardisierte Möglichkeit, die Verteilung der Daten auf der Grundlage von fünf Messwerten anzuzeigen.
- Median, Q2 oder das 50. Perzentil zeigt den Durchschnittswert des Datensatzes an. Der Wert erscheint als grüne horizontale Linien innerhalb der Kästchen im Diagramm.
- Das erste Quartil, Q1 (oder das 25. Perzentil) stellt den Median zwischen Q2 und dem kleinsten Wert innerhalb der Stichprobe dar, der in das 99%-Konfidenzintervall fällt. Es wird als unterer Rand des „Körpers“ im Diagramm angezeigt.
- Das dritte Quartil, Q3 (oder das 75. Perzentil) ist der Median zwischen Q2 und dem Maximalwert, der als oberer Rand des „Körper“ angezeigt wird.
- Der Körper der Box bildet einen Interquartilsbereich (zwischen dem 25. und dem 75. Perzentil), der auch als IQR bezeichnet wird.
- Die „Haare“ der Boxen ergänzen die Verteilung. Sie decken 99% der gesamten Stichprobenvarianz ab, und die Punkte oberhalb und unterhalb zeigen Werte außerhalb des 99%-Wertebereichs an.
Diese Daten reichen aus, um die Bandbreite der Schwankungen und die Streuung der Werte innerhalb des internen Bereichs zu bewerten.
Weitere Analysen der saisonalen Muster
Betrachten wir Abbildung 1 im Detail. Wir sehen, dass der Median der Inkremente für den fünften Monat (Mai) relativ zu Null nach unten verschoben ist und einen sichtbaren Ausreißer über Null aufweist. Wie wir aus der 10-Jahres-Statistik ersehen können, war der Markt im Mai im Allgemeinen im Vergleich zum März rückläufig. Es gab nur ein Jahr, in dem der Markt im Mai wuchs. Dies ist eine interessante Idee, die gut mit dem Händlersprichwort „Sell in May and go away“ (Verkaufe im Mai und geh weg!) übereinstimmt.
Werfen wir einen Blick auf den 6. Monat (Juni), der dem Mai folgt. Fast immer (mit Ausnahme eines Jahres) wuchs der Markt im Juni im Vergleich zum Mai, was sich als ein Muster erweist, das sich von Jahr zu Jahr wiederholt. Die Schwankungsbreite im Juni ist recht gering, ohne Ausreißer (im Gegensatz zum Mai), was auf eine gute saisonale Stabilität hinweist.
Achten Sie auf den 11. Monat (November). Die Wahrscheinlichkeit, dass der Markt in diesem Zeitraum rückläufig ist, ist hoch. Danach, im Dezember, ist der Markt normalerweise wieder gestiegen. Der Januar (der 1. Monat) war durch eine hohe Volatilität und einen Rückgang im Vergleich zum Dezember gekennzeichnet.
Die gewonnenen Daten können einen nützlichen Überblick über die Rahmenbedingungen für Handelsentscheidungen liefern. Außerdem können Wahrscheinlichkeiten in ein Handelssystem integriert werden. So kann es beispielsweise in bestimmten Monaten mehr Käufe oder Verkäufe durchführen.
Die monatlichen Zyklusdaten sind sehr interessant, aber es ist möglich, noch tiefer in kürzere Tageszyklen zu schauen.
Betrachten wir die Verteilung der Preiserhöhungen für jeden einzelnen Wochentag unter Verwendung desselben Zehnjahreszeitraums:
Daily_Returns = returns.groupby([returns.index.week.rename('week'), returns.index.dayofweek.rename('day')]).mean()
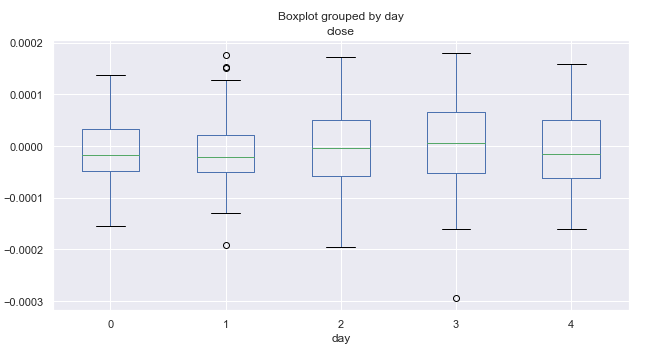
Abb. 2. Die durchschnittliche Preissteigerung reicht nach Handelstagen über 10 Jahre.
Dabei entspricht Null dem Montag und vier dem Freitag. Entsprechend der Preisspanne bleibt die Volatilität nach Tagen nahezu konstant. Es kann nicht gefolgert werden, dass der Handel an einem bestimmten Wochentag intensiver ist. Im Durchschnitt neigt der Markt an Montagen und Freitagen eher zu einem Rückgang als zu einem Anstieg. Vielleicht sieht die Verteilung nach Tagen in einigen Monaten anders aus. Lassen Sie uns eine zusätzliche Analyse durchführen.
# leave only one month "returns.index[~returns.index.month.isin([1])" returns = returns.drop(returns.index[~returns.index.month.isin([1])])
Im obigen Code wird 1 für Januar verwendet. Wenn Sie diesen Wert ändern, können wir Statistiken für jeden Monat erhalten, in unserem Fall für 10 Jahre.
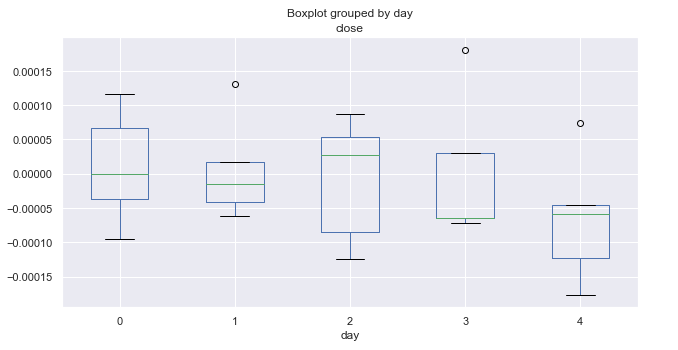
Abb. 3. Durchschnittliche Preissteigerungsraten nach Handelstagen, über 10 Jahre (Januar).
Das obige Diagramm zeigt die Verteilung der Inkremente nach Tagen für Januar. Das Diagramm bietet nun mehr nützliche Details im Vergleich zu den zusammenfassenden Statistiken für alle Monate. Es zeigt deutlich, dass der Markt freitags tendenziell rückläufig ist. Nur einmal ist das EURUSD-Paar nicht gesunken (dargestellt durch einen Ausreißer über Null).
Hier sind ähnliche Statistiken für März:
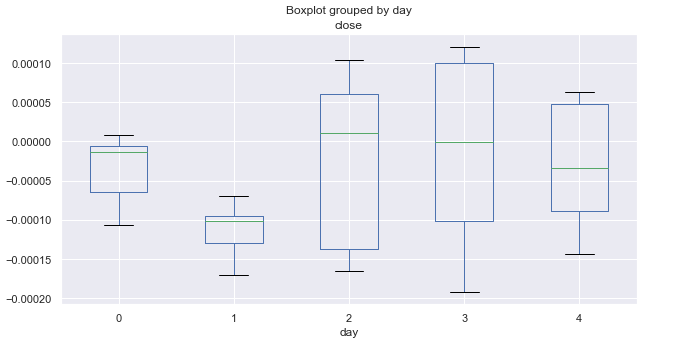
Abb. 4. Durchschnittliche Preissteigerungsraten nach Handelstagen, über 10 Jahre (März).
Die März-Statistik ist völlig anders als die vom Januar. Montag und Dienstag (insbesondere der Dienstag) zeigen einen rückläufigen Trend. Alle Dienstage schlossen mit einem deutlichen Rückgang, während die übrigen Tage (im Durchschnitt) um Null schwanken.
Werfen wir einen Blick auf den Oktober:
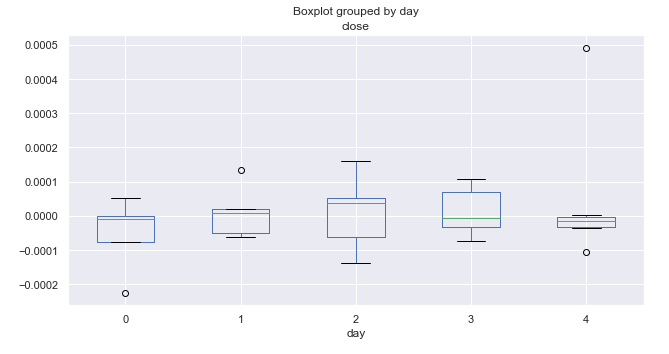
Abb. 5. Durchschnittliche Preissteigerungsraten nach Handelstagen, über 10 Jahre (Oktober).
Die Analyse der Verteilung der Preissteigerung nach Wochentagen ergab keine auffälligen Muster. Wir können nur den Mittwoch ausmachen, der die größte Bandbreite und das größte Potenzial für Preisbewegungen aufweist. Alle anderen Tage zeigen die gleiche Wahrscheinlichkeit für Aufwärts- und Abwärtsbewegungen und weisen einige Ausreißer auf.
Analyse der saisonalen Intraday-Muster
Sehr oft ist es notwendig, bei der Erstellung eines Handelssystems die Intraday-Verteilungen zu berücksichtigen, z.B. um zusätzlich zu den Tages- und Monatsverteilungen auch stündliche Daten zu verwenden. Dies ist leicht möglich.
Berücksichtigen Sie die Verteilung der Preisschritte für jede Stunde:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
# get percent change (price returns)
returns = pd.DataFrame(rates['close'].pct_change(1))
returns = returns.set_index(rates['time'])
returns = returns[1:]
Hourly_Returns = returns.groupby([returns.index.day.rename('day'), returns.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(10, 5))
Dies sind die Kurse des 15-minütigen Zeitrahmens für 10 Jahre. Ein weiterer Unterschied besteht darin, dass die Daten nach Tagen und Stunden gruppiert werden, um den Median der stündlichen Statistik für alle Tage der Unterstichprobe zu erhalten.
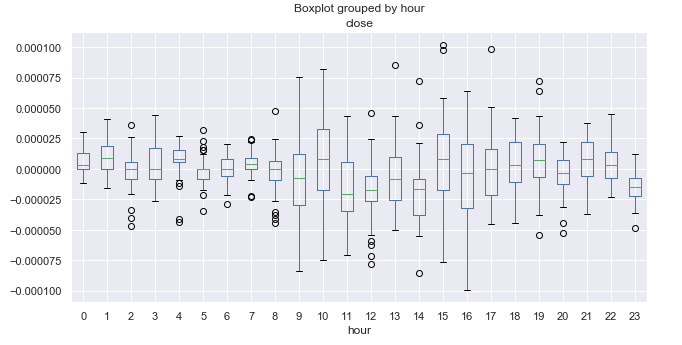
Abb. 6. Durchschnittliche Preissteigerungsraten nach Stunden, über 10 Jahre.
Hier ist es notwendig, die Zeitzone des Terminals zu kennen. In meinem Fall ist es + 2. Als Referenz schreiben wir die Öffnungs- und Schließzeiten der wichtigsten FOREX-Handelssitzungen in UTC+2.
| Handelssitzung | Eröffnung | Schließzeit |
|---|---|---|
| Pazifik | 21.00 | 08.00 |
| Asien | 01.00 | 11.00 |
| Europa | 08.00 | 18.00 |
| Amerika | 14.00 | 00.00 |
Der Handel während der Pazifik-Sitzung ist normalerweise ruhig. Wenn Sie sich die Größe der Boxen ansehen, können Sie leicht feststellen, dass die Spanne zwischen 21.00-08.00 Uhr minimal ist, was einem ruhigen Handel entspricht. Die Spanne nimmt nach der Eröffnung der europäischen und amerikanischen Sitzung zu und beginnt dann allmählich zu kleiner zu werden. Es scheint keine offensichtlichen zyklischen Muster zu geben, die im täglichen Zeitrahmen deutlich waren. Der durchschnittliche Zuwachs schwankt um Null, ohne dass es klare Aufwärts- oder Abwärtsstunden gibt.
Eine interessante Periode ist 23.00 Uhr (Schließzeit der amerikanischen Sitzung), während der die Preise normalerweise im Vergleich zu 22.00 Uhr sinken. Dies kann ein Hinweis auf eine Korrektur am Ende der Börsensitzung sein. Um 00.00 Uhr wachsen die Preise relativ zu 23.00 Uhr, so dass dies als Regelmäßigkeit behandelt werden kann. Es ist schwierig, ausgeprägtere Zyklen zu erkennen, aber wir haben ein vollständiges Bild der Preisspanne und wissen, was zu diesem Zeitpunkt zu erwarten ist.
Eine Abweichung in Schritten mit einer einzigen Verzögerung kann einige Muster verdecken. Es wäre also vernünftig, Daten zu betrachten, die durch einen gleitenden Durchschnitt mit einer willkürlichen Periode beeinträchtigt werden.
Suchen Sie nach saisonalen Mustern, die durch einen MA bereinigt sind.
Die richtige Bestimmung der Trendkomponente ist sehr schwierig. Manchmal werden die Zeitreihe zu stark geglättet. In diesem Fall gibt es nur wenige Handelssignale. Wenn die Glättungsperiode verkürzt wird, kann die hohe Häufigkeit der Geschäfte den Spread und die Provision nicht abdecken. Lassen Sie uns den Code so bearbeiten, dass der Abschlag mit Hilfe eines gleitenden Durchschnitts erfolgt:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2010, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
# leave only 'time' and 'close' columns
rates = rates.drop(['open', 'low', 'high', 'tick_volume', 'spread', 'real_volume'], axis=1)
rates = rates.set_index('time')
# set the moving average period
window = 25
# detrend tome series by MA
ratesM = rates.rolling(window).mean()
ratesD = rates[window:] - ratesM[window:]
plt.figure(figsize=(10, 5))
plt.plot(rates)
plt.plot(ratesM)
Der Glättungslänge des gleitenden Durchschnitts wird auf 25 festgelegt. Dieser Parameter kann ebenso wie die Periodenlänge, für die Schlusskurse angefordert werden, geändert werden. Ich verwende den 15-Minuten-Zeitrahmen. Als Ergebnis erhalten wir für jede Stunde die durchschnittliche Abweichung der Schlusskurse vom gleitenden 15-Minuten-Durchschnitt. Hier ist die resultierende Zeitreihe:
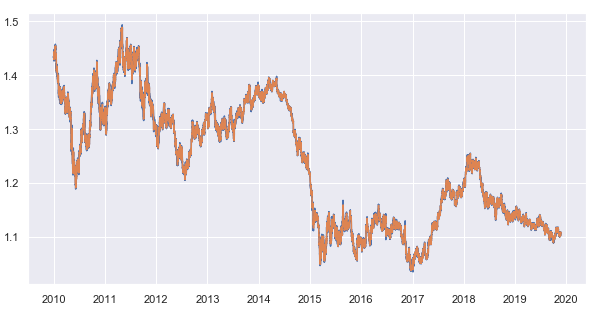
Abb. 7. 15-Minuten-Schlusskurse und der gleitende Durchschnitt mit der Glättungslänge von 25
Subtrahieren Sie den gleitenden Durchschnitt von den Schlusskursen und erhalten Sie eine trendbereinigten Zeitreihe (Differenz):
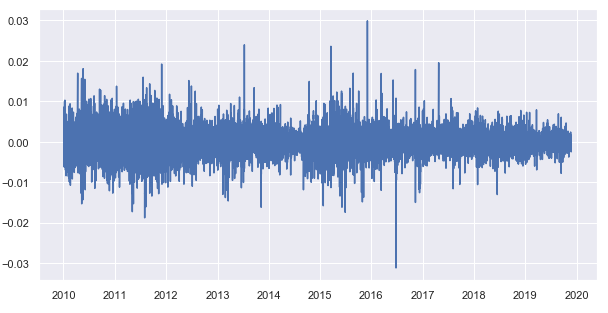
Abb. 8. Differenzen aus der Subtraktion des gleitenden Durchschnitts von den Schlusskursen
Nun lassen Sie uns die stündliche Statistik der Verteilung der Differenzen für jede Handelsstunde abrufen:
Hourly_Returns = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).median()
Hourly_Returns.boxplot(column='close', by='hour', figsize=(15, 8))
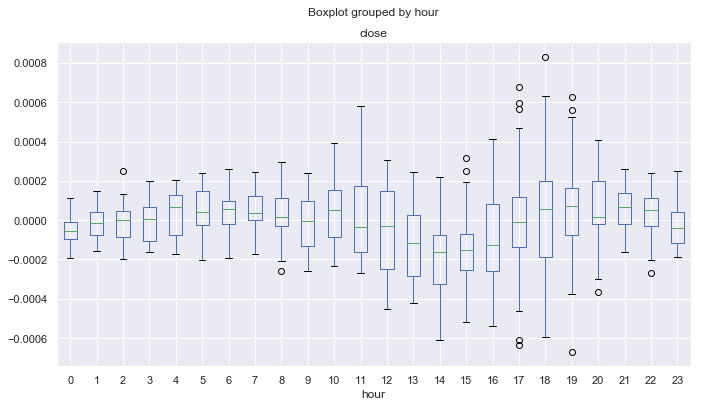
Abb. 9. Die durchschnittlichen Preisänderungen in über 10 Jahre nach Stunden, bereinigt durch den 25er MA.
Im Gegensatz zu dem Diagramm in Abbildung 6, das für Preiserhöhungen mit einer einzigen Verzögerung erstellt wurde, zeigt dieses Diagramm weniger Ausreißer und zeigt mehr zyklische Muster. Beispielsweise können Sie sehen, dass die Preise von 0,00 bis 08,00 (Pazifik-Session) normalerweise relativ zum gleitenden Durchschnitt gleichmäßig steigen. Ein Abwärtstrend kann von 12.00 bis 14.00 Uhr definiert werden. Danach, während der US-Sitzung, steigen die Preise im Durchschnitt. Nach dem Beginn der Pazifik-Sitzung sinken die Preise für 4 Stunden, beginnend ab 21.00 Uhr.
Der nächste logische Schritt besteht darin, die Verteilungsmomente zu untersuchen, um genauere statistische Schätzungen zu erhalten. Berechnen Sie zum Beispiel die Standardabweichung für die resultierende, trendbereinigte Reihe als Boxplot-Diagramm:
Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).std()
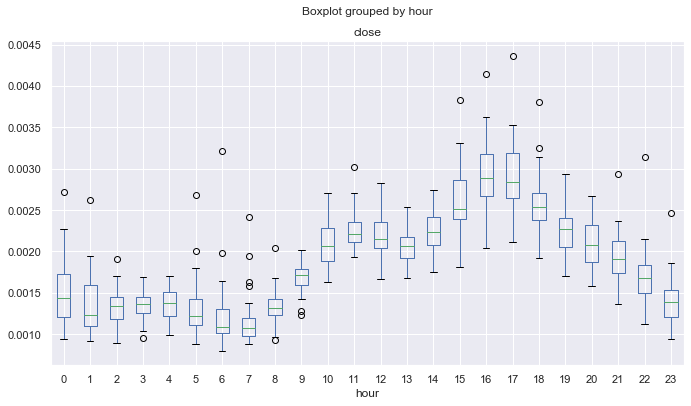
Abb. 10. Durchschnittliche Standardabweichungen der Preiserhöhungen nach Stunden, über 10 Jahre, bereinigt durch dern 25er MA.
Abb. 10 zeigt die Stunden mit dem stabilsten Preisverhalten in Bezug auf die Standardabweichung von den mathematischen Erwartungen. Zum Beispiel haben die Stunden 4, 13, 14, 19 eine stabile Streuung an allen Tagen und können für Strategien der mittleren Reversion attraktiv sein. Andere Stunden können Ausreißer und einen langen „Schnurrbart“ aufweisen, was auf eine variablere Volatilität an verschiedenen Tagen hinweist.
Ein weiterer interessanter Punkt ist der Asymmetriekoeffizient. Berechnen wir ihn:
Hourly_skew = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).skew()

Abb. 11. Durchschnittliche Asymmetriekoeffizienten der Preiserhöhungen nach Stunden, über 10 Jahre, bereinigt den 25er MA.
Die Nähe zu Null und eine geringe Streuung weisen auf eine eher „normale“ Verteilung der Inkremente hin. Die Diagrammform wird hier konkav. Obwohl beispielsweise die Fluktuationen in der europäischen und amerikanischen Sitzung eine größere Streuung aufweisen (Abb. 9), sind ihre stündlichen Verteilungen stabiler und weniger verzerrt, im Gegensatz zu den pazifischen und asiatischen Sitzungen. Dies kann auf große Fluktuationen der Aktivität während der letzten beiden Sitzungen zurückzuführen sein, wenn fast keine Handelsaktivität durch plötzliche Bewegungen ersetzt wird, die viel zur Verzerrung der Verteilung beitragen.
Die Überstandsstatistiken zeigen ähnliche Ergebnisse:
Hourly_std = ratesD.groupby([ratesD.index.day.rename('day'), ratesD.index.hour.rename('hour')]).apply(pd.DataFrame.kurt)
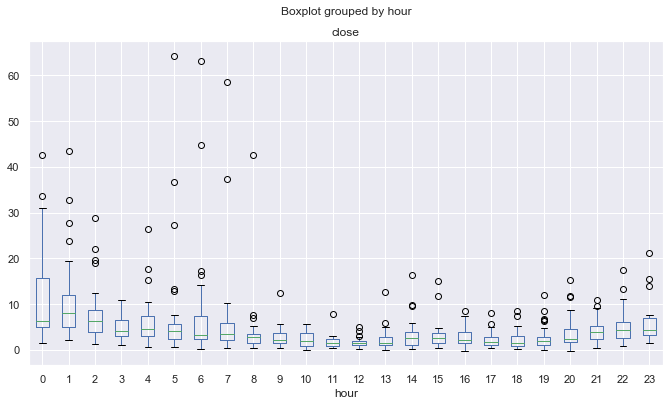
Abb. 12. Die durchschnittlichen Überstände der Preiserhöhungen nach Stunden, über 10 Jahre, bereinigt durch den 25er MA.
Aufgrund des oben erwähnten möglichen Effekts weisen die Verteilungen weniger Spitzen auf und sind "gleichförmiger" in volatileren Handelssitzungen, während sie "weniger gleichförmig" in ruhigen Handelssitzungen sind. Dies ist eine Art Paradoxon.
Suchen Sie nach saisonalen Mustern, die durch einen MA bereinigt sind, für einen bestimmten Monat oder Wochentag.
Wir können die detaillierte Verteilung der Stundenpreise für jeden Monat und für jeden Wochentag separat einsehen. Der gesamte Code ist in den Anhängen unten verfügbar. Hier werde ich nur den Vergleich zwischen März und November besprechen.
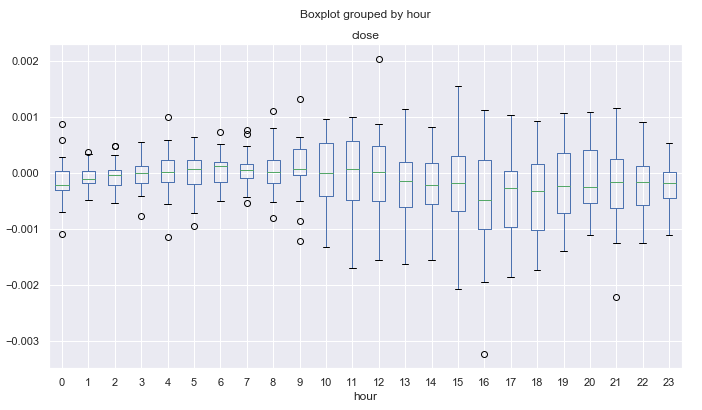
Abb. 13. Die durchschnittlichen Preisänderungen in über 10 Jahre nach Stunden, bereinigt durch den 25er MA, für März.
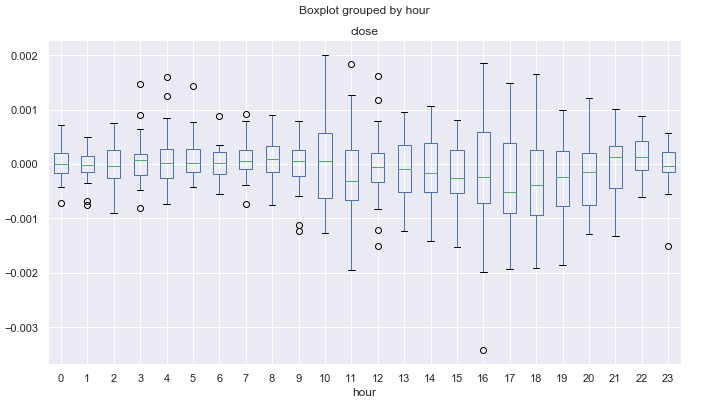
Abb. 14. Die durchschnittlichen Preisänderungen in über 10 Jahre nach Stunden, bereinigt durch den 25er MA, für November.
Es ist möglich, nach noch kleineren Intraday-Zyklen zu suchen, auch nach Tickdaten, aber hier geht es nur um die grundlegenden saisonalen Muster, die nach Meinung der Händler in Finanzzeitreihen vorkommen können. Sie können diese Daten für die Entwicklung Ihrer eigenen Handelssysteme verwenden und dabei die saisonalen Merkmale des Finanzinstruments berücksichtigen.
Überprüfung der Muster mit Hilfe der Handelslogik
Lassen Sie uns einen einfachen, handelnden Expert Advisor erstellen, der die in Abb. 9 gezeigten gefundenen Muster verwendet. Es zeigt, dass die EURUSD-Kurse von 0,00 bis 04,00 (GMT+2) während der vier Stunden relativ zu ihrem Durchschnitt steigen.
//+------------------------------------------------------------------+ //| Seasonal trader.mq5 | //| Copyright 2020, Max Dmitrievsky | //| https://www.mql5.com/en/users/dmitrievsky | //+------------------------------------------------------------------+ #property copyright "Copyright 2020, Max Dmitrievsky" #property link "https://www.mql5.com/en/users/dmitrievsky" #property version "1.00" #include <MT4Orders.mqh> #include <Trade\AccountInfo.mqh> #include <Math\Stat\Math.mqh> input int OrderMagic = 666; input double MaximumRisk=0.01; input double CustomLot=0; int hnd = iMA(NULL, 0, 25, 0, MODE_SMA, PRICE_CLOSE); MqlDateTime hours; double maArr[], prArr[]; void OnTick() { //--- CopyBuffer(hnd, 0, 0, 1, maArr); CopyClose(NULL, 0, 0, 1, prArr); double pr = prArr[0] - maArr[0]; TimeToStruct(TimeCurrent(), hours); if(hours.hour >=0 && hours.hour <=4) if(countOrders(0)==0 && countOrders(1)==0) if(pr < -0.0002) OrderSend(Symbol(),OP_BUY,0.01,SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN); if(countOrders(0)!=0 && pr >=0) for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) { if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; } } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int countOrders(int a) { int result=0; for(int k=0; k<OrdersTotal(); k++) { if(OrderSelect(k,SELECT_BY_POS,MODE_TRADES)==true) if(OrderType()==a && OrderMagicNumber()==OrderMagic && OrderSymbol() == _Symbol) result++; } return(result); }
Der verwendete gleitende Durchschnitt ist derselbe wie für die statistische Schätzung. Er hat eine Glättungslänge von 25. Subtrahieren Sie den Durchschnittswert vom letzten bekannten Preis und prüfen Sie, ob die aktuelle Handelszeit im Bereich von 0:00 bis einschließlich 4:00 liegt. Wie aus dem Diagramm in Abb. 9 ersichtlich ist, beträgt die maximale Differenz zwischen dem Schlusskurs und dem gleitenden Durchschnitt über diesen Zeitraum -0,0002, während der MA über Null liegt. Dementsprechend besteht unsere Handelslogik darin, zu kaufen, wenn diese Differenz erreicht ist, und die Position zu schließen, wenn sie auf Null kollabiert. Der Testroboter hat keine Stop-Orders oder andere Prüfungen und ist nur zum Testen der gefundenen Muster gedacht. Führen Sie von 2015 bis 2019 einen Test mit dem 15-Minuten-Zeitrahmen durch (der MA wurde in unserer Studie ebenfalls auf diesem Zeitraum aufgebaut), und zwar im Modus „Jeder Tick“:
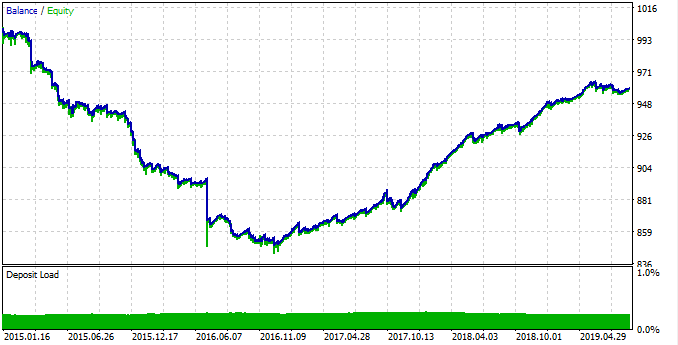
Abb. 15. Testen des gefundenen Musters.
Das Muster funktionierte von 2015 bis 2017 schlecht, und der Saldo war rückläufig. Dann wird ein stabiles Wachstum von 2017 bis 2019 gezeigt. Warum ist dies geschehen? Um es zu verstehen, betrachten wir die Statistiken für jedes Zeitintervall separat.
Zuerst ist hier das profitable Handelsintervall:
rates = pd.DataFrame(MT5CopyRatesRange("EURUSD", MT5_TIMEFRAME_M15, datetime(2017, 1, 1), datetime(2019, 11, 25)),
columns=['time', 'open', 'low', 'high', 'close', 'tick_volume', 'spread', 'real_volume'])
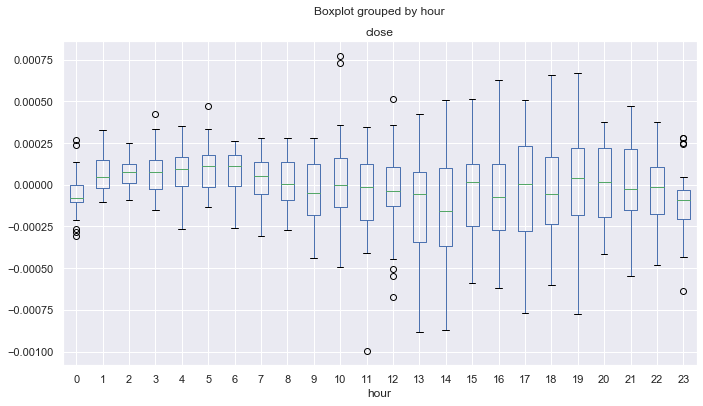
Abb. 16. Statistik der Jahre 2017-2019.
Wie man sieht, liegen die Mediane für alle Stunden (außer Null) über Null, relativ zum gleitenden Durchschnitt. Statistisch gesehen ist Alpha auf der Seite unseres Handelssystems und das System bleibt im Durchschnitt im Gewinn. Nun, hier ist die Verteilung für 2015-2017.
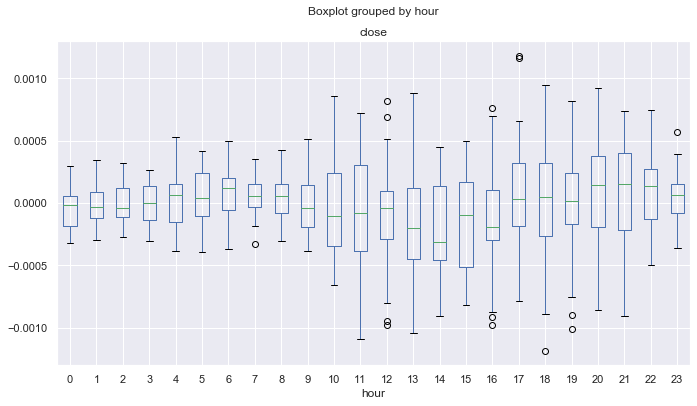
Abb. 17. Statistik der Jahre 2015-2017.
Hier liegt der Median der Verteilung für alle Stunden außer der vierten Stunde unter oder gleich Null, was eine geringere Wahrscheinlichkeit bedeutet, einen Gewinn zu erzielen. Darüber hinaus haben die Boxen eine deutlich größere durchschnittliche Spannweite im Vergleich zu einem anderen Zeitintervall, für das der Mindestwert nicht unter -0,00025 liegt. Hier liegt er bei fast -0,0005. Ein weiterer Nachteil ist die Schätzung von Verteilungen nur bei knappen Preisen, so dass Preisspitzen nicht berücksichtigt werden. Dies kann durch die Analyse der Tick-Daten behoben werden, was den Rahmen dieses Artikels sprengt. Der Unterschied ist klar, und so können Sie versuchen, das System so zu verfeinern, dass die Ergebnisse für alle Jahre ausgeglichen werden.
Erlauben wir die Öffnung von Positionen nur um die Stunden 0-1. Wir gehen also davon aus, dass die Position in den nächsten Stunden mit Gewinn abgeschlossen wird, denn die mittlere Abweichung bewegt sich tendenziell in eine positive Richtung. Erhöhen Sie auch die Schwelle für den Geschäftsabschluss von 0,0 auf 0,0003, und so kann der Roboter mehr potenziellen Gewinn mitnehmen. Die Änderungen sind im folgenden Code dargestellt:
TimeToStruct(TimeCurrent(), hours); if(hours.hour >=0 && hours.hour <=1) if(countOrders(0)==0 && countOrders(1)==0) if(pr < -0.0004) OrderSend(Symbol(),OP_BUY,LotsOptimized(), SymbolInfoDouble(_Symbol,SYMBOL_ASK),0,0,0,NULL,OrderMagic,INT_MIN); if(countOrders(0)!=0 && pr >= 0.0003) for(int b=OrdersTotal()-1; b>=0; b--) if(OrderSelect(b,SELECT_BY_POS)==true && OrderMagicNumber() == OrderMagic) { if(OrderClose(OrderTicket(),OrderLots(),OrderClosePrice(),0,Red)) {}; }
Testen wir den Roboter, um die abschließende Schlussfolgerungen zu ziehen:
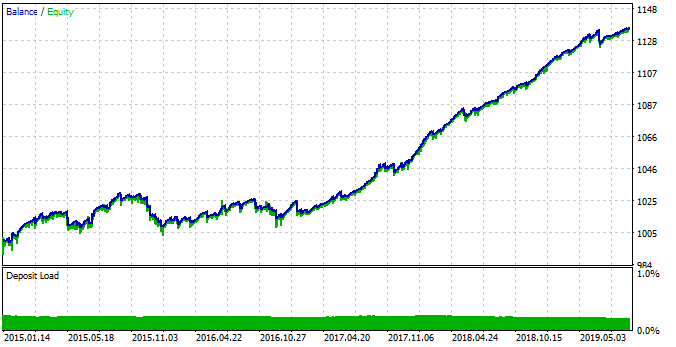
Abb. 18. Testen des erkannten Musters mit geänderten EA-Parametern.
Diesmal ist das System im Zeitintervall zwischen 2015 und 2017 stabiler. Allerdings war dieser Zeitraum aufgrund der veränderten saisonalen Muster nicht so effizient wie der Zeitraum zwischen 2017 und 2019. Dieses Verhalten hängt mit grundlegenden Veränderungen im Markt zusammen, die sich mit Hilfe von Boxplot-Diagrammen leicht beschreiben lassen.
Natürlich gibt es noch viele unerforschte Muster, aber dieses grundlegende Beispiel gibt ein Verständnis für neue interessante Möglichkeiten, die sich bei der Anwendung einer solchen Technik eröffnen.
Schlussfolgerung
Dieser Artikel enthält eine Beschreibung der vorgeschlagenen statistischen Methode zur Erkennung von Saisonmustern in finanziellen Zeitreihen. Der Markt kann sowohl monatliche Saisonzyklen als auch Intraday-Zyklen je nach Monat aufweisen. Die stündliche Analyse hat gezeigt, dass man mit einer bestimmten Glättungsperiode (z.B. einem gleitenden Durchschnitt) bestimmte Zyklen sowohl innerhalb der Sitzungen als auch beim Übergang von einer Handelssitzung zur anderen finden kann.
Einer der Vorteile dieses Ansatzes ist die Möglichkeit, mit spezifischen Marktmustern zu arbeiten und das Fehlen von Überoptimierung (Parameterüberanpassung), wodurch das Handelssystem sehr stabil sein kann.
Was die Nachteile betrifft, so ist der Prozess des saisonalen Musterabbaus nicht einfach und beinhaltet Operationen mit verschiedenen Kombinationen und Zyklen.
Die Analyse wurde für das Währungspaar EURUSD mit dem Zeitintervall von 10 Jahren durchgeführt. Die Python-Quellcodes sind am Ende des Artikels im .ipynb-Format (Jupyter-Notebook) angehängt. Sie können die gleiche Studie für jedes gewünschte Finanzinstrument mit Hilfe der beigefügten Bibliothek durchführen und die erhaltenen Ergebnisse zur Erstellung Ihres eigenen Handelssystems oder zur Verbesserung eines bestehenden Systems anwenden.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/7038
 Die Funktionen des Strategy Builders erweitern
Die Funktionen des Strategy Builders erweitern
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.