По теме "Основы регрессионного анализа" имеется следующие ссылки.
Davidson, Russell and James G. MacKinnon (1993). Estimation and Inference in Econometrics, Oxford: Oxford University Press.
Greene, William H. (2008). Econometric Analysis, 6th Edition, Upper Saddle River, NJ: Prentice-Hall.
Johnston, Jack and John Enrico DiNardo (1997). Econometric Methods, 4th Edition, New York: McGraw-Hill.
Pindyck, Robert S. and Daniel L. Rubinfeld (1998). Econometric Models and Economic Forecasts, 4th edition, New York: McGraw-Hill.
Wooldridge, Jeffrey M. (2000). Introductory Econometrics: A Modern Approach. Cincinnati, OH: South-Western College Publishing.
Приведу пример регрессии., которая ничто иное как функция (зависимая переменная) зависящая от своих аргументов (независимые переменные, регрессоры). При вычислении регрессии необходимо выполнить несколько шагов:
1. Необходимо записать уравнение.
Возьму горячо любимую МА, но взвешенную, так для меня прощу, вычисляя ее по предыдущим 5 барам (лаговым значениям). Записываю формулу в виде:
EURUSD = C(1)*EURUSD(-1) + C(2)*EURUSD(-2) + C(3)*EURUSD(-3) + C(4)*EURUSD(-4) + C(5)*EURUSD(-5)
2. Оценка
Необходимо оценить коэф с(i) этого уравнения так, чтобы кривая нашей МА как можно лучше соответствовала исходному ряду EURUSD_H1 за год. Получаем результат оценки неизвестных коэф.
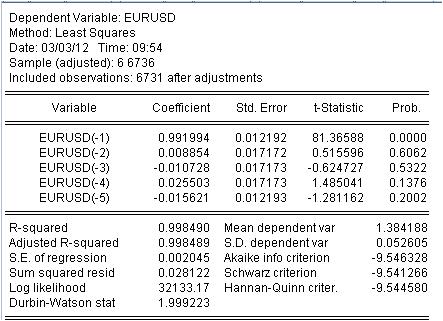
Получили значения коэф нашей взвешенной машки. Имеем уравнение:
EURUSD = 0.991993934254*EURUSD(-1) + 0.00885362355538*EURUSD(-2) - 0.0107282369642*EURUSD(-3) + 0.0255027160774*EURUSD(-4) - 0.0156205779585*EURUSD(-5)
3. Результаты.
Какие результаты мы видим?
3.1. Прежде всего само уравнение машки. При этом отмечу один нюанс. Когда вычисляем простую машку, поучая среднее, то это среднее мы записываем почему-то не в середину интервала а в его конец. По регресси мы вычисляем имеено последнее значение по предыдущим.
3.2. Выясняется, что коэф у машки не константы, а случайные величины! со своим отклонением.
3.3. Последний столбец говори, что имеется не нуевая вероятность того, что указанные коф вообще равны нулю.
4. Работа с уравнением
Посмотрим на нашу взвешенную машку.

Машка настолько плотно закрыла котир, что его не видно, но все-таки имеются расхождения между котиром и машкой. Вот статистики этих расхождений

Видим огромный разброс ошибки от -137 пипсов доя 215 пипсов. Хотя стандартное отклонение = 20 пипсам.
Вывод.
С помощью регрессии получили необыкновенно качественную машку с известными стат характеристиками.
Последнее. Юсуф! Не лезь под трамвай, не надо веселить публику еще на одно ветке.
Готов обсудить литературу и применение темы регрессия.
3. Результаты.
Какие результаты мы видим?
3.1. Прежде всего само уравнение машки. При этом отмечу один нюанс. Когда вычисляем простую машку, поучая среднее, то это среднее мы записываем почему-то не в середину интервала а в его конец. По регресси мы вычисляем имеено последнее значение по предыдущим.
3.2. Выясняется, что коэф у машки не константы, а случайные величины! со своим отклонением.
3.3. Последний столбец говори, что имеется не нуевая вероятность того, что указанные коф вообще равны нулю.
1. Извини за очередную порцию соли на рану - исходный ряд все равно нестационарен
2. Эта вероятность почти всегда ненулевая
3. На мультиколлинеарность проверял? ИМХО если устранишь мультиколлинеарность, то останется только одна переменная. Значимые факторы определял?
4. Сколько у тебя наблюдений на 5 переменных?
Откуда такой грамотный?
1. Извини за очередную порцию соли на рану - исходный ряд все равно нестационарен
Конечно, а другие нам не интересны
2. Эта вероятность почти всегда ненулевая
Не правда. Если ненулевая, то ошибка функциональной формы
3. На мультиколлинеарность проверял? ИМХО если устранишь мультиколлинеарность, то останется только одна переменная. Значимые факторы определял?
Что такое "значимые факторы" не понимаю, а вот коррелированность коэф прошу посмотреть.
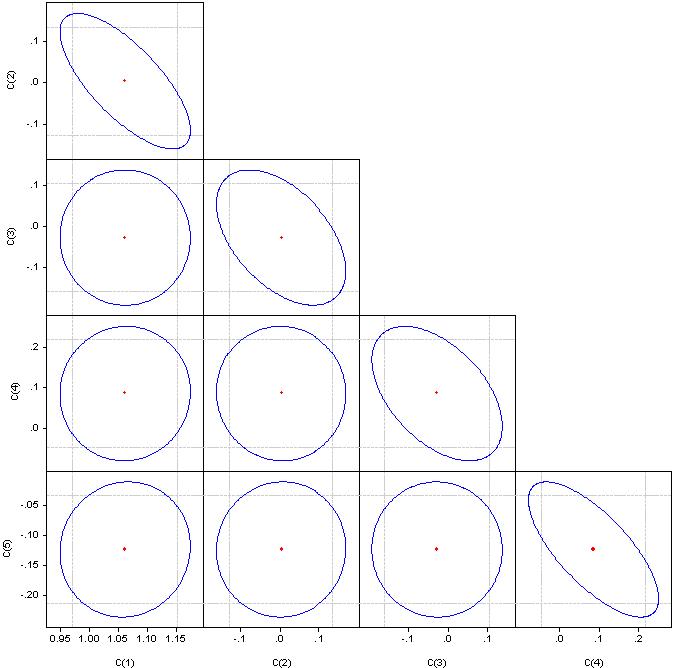
Если круг - корреляция нулевая. Если слилось в прямую линию - то корреляция между соответствующей парой коэф 100%
4. Сколько у тебя наблюдений на 5 переменных?
Наблюдений 6736
первый этап любой регрессионной модели - отбор факторов. Если ты не применяешь шаговую регрессию (с включениями или с исключениями), значит надо их отбирать вручную.
Мультиколлинеарность - тесная зависимость между факторными признаками, включенными в модель. Не коррелированность коэффициентов, а коррелированность факторов.
Наличие мультиколлинеарности приводит к:
- искажению величины параметров модели, которые имеют тенденцию к завышению;
- слабой обусловленности системы нормальных уравнений;
- осложнению процесса определения наиболее существенных факторных признаков.
Один из индикатор мультиколлинеарности - превышение парными коэффициентами корреляции величины 0.8. Тут факторы явно имеют сильную корреляцию. Что б ее устранить надо выкидывать избыточные факторы. Или вручную или шаговой регрессией.
Посмотри в пакете - шаговая регрессия или гребневая регрессия.
И 6736/4 - слишком большое количество наблюдений. Надо погуглить - не помню уже как определяется оптимальное количество наблюдений исходя из количества факторов.
Будьте так любезны, поучаствуйте в моих топиках по эконометрике.
Продолжим подбор литературы.
Следующая тема - лаги Алмона
Как было замечено выше имеются сложности с коэф регрессии, которые были вычислены методом наименьших квадратов. Возникла идея наложить дополнительные ограничения на коэф регрессии, в которых зависимая переменная определяется несколькими лаговыми значениями независимой переменной как в уравнении, приведенном выше.
Идея состоит в следующем: наложить ограничения на коэф при лаговых значениях таким образом, чтобы они подчинялись некоторому полиномиальному распределению. В EViews такой подход называют "полиномами распределенных лагов (PDL)". Выбор конкретной степени полинома определяется экспериментально.
Описан данный подход здесь.
Приведу практический пример.
Построим аналог машки с периодом 5, но коэф при барах должны располагаться на полиноме 3-го порядка.
В EViews это записывается следующим образом для EURUSD
EURUSD PDL(EURUSD(-1), 5,3)
В более привычном виде:
EURUSD = + C(5)*EURUSD(-1) + C(6)*EURUSD(-2) + C(7)*EURUSD(-3) + C(8)*EURUSD(-4) + C(9)*EURUSD(-5) + C(10)*EURUSD(-6)
Оценку коэффициентов производим МНК и получаем результат оценки коэффициентов:
EURUSD = + 0.934972661616*EURUSD(-1) + 0.139869148138*EURUSD(-2) - 0.093599954464*EURUSD(-3) - 0.0264992987207*EURUSD(-4) + 0.0801064628352*EURUSD(-5) - 0.0348473223286*EURUSD(-6)
Статистика по оценке уравнения выглядит следующим образом:
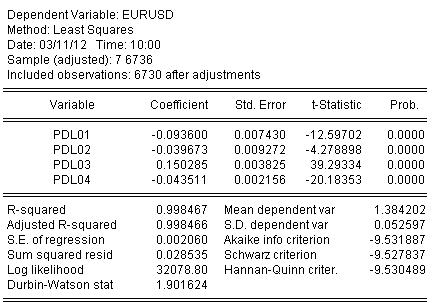
Из статистики мы видим очень хороший уровень отображения исходного котира нашей машкой от Алмона R-квадрат = 0.998467
Графически это выглядит как:

Регрессия (машка по Алмону) полностью закрыла исходных котир.
И последняя ложка меда.
Посмотрим, каков остаток, т.е. разность между нашей машкой от Алмона и исходным котиром. Очень важна стационарность/нестационарность этого остатка.

Тест единичного корня утверждает, что остаток стационарен.
Машки, которыми мы пользуемся, таким уровнем соответствия исходному котиру и свойством стационарности ошибки подгонки не обладают.
Хочу перенести из соседней ветки ссылки.
Эти ссылки относятся самой проблемной области - прогнозу.
Первая - это аттач. там имеется список литературы.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Если погуглить по слову "эконометрика", то получишь огромный список литературы, в котором трудно разобраться даже специалисту. В одной книге написано одно, в другой - другое, третья - просто компиляция первых друг с какими-то не точностями. Но подход "от книг" объединения не ясность применения этих книг на практике. Меня умствования, переходящие в ботаническую пургу не интересуют.
Аналогично иным спискам книг на этом форуме, например, по статистике, предлагаю коллективно составить список учебников, монографий, диссертаций, статей, интернет-ресурсов и пакетов программ, которые бы по мнению участников имеют отношение к измерению экономических данных - к эконометрике. При этом не будем забывать, что математическая статистика - это старшая сестра эконометрики. Предлагаю не включать в этот список, все что относится к техническому анализу.
Чтобы исключить скатывание в ботанику, предлагаю специфический подход к перечню и упорядочению списка литературы. Выкладываем ссылки (сами книги) только в том случае, если известны программы, реализующие алгоритмы из этих книгах. Для себя я этот круг сильно сузил и взял в качестве программы EViews. Эта программа не обладает никаким преимуществом перед другими, имеет свои достоинства и недостатки, но ее беру в качестве рубрикатора эконометрики. В аттаче приложил оглавление второго тома руководства пользователя, чтобы очертить сразу по возможности наиболее широкий круг проблем. Из-за предлагаемого поджхода выпало несколько направлений, используемых в эконометрике, но не входящих в EVIEWS, например, НС, вейвлеты и т.д. Естественно ссылки на подобные программы и книги к ним также приветствуются.
Если нам удастся не только привести ссылку на источник, алгоритм, но и произвести конкретные вычисления, то этой ветке цены не будет.
Номера глав из аттача предлагаю использовать для группировки книг.
Итак, прошу, поддерживайте.