Algoritmi di ottimizzazione della popolazione: Algoritmo del pipistrello (Bat - BA)

MetaTrader 5 — Esempi | 22 novembre 2023, 09:44

304

Andrey Dik

Contenuto

1. Introduzione
2. Descrizione dell'algoritmo
3. Risultati del test

1. Introduzione

I pipistrelli sono animali straordinari. Gli scienziati ritengono che i primi pipistrelli siano comparsi 65-100 milioni di anni fa, vivendo fianco a fianco con i dinosauri. I pipistrelli sono gli unici mammiferi alati. I pipistrelli vantano oltre 1300 specie. Si trovano quasi ovunque, tranne che nelle regioni polari. Durante il giorno si nascondono in rifugi. Per orientarsi nelle grotte buie e cacciare dopo il tramonto, i pipistrelli si basano sull’ecolocalizzazione, un sistema che consente loro di rilevare gli oggetti utilizzando le onde sonore. L'ecolocalizzazione avviene attraverso l'emissione di un suono ad alta frequenza che si muove in avanti fino a colpire un oggetto che poi viene rinviato. L'ecolocalizzazione è una sorta di sonar: un pipistrello emette un suono forte e brevemente pulsato. Quando il suono raggiunge un oggetto, l'eco ritorna alle orecchie del pipistrello dopo un breve periodo di tempo, è così che i pipistrelli si orientano nello spazio e determinano la posizione delle loro prede.

Il Bat Algorithm (BA) è un algoritmo euristico introdotto da Yang nel 2010 che imita il comportamento di ecolocalizzazione dei pipistrelli per eseguire un'ottimizzazione globale. La meta-euristica, solitamente ispirata alla natura e ai processi fisici, è oggi utilizzata come una delle tecniche più potenti per risolvere molti problemi di ottimizzazione complessi. L'ottimizzazione è la selezione degli elementi migliori per un certo insieme di criteri tra una serie di opzioni efficienti, che presenta diversi vantaggi e svantaggi in termini di efficienza computazionale e di probabilità di ottimizzazione globale.

L'ottimizzazione dell’elemento offre una struttura formale per modellare e risolvere una serie di problemi specifici, fornendo una funzione "target" che prende in ingresso un parametro. L'obiettivo è trovare il valore del parametro combinato che restituisca il valore migliore. Questa struttura è sufficientemente astratta da poter interpretare i vari problemi come problemi di "ottimizzazione dell’elemento".

Tuttavia, l'ottimizzazione tradizionale dell’elemento viene utilizzata solo per risolvere alcuni piccoli problemi, spesso non applicabili nella pratica. Per questo motivo, gli scienziati stanno rivolgendo la loro attenzione alla natura, che fornisce ricchi modelli per risolvere questi problemi. Prendendo a modello i sistemi biologici naturali, sono stati proposti molti algoritmi di ottimizzazione intelligenti a sciame per risolvere problemi applicati con metodi non convenzionali. Sono ampiamente utilizzati in vari problemi di ottimizzazione grazie alle loro eccellenti prestazioni. BA è un nuovo e moderno algoritmo di tipo a sciame che esegue un processo di ricerca utilizzando pipistrelli artificiali come agenti di ricerca simulando il volume naturale dell'impulso sonoro e la frequenza di emissione dei pipistrelli reali.

2. Descrizione dell'algoritmo

Nell'algoritmo di base dei pipistrelli, ogni pipistrello è trattato come una particella "senza massa e senza dimensioni" rappresentando una soluzione valida nello spazio delle soluzioni. Per le diverse funzioni di fitness, ogni pipistrello ha un valore dell’elemento corrispondente e determina l'individuo ottimale attuale confrontando i valori degli elementi. Quindi si aggiornano la frequenza dell'onda acustica, la velocità, la velocità di emissione degli impulsi e il volume di ogni pipistrello nella popolazione, si continua l'evoluzione iterativa, si approssima e si genera la soluzione ottimale corrente e infine si trova la soluzione ottimale globale. L'algoritmo aggiorna la frequenza, la velocità e la posizione di ogni pipistrello.

L'algoritmo standard richiede cinque parametri di base: frequenza, intensità, ondulazione e rapporto tra intensità e ondulazione. La frequenza viene utilizzata per bilanciare l'impatto della migliore posizione storica sulla posizione attuale. Un singolo pipistrello cercherà lontano dalla posizione storica del gruppo quando il raggio della frequenza di ricerca è ampio e viceversa.

Ci sono molti parametri nell'algoritmo rispetto a quelli considerati in precedenza:

input double MIN_FREQ_P = 0.0;
input double MAX_FREQ_P = 1.0;
input double MIN_LOUDNESS_P = 0,0;
input double MAX_LOUDNESS_P = 1,5;
input double MIN_PULSE_P = 0,0;
input double MAX_PULSE_P = 1,0;
input double ALPHA_P = 0,3;
input double GAMMA_P = 0,3;

Durante l'implementazione dell'algoritmo BA, mi sono imbattuto nel fatto che in molte fonti gli autori degli articoli descrivono l'algoritmo in modi completamente differenti. Le differenze riguardano sia l'uso dei termini nella descrizione dei punti chiave sia le caratteristiche fondamentali dell'algoritmo, per cui descriverò come l'ho inteso. I principi fisici di base sottostante dell'ecolocalizzazione possono essere applicati all'algoritmo con notevoli riserve e convenzioni. Si ipotizza che i pipistrelli utilizzino impulsi sonori con una frequenza compresa tra MinFreq e MaxFreq. La frequenza influisce sulla velocità del pipistrello. Viene utilizzato anche il concetto condizionale di intensità, che influisce sulla transizione dallo stato di ricerca locale nella posizione attuale del pipistrello a quello globale in prossimità della soluzione migliore. La frequenza di pulsazione aumenta durante l'ottimizzazione, mentre il volume dei suoni diminuisce.

Pseudo codice dell'algoritmo BA (Fig. 1):

1. Inizializzazione della popolazione dei pipistrelli.
2. Generazione della frequenza, velocità e nuove soluzioni.
3. Cercare una soluzione locale.
4. Aggiornamento della soluzione globale.
5. Diminuzione del volume e aumento della frequenza di pulsazione.
6. Ripetere il passaggio 2 fino a quando non viene soddisfatto il criterio di arresto.

schema

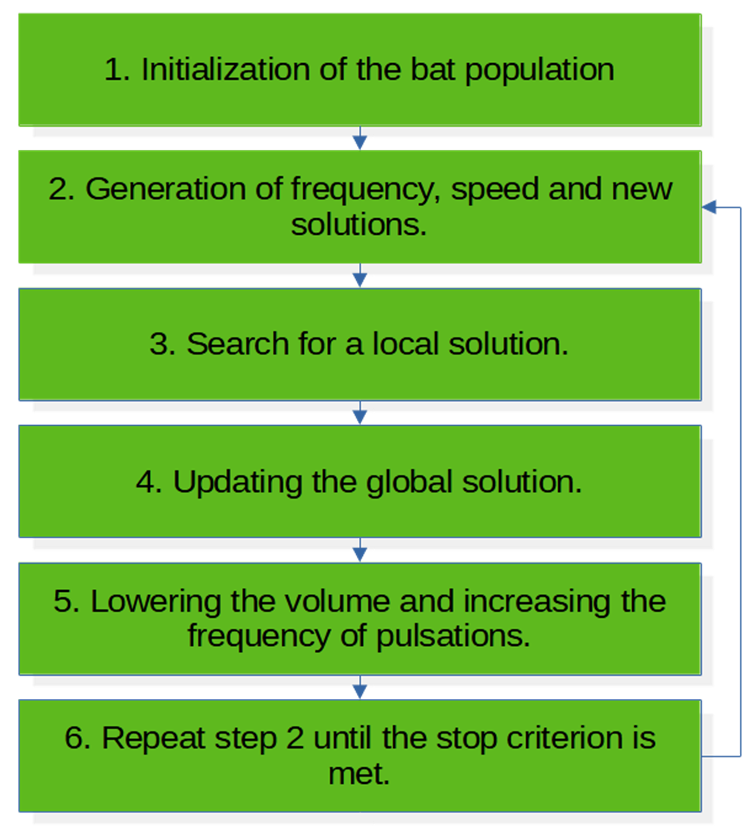
Fig. 1. Diagramma dell'algoritmo BA

Iniziamo a descrivere il codice. Per descrivere l'agente di ricerca "pipistrello", abbiamo bisogno di una struttura in cui descrivere tutte le caratteristiche necessarie per una descrizione completa dello stato al momento di ogni iterazione. L'array position [] è usato per memorizzare le coordinate della posizione migliore nello spazio, mentre l'array auxPosition [] è per le coordinate "operative" correnti. L’array speed [] è necessario per il calcolo del vettore della velocità in base alle coordinate. Frequency - frequenza degli impulsi sonori, initPulseRate - frequenza iniziale degli impulsi (individuale per ogni pipistrello fin dall'inizio dell'ottimizzazione), pulseRate - frequenza degli impulsi all'iterazione corrente, loudness - intensità degli impulsi sonori, fitness - valore funzione di fitness per tutte le iterazioni.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bat
{
  double position    [];
  double auxPosition [];
  double speed       [];
  double frequency;
  double initPulseRate;
  double pulseRate;
  double loudness;
  double fitness;
  double fitnessBest;
};
//——————————————————————————————————————————————————————————————————————————————

La classe dell'algoritmo bat include un array di strutture di agenti di ricerca, confini e passaggi dello spazio esplorato, le migliori coordinate trovate dall'algoritmo, il miglior valore della funzione di fitness e costanti per la memorizzazione dei parametri dell'algoritmo, oltre al metodo pubblico di inizializzazione, due metodi pubblici necessari per il funzionamento dell'algoritmo e metodi privati specifici dell'algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BA
{
  //============================================================================
  public: S_Bat  bats      []; //bats
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,
                     const int    batsNumberP,
                     const double min_FREQ_P,
                     const double max_FREQ_P,
                     const double min_LOUDNESS_P,
                     const double max_LOUDNESS_P,
                     const double min_PULSE_P,
                     const double max_PULSE_P,
                     const double alpha_P,
                     const double gamma_P,
                     const int    maxIterP);

  public: void Flight (int epoch);
  public: void Preparation ();

  //============================================================================
  private: void Walk               (S_Bat &bat);
  private: void AproxBest          (S_Bat &bat, double averageLoudness);
  private: void AcceptNewSolutions (S_Bat &bat);
  private: int  currentIteration;
  private: int  maxIter;

  private: double MIN_FREQ;
  private: double MAX_FREQ;

  private: double MIN_LOUDNESS;
  private: double MAX_LOUDNESS;

  private: double MIN_PULSE;
  private: double MAX_PULSE;

  private: double ALPHA;
  private: double GAMMA;

  private: int    params;
  private: int    batsNumber;

  private: bool   firstFlight;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Nel metodo pubblico Init () dell'algoritmo si impostano i parametri, si alloca la memoria per gli array, si ripristina la variabile al valore minimo per memorizzare il miglior fit e si reimposta il flag dell'iterazione iniziale. In generale, questo metodo non è complicato ed è qualcosa di speciale.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Init (const int    paramsP,
                    const int    batsNumberP,
                    const double min_FREQ_P,
                    const double max_FREQ_P,
                    const double min_LOUDNESS_P,
                    const double max_LOUDNESS_P,
                    const double min_PULSE_P,
                    const double max_PULSE_P,
                    const double alpha_P,
                    const double gamma_P,
                    const int    maxIterP)
{
  MathSrand (GetTickCount ());

  fB = -DBL_MAX;

  params       = paramsP;
  batsNumber   = batsNumberP;
  MIN_FREQ     = min_FREQ_P;
  MAX_FREQ     = max_FREQ_P;
  MIN_LOUDNESS = min_LOUDNESS_P;
  MAX_LOUDNESS = max_LOUDNESS_P;
  MIN_PULSE    = min_PULSE_P;
  MAX_PULSE    = max_PULSE_P;
  ALPHA        = alpha_P;
  GAMMA        = gamma_P;
  maxIter      = maxIterP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);

  firstFlight = false;

  ArrayResize (bats, batsNumber);

  for (int i = 0; i < batsNumber; i++)
  {
    ArrayResize (bats [i].position,    params);
    ArrayResize (bats [i].auxPosition, params);
    ArrayResize (bats [i].speed,       params);

    bats [i].fitness  = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

Il primo metodo chiamato a ogni iterazione è Flight(). Concentra la struttura principale della logica di ricerca, mentre il resto dei dettagli sono collocati in metodi specifici privati ausiliari per questo algoritmo di ottimizzazione. Alla prima iterazione, il flag firstFlight viene azzerato (l'azzeramento avviene durante l'inizializzazione nel metodo Init ()). Questo significa che dobbiamo assegnare uno stato iniziale a ogni pipistrello, che è una posizione casuale nello spazio di ricerca:

velocità zero,
frequenza individuale degli impulsi sonori assegnata da un numero casuale nell'intervallo specificato dai parametri,
frequenza di pulsazione individuale iniziale, anch'essa definita da un numero casuale nell'intervallo nei parametri
e l'intensità degli impulsi sonori nell'intervallo dei parametri.

Come si può vedere, ogni pipistrello artificiale ha una serie individuale di caratteristiche dei segnali sonori, che li rende più simili ai pipistrelli reali in natura. Nell'intera popolazione, che può essere composta da diverse centinaia di migliaia di individui, una madre può individuare un singolo cucciolo grazie alla singolare firma sonora che il piccolo emette.

Se il flag firstFlight è abilitato, è necessario eseguire le operazioni di base per spostare i pipistrelli. Una delle caratteristiche interessanti dell'algoritmo risiede nel concetto di intensità sonora media dell'intera popolazione. In generale, l'intensità del suono diminuisce tramite il coefficiente "alfa" durante tutte le iterazioni. Qui ci sono due tipi di movimento del pipistrello: Walk () - movimento individuale con calcolo del vettore velocità per ogni componente delle coordinate e movimento locale in prossimità della soluzione migliore.

Ad ogni iterazione successiva, l'intensità delle pulsazioni diminuisce, influenzando l'intensità dell'esplorazione dei dintorni. Pertanto, l'esplorazione e lo sfruttamento cambiano dinamicamente durante l'ottimizzazione. Successivamente, vedremo come l'iterazione corrente influisce sul comportamento dei pipistrelli.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Flight (int epoch)
{
  currentIteration = epoch;

  //============================================================================
  if (!firstFlight)
  {
    fB = -DBL_MAX;

    //--------------------------------------------------------------------------
    for (int b = 0; b < batsNumber; b++)
    {
      for (int p = 0; p < params; p++)
      {
        bats [b].position    [p] = RNDfromCI (rangeMin [p], rangeMax [p]);
        bats [b].position    [p] = SeInDiSp (bats [b].position [p], rangeMin [p], rangeMax [p], rangeStep [p]);
        bats [b].auxPosition [p] = bats [b].position    [p];
        bats [b].speed       [p] = 0.0;
        bats [b].frequency       = RNDfromCI (MIN_FREQ, MAX_FREQ);
        bats [b].initPulseRate   = RNDfromCI (MIN_PULSE, MAX_PULSE / 2);
        bats [b].pulseRate       = bats [b].initPulseRate;
        bats [b].loudness        = RNDfromCI (MAX_LOUDNESS / 2, MAX_LOUDNESS);
        bats [b].fitness         = -DBL_MAX;
        bats [b].fitnessBest     = -DBL_MAX;
      }
    }

    firstFlight = true;
  }
  //============================================================================
  else
  {
    double avgLoudness = 0;

    for (int b = 0; b < batsNumber; b++)
    {
      avgLoudness += bats [b].loudness;
    }

    avgLoudness /= batsNumber;

    for (int b = 0; b < batsNumber; b++)
    {
      Walk (bats [b]);

      if (RNDfromCI (MIN_PULSE, MAX_PULSE) > bats [b].pulseRate)
      {
        AproxBest (bats [b], avgLoudness);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il secondo metodo pubblico richiesto, chiamato a ogni iterazione - Preparation() è necessario per aggiornare la migliore soluzione globale. Qui possiamo vedere come viene utilizzato il concetto di "intensità". Poiché ad ogni iterazione il volume di ciascun pipistrello diminuisce tramite un fattore (parametro di regolazione dell'algoritmo "alfa"), la probabilità di uno studio locale diminuisce insieme all'intensità dello studio della soluzione globale. In altre parole, la probabilità di aggiornare la posizione migliore di ogni pipistrello diminuisce a ogni iterazione. Questo è uno di quei momenti dell'algoritmo meno compresi, almeno per me. Tuttavia, l'autore dell'algoritmo lo ha implementato, il che significa che è necessario.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Preparation ()
{
  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (bats [b].fitness > fB)
    {
      fB = bats [b].fitness;
      ArrayCopy (cB, bats [b].auxPosition, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int b = 0; b < batsNumber; b++)
  {
    if (RNDfromCI (MIN_LOUDNESS, MAX_LOUDNESS) < bats [b].loudness && bats [b].fitness >= bats [b].fitnessBest)
    {
      AcceptNewSolutions (bats [b]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il metodo privato Walk() assicura che ogni pipistrello si muova individualmente rispetto alla sua migliore posizione attuale, data la migliore soluzione globale. Questo metodo utilizza la frequenza degli impulsi sonori, che varia in modo casuale all'interno dell'intervallo [MIN_FREQ;MAX_FREQ]. La frequenza è necessaria per calcolare la velocità di movimento dell'agente di ricerca, che è il prodotto della frequenza per la differenza tra la migliore posizione del pipistrello e la migliore soluzione globale. Successivamente, dal vettore, il valore della velocità viene aggiunto alla migliore soluzione attuale del vettore pipistrello. Quindi, operiamo con quantità fisiche sproporzionate, ma cosa possiamo fare? Si tratta solo di un'approssimazione agli oggetti fisici reali. In questo caso la plausibilità deve essere trascurata. Dopo aver calcolato la nuova posizione, è necessario verificare che le coordinate non siano out-of-range utilizzando il metodo SeInDiSp ().

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::Walk (S_Bat &bat)
{
  for (int j = 0; j < params; ++j)
  {
    bat.frequency       = MIN_FREQ + (MAX_FREQ - MIN_FREQ) * RNDfromCI (0.0, 1.0);
    bat.speed       [j] = bat.speed [j] + (bat.position [j] - cB [j]) * bat.frequency;
    bat.auxPosition [j] = bat.position [j] + bat.speed [j];

    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Il secondo metodo privato, AproxBest(), è responsabile dello spostamento dei pipistrelli rispetto alla soluzione migliore globale, fornendo un ulteriore perfezionamento delle coordinate. Non mi è possibile comprendere il significato fisico di questa azione, che consiste nell'aggiunta, vettore per vettore alle coordinate dell'incremento sotto forma di intensità media dell'intera popolazione di pipistrelli moltiplicato per un numero casuale nell'intervallo [-1,0; 1,0]. Ho provato a ridurre i valori alla dimensione della funzione da ottimizzare attraverso il vettore dei valori validi del dominio di definizione, ma i risultati dei test si sono rivelati peggiori della versione dell'algoritmo dell'autore, quindi ho lasciato tutto com'è, ma sono sicuro che l'efficienza dell'algoritmo BA può essere migliorata, ma questo richiederà ulteriori ricerche, che non erano l'obiettivo in questo caso. Dopo aver calcolato le coordinate, i valori vengono controllati per verificare che non siano out-of-range con il metodo SeInDiSp ().

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AproxBest (S_Bat &bat, double averageLoudness)
{
  for (int j = 0; j < params; ++j)
  {
    bat.auxPosition [j] = cB [j] + averageLoudness * RNDfromCI (-1.0, 1.0);
    bat.auxPosition [j] = SeInDiSp (bat.auxPosition [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Un altro metodo privato specifico è AcceptNewSolutions (), che viene richiamato quando viene soddisfatta la condizione di test per la frequenza degli impulsi sonori di ciascun pipistrello. La nuova migliore soluzione individuale viene accettata, così come l’intensità individuale e la frequenza di pulsazione individuale vengono ricalcolati qui. Qui possiamo vedere come il numero ordinale di un'iterazione sia coinvolto nel calcolo della frequenza di pulsazione.

A questo punto della logica dell'algoritmo, mi sono preso qualche libertà e ho cambiato la logica, rendendo il risultato indipendente dalla dimensione del numero totale di iterazioni, il che alla fine ha aumentato leggermente l'efficienza dell'algoritmo. Nella versione originale, il numero di iterazioni era direttamente coinvolto nella formula non lineare per il calcolo della frequenza degli impulsi. BA già dispone di un sacco di convenzioni. Non potevo chiudere gli occhi su un altro caso.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BA::AcceptNewSolutions (S_Bat &bat)
{
  ArrayCopy(bat.position, bat.auxPosition, 0, 0, WHOLE_ARRAY);
  bat.fitnessBest = bat.fitness;
  bat.loudness    = ALPHA * bat.loudness;
  double iter     = Scale (currentIteration, 1, maxIter, 0.0, 10.0, false);
  bat.pulseRate   = bat.initPulseRate *(1.0 - exp(-GAMMA * iter));
}
//——————————————————————————————————————————————————————————————————————————————

La dipendenza della frequenza di pulsazione dal numero dell'iterazione corrente (x nel grafico) e dal parametro di impostazione GAMMA è illustrata nella Figura 2.

gamma

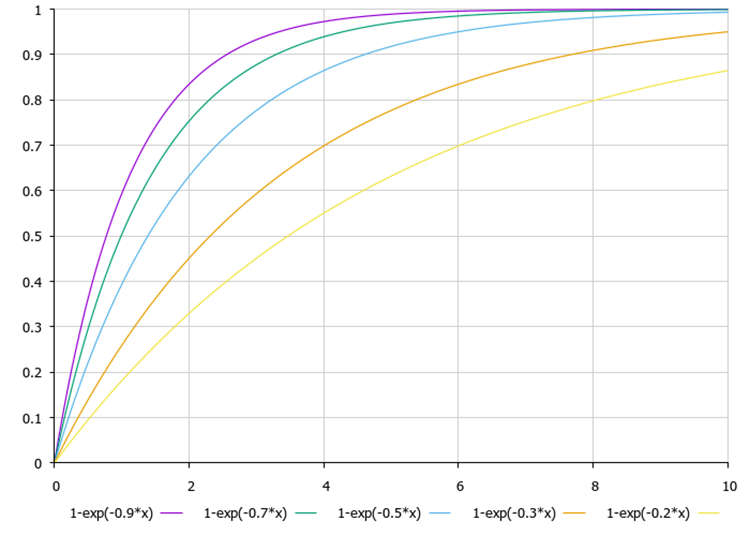
Figura 2. Dipendenza della frequenza di pulsazione dal numero dell'iterazione corrente e dal parametro di impostazione GAMMA con i valori di 0,9, 0,7, 0,5, 0,3, 0,2

3. Risultati del test

Nell'ultimo articolo ho accennato all'intenzione di rivedere la metodologia di calcolo del punteggio degli algoritmi testati. In primo luogo, poiché la maggior parte degli algoritmi possono facilmente far fronte alle funzioni di test a due variabili e la differenza tra i risultati è quasi indistinguibile, ho deciso di aumentare il numero di variabili per i primi due test su tutte le funzioni di test. Ora il numero di variabili sarà 10, 50 e 1000.

In secondo luogo, la funzione test Skin è stata sostituita con l’ampiamente utilizzata funzione Rastrigin (Figura 3). Questa funzione è regolare come la Skin. Ha una superficie complessa con molti estremi locali, un massimo globale in quattro punti e un minimo globale al centro degli assi delle coordinate.

In terzo luogo, ho deciso di normalizzare i risultati del test in un intervallo di valori tra tutti gli algoritmi della tabella, dove il risultato migliore è 1,0 e il risultato peggiore è 0,0. Questo ci permette di valutare in modo uniforme i risultati dei test, mentre la complessità delle funzioni viene presa in considerazione in base ai risultati di ciascuno degli algoritmi di ottimizzazione in test.

Successivamente, vengono riassunti i risultati dei test degli algoritmi. Al risultato massimo viene assegnato il valore 100 (risultato massimo di riferimento), mentre al valore minimo il valore è 1. Questo ci permette di confrontare direttamente gli algoritmi tra loro, anche considerando la complessità delle funzioni di test. Ora i risultati stampati in Print () vengono salvati rispettivamente nei file sorgente degli script di test per ciascun algoritmo. Lo script che calcola i punteggi dei test è allegato di seguito. Sarà aggiornato in articoli successivi con l'aggiunta dei risultati dei nuovi algoritmi considerati.

rastrigin

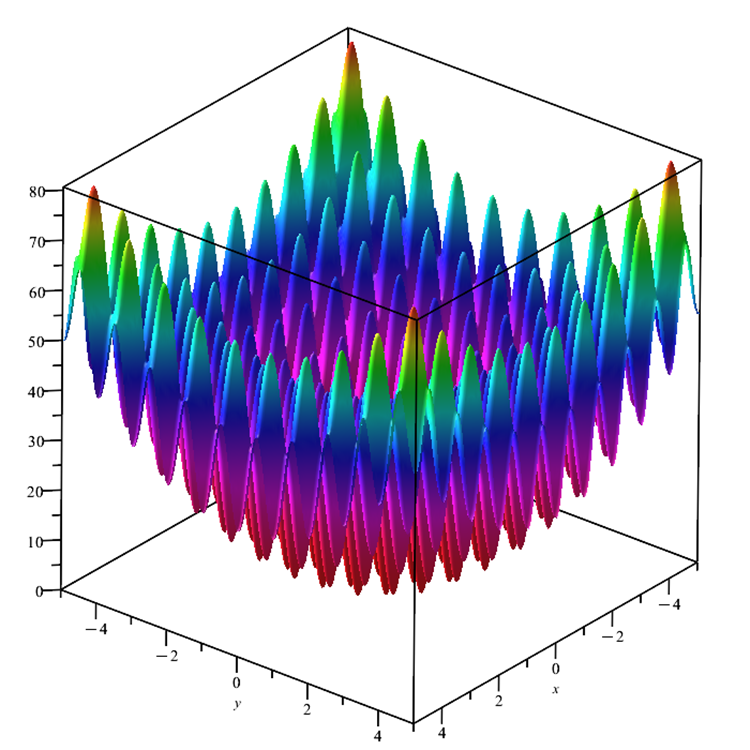
Fig. 3. Funzione test Rastrigin

I risultati del banco di prova sono i seguenti:

2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    C_AO_BA:50;0.0;1.0;0.0;1.5;0.0;1.0;0.3;0.3
2022.12.28 17:13:46.384    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 66.63334336098077
2022.12.28 17:13:48.451    Test_AO_BA (EURUSD,M1)    Score: 0.82562
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 65.51391114042588
2022.12.28 17:13:52.630    Test_AO_BA (EURUSD,M1)    Score: 0.81175
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 59.84512760590815
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    Score: 0.74151
2022.12.28 17:14:27.234    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    5 Forest's; Func runs 10000 result: 0.5861602092218606
2022.12.28 17:14:32.280    Test_AO_BA (EURUSD,M1)    Score: 0.33156
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.2895682720055589
2022.12.28 17:14:39.204    Test_AO_BA (EURUSD,M1)    Score: 0.16379
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.09867854051596259
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    Score: 0.05582
2022.12.28 17:15:14.716    Test_AO_BA (EURUSD,M1)    =============================
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 3.3199999999999994
2022.12.28 17:15:20.843    Test_AO_BA (EURUSD,M1)    Score: 0.27667
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 1.2079999999999997
2022.12.28 17:15:26.624    Test_AO_BA (EURUSD,M1)    Score: 0.10067
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.40759999999999996
2022.12.28 17:16:05.013    Test_AO_BA (EURUSD,M1)    Score: 0.03397

L'algoritmo bat ha mostrato risultati impressionanti sulla funzione regolare Rastrigin. È interessante notare che con l'aumento del numero di variabili nella funzione, la stabilità (ripetibilità) dei risultati aumenta, il che indica un'eccellente scalabilità di BA su funzioni regolari. In particolare, BA si è rivelato il migliore sulla funzione Rastrigin con 50 e 1000 variabili tra tutti i partecipanti al test, il che ci permette di raccomandare l'algoritmo bat per lavorare con funzioni regolari complesse e reti neurali. Sulle funzioni Forest e Megacity, l'algoritmo bat ha mostrato risultati medi, dimostrando la tendenza a bloccarsi su estremi locali. Le coordinate sono localizzate in gruppi e non mostrano la dinamica del cambiamento e del movimento verso l'optimum globale. Credo che questo accada perché l'algoritmo è sensibile alla presenza di un gradiente sulla superficie della funzione in esame. In assenza del gradiente, l'algoritmo si ferma rapidamente in prossimità delle aree locali che non presentano un incremento significativo dei valori della funzione di fitness. Inoltre, l'algoritmo BA manca di meccanismi che permettano di "saltare" in nuove aree sconosciute, simili al meccanismo implementato in COA (voli di Levy).

Vorrei anche menzionare un gran numero di impostazioni per il BA. Non solo ci sono molti parametri (gradi di libertà), ma ognuno di essi influisce notevolmente sia sulla natura delle proprietà di ricerca sia sui tassi di convergenza complessivi. Alcuni parametri possono dare risultati eccellenti su funzioni regolari, altri su funzioni discrete e fessurate. Trovare alcuni parametri universali che permettano di gestire allo stesso modo diversi tipi di funzioni di test è un compito difficile. L'articolo contiene il codice sorgente dell'algoritmo bat con i parametri che mi sembrano i più ottimali. In generale, sconsiglio l'uso di BA agli utenti che hanno poca esperienza nel lavoro con gli algoritmi di ottimizzazione, poiché i risultati dell'ottimizzazione possono variare notevolmente.

rastrigin

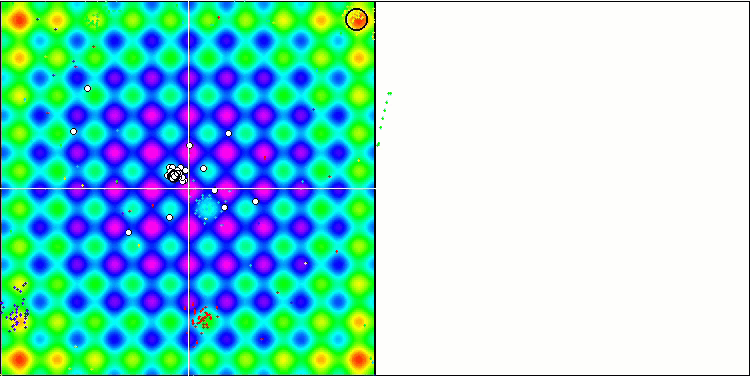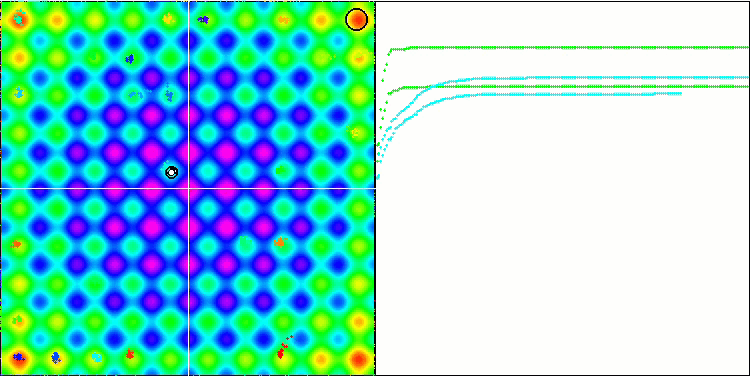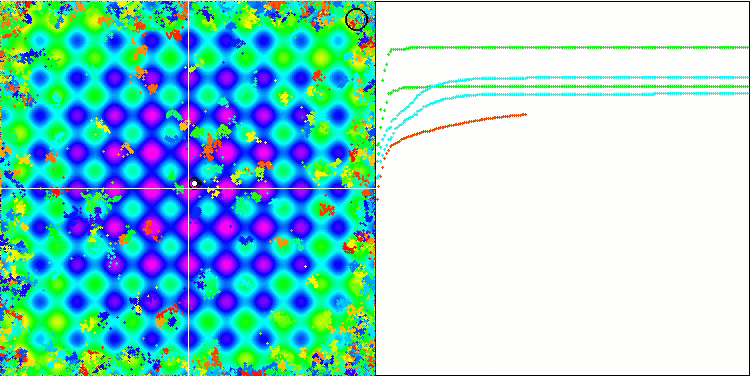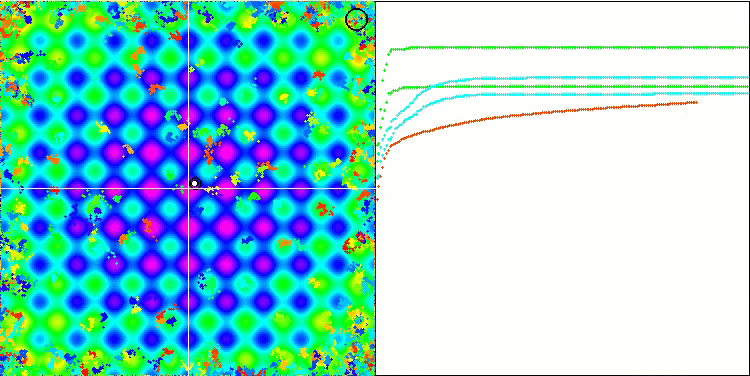
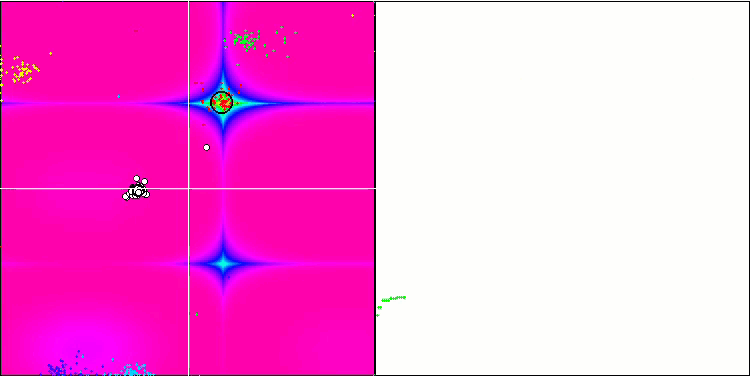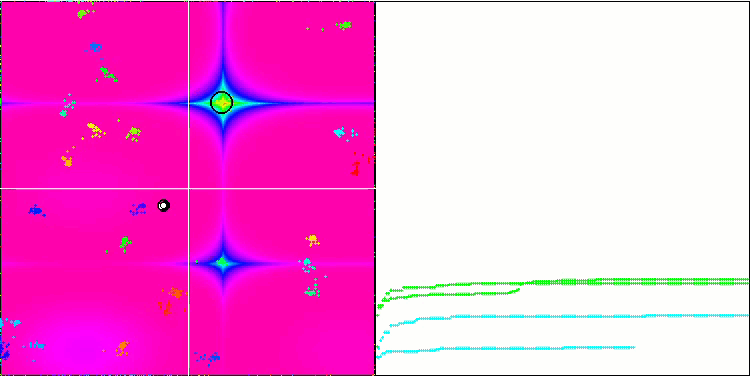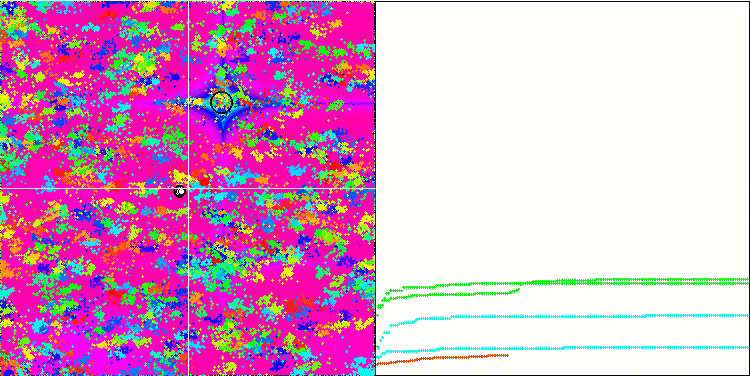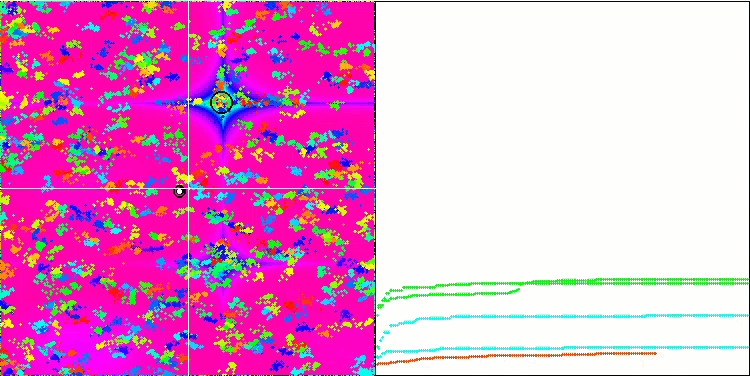
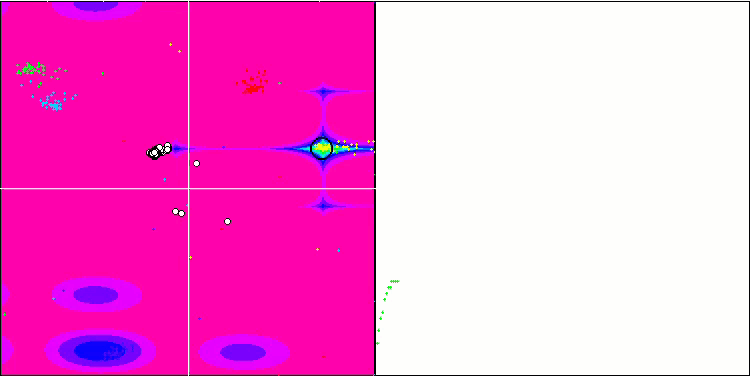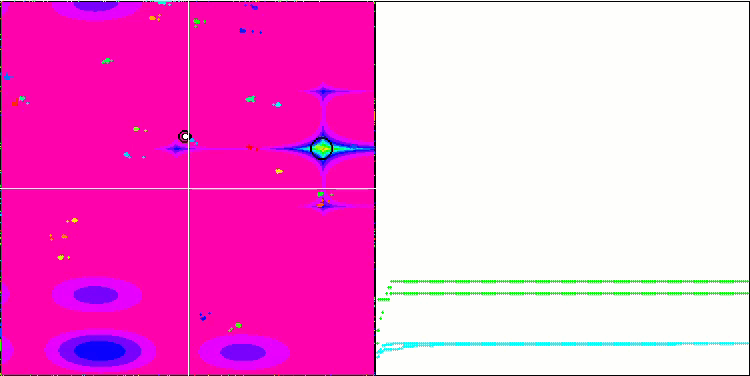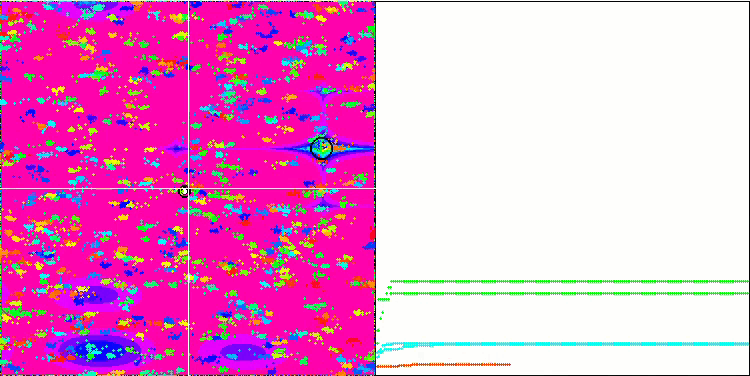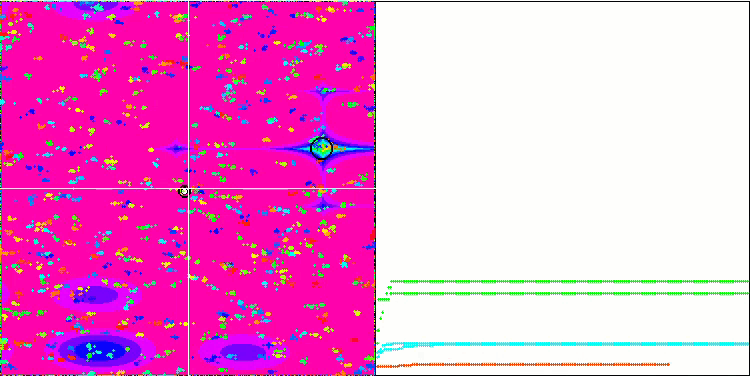
BA sulla funzione di test Rastrigin

forest

BA sulla funzione test Forest

megacity

BA sulla funzione test Megacity

Concentrandosi sulla visualizzazione delle funzioni di test, si può avere un'idea delle caratteristiche dell'algoritmo bat. In particolare, quando lavora su tutte le funzioni di test, l'algoritmo è caratterizzato dal raggruppamento delle coordinate in aree locali molto piccole. Mentre per una funzione regolare questa caratteristica permette di muoversi anche dove il gradiente della funzione di fitness cambia leggermente, su una funzione discreta questa caratteristica si rivela uno svantaggio, poiché l'algoritmo si blocca rimanendo piatto.

Risultati ottenuti dallo script che calcola i punteggi degli algoritmi di ottimizzazione:

2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_RND=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18210 | 0.15281 | 0.07011 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08623 | 0.04810 | 0.06094 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.08904 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.6893397068905002
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_PSO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.22131 | 0.12861 | 0.05966 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15345 | 0.10486 | 0.28099 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.08028 | 0.02385 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.053004072893302
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ACOm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.37458 | 0.28208 | 0.17991 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 1.00000 | 0.10959 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_ABC=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.84599 | 0.51308 | 0.22588 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.58850 | 0.21455 | 0.17249 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.47444 | 0.26681 | 0.35941 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.661160435265267
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_GWO=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.00000 | 0.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.18977 | 0.04119 | 0.01802 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_COAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.00000 | 0.73390 | 0.28892 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64504 | 0.34034 | 0.21362 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.67153 | 0.34273 | 0.45422 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.690306586791184
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FSS=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.50663 | 0.39737 | 0.11006 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.07806 | 0.05013 | 0.08423 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.00000 | 0.01084 | 0.18998 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    1.4272897567648186
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_FAm=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.64746 | 0.53292 | 0.18102 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.55408 | 0.42299 | 0.64360 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.21167 | 0.28416 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    4.477897116029613
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    =======C_AO_BA=======
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.43859 | 1.00000 | 1.00000 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.17768 | 0.17477 | 0.33595 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.15329 | 0.07158 | 0.46287 |
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    3.8147314003892507
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    ================
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    0.24898721240154956 | 5.946151922377553
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_RND: 8.652
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_PSO: 14.971
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ACOm: 100.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_ABC: 60.294
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_GWO: 1.000
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_COAm: 78.177
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FSS: 21.475
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_FAm: 74.486
2023.01.03 17:55:57.386    CalculationTestResults (EURUSD,M1)    C_AO_BA: 62.962

Diamo un'occhiata alla tabella di valutazione finale. Come già detto, la metodologia di calcolo delle caratteristiche stimate degli algoritmi è cambiata, quindi gli algoritmi hanno assunto una nuova posizione. Alcuni algoritmi classici sono stati rimossi dalla tabella e sono state lasciate solo le loro versioni modificate, che dimostrano prestazioni più elevate nei test. Ora i risultati del test non sono assoluti come in precedenza (risultati assoluti normalizzati dei valori della funzione di test), ma relativi, basati sui risultati del confronto tra gli algoritmi.

La tabella mostra che ACOm (Ottimizzazione della Colonia di Formiche) è attualmente leader. L'algoritmo ha mostrato i risultati migliori in cinque dei nove test, quindi il risultato finale è di 100 punti. COAm, una versione modificata dell'algoritmo di ottimizzazione del cucù, è al secondo posto. Questo algoritmo si è rivelato il migliore sulla funzione regolare Rastrigin e ha mostrato buoni risultati anche su altri test rispetto ad altri partecipanti. L'algoritmo della Lucciola modificato FAm ha conquistato il terzo posto. Ha mostrato i migliori risultati sulla funzione discreta Megacity. Solo l'FSS ha mostrato lo stesso risultato in questo test.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
AO	Descrizione	10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)	Finale Rastrigin	10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)	Finale Forest	10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)	Finale Megacity	Risultato finale
ACOm	ottimizzazione della colonia di formiche M	0.37458	0.28208	0.17991	0.83657	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.10959	2.10959	100.000
COAm	algoritmo di ottimizzazione a cucù M	1.00000	0.73390	0.28892	2.02282	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.45422	1.46848	78.177
FAm	algoritmo della lucciola M	0.64746	0.53292	0.18102	1.36140	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	74.486
BA	algoritmo del pipistrello	0.43859	1.00000	1.00000	2.43859	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.46287	0.68774	62.962
ABC	colonia di api artificiali	0.84599	0.51308	0.22588	1.58495	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.35941	1.10066	60.294
FSS	ricerca del banco di pesci	0.64746	0.53292	0.18102	1.36140	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	21.475
PSO	ottimizzazione dello sciame di particelle	0.22131	0.12861	0.05966	0.40958	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.00000	0.10413	14.971
RND	casuale	0.18210	0.15281	0.07011	0.40502	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.08904	0.08904	8.652
GWO	ottimizzazione del lupo grigio	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.01802	0.24898	1.000

Istogramma dei risultati dei test dell'algoritmo in Figura 4

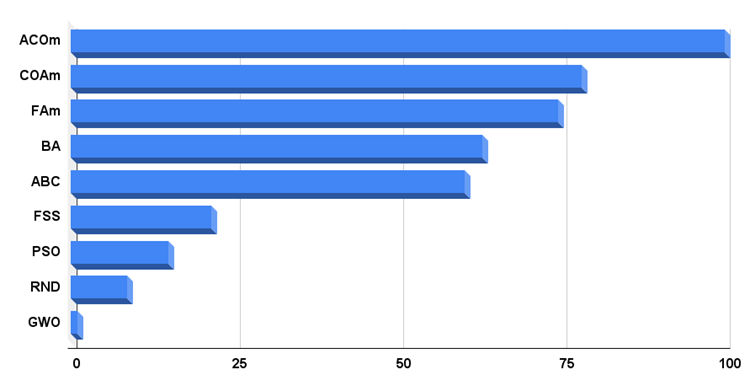
Fig. 4. Istogramma dei risultati finali degli algoritmi di test

Conclusioni sulle proprietà dell'algoritmo Bat (BA):

Pro:
1. Alta velocità.
2. L'algoritmo funziona bene con le funzioni regolari.
3. Scalabilità.

Contro:
1. Troppe impostazioni.
2. Risultati mediocri sulle funzioni discrete.

Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/11915

File allegati |

Scarica ZIP

9_The_world_of_AO_gBAs.zip (68.81 KB)

Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

Altri articoli di questo autore

Vai alla discussione

Impara come progettare un sistema di trading tramite Accelerator Oscillator

Un nuovo articolo della nostra serie su come creare semplici sistemi di trading tramite gli indicatori tecnici più popolari. Ne impareremo uno nuovo, che è l'indicatore Accelerator Oscillator, e impareremo a progettare un sistema di trading che lo utilizzi.

Algoritmi di ottimizzazione della popolazione: Algoritmo della Lucciola (Firefly FA)

In questo articolo prenderò in considerazione il metodo di ottimizzazione dell'Algoritmo Firefly(FA). Grazie alla modifica, l'algoritmo si è trasformato da outsider a vero leader della classifica.

Imparare come progettare un sistema di trading con l’Alligator

In questo articolo completeremo la nostra serie su come progettare un sistema di trading basato sugli indicatori tecnici più popolari. Impareremo a creare un sistema di trading basato sull'indicatore Alligator.

Come utilizzare i modelli ONNX in MQL5

ONNX (Open Neural Network Exchange) è un formato aperto creato per rappresentare modelli di machine learning. In questo articolo considereremo come creare un modello CNN-LSTM per prevedere le serie temporali finanziarie. Mostreremo anche come utilizzare il modello ONNX creato in un Expert Advisor MQL5.