Cálculo de diferencias, ejemplos.

Aleksey Panfilov 2018.01.10 16:14

Propongo recopilar indicadores y expertos en cálculo de diferencias en este hilo, en el código abierto.

Si hay interés, acabaremos construyendo o dibujando algo útil. :)

He reescrito el indicador en una versión más clara como ejemplo:

//|                                Copyright 2016, Aleksey Panfilov. |
//|                                                filpan1@yandex.ru |
//+------------------------------------------------------------------+
#property copyright "Copyright © 2018, Aleksei Panfilov. filpan1@yandex.ru"
#property link      "filpan1@yandex.ru"
#property version   "1.2"
#property description    "2018_01_10_Polynom_s4_s2_p72"
#property strict

#include <MovingAverages.mqh>


#property indicator_chart_window
#property indicator_buffers 6
#property indicator_plots   2
//--- plot a1_
#property indicator_label1  "MACD"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrSilver
#property indicator_style1  STYLE_SOLID
#property indicator_width1  2
//--- plot a2_
#property indicator_label2  "Signal"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
//--- plot a3_
#property indicator_label3  "Fast_line_1"
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrBlueViolet
#property indicator_style3  STYLE_SOLID
#property indicator_width3  6
//--- plot a4_
#property indicator_label4  "Fast_line_2"
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  1
//--- plot a5_
#property indicator_label5  "Slow_line_1"
#property indicator_type5   DRAW_LINE
#property indicator_color5  clrDarkGreen
#property indicator_style5  STYLE_SOLID
#property indicator_width5  4
//--- plot a6_
#property indicator_label6  "Slow_line_2"
#property indicator_type6   DRAW_LINE
#property indicator_color6  clrRed
#property indicator_style6  STYLE_SOLID
#property indicator_width6  1//--- input parameters

//         int   LIN_1_STEP    =4; //line_1_power
//input int      LIN_1_PLECHO  =72; //Fast_line_1_leverage
//         int   LIN_2_STEP    =2;//line_2_power
//input int      LIN_2_PLECHO  =78; //Fast_line_2_leverage
//         int   LIN_3_STEP    =4;//line_3_power
//input int      LIN_3_PLECHO  =72; //Slow_line_1_leverage
//         int   LIN_4_STEP    =2;//Slow_line_4_power
//input int      LIN_4_PLECHO  =72;//Slow_line_2_leverage

input        int TOCHKA_VHODA = 300;// start_point
//input int           base  =450;
      int   point_shift_1 = 0;
      int   point_shift_2 = 0;
//input int   Multiplikator = 10;
//input int   InpSignalSMA  = 9;  // Signal SMA Period



//--- indicator buffers

double a1_Buffer[];
double a2_Buffer[];
double a3_Buffer[];
double a4_Buffer[];
double a5_Buffer[];
double a6_Buffer[];
//double a7_Buffer[];
//double a8_Buffer[];
/**/


//===========================================================================================
   double Znach;


//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
 
//--- indicator buffers mapping
   SetIndexBuffer(0,a5_Buffer,INDICATOR_DATA);
   SetIndexBuffer(1,a6_Buffer,INDICATOR_DATA);
   SetIndexBuffer(2,a1_Buffer,INDICATOR_DATA);
   SetIndexBuffer(3,a2_Buffer,INDICATOR_DATA);
   SetIndexBuffer(4,a3_Buffer,INDICATOR_DATA);
   SetIndexBuffer(5,a4_Buffer,INDICATOR_DATA);
//----
//----
   SetIndexShift(2,-72);
   SetIndexShift(5,20);

//    if(TOCHKA_VHODA <= (LIN_1_PLECHO+25)*LIN_1_INTERVAL) TOCHKA_VHODA=(LIN_1_PLECHO+25)*LIN_1_INTERVAL;  
//    if(TOCHKA_VHODA <= (LIN_2_PLECHO+25)*LIN_2_INTERVAL) TOCHKA_VHODA=(LIN_2_PLECHO+25)*LIN_2_INTERVAL;  
//    if(TOCHKA_VHODA <= (LIN_3_PLECHO+25)*LIN_3_INTERVAL) TOCHKA_VHODA=(LIN_3_PLECHO+25)*LIN_3_INTERVAL;  
//    if(TOCHKA_VHODA <= (LIN_4_PLECHO+25)*LIN_4_INTERVAL) TOCHKA_VHODA=(LIN_4_PLECHO+25)*LIN_4_INTERVAL;  
//    if(TOCHKA_VHODA <= (base*2+25))                      TOCHKA_VHODA=(base*2+25);  

//------
//===========================================================================================
//===========================================================================================

   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {

   int i,z,limit;
//   int Bars=Bars(_Symbol,_Period);

   if(prev_calculated==0)// first calculation    
     {
      limit=rates_total-TOCHKA_VHODA;
      //--- set empty value for first limit bars
//Print("Bars=",Bars," rates_total=",rates_total," TOCHKA=",TOCHKA_VHODA," limit=",limit);
      if(limit<1)return(0);
      for(i=rates_total-1;i>=limit;i--)
      {
       a1_Buffer[i]=open[limit+1];
       a2_Buffer[i]=open[limit+1];
       a3_Buffer[i]=open[limit+1];
       a4_Buffer[i]=open[limit+1];
       a5_Buffer[i]=open[limit+1];
       a6_Buffer[i]=open[limit+1];
      }

     }
   else limit=rates_total-prev_calculated;
//--- main loop
   for(i=limit;i>=0 && !IsStopped();i--)
   {
//===========================================================================================
   Znach = 0; //iMA(NULL,0,base*2,0,MODE_SMA,PRICE_OPEN,i);
//===========================================================================================

 
      a1_Buffer[i]=((open[i] - Znach)    +5061600*a1_Buffer[i+1 ]-7489800   *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;

      a2_Buffer[i]=  3160*a1_Buffer[i]   -6240   *a1_Buffer[i+1 ]    +  3081*a1_Buffer[i+2 ];

      a4_Buffer[i+92]=a1_Buffer[i];   if(i<=10) { for(z=92-1;z>=0;z--){        a4_Buffer[i+0+z]=  5*a4_Buffer[i+1+z]  -  10*a4_Buffer[i+2+z]   +   10*a4_Buffer[i+3+z]  -  5*a4_Buffer[i+4+z]  +  1*a4_Buffer[i+5+z];  }}


//      a3_Buffer[i]=((open[i] - Znach)    +5061600*a3_Buffer[i+1 ]-7489800    *a3_Buffer[i+2 ]+4926624*a3_Buffer[i+3 ]-1215450*a3_Buffer[i+4 ])/1282975;

//      a4_Buffer[i]=  2701*a3_Buffer[i]   -5328   *a3_Buffer[i+1 ]    +  2628 *a3_Buffer[i+2 ];



//================================================================================================================================================================================================
//================================================================================================================================================================================================

//   a5_Buffer[i] = (a2_Buffer[i+point_shift_1] - a4_Buffer[i+point_shift_2])* Multiplikator;

   } 
//----
//--- signal line counted in the 2-nd buffer

//     SimpleMAOnBuffer(rates_total,prev_calculated,0,InpSignalSMA,a5_Buffer,a6_Buffer);

//--- done

//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

Archivos adjuntos:

2018_01_10_Polynom_s4_s2_p72.mq4 15 kb

Evgeny Belyaev 2018.01.10 16:28 #1

¿Qué es el cálculo de diferencias?

Lo es:

Δf(xk) = f (xk+1) - f (xk)

Aleksey Panfilov 2018.01.10 16:33 #2

Aleksey Panfilov:

Propongo recopilar indicadores y expertos en cálculo de diferencias en esta rama, en código abierto.

He reescrito el indicador en una variante más clara como ejemplo:

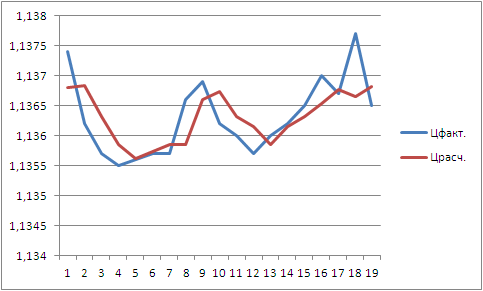
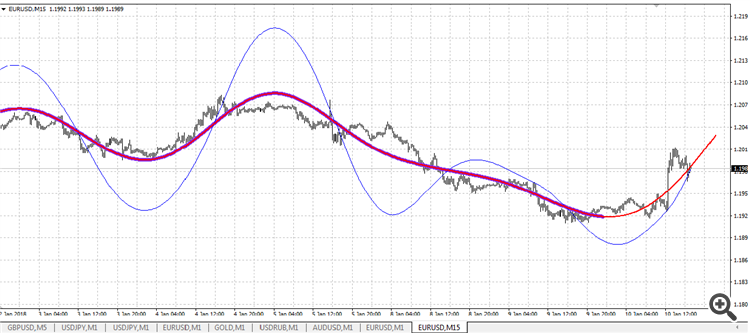
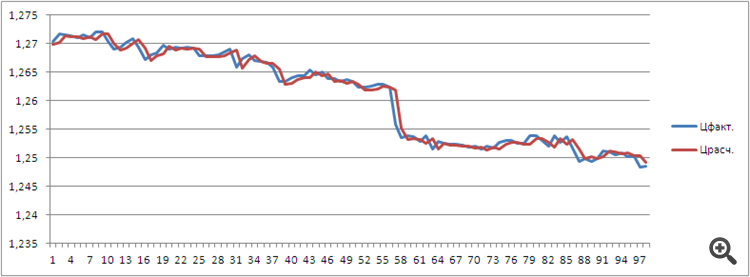
En el gráfico se ve así:

La línea azul-roja es la interpolación (encontrar un punto dentro del intervalo) mediante un polinomio de 4º grado con una palanca de 72.

      a1_Buffer[i]=((open[i] - Znach)    +5061600*a1_Buffer[i+1 ]-7489800   *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;

La línea azul delgada es la extrapolación (encontrar un punto fuera del intervalo) por el polinomio de grado 2 con palanca 78.

 a2_Buffer[i]=  3160*a1_Buffer[i]   -6240   *a1_Buffer[i+1 ]    +  3081*a1_Buffer[i+2 ];

La línea roja es la línea de construcción del polinomio de potencia 4. Se redibuja y se basa en el último punto de apertura de la barra.

 a4_Buffer[i+92]=a1_Buffer[i];   if(i<=10) { for(z=92-1;z>=0;z--){        a4_Buffer[i+0+z]=  5*a4_Buffer[i+1+z]  -  10*a4_Buffer[i+2+z]   +   10*a4_Buffer[i+3+z]  -  5*a4_Buffer[i+4+z]  +  1*a4_Buffer[i+5+z];  }}

Aleksey Panfilov 2018.01.10 16:34 #3

Evgeny Belyaev:

¿Qué es el cálculo de diferencias?

Lo es:

Δf(xk) = f (xk+1) - f (xk)

Sí.

Está directamente relacionado con el binomio de Newton.

Es cierto para los puntos equidistantes:

1*Y1-2*Y2+1*Y3=0 es la ecuación de diferencia de una recta.

1*Y1-3*Y2+3*Y3-1*Y4=0 - la ecuación en diferencia de la parábola de segundo grado.

1*Y1-4*Y2+6*Y3-4*Y4+ 1*Y5=0 - ecuación en diferencia de la parábola de tercer grado.

También se cruza con los temas:

https://www.mql5.com/ru/forum/61389/page48#comment_5633264

https://www.mql5.com/ru/forum/211220/page2#comment_5632736 .

Как измерить скорость цены

2017.07.20
www.mql5.com

Всем привет, тут такая тема Хочу использовать "ускорение" цены на тиковых интервалах, но не пойму как вообще посчитать скорость цены...

MetaEditor: editor profesional de Instrumentos de análisis fundamental Desarrollo de aplicaciones en

Evgeny Belyaev 2018.01.10 16:39 #4

Aleksey Panfilov:

Sí.

Eso es lo que todo el mundo ha estado haciendo... escribiendo...

¿Depende el futuro del pasado?

Aleksey Panfilov 2018.01.10 16:51 #5

Evgeny Belyaev:

Eso es lo que todo el mundo ha estado haciendo... escribiendo...

¿Depende el futuro del pasado?

Para cada acción, hay una huella en el presente, que por supuesto afecta al futuro. :))))

Sugiero que nos saltemos la filosofía en este hilo, y que hablemos sólo de matemáticas, programación, pruebas y optimización.

Instrumentos de análisis fundamental MetaTrader 5 para fórex, Simulador de estrategias comerciales

Yousufkhodja Sultonov 2018.01.10 16:53 #6

Aleksey Panfilov:

Sí.

Directamente relacionado con el binomio de Newton.

Para puntos equidistantes es cierto:

Y1-2*Y2+Y3=0 - ecuación de diferencia de una recta.

Y1-3*Y2+3*Y3-Y4 =0 - la ecuación de diferencia de la parábola de segundo grado.

Y1-4*Y2+6*Y3-4*Y4 + Y5 =0 - es la ecuación en diferencia de la parábola de tercer grado.

¿Has probado esta fórmula?

Y = a0 + a1X + a2X^2 + a3X^3 + a4X^4

donde:

X es el precio de la barra anterior;

Y - precio de la barra actual.

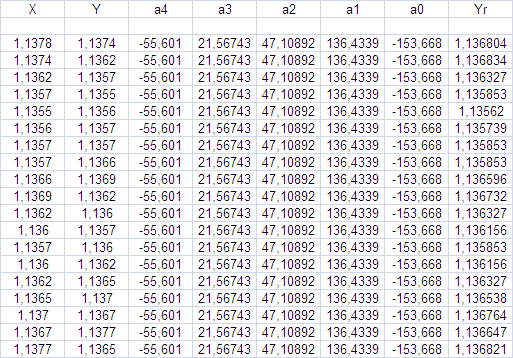
Y así obtenemos la siguiente imagen:

Aleksey Panfilov 2018.01.10 17:18 #7

Yousufkhodja Sultonov:

¿Has probado esta fórmula?

Y = a + bX + cX^2 + dX^3 + eX^4

Por supuesto, en esta forma hay X e Y, pero en la ecuación de recurrencia, sólo Y y todos los coeficientes (a + bX+ cX^2+ dX^3+ eX^4) se reducen y se sustituyen por cinco valores del propio Y.

Desarrollo de aplicaciones en MetaEditor: editor profesional de Robots comerciales e indicadores

Alexey Volchanskiy 2018.01.10 17:53 #8

He mirado el código, ¿he entendido bien, es alguna variante de un filtro de retroalimentación? ¿De dónde salen los coeficientes 5061600, 4926624 y otros?

En realidad, ¿de dónde salió el indie, de Internet? ))

Aleksey Panfilov 2018.01.10 18:07 #9

Alexey Volchanskiy:

1. He mirado el código, ¿he entendido bien, es alguna variante de un filtro de retroalimentación?

2.¿Y de dónde salen los coeficientes 5061600, 4926624 y otros?

3. En general, ¿de dónde viene el inductor, de internet? ))

1. Sí. Este filtro tiene 400 años de historia sólo escrita: Descartes, Newton, Pascal, Taylor, Lagrange.

2. Se calculan los coeficientes. Parece que en el segundo año, nos familiarizamos con los métodos de Lagrange y Taylor. Parece que hay muchas variantes para calcular los coeficientes.

3. Este en particular fue dibujado hoy. :)))))

Robots comerciales e indicadores Instrumentos de análisis fundamental Simulador de estrategias comerciales

Yousufkhodja Sultonov 2018.01.10 18:13 #10

Cuando se aumenta la muestra a N=100, la ecuación de 4º grado da el siguiente resultado:

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Nuevo comentario