
Self-optimization of EA: Evolutionary and genetic algorithms
Contents
- Introduction
- 1. How evolutionary algorithms first appeared
- 2. Evolutionary algorithms (methods)
- 3. Genetic algorithms (GA)
- 3.1. Field of application.
- 3.2. Problems being solved
- 3.3. Classic GA
- 3.4. Search strategies
- 3.5. Difference from the classic search of optimum
- 3.6. Terminology of GA
- 4. Advantages of GA
- 5. Disadvantages of GA
- 6. Experimental part
- 6.1. Search for the best combination of predictors
- with tabuSearch
- 6.2. Search for the best parameters of TS:
- 7. Ways and methods of improving qualitative characteristics
- Conclusion
Introduction
Many traders have long realized the necessity of a self-optimization that doesn't require the Expert Advisor to stop trading. There have been several related articles (article1, article2, article3, article4) published already. The experiments in these articles are based on the library suggested here. However, since they were published, new powerful optimization algorithms and new ways of applying them have emerged. In addition to that, I believe that these articles were written by programmers and were intended for programmers.
In this article, I will try to enlighten the practical application of genetic algorithms (GA) without going into depth with technical details, specifically aimed at traders. For users like me, it is important to know the principle of GA operation, the importance and value of parameters that affect quality and speed of GA convergence and its other utilitarian properties. Therefore, I may repeat myself, but, nevertheless, I will begin with the history of GA appearance, proceed with its description and get to identifying parameters of the improved GA. Also, we will compare GA with some evolutionary algorithms.
1. How evolutionary algorithms first appeared
The history of evolutionary calculations began with the development of various independent models. There were mainly genetic algorithms and Holland classification systems that were published in the early 60s and gained universal recognition after the book "Adaptation in Natural and Artifical Systems" was released in 1975, becoming a classic in its field. In the 70s, within the random search framework, L.A. Rastrigin introduced some algorithms that used ideas of bionic behavior. Development of these ideas found reflection in the series of work by I.L. Bukatova about evolutionary modeling. While developing ideas of M.L. Tsetlin about advisable and optimal behavior of stochastic machines, Y.I. Neumark suggested to search for global extremum based on the team of independent automata that models the processes of development and elimination of species. Fogel and Walsh are individuals that greatly contributed to the development of evolutionary programming. Despite their difference in approaches, each of these "schools" based their strategy on few principles that exist in nature and simplified them so they could be utilized on a computer.
Efforts focused on modeling evolution by analogy with systems of nature can be broken down into two major categories.
- Systems modeled based on biological principles. They have been successfully utilized for function optimization tasks, and can be easily described in non-biological language.
- Systems that appear more realistic from biological perspective, but are not particularly beneficial in the sense of application. They more resemble biological systems and are less directional (or not directional at all). They have a complicated and interesting behavior and, apparently, will shortly find practical use.
Certainly, we cannot divide these aspects so strictly in practice. These categories are in fact two poles where various computer systems lie between them. Closer to the first pole there are evolutionary algorithms like Evolutionary Programming, Genetic Algorithms and Evolution Strategies, for example. Closer to the second pole there are systems that can be classified as Artificial Life.
2. Evolutionary algorithms (methods)
Evolutionary algorithms — a division of artificial intelligence (section of evolutionary modeling), that uses and models the processes of natural selection. We list some of them:
- genetic algorithms — heuristic search algorithm used for optimization and modeling through random selection, combinations and variations of desired parameters;
genetic programming — automated creation or change of programs using genetic algorithms;
evolutionary programming — similar to genetic programing, but the program's structure is consistent, only numeric values are subject to change;
evolutionary strategies — resemble genetic algorithms, but only positive mutations are transmitted to the next generation;
differential evolution;
neuroevolution — similar to genetic programming, but genomes are artificial neural networks where evolution of weights at the specified network topology occurs, or besides evolution of weights topology evolution is also carried out.
They all model basic positions in theory of biological evolution — processes of selection, crossbreeding, mutation and reproduction. The behavior of species is determined by the environment. Multiple species are referred as population. Population evolves according to rules of selection in line with a target function set by the environment. This way, every specimen (individual) in population has its value in the environment assigned. Only the most suitable species are multiplied. Recombination and mutation allow individuals to change and adjust to the environment. Such algorithms refer to adaptive search mechanisms.
Evolutionary methods (EM) — approximate (heuristic) methods of solving tasks of optimization and structure synthesis. Majority of EM is based on static approach to researching situations and iterative approximation to the desired solution.
Evolutionary calculations constitute one of the sections of artificial intelligence. When creating artificial intelligence systems using this approach, the emphasis is made on building the initial model and rules based on which it can change (evolve). At the same time, the model can be created by applying various methods. For example, it can be either neural network or a set of logical rules. Annealing, genetic algorithms, PSO, ACO, and genetic programming relate to the main evolutionary methods.
Unlike precise methods of mathematical programming, evolutionary methods allow to find solutions close to optimal within reasonable time, and unlike other heuristic methods of optimization they are characterized by considerably smaller reliance on features of the application (i.e. more universal), and in the majority of cases provides a better degree of approximation to optimal solution. The universality of EM is also determined by applicability to tasks with non-metrizable space of managed variables (it means that there may be linguistic values, including those that have no quantifiable measure among managed variables).
In Simulated Annealing, the process of minimizing potential body energy during annealing of details is imitated. The change of some managed parameters takes place in the current point. A new point is always accepted when the target function improves and, with small probability, when it worsens.
The most important case of EM involves genetic methods and algorithms. Genetic algorithms (GA) are based on searching for the best solutions using inheritance and strengthening of useful features of multiple objects of a specific application in the process of imitation of their evolution.
Properties of objects are presented with values of parameters combined into a record that is called chromosome in EM. Subsets of chromosomes called population are operated in GA. Imitation of genetic principles — stochastic selection of parents among members of population, chromosomal crossover, selection of children to be included into new generation of objects based on evaluation of the target function. This process leads to evolutionary improvement of values of a target function (utility function) from generation to generation.
There are also methods among EM that unlike GA operate with a single chromosome instead of multiple chromosomes. This way, the discrete local search method called Hillclimbing is based on random change of separate parameters (values of fields in a record or, in other words values of genes in a chromosome). Such changes are called mutations. After every mutation, fitness function is evaluated. The result of mutation is saved in a chromosome only if fitness was improved. At the "annealing moduling", the mutation result is saved with a certain probability that depends on the obtained value.
In the Particles Swarm Optimization method, the behavior of multiple agents that aim to align their state with a state of the best agent is imitated.
The ACO method is based on imitation of ants behavior that shorten their routes from a source of food to their anthill.
3. Genetic algorithms (GA)
Genetic algorithms — adaptive search methods that have been commonly used for solving tasks of functional optimization lately. They are based on genetic processes of biological organisms: biological populations evolve during several generations and follow the rule of natural selection and the principal of survival of the fittest, as discovered by Charles Darwin. By imitating this process, genetic algorithms are capable of evolving solutions of real tasks, if they are coded appropriately.
In nature, species in population compete against one another for various resources, such as food and water. Furthermore, population members of the same type frequently compete for attracting a partner. Species that are more adjusted to the surroundings have better chances to create offspring. Inferior species either don't reproduce, or they have only a few offspring. It means that genes of well adapted species will spread with growing number of descendants in every new generation. A combination of successful characteristics from different parents can sometimes lead to "overly adapted" descendant who is more adaptable than any of his parents. This way, a kind develops and adjusts to the environment even better.
Genetic algorithms draw an analogy with this mechanism. They operate with a set of "species" — population, where each of them provides a possible solution of a problem. Each specimen is evaluated with a measure of "adjustment" in accordance to how "good" a relevant solution is. The fittest species obtain the opportunity to "create" offspring using "crossbreeding" with other population species. This leads to the appearance of new species that combine some characteristics inherited from their parents. The least fit species are less likely to create children, so the characteristics that they possess will gradually disappear from population in the process of evolution.
This is how the entire new population of acceptable solutions is reproduced by selecting the best representatives of a previous generation, crossbreeding them and obtaining new species. This new generation contains a higher proportion of characteristics that "good" members of a previous generation posses. This way, good characteristics are distributed across all population from generation to generation. Crossbreeding the fittest species leads to the most perspective areas of search space being explored. Ultimately, the population will come down to the optimal solution.
There are different ways of implementing ideas of biological evolution within GA.
3.1. Field of application
The real tasks solved can be identified as a search of optimal value, where value is a complicated function that depends on several input parameters. In some cases, it is of interest to find values of parameters that are used to achieve the most accurate function value. In other cases, accurate optimum is not required, and any value that is better than a set value can be considered as a solution. In this case, genetic algorithms frequently become the most appropriate method for searching for "good" values. The force of a genetic algorithm is in its ability to simultaneously manipulate with multiple parameters. This feature of GA was used in hundreds of applications, including the designing of aircrafts, setting parameters of algorithms and searching for stable conditions of systems of nonlinear differential equations.
However, there are cases when GA doesn't operate as efficiently as expected.
Let's assume that there is a real task that involves searching for the optimal decision. How to find out if it is suitable for GA? There has been no strict answer to this question until now. However, many researchers share the assumption that GA has good chances to become an efficient search procedure in the following cases:
- if the search field to be researched is big, and it is assumed that it is not completely smooth and unimodal (i.e. contains one smooth extremum);
- if fitness function contains noise;
- or if a task doesn't require a strict finding of global optimum.
In other words, in situations when it is required to find the acceptable "good" solution (which is rather common with real tasks), GA competes and beats other methods that don't apply knowledge of the search area.
If the search area is small, then solution can be found using the exhaustive search, and you can rest assured that the best possible solution is found, whereas GA would most likely to converge on a local optimum, rather than an overall better solution. If the space is smooth and unimodal, then any gradient algorithm (for example, the steepest descent method) will be more effective than GA.
If there is some additional information about the search area (for example, the area for a well known "traveling salesman problem"), search methods that use heuristics determined by area, frequently outperform any universal method that GA is. Considering a relatively complicated structure of the fitness function, search methods with a single solution at the moment of time, such as a simple method of descent, could "get caught in" a local solution. However, it is considered that genetic algorithms have less chances to converge on a local optimum and safely function on a multi-extremal landscape, since they operate with the entire "population" of solutions.
Certainly, such assumptions don't strictly predict when GA will be an efficient search procedure competing with other procedures. The efficiency of GA highly depends on details like method of coding solutions, operators, setting parameters, partial criterion of success. Theoretical work that is documented in literature on genetic algorithms so far doesn't give grounds for discussing the development of strict mechanisms for accurate predictions.
3.2. Problems being solved
Genetic algorithms are applied for solving the following tasks:- Optimizing functions
- Optimizing requests in data bases
- Various tasks on the charts (traveling salesman problem, coloring, finding pairs)
- Setting and training artificial neural networks
- Layout tasks
- Creating schedules
- Game strategies
- Approximation theory
3.3. Classic GA
Operation of simple GAThe simple GA randomly generates the initial population of structures. GA operation is an iteration process that carries on until the set number of generations is achieved or any other termination criteria is applied. The selection proportional to fitness, a single-pointed crossover and mutation are implemented in every generation of the algorithm.
First, proportional selection appoints to every structure the Ps(i) probability that equals ratio of its fitness to the total fitness of population.
Then all n species are selected (with replacement) for further genetic data handling according to the Ps(i) value. The simplest proportional selection is a roulette-wheel selection, Goldberg, 1989c) — species are selected with n "spins" of a roulette. The roulette wheel contains one sector for each member of population. The size of i-th sector is proportional to the corresponding value Ps(i). At this selection, the fittest members of population are more likely to be selected than the least fit species.
After selection, n selected species are subject to crossover (sometimes called recombination) with a set probability of Pc. n strings are randomly divided into n/2 pairs. For every pair with Pc probability, crossover can be applied. Accordingly, the crossover doesn't occur with 1-Pc probability, and constant species proceed to the mutation stage. If there is a crossover, then the obtained children replace their parents and proceed to mutation.
A one-point crossover operates as follows. First, one out of l-1 break points is randomly selected. (Break point is an area between adjacent bytes in a string.) Both parent structures are divided into two segments based on this point. Then, corresponding segments of different parents are linked, and two genotypes of children are created.
After the crossover stage ends, mutation operators are performed. Every byte with the Pm probability is changed to the opposite in every string that is subject to mutation. The population obtained after mutation overwrites the old population, and this is how a loop of one generation is ended. The following generations are handled the same way: selection, crossover and mutation.
Researches of GA currently offer plenty of other operators of selection, crossover and mutation. Below are the most common ones. First of all, tournament selection (Brindle, 1981; Goldberg и Deb, 1991). It implements n tournaments to select n species. Every tournament is built on the selection of k elements from the population and the selection of the best specimen amongst all. The tournament selection with k=2 is the most common.
Elite selection methods (De Jong, 1975) guarantee that the best members of population will survive during selection. The most common process is a compulsory retention of a single best specimen, if it didn't go through the process of selection, crossover and mutation like the rest. Elitism can be integrated in almost any standard method of selection.
Two-point crossover (Cavicchio, 1970; Goldberg, 1989c) and a uniform crossover (Syswerda, 1989) — are decent alternatives to the one-point operator. There are two break points selected in the two-point crossover, and parent chromosomes exchange a segment that is between these two points. In a uniform crossover, every byte of the first parent is inherited with the first child with a set probability, otherwise, this byte in transferred to the second child. And vice versa.
Basic operators of genetic algorithm
Selection operator
At this stage, the optimal population is selected for further reproduction. The specific number of the fittest is normally taken. It makes sense to drop "clones", i.e. species with the same set of genes.
Crossbreeding operator
Most often, crossbreeding is performed over the best two species. The usual results are two species with components taken from their "parents". The goal of this operator is to distribute "good" genes across population and to tighten the density of population towards areas where it is high already.
Mutation operation
Mutation operator simply changes the arbitrary number of elements in a specimen to other arbitrary numbers. In fact, it is a dissipative element that pulls from local extremums on the one hand, and adds new information to population on the other hand.
- In case of a binary sign, it inverts a byte.
- It changes the numerical sign to a certain value (most probably, the closest value).
- It replaces to other nominal sign.
Stop criteria
- Finding global or suboptimal solution
- Exit to "plateus"
- Exhausting the number of generations released for evolution
- Exhausting the time remaining for evolution
- Exhausting the specified number of calls to the target function
3.4. Search strategies
The search is one of universal ways of finding solutions for cases when the sequence of steps leading to optimum is not known.There are two search strategies: exploitation of the best solution and studying the space of solutions. A gradient method is an example of a strategy that selects the best solution for a possible improvement, by ignoring the research of the entire search area. A random search is an example of a strategy that, on the contrary, studies the area of solutions while ignoring researches of perspective fields of the search area. A genetic algorithm is a class of search methods of a general function that combine elements of both strategies. Applying these methods enables to keep the acceptable balance between research and exploitation of the best solution. At the start of genetic algorithm's operation, population is random and has diverse elements. Therefore, crossbreading operator conducts a vast research of solution area. With increase of fitness function of obtained solutions, the cross-breeding operator enables researching each of their surroundings. In other words, the type of search strategy (exploitation of the best solution or researching the solution area) for crossbreeding operator is defined with a population diversity, instead of the operator itself.
3.5. Difference from the classic search of optimum
Generally, the algorithm of solving optimization problems is a sequence of calculation steps that asymptotically converge on the optimal solution. The majority of classic optimization methods generate a determined sequence of calculations that is based on a gradient or a derivative of a target function of a higher range. These methods are applied to a single output point of a search area. Then the decision is gradually improved towards the fastest increase or decrease of the target function. With such detailed approach, there is a risk of hitting the local optimum.
A genetic algorithm performs a simultaneous search in various directions through using population of possible solutions. Switching from one population to another avoids hitting the local optimum. Population undergoes something similar to evolution: relatively good solutions are reproduced in every generation, whereas relatively bad ones die out. Genetic algorithms use probability rules to identify a reproduced or a destroyed chromosome in order to direct the search to areas of a possible improvement of the target function.
Many genetic algorithms were implemented in recent years, and in the majority of cases they drastically differ from the initial classic algorithm. And this is the reason why instead of one model, there is a wide range of algorithm classes that bear little resemblance with each other under the term "genetic algorithms". Researchers experimented with various types of views, crossover operators and mutations, special operators and various approaches to reproduction and selection.
Although the model of evolutionary development applied in GA is majorly simplified in comparison with it nature analog, nevertheless, GA is a powerful tool and can be successfully applied for a wide class of tasks, including those that are difficult and sometimes impossible to solve using other methods. However, GA along with other methods of evolutionary calculations, can't guarantee finding a global solution over polynomial time. Neither can be guaranteed that global solution will be even found. However, genetic algorithms are good for searching for "relatively good" solution "relatively fast". Almost always these methods will be more effective than GA in both speed and accuracy of found solutions, where special methods can be used to find a solution. The main advantage of GAs is that they can be applied even for complicated tasks, if there are no special methods. Even where existing methods work well, GAs can be used for further improvement.
3.6. Terminology of GA
Since GA derives from natural science (genetics) and computer science, the applied terminology is a mixture of natural and artificial compounds. Terms referring to GA and the solution of optimization problems are provided in table. 1.1.
Table 1.
| Genetic algorithm | Explanation |
|---|---|
| Chromosome | Possible solution (set of parameters) |
| Genes | Parameters that are optimized |
| Locus (location) | Position of a gene in a chromosome |
| Allele | Value of gene |
| Phenotype | Uncoded solution |
| Genotype | Coded solution |
Classic (one-point) crossing over.
"Traditional" genetic algorithm uses a one-point crossing over where two chromosomes are cut once in a specific point, and the obtained parts are exchanged afterwards. Other various algorithms with other types of crossing over frequently including more than one cut point were also discovered. DeJong had researched the efficiency of a multi-pointed crossing over and came to conclusion that a two-point crossing over shows improvement, but further adding of crossing over points reduces the activity of a genetic algorithm. The problem of adding additional crossing over points is that standard blocks will most probably be interrupted. However, the advantage of multiple crossing over points is that the area of states can be researched in more details.
Two-point crossing over.
In two-point crossing over (and multiple point crossing over generally) chromosomes are considered as loops formed when connecting the ends of linear chromosomes together. In order to change a segment of one cycle to a segment of another cycle, a selection of two cut points is required. In this presentation, a one-point crossing over can be considered as a crossover with two points, but with one cut point fixed at the beginning of the string. Therefore, a two-point crossing over solves the same task as a one-point crossover, but in a more complete way. A chromosome considered as a cycle may contain a lot of standard blocks, because they can perform a "cyclic return" at the end of the string. Many researchers currently agree that, in general, two-point crossover is better than a one-point crossover.
Unified (homogeneous) crossing over.
Unified crossing over is fundamentally different from a one-point crossover. Every gene in a generation is created by copying a relevant gene from one parent or another that was selected according to randomly generated crossover mask. If a crossover mask has 1, then a gene is copied from a first parent, if it has 0, then a gene is copied from a second parent. In order to create a second generation the process is repeated, but on the contrary, with exchanged parents. A new crossover mask is randomly generated for each pair of parents.
Differential crossing.
Apart from the crossover, there are other methods of crossbreeding. For example, for searching a minimum/maximum function of many physical variables, "differential crossbreeding" is the most successful. We will briefly describe its concept. Let's imagine that a and b are two individuals in a population, i.e. physical vectors that our function depends on. Then a child (c) is calculated using the formula с=a+k*(a-b), where k — is a certain physical ratio (that can depend on ||a-b|| — a distance between vectors).
Mutation in this model is an addition to an individual of a random short length vector. If an output function is continuous, then a model operates well. It is even better if it is smooth.
Inversion and reordering.
The order of genes in a chromosome is often critical for building blocks that allow to perform an efficient operation of the algorithm. During the algorithm operation, methods for reordering positions of genes in a chromosome were suggested. One of such methods is inversion that reverses the order of genes between two randomly selected positions in a chromosome. (When these methods are used, genes need to have a certain "mark", so they could be correctly identified despite of their position in a chromosome.)
The goal of reordering is to attempt finding the order of genes that hold the best evolutionary potential. Many researchers have applied inversion in their work, although it seems that only few have tried to justify it or evaluate its contribution. Goldberg & Bridges analyze the operator of reordering on a very small task, showing that it can give a certain advantage, however, they conclude that their methods wouldn't have the same advantage with big tasks.
Reordering also considerably increases the search area. Not only a genetic algorithm attempts to find good sets of values of genes, at the same time it also tries to find their "right" order. This is a bigger challenge to solve.
What is epistasis?
The "epistasis" term in genetics is determined as influence of a gene on an individual's fitness depending on value of a gene present in other place. In other words, geneticists use the term "epistasis" in terms of a "switch" or "masking" effect: "A gene is considered epistatic when its presence suppresses the influence of a gene in other locus. Epistatic genes are sometimes called inhibitory because of their influence on other genes that are described as hypostasis.
In the GA terminology it may sound like: "Fitness of a specimen depends on a position of chromosomes in a genotype".
What is a false optimum?
One of fundamental principles of genetic algorithms is that chromosomes included in templates contained in global optimum are increased in frequency. This is especially right for short templates of small order, known as building blocks. Ultimately, these optimal templates will meet at the crossover, and a global optimal chromosome will be created. But if templates that are not contained in a global optimum will be increased by frequency quicker than others, then a genetic algorithm will be misled and will deviate from the global optimum, instead of approaching it. This phenomenon is known as false optimum.
False optimum is a particular case of epistasis, and it was deeply analyzed by Goldberg and others. False optimum is directly linked with negative impact of epistasis in genetic algorithms.
Statistically, the template will increase by frequency in population, if its fitness is higher than the average fitness of all templates in a population. The task is marked as a false optimum task, if the average fitness of templates that are not contained in a global optimum is more than the average fitness of other templates.False optimum tasks are complex. However, Grefenstette wittily demonstrates that there are not always complications. After the first generation, a genetic algorithm doesn't obtain an objective selection of points in the search area. Therefore it cannot objectively evaluate a global average fitness of a template. It is only capable of obtaining a biased evaluation of a template fitness. Sometimes this bias help a genetic algorithm to match (even if a task could otherwise have a stronger false optimum).
What is inbreeding, outbreeding, selective choice, panmixia?
There are several approaches to selecting a parent pair. The simplest out of all of them is panmixia. This approach implies a random selection of a parent pair when both species that make a pair are randomly selected from the entire population. In this case, any specipem can become a member of several pairs. Despite the simplicity, this approach is universal for solving various tasks. However, it is relatively critical to a population number, since the algorithm efficiency that implements this approach is decreased with an increase of population.
With a selective method of choosing species for a parent pair, only those species whose fitness is above the average fitness in a population can become "parents", at equal probability of such candidates to make a pair.
This approach enables a quicker convergence of the algorithm. However, due to a quick convergence, a selective choice of a parent pair is not suitable when few extremums must be defined, because the algorithm quickly comes down to one of solutions with such tasks. Furthermore, for few classes of tasks with a complicated landscape of fitness, quick convergence can turn into a premature convergence to a quasi-optimal solution. This disadvantage can be partially compensated with a use of a suitable selection mechanism that would "slow down" overly fast convergence of an algorithm.
Inbreeding is a method when the first member of a pair is random, and the second specimen is selected to be as close as possible to the first member.
The concept of similarity of species is also applied for outbreeding. Now, however, pairs are formed from species that are as far as possible.
The last two methods differently influence the behavior of a genetic algorithm. Thus, inbreeding can be characterized with a property of concentrating the search in local nodes, that, in fact, leads to dividing a population into separate local groups around extremum suspicious areas of landscape. Outbreeding is aimed at preventing the algorithm convergence to already found solutions by forcing the algorithm to search through new areas that remain to be explored.
Dynamic self-organization of GA parameters
Frequently, the selection of parameters of a genetic algorithm and specific genetic operators is performed using intuition, since there is no objective evidence that some settings and operators are more advantageous. However, we shouldn't forget that the point of GA is in dynamics, the algorithm "softness" and calculations performed. Then why not to let the algorithm to configure itself to the time of solving a task and adapt to it?
The easiest way is to organize the adaption of applied operators. For this purpose, we will build few (the more the better) various operators of selection (elite, random, roulette,..), crossing over (one-point, two-point, unified,..) and mutation (random one-element, absolute,..) into the algorithm. Let's set equal probabilities of application for each operator. On every loop of the algorithm, we will select one operator for each group (choice, crossing over, mutation) in accordance with possible distribution. We will mark in the obtained specimen from which operator it was received. Then, if a new distribution of probabilities will be calculated based on information contained in population (probability of applying the operator is proportional to a number of species in a population obtained with this operator), then a genetic algorithm will receive a mechanism of a dynamic self-adaptation.
This approach provides yet another advantage: now, there is no need to worry about the applied generator of random figures (linear, exponential, etc.), since the algorithm dynamically changes the distribution mode.
Migration and artificial selection method
Unlike regular GA, macro evolution is performed, i.e. not just one, but several populations are created. A genetic search here is performed by uniting parents from various populations.
Interrupted balance method
A method is based on paleontological theory of interrupted balance that describes a quick evolution through volcanic and other changes of the earth's crust. In order to apply this method in technical tasks, it is advised to randomly shuffle individuals in a population after every generation, and then form new current generations. As with wildlife, unconscious selection of parent pairs and a synthetic selection of parent pairs can be suggested here. Then, results of both selections should be randomly mixed, and instead of keeping the size of population constant, it should be managed depending on presence of best individuals. Such modification of the interrupted balance methods may reduce unsound populations and increase populations with the best species.
Interrupted balance method is a powerful stress method for changing the environment that is used for efficient exit from local pits.
4. Advantages of GA
There are two main advantages of genetic algorithms over classic optimization methods.
1. GA has no considerable mathematic requirements to types of target functions and restrictions. A researcher shouldn't simplify the model's object by loosing it adequacy and artificially ensuring the application of available mathematic methods. The most diverse target functions and restriction types (linear and non-linear) that are defined on discrete, uninterrupted, and mixed universal sets can be used.
2. When using classic step-by-step methods, the global optimum can be found only when a problem has a convexity property. At the same time, evolutionary operations of genetic algorithms allow searching for global optimum efficiently.
Least serious but still important advantages of GA:
a large number of free parameters that allow building heuristics efficiently;
efficient parallelization;
works as good as a random search;
connection with biology gives some hope for exceptional efficiency of GA.
5. Disadvantages of GA
Multiple free parameters that turn "operation with GA" to the "game with GA"
Lack of evidentiary support for convergence
In simple target functions (smooth, one extrema and etc.), genetics always loose in speed to simple search algorithms
6. Experimental part
All experiments will be performed in the R 3.2.4 language environment. We use a set of data for training a model and majority of functions from the previous article.
The CRAN depositary section that contains a large number of dedicated packages aimed for optimization and mathematic programming tasks. We will apply several various methods of GA and EM for solving the above mentioned tasks. There is only one requirement to models that participate in the process of optimization — speed. It isn't advisable to apply methods that are trained within hundred seconds. In consideration that in every generation there will be a minimum of 100 species, and population will pass through several (from unity to dozens) epochs, the optimization process will stretch over unacceptable time. In the previous articles we applied two types of deep networks (with SAE and RBM initialization). Both have showed high speed and may well be used for genetic optimization.
We are going to solve two optimization tasks: search of the best combination of predictors and the selection of optimal parameters of indicators. We will apply the XGBoost(Extreme Gradient Boosting) algorithm that is often used to solve the first task (predictor selection) in order to learn new algorithms. As mentioned in sources, it shows very good results in classification tasks. The algorithm is available for R, Python, Java languages. In the R language, this algorithm is implemented in the “xgboost” v package. 0.4-3.
In order to solve the second task (selection of optimal parameters of indicators), we will use the simplest Expert Advisor MACDsample , and see what can be obtained with its help when using genetic optimization on the flow.
6.1. Search for the best combination of predictors
It is important to define the following for solving the optimization task:
parameters that will be optimized;
optimization criterion — scalar that needs to be maximized/minimized. There can be more than one criterion;
target (objective, fitness) function that will calculate the value of optimization criterion.
A fitness function in our case will consistently implement the following:
forming the initial data frame;
dividing it into train/test;
training the model;
testing the model;
calculating optimization criterion.
The optimization criterion can be standard metrics like Accuracy, Recall, Kappa, AUC, as well as the ones provided by a developer. We will use a classification error in this capacity.
The search of the best combination of predictors will be performed with the "tabuSearch" v.1.1 package that is an extension to the HillClimbing algorithm. The TabuSearch algorithm optimizes a binary string by using an objective function identified by a user. As a result, it gives out the best binary configuration with the highest value of objective function. We will use this algorithm for searching for the best combination of the predictor.
The main function:
tabuSearch(size = 10, iters = 100, objFunc = NULL, config = NULL, neigh = size, listSize = 9, nRestarts = 10, repeatAll = 1, verbose = FALSE)
Arguments:
size – length of the optimized binary configuration;
iters – number of iterations in preliminary algorithm search;
objFun – a method suggested by a user that evaluates a target function for a specified binary string;
config – starting configuration;
neigh – number of adjacent configurations for checking on every iteration. By default, it equals the length of the binary string. If a number is less than the string length, neighbors are randomly selected;
listSize – size of taboo list;
nRestarts – maximum times of restarting at the intensive stage of algorithm search;
repeatAll – number of search repetitions;
verbose – logical if true, the name of the current algorithm stage is printed, for example, a preliminary stage, intensification stage, diversification stage.
We will write an objective function and proceed to experimenting.
ObjFun <- function(th){
require(xgboost)
# Exit if all zero in binary string
if (sum(th) == 0) return(0)
# names of predictors that correspond to 1 in the binary string
sub <- subset[th != 0]
# Create structure for training a model
dtrain <- xgb.DMatrix(data = x.train[ ,sub], label = y.train)
# Train a model
bst = xgb.train(params = par, data = dtrain, nrounds = nround, verbose = 0)
# Calculate forecasts with the text set
pred <- predict(bst, x.test[ ,sub])
# Calculate forecast error
err <- mean(as.numeric(pred > 0.5) != y.test)
# Return quality criterion
return(1 - err)
}
For calculations we should prepare data sets for training and testing the model, and also to define the model's parameters and the initial configuration for optimization. We use the same data and functions as from the previous article (EURUSD/M30, 6000 bars as at 14.02.16).
Listing with comments:
#---tabuSearch---------------------- require(tabuSearch) require(magrittr) require(xgboost) # Output dataframe dt <- form.data(n = 34, z = 50, len = 0) # Names of all predictors in the initial set subset <- colnames(In()) set.seed(54321, kind = "L'Ecuyer-CMRG") # Prepare sets for training and testing DT <- prepareTrain(x = dt[ ,subset], y = dt$y, balance = FALSE, rati = 4/5, mod = "stratified", norm = FALSE, meth = method) train <- DT$train test <- DT$test x.train <- train[ ,subset] %>% as.matrix() y.train <- train$y %>% as.numeric() %>% subtract(1) x.test <- test[ ,subset] %>% as.matrix() y.test <- test$y %>% as.numeric() %>% subtract(1) # Initial binary vector th <- rep(1,length(subset)) # Model parameters par <- list(max.depth = 3, eta = 1, silent = 0, nthread = 2, objective = 'binary:logistic') nround = 10 # Initial configuration conf <- matrix(1,1,17) res <- tabuSearch(size = 17, iters = 10, objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1) # Maximum value of objective function max.obj <- max(res$eUtilityKeep) # The best combination of the binary vector best.comb <- which.max(res$eUtilityKeep)%>% res$configKeep[., ] # The best set of predictors best.subset <- subset[best.comb != 0]
We start optimization with ten iterations and see what is the maximum quality criterion and predictor set.
> system.time(res <- tabuSearch(size = 17, iters = 10, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) user system elapsed 36.55 4.41 23.77 > max.obj [1] 0.8 > best.subset [1] "DX" "ADX" "oscDX" "ar" "tr" "atr" [7] "chv" "cmo" "vsig" "rsi" "slowD" "oscK" [13] "signal" "oscKST" > summary(res) Tabu Settings Type = binary configuration No of algorithm repeats = 1 No of iterations at each prelim search = 10 Total no of iterations = 30 No of unique best configurations = 23 Tabu list size = 9 Configuration length = 17 No of neighbours visited at each iteration = 17 Results: Highest value of objective fn = 0.79662 Occurs # of times = 2 Optimum number of variables = c(14, 14)
The calculations took approximately 37 seconds with prediction accuracy of around 0.8 and 14 predictors. The obtained quality indicator with default settings is very good. Let's do another calculation, but with 100 iterations.
> system.time(res <- tabuSearch(size = 17, iters = 100, + objFunc = ObjFun, config = conf, listSize = 9, nRestarts = 1)) user system elapsed 377.28 42.52 246.34 > max.obj [1] 0.8042194 > best.subset [1] "DX" "ar" "atr" "cci" "chv" "cmo" [7] "sign" "vsig" "slowD" "oscK" "SMI" "signal" >
We see that the increase of iterations has proportionally increased the calculation time, unlike the forecast precision. It has increased only slightly. It means that quality indicators must be improved through setting the model's parameters.
This is not the only algorithm and package that helps to select the best set of predictors using GA. You can use the kofnGA, fSelector packages. Apart from those, a selection of predictors is implemented by gafs() function in the "caret" package using GA.
6.2. Searching for the best parameters of ТС
1. Output data for projecting. We will use the MACDSampl Expert Advisor as an example.
In the MACDSample Expert Advisor, an algorithm generating signals when crossing the macd and signal strings is implemented. One indicator is used.
MACD(x, nFast = 12, nSlow = 26, nSig = 9, maType, percent = TRUE, ...)Arguments
|
x |
Timeseries of one variable; normally is price, but can be volume, and etc. |
|
nFast |
Number of periods for quick MA. |
|
nSlow |
Number of periods for slow MA |
|
nSig |
Number of periods for signal MA |
MaType – type of applied MA
percent – logical if true, then the difference between fast and slow MA in percentage is returned, otherwise — simple difference.
The MACD function returns two variables: macd — difference between fast MA and slow МА, or speed of distance change between fast МА and slow МА; signal — МА from this difference. MACD is a particular case of a common oscillator applied to the price. It can be also used with any timeseries of one variable. Time periods for MACD are frequently set as 26 and 12, but the function has initially used exponential constants 0.075 and 0.15 that are closer to 25.6667 and 12.3333 periods.
So, our function has 7 parameters with a range of change:
p1 — calculated price (Close, Med, Typ, WClose)
p2 — nFast (8:21)
p3 — nSlow(13:54)
p4 — nSig (3:13)
p5 — MAtypeMACD – МА type for the MACD string
p6 — MatypeSig – МА type for the Signal string
p7 — percent (TRUE, FALSE)
p5,p6 = Cs(SMA, EMA, DEMA, ZLEMA).
Trading signals can be generated in different ways:
Option 1
Buy = macd > signal
Sell = macd < signal
Option 2
Buy = diff(macd) > 0
Sell = diff(macd) <= 0
Option 3
Buy = diff(macd) > 0 & macd > 0
Sell = diff(macd) < 0 & macd < 0
This is another optimization parameter signal(1:3).
And, finally, the last parameter — depth of history of optimization len = 300:1000 (the number of last bars where optimization is held).
In total we have 9 parameters of optimization. I have increased their number on purpose in order to show that anything can be used as a parameter (figures, strings and etc.).
The optimization criterion — К quality ratio in points (in my previous publications it was already thoroughly described).
For optimizing parameters we need to identify a fitness (objective) function that will calculate the quality criterion and select the optimization program. Let's start with the program.
We will apply secure, fast and, most importantly, repeatedly tested "rgenoud" package. Its main restriction implies all parameters to be either all integer or physical. This is a mild restriction, and it is gently bypassed. The genoud() function combines the evolutionary search algorithm with methods on the basis of derivative (Newton or quasi-Newton)for solving various optimization problems. Genoud() can be used for solving optimization problems for which derivatives are not defined. Furthermore, using the cluster option, the function supports the use of several computers, processors and cores for a qualitative parallel calculation.
genoud(fn, nvars, max = FALSE, pop.size = 1000, max.generations = 100, wait.generations = 10, hard.generation.limit = TRUE, starting.values = NULL, MemoryMatrix = TRUE, Domains = NULL, default.domains = 10, solution.tolerance = 0.001, gr = NULL, boundary.enforcement = 0, lexical = FALSE, gradient.check = TRUE, BFGS = TRUE, data.type.int = FALSE, hessian = FALSE, unif.seed = 812821, int.seed = 53058, print.level = 2, share.type = 0, instance.number = 0, output.path = "stdout", output.append = FALSE, project.path = NULL, P1 = 50, P2 = 50, P3 = 50, P4 = 50, P5 = 50, P6 = 50, P7 = 50, P8 = 50, P9 = 0, P9mix = NULL, BFGSburnin = 0, BFGSfn = NULL, BFGShelp = NULL, control = list(), optim.method = ifelse(boundary.enforcement < 2, "BFGS", "L-BFGS-B"), transform = FALSE, debug = FALSE, cluster = FALSE, balance = FALSE, ...)
Arguments
- fn – objective function that is minimized (or maximized if max = TRUE). The first argument of the function must be a vector with parameters that are used for minimizing. The function should return the scalar (except when lexical = TRUE)
- nvars – quantity of parameters that will be selected for a minimized function
- max = FALSE maximize (TRUE) or minimize (FALSE) the objective function
- pop.size = 1000 size of population. This is a number of species that will be used for solving optimization problems. There are few restrictions regarding the value of this figure. Despite that the number of population is requested from a user, the figure is automatically corrected in order to satisfy relevant restrictions. These restrictions derive from the requirements of some GA operators. In particular, the Р6 operator (simple crossover) and Р8 (heuristic crossover) require the number of species to be even, i.e. they request both parents. Therefore, the pop.size variable must be even. If not, then population is increased to satisfy these restrictions.
- max.generations = 100 — maximum generations. This is a maximum number of generations that genoud will perform at the attempt to optimize the function. This is a mild restriction. Maximum generations will act for genoud, only if hard.generation.limit will be set in TRUE, otherwise two soft triggers will control when genoud must stop: wait.generations and gradient.check.
Despite that the max.generations variable doesn't restrict the number of generations by default, it is nevertheless important because many operators use it to correct their behavior. In fact, many operators become less random, since the number of generations becomes closer to the max.generations limit. If the limit is exceeded and genoud decides to proceed with operation it automatically increases the max.generation limit.
- wait.generations = 10. If the target function doesn't improve in this number of generations, then genoud will think that the optimum is found. If the gradient.check trigger was enabled, then genoud will start calculating wait.generations only if gradients within solution.tolerance will equal zero. Other variables that manage the completion are max.generations and hard.generation.limit.
- hard.generation.limit = TRUE. This logical variable determines if the max.generations variable is a compulsory restriction for genoud. When hard.generation.limit is displayed on FALSE, genoud can exceed the quantity of max.generations, if the target function was improved in any number of generations (determined in wait.generations), or if the gradient (determined in gradient.check) doesn't equal zero.
- starting.values = NULL — vector or matrix that contains values of parameters that genoud will use at the start. By using this option, a user can enter one or more species into the starting population. If a matrix is provided, then columns must be parameters and strings — species. genoud will create other species in a random order.
- Domains = NULL . This is nvars *2 matrix. For every parameter in the first column — lower boarder, second column — upper boarder. No species from thegenoud starting population won't be generated beyond boundaries. But some operators can generate subsidiary elements that will be positioned beyond the boarders, if the boundary.enforcement flag will not be enabled.
- If a user fails to provide values for domains, then genoud will set domains by default through default.domains.
- default.domains = 10. If a user doesn't want to provide a matrix of domains, then, nevertheless, domains can be set by a user with this easy to use scalar option. Genoud will create the domain matrix by setting a lower boarder for all parameters that equals (-1 )* default.domains, and an upper boarder that equals default.domains.
- solution.tolerance = 0.001. This is a security level used in genoud. Figures with solution.tolerance difference, as suggested, are equal. This is particularly important when it reaches the evaluation of wait.generations and performing gradient.check.
- gr = NULL. Function that provides a gradient for BFGS optimizer. If it is NULL, then numerical gradients will be used instead.
- boundary.enforcement = 0. This variable determines the level until which genoud is subject to boundary restrictions of the search area. Despite the value of this variable, none of the species from the starting generation will have the values of parameters beyond the boundaries of the search area.
boundary.enforcement has three possible values: 0 (all suitable), 1 (partial restriction), and 2 (no violations of boundaries):
0: all suitable, this option allows any operator to create species beyond the search area. These species will be included in a population, if their fitness values are sufficiently good. Boarders are important only when generating random species.
1: partial restriction. This allows operators (especially those who use the optimizer based on a derivative, BFGS), to go beyond the boundaries of the search area during the creation of a specimen. But when an operator selects a specimen, it must be within reasonable boundaries.
2: no violation of boundaries. Beyond the search area, evaluations will never be required. In this case, the restriction of boundaries is also applied to the BFGS algorithm that prevents candidates from deviation beyond boundaries determined by Domains. Please pay attention that it causes the use of the L-BFGS-B algorithm for the optimization. This algorithm requires that all suitable values and gradients are determined and final for all functional evaluations. If this causes error, it is advised to use BFGS algorithm and the boundary.enforcement=1 setting.
- lexical = FALSE. This option includes lexical optimization. This is an optimization by several criteria, and they are determined sequentially in the order given by the fitness function.The fitness function used with this option must return the numerical vector of fitness values in the lexical order. This option can have FALSE, TRUE or integer values that equal the number of suitable criteria returned by the fitness function.
- gradient.check = TRUE. If this variable equals TRUE, then genoud won't start counting wait.generations, until every gradient won't be close to zero with solution.tolerance. This variable has not effect if the limit of max.generations was exceeded, and hard.generation.limit option was set in TRUE. If BFGSburnin < 0, then this will be ignored, if gradient.check = TRUE.
- BFGS = TRUE. This variable questions if Quasi-Newton derivative optimizer (BFGS) should be applied towards the best specimen at the end of every generation after the initial one. Setting in FALSE doesn't mean that BFGS won't be applied. In particular, if you wish that BFGS is never applied, the Р9 operator (local minimum crossover) must be reset.
- data.type.int = FALSE. This option sets the data type of parameters of the optimized function. If the variable is TRUE, then genoud will search for solution among integers when parameters are optimized.
With integer parameters, genoud never uses information about derivatives. It implies that the BFGS optimizer is never used — i.e., the BFGS flag is set in FALSE. This also implies that the P9 operator (local minimum crossover ) is reset, and that checking a gradient (as a criterion of convergence) is disabled. Despite where other options were set, data.type.int has a priority — i.e., if genoud states that the search should be performed by integer area of parameters, information about the gradient is never considered.
There is no option that enables to mix integer parameters with a floating point. If you wish to mix these two types, then an integer parameter can be indicated, and the integer range can be transformed to the range with a floating point in the objective function. For example, you need to obtain the search network from 0.1 to 1.1. You indicate genoud to search from 10 to 110, and then divide this parameter by 100 in the fitness function.
- hessian = FALSE. When this flag is set in TRUE, genoud returns the Hessian matrix in a solution as a part of its return list. A user can use this matrix to calculate standard errors.
- unif.seed = 812821. This sets seed for a generator of a pseudo random figure with a floating point in order to use genoud. Value by default of this seed 81282. genoud uses its personal internal generator of pseudo random figures (Tausworthe-Lewis-Payne generator) to allow recursive and parallel calls to genoud.
- int.seed = 53058. This sets seed for an integer generator that uses genoud. The default value of seed is 53058. genoud uses its personal internal generator of pseudo random figures (Tausworthe-Lewis-Payne generator) to allow recursive and parallel calls to genoud.
- print.level = 2. This variable manages the level of printing what genoud does. There are 4 possible levels: 0 (minimum print), 1 (normal), 2 (detailed) and 3 (debugging). If level 2 is selected, then genoud will print details about population in every generation.
- share.type = 0. If share.type equals 1, then genoud will check at the start if the project file exists (see project.path). If this file exists, it initializes its output population by using it. This option can be used with lexical, but not the transform option.
Operators. Genoud has and uses 9 operators. Weights are integer values that are assigned to each of these operators (P1... P9). Genoud calculates the total s = P1+P2 +... +P9. Weights that equal W_n = s / (P_n) are assigned to each operator. The number of operator calls normally equals c_n = W_n * pop.size.
Р6 operators (Simple crossover) and Р8 (Heuristic crossover) require an even number of species to proceed with operation — in other words they require two parents. Therefore, the pop.size variable and sets of operators must be specific to ensure that these three operators have an even number of species. If it doesn't happen, genoud automatically increases the population, in order to meet this restriction.
Strong checks of uniqueness were built in the operators to guarantee that operators will produce children that are different from their parents, but it doesn't always occur.
Evolutionary algorithm in rgenoud uses nine operators that are mentioned below.
- P1 = 50 – Cloning. Cloning operator simply makes copies of the best test solution in the current generation (independent from this operator, rgenoud always saves one sample of the best test solution).
Universal mutation, boundary mutation and heterogeneous mutation affect the only test solution.
- P2 = 50 – Universal mutation. Universal mutation changes one parameter in the test solution with a random value evenly distributed on a domain defined for the parameter.
- P3 = 50 – Boundary mutation. Boundary mutation changes one parameter with one of the boarders of its domain.
- P4 = 50 – Heterogeneous mutation. Heterogeneous mutation decreases one parameter to one of the boarders with a total of decrease decreasing when the number of generations approaches to indicated maximum number of generations.
- P5 = 50 – Multifaceted crossover. Multifaceted crossover (inspired by simplex search, Gill and other. 1981, p. 94–95), calculates test solution that has a convexity combination of the same number of test solutions as parameters.
- P6 = 50 – Simple crossover. Simple crossover calculates two test solutions from two input test solutions, by changing values of parameters between solutions after randomly dividing solutions in a selected point. This operator can be particularly efficient if arranging parameters in every test solution is sequential.
- P7 = 50 – Integer heterogeneous mutation. Integer heterogeneous mutation makes heterogeneous mutation for all parameters in test solution.
- P8 = 50 – Heuristic crossover. Heuristiccrossover uses two test solutions for a new solution located along the vector that begins in one test solution.
- P9 = 0 — Local minimum crossover: BFGS. Local minimum crossover calculates a solution for a new consideration in two steps. First BFGS performs a preliminary set number of iterations started from the input solution; then, convexity combination of input solutions is calculated, and BFGS is iterated.
Remarks:
The most important options that affect the quality are those that define the size of population (pop.size) and the number of generations performed by the algorithm (max.generations, wait.generations, hard.generation.limit and gradient.check). The search performance, as expected, is improved if the size of population. and the number of generations performed by the program will increase. These and other options should be corrected for various problems manually. Please pay more attention at the search areas (Domains and default.domains).
Linear and non-linear restrictions among parameters can be presented by users in their fitness functions. For example, if the total of 1 and 2 parameters is below 725, then this condition can be embedded into the fitness function, a user will maximize genoud, : if((parm1 + parm2)>= 725) {return (-99999999)}. In this example, a very bad fitness value will be returned to genoud, if a linear restriction is violated. Then genoud will attempt to find values of parameters that will satisfy the restriction.
We will write our fitness function. It should be able to calculate:
MACD
signals
quality rate
# fitness function-------------------------fitness <- function(param, test = FALSE){
require(TTR)
require(magrittr)
# define variables
x <- pr[param[1]]
nFast <- param[2]
nSlow <- param[3]
nSig <- param[4]
macdType <- MaType[param[5]]
sigType <- MaType[param[6]]
percent <- per[param[7]]
len <- param[9]*100
# linear restriction for macd
if (nSlow <= nFast) return(-Inf)
# calculate macd
md <- MACD(x = x, nFast = nFast, nSlow = nSlow,
nSig = nSig, percent = TRUE,
maType = list(list(macdType),
list(macdType),
list(sigType)))
# calculate signals and shift to the right by 1 bar
sig <- signal(md, param[8]) %>% Lag()
#calculate balance on history with len length
bal <- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))
if(test)
{bal <<- cumsum(tail(sig, len) * tail(price[ ,'CO'], len))}
# calculate quality ration (round to integer)
K <- ((tail(bal,1)/length(bal))* 10 ^ Dig) %>% floor()
# return the obtained optimization criterion
return(unname(K))
}
Below is a listing of calculating all variables and functions
require(Hmisc) # Types of the average = 4 ------------------------------------------- MaType <- Cs(SMA, EMA, DEMA, ZLEMA) require(dplyr) # Types of prices = 4 ----------------------------------------------- pr <- transmute(as.data.frame(price), Close = Close, Med = Med, Typ = (High + Low + Close)/3, WClose = (High + Low + 2*Close)/4) # how to calculate? per <- c(TRUE, FALSE) # Types of signals = 3 -------------------------- signal <- function(x, type){ x <- na.omit(x) dx <- diff(x[ ,1]) %>% na.omit() x <- tail(x, length(dx)) switch(type, (x[ ,1] - x[ ,2]) %>% sign(), sign(dx), ifelse(sign(dx) == 1 & sign(x[ ,1]) == 1, 1, ifelse(sign(dx) == -1 & sign(x[ ,1]) == -1,-1, 0)) ) } # initial configuration--------------------------- par <- c(2, 12, 26, 9, 2, 1, 1, 3, 5) # search area-------------------------------------- dom <- matrix(c(1, 4, # for types of prices 8, 21, # for fast МА period 13, 54, # for slow МА period 3, 13, # for signal MA period 1, 4, # МА type for fast and slow 1, 4, # MA type for signal 1, 2, # percent type 1, 3, # signal option 3,10), # history length [300:1000] ncol = 2, byrow = TRUE) # create cluster from available processing cores puskCluster<-function(){ library(doParallel) library(foreach) cores<-detectCores() cl<-makePSOCKcluster(cores) registerDoParallel(cl) #clusterSetRNGStream(cl) return(cl) }
Define quality ration with initial (usually by default) parameters
> K <- fitnes(par, test = TRUE) > K [1] 0 > plot(bal, t="l")
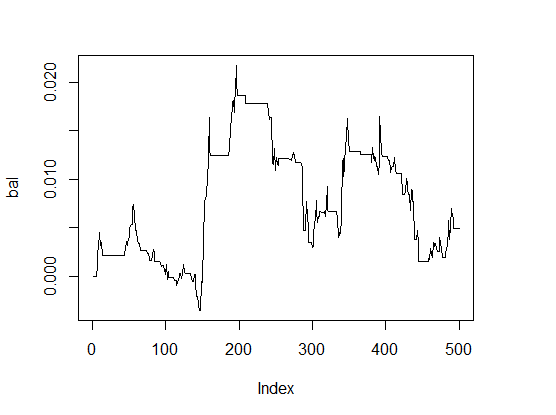
Fig.1 Balance with parameters by default
The results are very bad.
In order to compare calculation speed, we will perform optimization on one core and on the cluster out of two processing cores.
On one core:
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 300, wait.generation = 50, hard.generation.limit = FALSE, starting.values = par, Domains = dom, boundary.enforcement = 1, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No significant improvement in 50 generations. Solution Fitness Value: 1.600000e+01 Parameters at the Solution: X[ 1] : 1.000000e+00 X[ 2] : 1.400000e+01 X[ 3] : 2.600000e+01 X[ 4] : 8.000000e+00 X[ 5] : 4.000000e+00 X[ 6] : 1.000000e+00 X[ 7] : 1.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solution Found Generation 5 Number of Generations Run 56 Thu Mar 24 13:06:29 2016 Total run time : 0 hours 8 minutes and 13 seconds
Optimal parameters (henotype)
> pr.max$par [1] 1 14 26 8 4 1 1 1 4
We decode (phenotype):
- price type pr[ ,1]= Close
- nFast = 14
- nSlow = 26
- nSig = 8
- macdType = ZLEMA
- sigType = SMA
- percent = TRUE
- signal = intersection of macd and signal lines
- history length = 400 bars.
Let's see how the balance line with optimal parameters appears. For this purpose we will perform a fitness function with these parameters and with the test = TRUE option.
> K.opt <- fitnes(pr.max$par, test = TRUE) > K.opt [1] 16 > plot(bal, t="l")
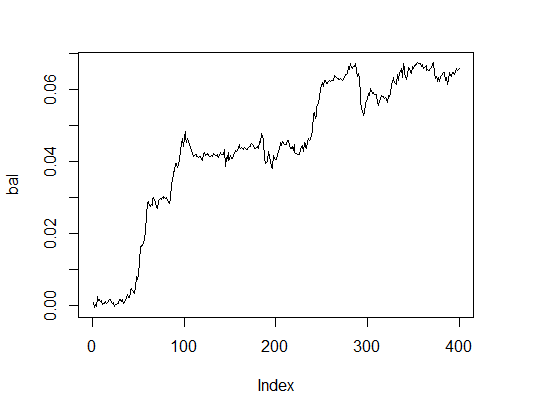
Fig.2. Balance with optimal parameters
This is an acceptable result that an Expert Advisor can operate with.
We will calculate the same on the cluster that contains two cores
# start the cluster
cl <- puskCluster()
# maximize fitness function
# send necessary variables and functions to every core in the cluster
clusterExport(cl, list("price", "pr", "MaType", "par", "dom", "signal",
"fitnes", "Lag", "Dig", "per" ) )
pr.max <- genoud(fitnes, nvars = 9, max = TRUE,
pop.size = 500, max.generation = 300,
wait.generation = 50,
hard.generation.limit = FALSE,
starting.values = par, Domains = dom,
boundary.enforcement = 1,
data.type.int = TRUE,
solution.tolerance = 0.01,
cluster = cl,
print.level = 2) # only for experiments.
# To set in 0 in EA
# stop the cluster
stopCluster(cl)
'wait.generations' limit reached.
No significant improvement in 50 generations.
Solution Fitness Value: 1.300000e+01
Parameters at the Solution:
X[ 1] : 1.000000e+00
X[ 2] : 1.900000e+01
X[ 3] : 2.000000e+01
X[ 4] : 3.000000e+00
X[ 5] : 1.000000e+00
X[ 6] : 2.000000e+00
X[ 7] : 1.000000e+00
X[ 8] : 2.000000e+00
X[ 9] : 4.000000e+00
Solution Found Generation 10
Number of Generations Run 61
Thu Mar 24 13:40:08 2016
Total run time : 0 hours 3 minutes and 34 seconds
The time seems much better, but the quality is slightly lower. In order to solve even such a simple task, it is important to "play around" with parameters.
We will calculate the simplest option
pr.max <- genoud(fitnes, nvars = 9, max = TRUE, pop.size = 500, max.generation = 100, wait.generation = 10, hard.generation.limit = TRUE, starting.values = par, Domains = dom, boundary.enforcement = 0, data.type.int = TRUE, solution.tolerance = 0.01, cluster = FALSE, print.level = 2) 'wait.generations' limit reached. No significant improvement in 10 generations. Solution Fitness Value: 1.500000e+01 Parameters at the Solution: X[ 1] : 3.000000e+00 X[ 2] : 1.100000e+01 X[ 3] : 1.300000e+01 X[ 4] : 3.000000e+00 X[ 5] : 1.000000e+00 X[ 6] : 3.000000e+00 X[ 7] : 2.000000e+00 X[ 8] : 1.000000e+00 X[ 9] : 4.000000e+00 Solution Found Generation 3 Number of Generations Run 14 Thu Mar 24 13:54:06 2016 Total run time : 0 hours 2 minutes and 32 seconds
This shows a good result. And what about balance?
> k [1] 15 > plot(bal, t="l")
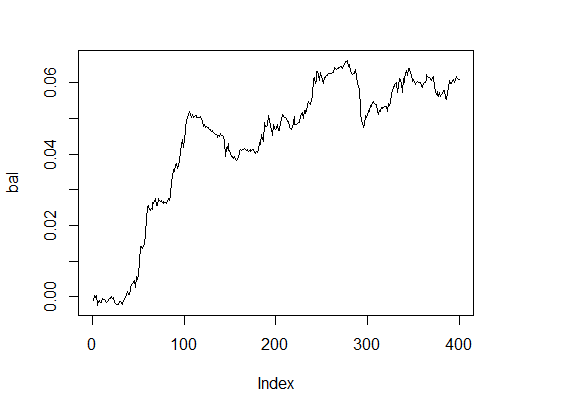
Fig.3. Balance with optimal parameters
Very decent result within reasonable time.
Let's conduct few experiments to compare results of genetic algorithms with evolutionary algorithms. First, we will test SOMA(Self-Organising Migrating Algorithm) implemented in the "soma" package.
Self-organizing general-purpose migrating algorithm of stochastic optimization — approach similar to genetic algorithm, although it is based on the concept of "migration" series with a fixed set of species, instead of development of further generations. It is resistant to local minimums and can be applied to any task of minimizing expenses with limited area of parameters. The main function:
soma(costFunction, bounds, options = list(), strategy = "all2one", …) Arguments
Details
There are multiple options for setting optimization and criteria of its completion. Default values used here are recommended by the author Zelinka (2004).
- pathLength: Distance until the leader that species can migrate to. Value 1 corresponds to leader position, and value above 1 (recommended) considers certain re-regulation. 3 is indicated by default.
- stepLength: Minimal step used to evaluate possible steps. It is recommended that the path length wasn't an integer multiple of this value. Default value is 0.11.
- perturbationChance: Probability that selected parameters will change on any given stage. Default value 0.1.
- minAbsoluteSep: The least absolute difference between maximum and minimum values of the price function. If the difference falls below this minimum, then the algorithm is ended. Default value is 0. It means that this termination criterion will never be satisfied.
- MinRelativeSep: The least relative difference between maximum and minim values of the price function. If the difference falls below this minimum, then the algorithm is ended. Default value is 0,001.
- nMigrations: Maximum number of migrations for termination. Default value is 20.
- populationSize: Number of species in population. It is recommended that this value is slightly higher than the number of optimized parameters, and it shouldn't be below 2. Default value equals 10.
Since the algorithm performs minimization only, we will review our fitness function so it would provide value with an opposite sign and start optimization.
require(soma) x <- soma(fitnes, bounds = list(min=c(1,8,13,3,1,1,1,1,3), max = c(4,21,54,13,4,4,2,3,10)), options = list(minAbsoluteSep = 3, minRelativeSep = -1, nMigrations = 20, populationSize = 20), opp = TRUE) Output level is not set; defaulting to "Info" * INFO: Starting SOMA optimisation * INFO: Relative cost separation (-2.14) is below threshold (-1) - stopping * INFO: Leader is #7, with cost -11
Best parameters:
> x$population[ ,7] [1] 1.532332 15.391757 37.348099 9.860676 1.918848 [6] 2.222211 1.002087 1.182209 3.288627 Round to > x$population[ ,7]%>% floor [1] 1 15 37 9 1 2 1 1 3
Best value in the fitness function = 11. This is acceptable for practical application, but there is space for improvement.
The algorithm is fast, but unstable in results and requires fine tuning.
Generalized Simulated Annealing Function
This algorithm is implemented in the «GenSA” package. This function can perform the search for a global minimum with a complex non-linear target function with a large number of optimums.
GenSA(par, fn, lower, upper, control=list(), …)
Arguments:
- par — Initial values for components that must be optimized. NULL is by default, and in this case, default values will be automatically generated.
- fn — function that will be minimized. Few vector parameters are set for minimizing the function . It should return a scalar result.
- lower – vector with length(par) length. Lower boarder of components.
- upper — vector with length(par) length. Upper boarder of components.
- … allows user to send additional arguments of the fn function.
- control — control argument. This is a list that can be used to manage the algorithm behavior.
- maxit – Integer. Maximum number of algorithm iteration.
- threshold.stop — Numerical. The program will terminate upon the expected value of the threshold.stop target function. Default value — NULL.
- nb.stop.improvement — Integer. The program will be terminated if there are no improvements throughout nb.stop.improvement steps.
- smooth — logical. TRUE, when target function is smooth or differentiated in the area of parameters almost everywhere; otherwise FALSE. Default value — TRUE
- temperature — Numerical. Initial value of temperature.
- simple.function — Logical. TRUE means that the target function has only few local minimums. FALSE is set by default, which means that the target function is complicated with many local minimums.
- trace.mat — Logical. TRUE by default. This means that tracing matrix will be available in the returned value of GenSA call.
Values of control components are set by default for a complex optimization task. For a regular optimization task with average complexity GenSA can find a reasonable solution quickly, therefore it is advisable for a user to let GenSA terminate earlier:
by setting threshold.stop, if threshold.stop is an expected value of the function;
or by terminating max.time, if a user simply wants to run GenSA for max.time seconds;
or by setting max.call, if a user simply wants to run GenSA within max.call calls of functions.
For very complex optimization tasks, a user should increase maxit and temperature.
Let's run optimization by limiting the maximum time of performance by 60 seconds.
require(GenSA) pr.max <- GenSA(par, fitnes, lower = c(1,8,13,3,1,1,1,1,3), upper = c(4,21,54,13,4,4,2,3,10), control = list(verbose = TRUE, simple.function = TRUE, max.time = 60), opp = TRUE)
Value of fitness function and value of optimal parameters:
> pr.max$value * (-1) [1] 16 > par1 <- pr.max$par > par1 [1] 1.789901 14.992866 43.854988 5.714345 1.843307 [6] 1.979723 1.324855 2.639683 3.166084
Round off:
> par1 <- pr.max$par %>% floor [1] 1 14 43 5 1 1 1 2 3
Calculate value of the fitness function with these parameters and see the balance line:
> f1 <- fitnes(par1, test = TRUE) > plot(-1 * bal, t="l")
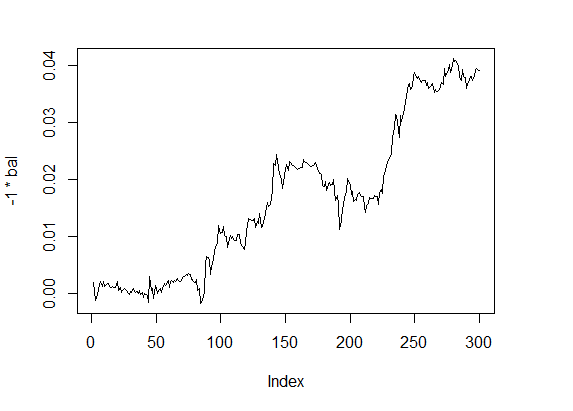
Fig.4 Balance 4
Quality indicators — on a good level, and calculations are surprisingly fast.
These and many similar algorithms (packages dfoptim, nlopt,CEoptim, DEoptim,RcppDE etc.) optimize the function by one criterion. For multiple criteria optimization, the mco package is intended.
7. Ways and methods of improving qualitative characteristics
The experiments we conducted showed the efficiency of genetic algorithms. For a further improvement of qualitative indicators it is recommended to perform additional researches with application of:
- multicriterial optimization. For example, to perform optimization of the quality ration and its maximum drawdown. The "mco" package implements such opportunity.
- try to implement a dynamic self-organization of GA parameters. The package for possible implementation — "GA". It provides a wide range of operators for selection, crossover and mutation.
- to test for a possibility of applying a genetic programming in the trading system.
Conclusion
We have considered the basic principles set in evolutionary algorithms, their different types and features. Using a simple MACDSample Expert Advisor we have used the experiments to show that applying the optimization of parameters even for such elementary TC has a considerable positive effect.
Time of performing optimization and the simplicity in programing allow to perform it during operation of EA without market entry. And the lack of strict restrictions on the type of optimization parameters allow to implement the most diverse type of optimization on various stages of EA operation.
The most important part of work is to write the fitness function correctly.
I hope this article will help you understand that it is not difficult, so you can attempt to implement optimization of your Expert Advisors yourself.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/2225
 Graphical Interfaces VI: the Slider and the Dual Slider Controls (Chapter 2)
Graphical Interfaces VI: the Slider and the Dual Slider Controls (Chapter 2)
 Graphical Interfaces VI: the Checkbox Control, the Edit Control and their Mixed Types (Chapter 1)
Graphical Interfaces VI: the Checkbox Control, the Edit Control and their Mixed Types (Chapter 1)
 Universal Expert Advisor: A Custom Trailing Stop (Part 6)
Universal Expert Advisor: A Custom Trailing Stop (Part 6)
 Universal Expert Advisor: Pending Orders and Hedging Support (Part 5)
Universal Expert Advisor: Pending Orders and Hedging Support (Part 5)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use