sDotToLineDist - MetaTrader 5脚本

函数参数:

• double LX1 - 该线的第一个点的 X 坐标;
• double LY1 - 该线的第一个点的 Y 坐标;
• double LX2 - 该线的第二个点的 X 坐标;
• double LY2 - 该线的第二个点的 Y 坐标;
• double DX - 点的 X 坐标;
• double DY - 点的 Y 坐标.

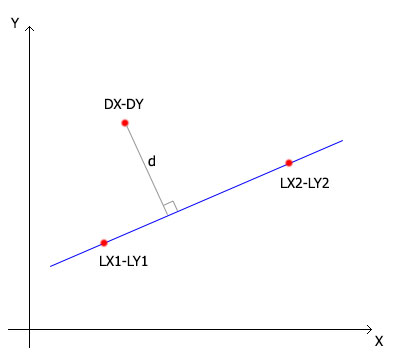
计算原理

根据线上两点的坐标，我们得到线公式: y=a+k*x。 k 系数确定线的斜率，即 x 坐标中每个变化单位导致的 y 坐标的变化。 k 系数计算如下:

double K=(LY2-LY1)/(LX2-LX1);

a 常数确定线的值，如果 x=0，即对应于线与 y 轴交叉的等级。 知道线上其中一个点的斜率系数和 X 坐标，我们计算 a:

double LA=LY1-K*LX1;

从点到线的距离根据线绘制的垂线确定。 如果逆时针旋转图纸 90 度，则 d 线将具有与主线相同的斜率，但符号相反。 知道一个点的斜率和坐标，我们可以得到线的方程，但在这种情况下，可以采用 x=a-ky的形式。 所以, a 常量:

double DA=DX+K*DY;

有两条线的公式，我们找到它们的交点。 为此目的，我们将第一行公式所表示的 y 替换为第二行的公式，进行一些变换并获得交点的 x 坐标:

double CX=(DA-K*LA)/(1.0+K*K);

然后将公式中的结果 x 代入第一行，并获得交点的 y 坐标:

double CY=LA+K*CX;

知道了两点的坐标，我们可以计算它们沿 x 轴和 y 轴 (轴上的投影) 之间的距离。 进而，使用毕达哥拉斯定理，计算距离:

MathSqrt(MathPow(DX-CX,2)+MathPow(DY-CY,2))

俄语讨论内容在 https://www.mql5.com/ru/forum/237198。 您也可以在此评论中讨论想法。