Bu temelde yanlıştır.
İlk olarak, Rusça konuşalım ve "basıklık" ve "adalılığı" kabul edilen terimle - basıklık katsayısı veya sadece basıklık olarak adlandıralım.
İkinci olarak, "adalılık" ve "şişman kuyruklar" genel durumda hiçbir şekilde ilişkili değildir. İşte bir karşı örnek - Laplace dağılımı (iki taraflı üstel), ki finansal zaman serilerinin büyük çoğunluğunun grafiklerinin buna uyduğu söylenmelidir. Fazlası 3'e eşittir (yani tepesi normal dağılımdan daha keskindir), ancak kuyrukları kalındır - exp(-x) yasasına göre azalırlar, yani Gauss exp(-x^2) yasasından daha yavaştırlar.
Bu temelde yanlıştır.
İlk olarak, Rusça konuşalım ve "basıklık" ve "adalılığı" kabul edilen terimle - basıklık katsayısı veya sadece basıklık olarak adlandıralım.
İkinci olarak, "adalılık" ve "şişman kuyruklar" genel durumda hiçbir şekilde ilişkili değildir. İşte bir karşı örnek - Laplace dağılımı (iki taraflı üstel), ki finansal zaman serilerinin büyük çoğunluğunun grafiklerinin buna uyduğu söylenmelidir. Fazlası 3'e eşittir (yani tepesi normal dağılımdan daha keskindir), ancak kuyrukları sadece kalındır - exp(-x) yasasına göre azalırlar, yani Gaussian exp(-x^2)'den daha yavaştır.
Dahası, kendi başına bir "Aşırılık" kavramı yoktur, başka bir kavram olan "Dağılımın Aşırılığı" için bir ölçü olan "Aşırılık Oranı" kavramı vardır ve bu kavram yalnızca tek modlu dağılımlar için tanımlanmıştır. Dolayısıyla, bu katsayıyı doğru bir şekilde kullanabilmek için, öncelikle ampirik dağılım fonksiyonunu belirlemek gerekir ki bu matematik açısından önemsiz bir görev değildir ve ikinci olarak, bazı olasılık kriterleri çerçevesinde, dağılımın tek bir moda sahip olduğu hipotezini kontrol etmek ve kabul etmek gerekir ki bu finansal seriler için her zaman yerine getirilmez ve aynı zamanda önemsiz bir görevdir. Bu adımlar olmaksızın, "Aşırı katsayı" gerektiriyorsa, daha fazla hesaplama yapmak imkansızdır.
P.S..
Test, serinin varsayılan model için geçerli olmadığını söylerse ne yapılacağı hakkında hiçbir şey yazılmamıştır.
Neden ve neye dayanarak başka bir serinin değil de "getiri" olarak adlandırılan bir serinin kullanıldığı hakkında hiçbir şey söylenmemektedir.
Uygulamada, varlık getirileriyle çalışmanın doğrudan varlık fiyatlarıyla çalışmaya tercih edilmesinin ana nedeni, getirilerin daha cazip istatistiksel özelliklere sahip olmasıdır.
alsu:
...Rusça konuşalım ve "basıklık" ve "adalılığı" kabul edilen terimle adlandıralım - aşırılık katsayısı veya sadece aşırılık....
Özellikle alsu 'nun "katsayı" ve "fazlalık" kelimelerini Rusça olarak görmesi hoşuma gitti...
alsu:
İkinci olarak, "adalılık" ve "kalın kuyruklar" genellikle birbiriyle ilişkili değildir. İşte bir karşı örnek - Laplace dağılımı (iki taraflı üstel), belirtmek gerekir ki, finansal zaman serilerinin büyük çoğunluğunun grafikleri buna uymaktadır. Fazlası 3'e eşittir (yani tepesi normal dağılımdan daha keskindir), ancak kuyrukları sadece kalındır - exp(-x) yasasına göre azalırlar, yani Gaussian exp(-x^2)'den daha yavaştır.
Genel olarak ilişkili olduğuna inandığım şey tam olarak budur.
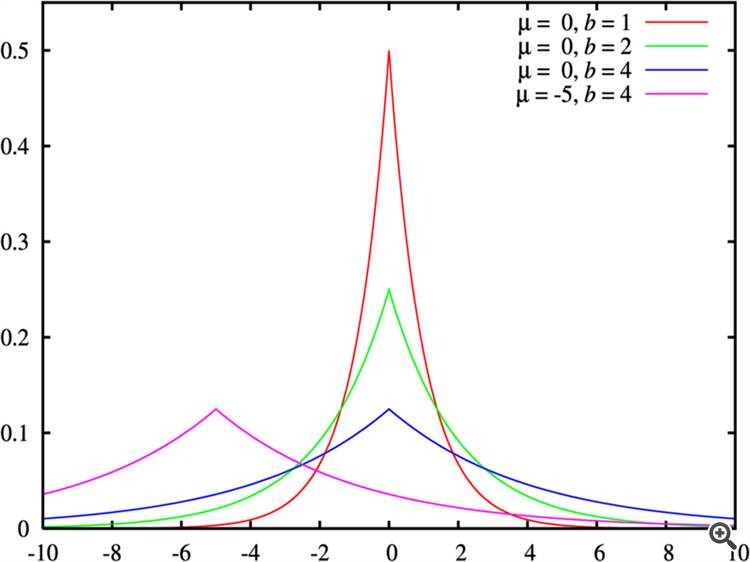
"Daha az basıklık-daha kalın kuyruklar "ın bir örneği Şekil "Farklı parametreli Laplace dağılımları "nda gösterilmiştir .
Yazıma sadece şu cümleyi eklemek isterim: "Bir dizi getirinin dağılımı, normal dağılıma göre daha sık olarak şişman kuyruk davranışı sergiler." "Şişman kuyruklar" olgusu İngilizce literatürde aşırı basıklık olarak adlandırılır. Dağılımları bu tür kuyruklara sahip olan seriler leptokurtic olarak adlandırılır ve pozitif basıklığa sahiptir (normal dağılımın basıklığını aşar).
O zaman basıklık katsayısı hakkında:
Normal dağılım sıfır basıklığa sahiptir, γ2 = 0.
Eğer dağılımın kuyrukları "daha hafif" ve tepe noktası normal dağılımdan daha keskin ise, o zaman γ2 > 0 olur.
Eğer dağılımın kuyrukları "daha ağır" ve tepe noktası normal dağılıma göre daha "basık" ise, o zaman γ2 < 0 olur.
Böyle bir öneriyi sadece makaleme eklerdim:
Yazıma sadece şu cümleyi eklemek isterim: "Bir dizi getirinin dağılımı, normal dağılıma göre daha sık olarak şişman kuyruk davranışı sergiler." "Şişman kuyruklar" olgusu İngilizce literatürde aşırı basıklık olarak adlandırılır. Dağılımları bu tür kuyruklara sahip olan seriler leptokurtic olarak adlandırılır ve pozitif basıklığa sahiptir (normal dağılımın basıklığını aşar).
Sonra basıklık katsayısı hakkında:
Normal dağılım sıfır basıklığa sahiptir, γ2 = 0.
Eğer dağılımın kuyrukları "daha hafif" ve tepe noktası normal dağılımdan daha keskin ise, o zaman γ2 > 0 olur.
Eğer dağılımın kuyrukları "daha ağır" ve tepe noktası normal dağılıma göre daha "basık" ise, o zaman γ2 < 0'dır.
Siz terimler hakkında tartışırken, ben bu makaledeki fikirleri kullanarak bir gecede zaten bazı karlı EA'lar oluşturdum. :-)
Ancak, oldukça istikrarlı olmalarına rağmen kârları çok düşük (12 yıllık geçmişe bakıldığında grafikler güzel bir şekilde büyüyor). Makalede açıklanan yöntemlerle tespit edilen korelasyonlar oldukça zayıftır ( serilerin otokorelasyon katsayıları yaklaşık 0,01'dir, istisnai durumlarda hangi fiyat türevlerinin ilişkili olduğuna bağlı olarak 0,1'e yaklaşır) ve ticaret yaparken bunlardan elde edilen kar, spread tarafından güçlü bir şekilde yenilir. Yalnızca güçlü sinyaller geldiğinde alım satım yapmak için bir filtre eklemek zorunda kaldım, aksi takdirde karlılık eğrisi yarı düz bir şekilde düşecekti.
Her durumda yazara teşekkürler. Fikirler çok değerli. Eleştirmenlerin yazarın burnunu matematik teorisinin uçurumlarına sokmaması gerektiğini düşünüyorum, ancak makaleyi pratik deneyler için geniş bir alanın göstergesi olarak düşünün.
Siz terimler hakkında tartışırken, ben bu makaledeki fikirleri kullanarak bir gecede zaten bazı karlı EA'lar oluşturdum. :-)
Ancak, oldukça istikrarlı olmalarına rağmen kârları çok düşük (12 yıllık geçmişe bakıldığında grafikler güzel bir şekilde büyüyor). Makalede açıklanan yöntemlerle tespit edilen korelasyonlar oldukça zayıftır (serilerin otokorelasyon katsayıları yaklaşık 0,01'dir, istisnai durumlarda hangi fiyat türevlerinin ilişkili olduğuna bağlı olarak 0,1'e yaklaşır) ve ticaret yaparken bunlardan elde edilen kar, spread tarafından güçlü bir şekilde yenilir. Yalnızca güçlü sinyaller geldiğinde alım satım yapmak için bir filtre eklemek zorunda kaldım, aksi takdirde karlılık eğrisi yarı düz bir şekilde düşecekti.
Her durumda yazara teşekkürler. Fikirler çok değerli. Bence eleştirmenler yazarın burnunu matematik teorisinin uçurumlarına sokmamalı, makaleyi pratik deneyler için geniş bir alanın göstergesi olarak görmeli.
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Yeni makale Grafiklerin Analizine Ekonometrik Yaklaşım yayınlandı:
Bu makale ekonometrik analiz yöntemlerini, otokorelasyon analizini ve özellikle koşullu varyans analizini açıklamaktadır. Burada açıklanan yaklaşımın faydası nedir? Doğrusal olmayan GARCH modellerinin kullanımı, analiz edilen serilerin matematiksel açıdan resmi olarak temsil edilmesine ve belirli sayıda adım için bir tahmin oluşturulmasına olanak tanır.
Analizin amacının zamanserisi olan bir fiyat serisi olduğu açıktır.
Ekonometristler zaman serilerini frekans yöntemleri (spektrum analizi, dalgacık analizi) ve zaman alanı yöntemleri (çapraz korelasyon analizi, otokorelasyon analizi) açısından inceler. Okuyucuya frekans yöntemlerini açıklayan “Spektrumu Analizini Oluşturma” makalesi zaten sunulmuştur. Şimdi zaman alanı yöntemlerine, otokorelasyon analizine ve özellikle koşullu varyans analizine bir göz atmanızı öneriyorum.
Doğrusal olmayan modeller fiyat zaman serilerinin davranışını doğrusal olanlardan daha iyi tanımlar. Bu nedenle, bu makalede doğrusal olmayan modelleri incelemeye odaklanacağız.
Fiyat zaman serileri yalnızca belirli ekonometrik modeller tarafından dikkate alınabilecek özel niteliklere sahiptir. İlk olarak bu tür nitelikler şunlardır: “ağır kuyruklu” dağılım, volatilite kümelenmesi ve kaldıraç etkisi.
Yazar: Denis Kirichenko