Ранее я уже немного рассуждал о переходе от модели с игровой неопределённостью к модели с вероятностной неопределённостью (раз, два, три). Решил, что стоит добавить простенький пример подобного перехода.
Исходить буду из той же игры меньшинства. Цена - целое число x=x(n), время n - целое неотрицательное. В каждый момент времени какая-то доля игроков u, 0<=u<= 1 ставит на движение цены на единичку вверх, а остальные 1-u - на движение вниз.
Стоит оговориться, что для честного биржевого рынка всегда u=1-u -> u=0.5. Таким образом, здесь нами моделируется некий внебиржевой рынок (или нечестный биржевой). Соотношение u и 1-u обычно называется сентиментом рынка.
Далее, несколько изменю правило игры меньшинства (в сравнении с предыдущими записями) для определения направления изменения цены и того, кто из игроков выигрывает. Теперь решение будет приниматься не детерминировано (против большинства), а с некоторой вероятностью, зависящей от u: p=P(u), где p означает вероятность цены сдвинуться вверх. Будем считать это изменение правил попыткой учесть неопределённость нашего знания о рынке.
Помимо этого, после того как цена меняется, происходит изменение величины u: u(n)=U(u(n-1), d(n)), где n - момент времени, d(n)=x(n)-x(n-1) - прирост цены к этому моменту, U() - некоторая функция двух аргументов.
Попробуем подобрать какие-нибудь функции P() и U() и смоделировать «цену». Общие свойства этих функций: P() - не возрастающая функция на отрезке [0; 1], а значения функции U() всегда принадлежат отрезку [0; 1], а также U(u, 1)>u и U(u, -1)<u. То есть, при увеличении доли игроков ставящих на рост цены, вероятность этого самого роста цены либо падает, либо не меняется (верно и наоборот). После роста цены доля игроков ставящих на рост цены на следующем шаге растёт (и наоборот).
Возьмём P(u)=1-u, U(u, -1)=u-e*u, U(u, 1)=u+e*(1-u). Функция U() устроена здесь так, что фиксированная доля e, 0<e<1, игроков не угадавших направление движения, меняет своё мнение на противоположное. Проведём моделирование посредством языка R. В начальный момент времени n=0, x(0)=0, u(0)=p(0)=0.5. Максимальное время n=N. Код на R:
e <- 0.2; N <- 200 P <- function(u) 1-u U <- function(u, d){if(d<0) u <- u*(1-e) else u <- u+e*(1-u); u} u <- 0.5; x <- rep(0,N+1) for (n in 1:N) { p <- P(u) d <- sample(c(1,-1),1,prob = c(p,1-p)) x[n+1] <- x[n] + d u <- U(u,d) } rw <- cumsum(sample(c(1,-1),N+1, replace = TRUE)) # random walk yx <- max(x,rw); yn <- min(x,rw) plot(rw, type = "l",col = "blue", ylim = c(yn,yx)) lines(x, type = "l", col="green")
Рисунок ниже - результат одного запуска моделирования. Наш ряд изображён зелёной линией, а синей - случайное блуждание для сравнения. Заметно достаточно флэтовое поведение нашего ряда в сравнении с СБ.
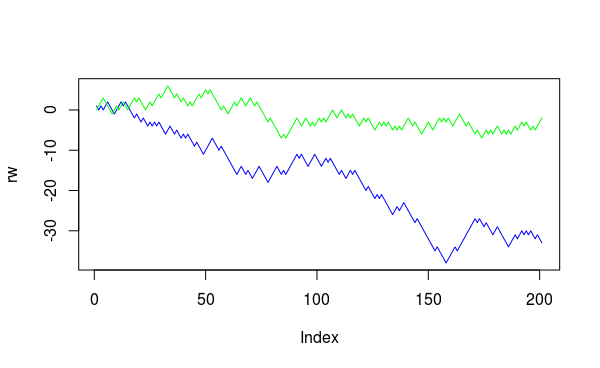
Не то чтобы этот пример имеет практическую ценность, но некоторую пищу для размышлений всё же предоставляет.
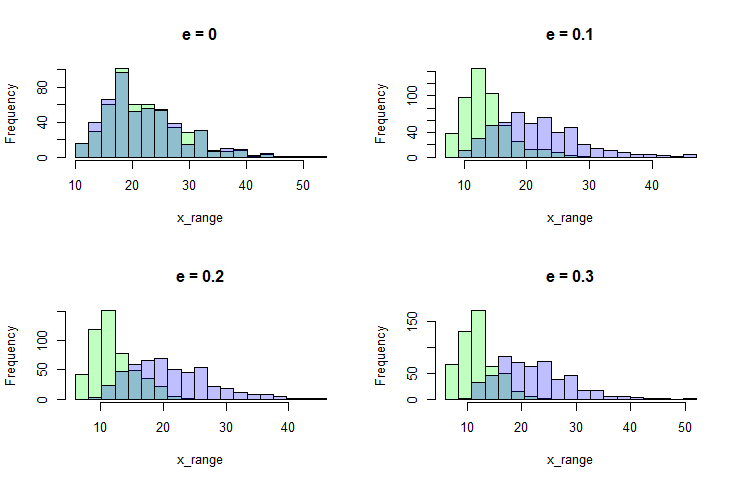
Отличие размаха смоделированного процесса x[n] от размаха СБ при разных значениях e вполне очевидно уже по гистограмам, начиная с e=0.1. Можно ещё каким-нибудь способом посмотреть разницу между ними, но смысла пока не вижу.
Гистограммы (x[n] - зеленоватый, СБ - светло-синий, а там где они пересекаются - тёмно-синий):
Код на R для построения гистограмм:
P <- function(u) 1 - u U <- function(u, d, e) { if (d < 0) u <- u * (1 - e) else u <- u + e * (1 - u) u } N <- 200 NR <- 500 par(mfrow = c(2, 2)) for (e in seq(0, 0.3, by = 0.1)) { x_range <- rep(0, NR) rw_range <- rep(0, NR) for (i in 1:NR) { u <- 0.5 x <- rep(0, N + 1) for (n in 1:N) { p <- P(u) d <- sample(c(1,-1), 1, prob = c(p, 1 - p)) x[n + 1] <- x[n] + d u <- U(u, d, e) } rw <- cumsum(sample(c(1,-1), N + 1, replace = TRUE)) # random walk x_range[i] <- max(x) - min(x) rw_range[i] <- max(rw) - min(rw) } x0 <- min(x_range, rw_range) x1 <- max(x_range, rw_range) bs <- seq(x0, x1, length.out = 20) hx <- hist(x_range, breaks = bs, plot = FALSE) hrw <- hist(rw_range, breaks = bs, plot = FALSE) plot(hx, col = rgb(0, 1, 0, 1 / 4), xlim = c(x0, x1), main = paste("e =", e)) plot(hrw, col = rgb(0, 0, 1, 1 / 4), xlim = c(x0, x1), add = T) }
Посмотрел - будет ли разница, если u - доля тех, кто ждёт продолжения движения, а 1-u - доля тех, кто ждёт смены направления движения (персистенцы и антиперсистенцы). Принципиальной разницы не заметил - та же флетовость, растущая с ростом параметра e.


