리퀴드 차트

MetaTrader 5 — 트레이딩 | 12 10월 2021, 16:21

173

개요

H4 타임프레임 또는 그 상위 타임프레임을 갖는 차트가 브로커마다 다르게 나타나더군요. 각 브로커가 위치한 시간대가 다르기 때문이었습니다. 시간대의 차이가 얼마 나지 않아도 동일한 차트 내 일부가 아주 다르게 나타나는 경우도 있었습니다. 한 차트에서는 뚜렷한 반전 패턴이 보였던 반면 다른 차트의 동일한 부분에서는 어떤 뚜렷한 패턴도 나타나지 않았죠.

그걸 보니 우측에 항상 완성된 바가 나타나도록 H1 차트를 다시 그리는 인디케이터를 작성해 보고 싶더라고요. M1을 기준 가격으로 삼았습니다. 1분마다 시간차트가 다시 그려져 한 시간 후에는 동일한 시간에 대한 차트가 60가지로 나타나더라고요. 점점 그 형태가 부드러워지면서 처음에는 전혀 예측할 수 없었던 패턴이 나타났습니다.

그래서 '리퀴드 차트'라고 부르기로 했죠. 플로팅 모드에 따라 기본 시간대에 새로운 바가 생성되거나 정적 시프트 값이 변하는 경우 차트가 '흐릅니다'(다시 그려집니다). '리퀴드 차트' 플로팅 원칙을 알아보고 인디케이터를 작성할 겁니다. 그리고 나서 인디케이터를 이용하는 EA와 패턴을 이용하는 EA에서 효율성이 어떻게 다르게 나타나는지 알아보죠.

1. 플로팅 원칙

시작에 앞서 몇 가지 용어를 설명하겠습니다.

시프트 는 결과 차트 바의 개장가와 소스 차트 바 개장가 사이의 차이입니다.

현재 타임프레임은 소스 차트의 타임프레임입니다.

기본 타임프레임은 결과 차트 내 바 생성을 위해 사용할 가격이 포함된 타임프레임입니다.

기본 피리어드는 현재 피리어드보다 클 수 없습니다. 현재 피리어드는 나머지 없이 기본 피리어드로 나뉘어야 합니다. 현재 피리어드를 기본 피리어드로 나눈 값이 클수록 결과 차트가 여러 버전으로 나타납니다. 하지만 해당 값이 너무 큰 경우 기본 타임프레임의 과거 기록이 필요한 결과 차트 바를 생성하는 데에 충분하지 않을 수 있습니다.

다음의 세 가지 방법으로 차트를 그릴 수 있습니다.

정적 시프트 차트(Static Shift 또는 SS)
개장 모드 동적 시프트 차트(Dynamic Shift, just Open 또는 DSO)
폐장 모드 동적 시프트 차트(Dynamic Shift, expected Close 또는 DSC)

정적 시프트 모드의 경우 바의 오픈 시간은 설정된 시간에 의해 시프트됩니다. 개장 모드 동적 시프트에서는 바가 방금 열린 것처럼 보이며 폐장 모드 동적 시프트에서는 바가 곧 닫힐 것처럼 보입니다.

좀 더 자세히 살펴보죠.

1.1. 정적 시프트 차트

각각의 바의 오픈 시간은 기본 타임프레임에서 설정된 수에 해당하는 분만큼 시프트됩니다. 이것을 시프트라고 합니다. 설정된 시프트가 0인 경우 차트는 소스 차트와 완전히 동일하게 나타나죠. 기본 타임프레임이 15분인 경우 시프트 1은 15분에 해당합니다. 시프트 2는 30분이 되죠.

시프트는 (k-1)보다 클 수 없습니다. 이때 k는 현재 타임프레임을 기본 타임프레임으로 나눈 값입니다. 예를 들어 현재 타임프레임이 H1이고 기본 타임프레임이 M1인 경우 허용 가능한 최대 시프트는 60/1-1=59, 즉 59분이 됩니다. 기본 타임프레임이 M5인 경우 허용 가능한 최대 시프트는 60/5-1=11, 즉 55분이 되죠.

현재 타임프레임이 H1이고 15분의 시프트가 발생하는 경우, 바 오프닝 타임은 00:15, 01:15, 02:15...로 계속됩니다. 현재 타임 프레임이 M15이고 1분의 시프트가 있는 경우에는 바 오프닝 타임은 00:16, 00:31, 00:46, 01:01...이 되죠.

시프트가 임계값에 가까워지면 차트가 소스 차트와 거의 동일하게 나타납니다. 시프트 값이 허용 범위의 중간값에 가까울수록 큰 차이를 보이죠.

정적 시프트 차트

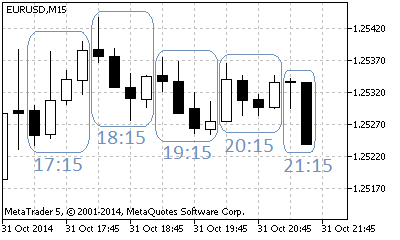
그림 1. 시프트 값이 1인 기본 타임프레임 M15의 시간당 바 형성 예시

1.2. 개장 모드 동적 시프트 차트

기본 타임프레임에서 새로운 바가 나타날 때마다 시프트가 계산됩니다. 차트 가장 끝에서 나타나는 바의 시간이 기본 타임프레임 값을 초과하지 않도록 시프트가 계산됩니다. 현재 타임프레임이 H1이고 기본 타임프레임이 M5인 경우 가장 우측에 위치한 바가 5분 전에 오픈된 것처럼 보일 겁니다.

동적 시프트 차트 바 시작 부분

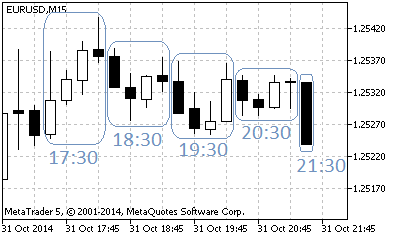
그림 2. 기본 타임프레임 M15를 갖는 개장 모드 동적 시프트 차트의 시간당 바 형성 예시

1.3. 폐장 모드 동적 시프트 차트

개장 모드에서와 마찬가지로 기본 타임 프레임에서 새로운 바가 나타날 때마다 시프트가 다시 계산됩니다. 유일한 차이점은 차트 끝에서 나타나는 바의 시간이 기본 타임프레임과 현재 타임프레임 간의 차이보다 크거나 동일하다는 것이죠. 현재 타임프레임이 H1이고 기본 타임프레임이 M5일 때 가장 우측에 위치한 바는 최대 5분 이내에 닫힐 것처럼 보일 겁니다.

동적 시프트 차트 바 완성 부분

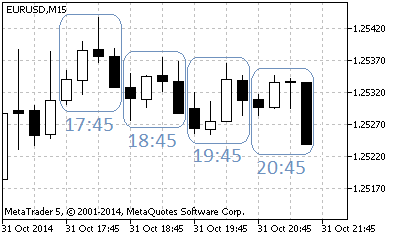
그림 3. 기본 타임프레임 M15를 갖는 폐장 모드 동적 시프트 차트의 시간당 바 형성 예시

2. 데이터 변형

GetRatesLC() 함수는 설정된 시프트를 고려해 과거 기록을 변환하도록 작성되었습니다. 변환된 기록을 MqlRates 유형 구조 배열에 기록하는데요. CopyRates() 함수와 비슷한 셈이죠.

int GetRatesLC(
   int             start_pos    // source for copying
   int             len,         // amount to copy
   MqlRates&       rates[],     // target array
   ENUM_TIMEFRAMES base_period, // basic timeframe
   int&            shift        // shift
   );

-->

매개 변수

start_pos

[in] 현재 타임프레임 첫 엘리먼트 인덱스 데이터 변환 및 버퍼 복사 시작점

len

[in] 복사된 엘리먼트 수

rates[]

[out] MqlRates 유형 배열

base_period

[in] 기본 타임프레임

shift

[in] [out] 시프트 다음의 값을 허용합니다.

값	설명
-2	개장 모드에서 시프트 계산(바 형성 시작)
-1	폐장 모드에서 시프트 계산(바 형성 끝)
0 ... N	설정된 시프트 적용 0에서 N 사이의 값 N=Tcur/Tbase-1 Tcur: 현재 타임프레임, Tbase: 기본 타임프레임

표 1. 허용 가능한 shift 변수

해당 함수가 성공적으로 구현되면 shift는 -2 또는 -1이 전달된 경우 계산된 시프트 값을 수신합니다.

반환값

복사된 엘리먼트 개수 또는 오류 코드

코드	설명
-1	기본 타임프레임 특정 오류
-2	시프트 특정 오류

표 2. 반환된 에러 코드

다음은 liquidchart.mqh 파일의 GetRatesLC() 함수 코드입니다.

int GetRatesLC(int start_pos,int len,MqlRates &rates[],ENUM_TIMEFRAMES base_period,int& shift)
  {
   //--- number of basic timeframes contained in the current one  
   int k=PeriodSeconds()/PeriodSeconds(base_period);
   if(k==0)
      return(-1);//basic timeframe specified incorrectly
   //---
   MqlRates r0[];
   ArrayResize(rates,len);
   if(CopyRates(_Symbol,_Period,start_pos,1,r0)<1)
      return(0);// no data
   //---
   int sh;
   if(shift>=0)
     {
      //--- fixed shift
      if(shift<k)
         sh=shift;
      else
         return(-2);//--- shift specified incorrectly   
     }
   else if(shift==-1)
     {
      //--- shift to be calculated (dynamic, beginning of the bar formation)
      sh=int((TimeCurrent()-r0[0].time)/PeriodSeconds(base_period));
     }
   else if(shift==-2)
     {
      //--- shift to be calculated (dynamic, end of the bar formation)
      sh=1+int((TimeCurrent()-r0[0].time)/PeriodSeconds(base_period));
      if(sh>=k)
         sh = 0;
     }
   else
      return(-2);//shift specified incorrectly       
   //--- opening time of the basic period bar, which is the beginning of the current period bar formation
   //--- synchronization of the time of opening bars takes place relative to the tO time
   datetime tO;
   //--- closing time of the bar under formation, i.e. opening time of the last bar of basic timeframe in the series
   datetime tC;
   tO=r0[0].time+sh*PeriodSeconds(base_period);
   if(tO>TimeCurrent())
      tO-=PeriodSeconds();
   tC=tO+PeriodSeconds()-PeriodSeconds(base_period);
   if(tC>TimeCurrent())
      tC=TimeCurrent();
   int cnt=0;
   while(cnt<len)
     {
      ArrayFree(r0);
      int l=CopyRates(_Symbol,base_period,tC,k,r0);
      if(l<1)
         break;
      //--- time of the bar with the (l-1) index does not have to be equal to tC
      //--- if there is no bar with the tC time, it can be the nearest bar
      //--- in any case its time is assigned to the tC time
      tC=r0[l-1].time;
      //--- check if tO has the correct value and modify if needed.
      while(tO>tC)
         tO-=PeriodSeconds();
      //--- the time values of tO and tC have actual meaning for the bar under formation  
      int index=len-1-cnt;
      rates[index].close=0;
      rates[index].open=0;
      rates[index].high=0;
      rates[index].low=0;
      rates[index].time=tO;
      for(int i=0; i<l; i++)
         if(r0[i].time>=tO && r0[i].time<=tC)
           {
            if(rates[index].open==0)
              {
               rates[index].open= r0[i].open;
               rates[index].low = r0[i].low;
               rates[index].high= r0[i].high;
                 }else{
               if(rates[index].low > r0[i].low)
                  rates[index].low=r0[i].low;
               if(rates[index].high < r0[i].high)
                  rates[index].high=r0[i].high;
              }
            rates[index].close=r0[i].close;
           }
      //--- specifying closing time of the next bar in the loop
      tC=tO-PeriodSeconds(base_period);
      //
      cnt++;
     }
   if(cnt<len)
     {
      //-- less data than required, move to the beginning of the buffer
      int d=len-cnt;
      for(int j=0; j<cnt; j++)
         rates[j]=rates[j+d];
      for(int j=cnt;j<len;j++)
        {
         //--- fill unused array elements with zeros
         rates[j].close=0;
         rates[j].open=0;
         rates[j].high=0;
         rates[j].low=0;
         rates[j].time=0;
        }
     }
   shift = sh;  
   return(cnt);
  }

-->

중요한 점이 몇 가지 있는데요.

해당 함수는 틱 볼륨을 반환하지 않습니다. DSC 모드의 함수는 바 오픈시의 볼륨과 동일한 볼륨을 절대로 반환하지 않기 때문입니다. 어렵지 않죠. EA가 새로운 바 형성 시그널과 동일한 틱 볼륨을 이용하는 경우 해당 시그널을 수신할 수 없게 됩니다. 이동 평균 EA에서 동일한 메소드가 적용됩니다. 함수가 틱 볼륨을 카운트하도록 할 수 있지만 제대로 작동하지 않을 겁니다. 혼동을 피하기 위해 저는 틱 볼륨을 아예 계산하지 않습니다.
이 함수는 요청된 막대 수를 반환하지만 첫 번째 막대와 마지막 막대 사이의 시간이 소스 차트의 해당 시간 간격에 비례한다는 의미는 아닙니다. 기록 데이터의 연속적인 부분에 서신이 있을 것입니다. 특정 세그먼트에 주말이 포함되는 경우 그 경계선에 '유령 바'가 나타날 수 있습니다.

다음 그림은 '유령 바'의 예입니다. 10월 7일 00:01에 형성되었는데 10월 26일 23:01에 함께 포함되어 버린 경우죠. 이러한 막대 이후에는 지표의 차트가 소스 차트와 관련하여 왼쪽으로 이동한다는 점에 유의해야 합니다. 초기 시간에 해당하는 시간을 갖는 바는 다른 인덱스를 갖게 됩니다(예: 21:00->21:01).

유령 바

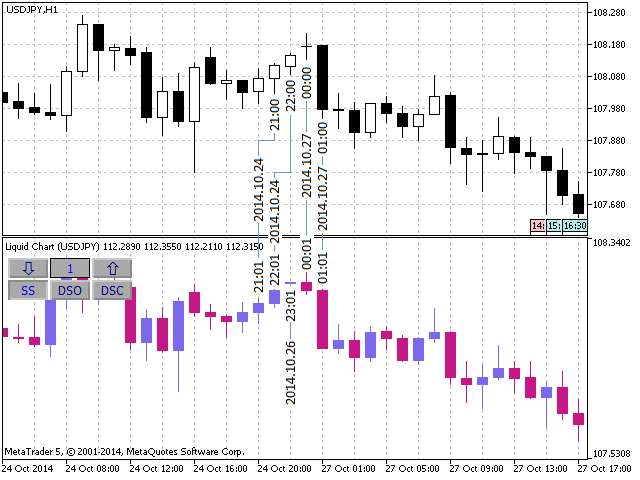
그림 4. 2014년 10월 26일 23:01 유령 바

3. 인디케이터 구현

'리퀴드 차트'를 별도의 창에 나타내는 인디케이터를 작성해 봅시다. 해당 인디케이터는 위의 세 가지 모드 전부에서 작동할 겁니다. 또한 인디케이터 매개 변수 대화창을 따로 호출하지 않고도 모드를 변경하거나 시프트 값을 변경할 수 있도록 만들 겁니다.

liquidchart.mqh 파일의 GetRatesLC() 함수를 이용하겠습니다. RefreshBuffers() 함수에서 호출할 건데요. 이 함수는 OnCalculate 함수에서 호출합니다. OnChartEvent에서도 호출할 수 있습니다. 모드나 시프트를 약간 수정하거나 인디케이터 버퍼를 다시 계산해야 할 수도 있지만요. OnChartEvent 함수가 버튼 활성화와 시프트 값 및 모드 변경을 담당합니다.

인디케이터 입력 매개 변수는 다음과 같습니다.

input ENUM_TIMEFRAMES   BaseTF=PERIOD_M1;       // LC Base Period
input int               Depth=100;              // Depth, bars
input ENUM_LC_MODE      inp_LC_mode=LC_MODE_SS; // LC mode
input int               inp_LC_shift=0;         // LC shift

-->

Depth는 결과 차트 내 바의 개수이며 ENUM_LC_MODE는 인디케이터 플로팅 모드를 나타냅니다.

enum ENUM_LC_MODE
  {//plotting mode
   LC_MODE_SS=0,  // Static Shift
   LC_MODE_DSO=1, // Dynamic Shift, just Open
   LC_MODE_DSC=2  // Dynamic Shift, expected Close
  };

--> inp_LC_mode와 inp_LC_shift 매개 변수는 각각 LC_mode와 LC_shift로 중복됩니다. 버튼을 누르면 그 값을 변경할 수 있죠. 버튼을 만들고 누르는 방법은 본문에서 다루지 않을 겁니다. RefreshBuffers() 함수를 자세히 살펴보겠습니다.

bool RefreshBuffers(int total,
                    double &buff1[],
                    double &buff2[],
                    double &buff3[],
                    double &buff4[],
                    double &col_buffer[])
  {
   MqlRates rates[];
   ArrayResize(rates,Depth);
//---
   int copied=0;
   int shift=0;
   if(LC_mode==LC_MODE_SS)
      shift = LC_shift; //static shift
   else if(LC_mode==LC_MODE_DSO)
      shift = -1;       //calculate shift (beginning of the bar formation)
   else if(LC_mode==LC_MODE_DSC)
      shift = -2;       //calculate shift (end of the bar formation)
   else
      return(false);
//---
   copied=GetRatesLC(0,Depth,rates,BaseTF,shift);
//---
   if(copied<=0)
     {
      Print("No data");
      return(false);
     }
   LC_shift = shift;
   refr_keys();
//--- initialize buffers with empty values
   ArrayInitialize(buff1,0.0);
   ArrayInitialize(buff2,0.0);
   ArrayInitialize(buff3,0.0);
   ArrayInitialize(buff4,0.0);
//---
   int buffer_index=total-copied;
   for(int i=0;i<copied;i++)
     {
      buff1[buffer_index]=rates[i].open;
      buff2[buffer_index]=rates[i].high;
      buff3[buffer_index]=rates[i].low;
      buff4[buffer_index]=rates[i].close;
      //---
      if(rates[i].open<=rates[i].close)
         col_buffer[buffer_index]=1;//bullish or doji
      else
         col_buffer[buffer_index]=0;//bearish
      //
      buffer_index++;
     }
//
   return(true);
  }

-->

실행 모드에 따라 shift 변수 값이 GetRatesLC() 함수로 전달됩니다. 정적 모드의 경우 LC_shift 매개 변수 사본이 될 것이고 개장 또는 폐장 모드에서는 -1 또는 -2 값을 갖게 될 겁니다. 함수를 실행하고 나면 GetRatesLC()는 현재 시프트 값을 shift 변수로 반환합니다. 다시 계산되거나 원래 값 그대로이죠. 해당 값을 LC_shift 변수에 지정하고 refr_keys() 함수를 이용해 그래픽 엘리먼트를 다시 그립니다.

그 후 OHLC 값과 인디케이터 버퍼 내 바 색깔을 새로고침합니다.

인디케이터 전체 코드는 liquid_chart.mq5 파일에 포함되어 있습니다. 해당 인디케이터를 실행하면 다음과 같은 모습으로 나타납니다.

시프트가 0인 리퀴드 차트 인디케이터

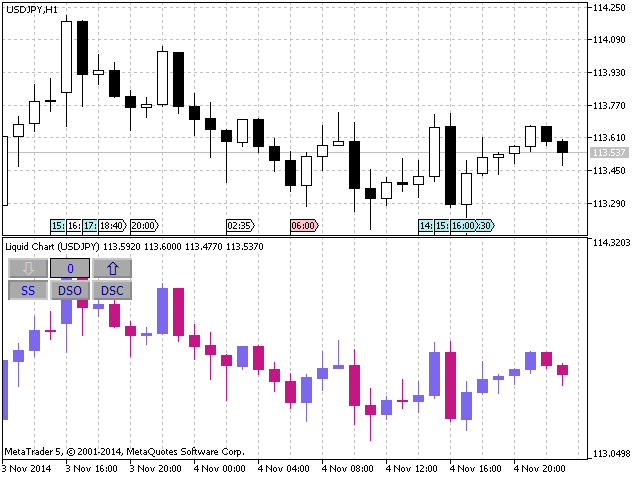
그림 5. 리퀴드 차트 인디케이터

몇 가지 설명을 할게요.

SS 버튼은 인디케이터를 정적 시프트 모드로 변환합니다. 해당 모드에서는 화살표 버튼을 이용해 필요한 시프트 값을 설정할 수 있습니다.
DSO 버튼은 인디케이터를 동적 시프트 모드의 바 형성 시작 부분으로 전환합니다. 해당 모드에서 시프트 값은 자동으로 계산되며 수동으로 수정할 수 없습니다.
DSC 버튼은 인디케이터를 동적 시프트 모드의 바 형성 완료 부분으로 전환합니다. 해당 모드에서도 마찬가지로 수동으로 시프트 값을 수정할 수 없습니다.

SS 모드에서 시프트 값이 0인 경우 인디케이터는 초기 차트 값을 그대로 나타냅니다. 시프트 값을 변경하면 차트가 다시 그려집니다. 28 정도만 되어도 벌써 큰 차이가 보이죠. 약한 '레일'보다 뚜렷한 '망치' 패턴이 보입니다. 매수할 때일까요?

시프트가 28인 리퀴드 차트 인디케이터

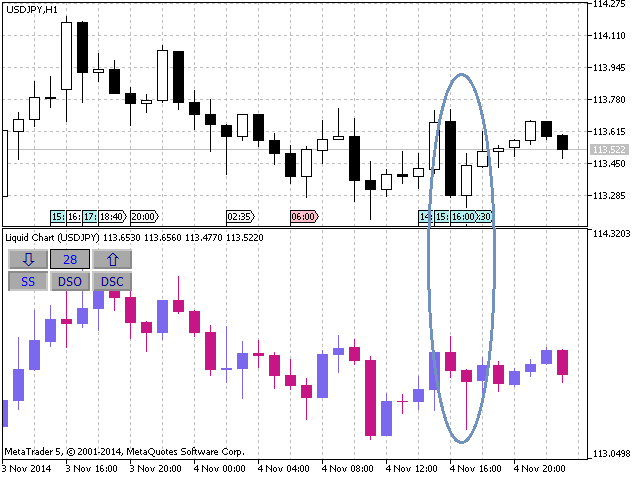
그림 6. 정적 시프트가 28인 리퀴드 차트 인디케이터

인디케이터를 DSO 모드로 전환하면 새로 형성된 바가 항상 오른쪽에 나타날 겁니다. DSC 모드의 경우 기본 타임프레임 값 내에 바가 닫히게 됩니다.

4. 엑스퍼트 어드바이저 생성하기

두 개의 엑스퍼트 어드바이저를 만들어 보겠습니다. 첫 번재 EA는 MA를 이용해 거래하고 두 번째 EA는 '핀 바' 패턴을 이용합니다.

기본 예제 폴더(Experts\Examples\Moving Average)의 이동 평균 EA를 이용하겠습니다. 이렇게 하면 두 개의 완전히 다른 전략에서 정적 또는 동적 시프트의 사용이 어떤 의미가 있는지 알 수 있을 겁니다.

4.1. 이동 평균을 이용하는 EA

우선 인풋 변수를 정의해야 합니다. 네 가지 인풋 변수가 있는데요.

input double MaximumRisk    = 0.1;  // Maximum Risk in percentage
input double DecreaseFactor = 3;    // Decrease factor
input int    MovingPeriod   = 12;   // Moving Average period
input int    MovingShift    = 6;    // Moving Average shift

-->

현대화를 거친 후 세 개의 변수가 추가됩니다.

input ENUM_TIMEFRAMES  BaseTF=PERIOD_M1;  // LC Base Period
input bool             LC_on = true;      // LC mode ON
input int              LC_shift = 0;      // LC shift

-->

LC_on 매개 변수를 이용해 GetRatesLC()가 제대로 작동하는지 확인할 수 있습니다. (LC_on == true && LC_shift == 0)는 (LC_on == false)와 동일한 결과를 가져야 합니다.

시프트를 갖는 MA EA의 현대화에는 liquidchart.mqh 파일이 필요합니다. 시프트 기능이 활성화된 경우 CopyRates() 함수는 GetRatesLC() 함수로 대체됩니다(입력 매개 변수 LC_on이 참인 경우).

   int copied;
   if(LC_on==true)
     {
      int shift = LC_shift;
      copied=GetRatesLC(0,2,rt,BaseTF,shift);
     }
   else
      copied = CopyRates(_Symbol,_Period,0,2,rt);
   if(copied!=2)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }

-->

CheckForOpen() 함수와 CheckForClose() 함수도 마찬가지입니다. 인디케이터 핸들 사용은 지양하고 MA는 수동으로 계산할 겁니다. CopyMABuffer() 함수를 추가합니다.

int CopyMABuffer(int len,double &ma[])
  {
   if(len<=0)
      return(0);
   MqlRates rates[];
   int l=len-1+MovingPeriod;
   int copied;
   if(LC_on==true)
     {
      int shift = LC_shift;
      ArrayResize(rates,l);
      copied=GetRatesLC(MovingShift,l,rates,BaseTF,shift);
     }
   else
      copied=CopyRates(_Symbol,_Period,MovingShift,l,rates);
//      
   if(copied<l)
      return(0);
//
   for(int i=0;i<len;i++)
     {
      double sum=0;
      for(int j=0;j<MovingPeriod;j++)
        {
         if(LC_on==true)
            sum+=rates[j+i].close;
         else
            sum+=rates[copied-1-j-i].close;
        }
      ma[i]=sum/MovingPeriod;
     }
   return(len);
  }

-->

해당 함수는 ma[] 버퍼로 획득 값의 개수 또는 획득에 실패한 경우 0을 반환합니다.

바의 오픈을 어떻게 컨트롤할 것이냐도 잘 생각해 보아야 합니다. 기존의 이동 평균 EA에서는 틱 값을 이용해 구현했습니다.

   if(rt[1].tick_volume>1)
      return;

-->

이 경우는 틱 볼륨이 없으므로 newbar() 함수를 작성해 보겠습니다.

bool newbar(datetime t)
  {
   static datetime t_prev=0;
   if(t!=t_prev)
     {
      t_prev=t;
      return(true);
     }
   return(false);
  }

-->

작동 원리는 바의 오픈 시간을 직전 값과 비교하는 것입니다. CheckForOpen() 함수와 CheckForClose() 함수의 틱 볼륨 확인을 newbar() 함수 호출로 바꿉니다.

   if(newbar(rt[1].time)==false)
      return;

-->

전체 코드와 EA는 moving_average_lc.mq5 파일에 포함되어 있습니다.

4.2. '핀 바' 패턴을 이용하는 EA

핀 바 또는 피노키오 바는 세 개의 바로 구성되는 패턴입니다. 가운데에 위치한 바가 긴 그림자 또는 '코'를 갖는데요. 이는 가격 움직임의 전환 가능성을 나타냅니다. 양쪽에 위치한 바는 '눈'이라고 불립니다. 이 두 개 바의 극단값은 가운데 바의 그림자 밖으로 나오지 않습니다. 캔들스틱 모델을 이용하는 투자자들이 이 핀 바 패턴을 참 좋아합니다.

우리 예제의 핀 바는 다음의 가격 하락 반전 조건을 만족해야 합니다.

r[0] 바는 불리쉬해야 합니다.
r[2] 바는 베어리쉬해야 하죠.
A와 C 가격의 최대값은 B의 값보다 클 수 없습니다. A와 C는 각각 r[0]와 r[2] 바의 High 값이 됩니다. B는 r[1] 바의High 값입니다.
가운데 바는 r[1] 바의 Open과 Close 사이의 차이를 나타내는 모듈이며(OC) 외부 변수로 설정된 포인트 개수를 초과해서는 안됩니다.
가운데 바의 그림자, 또는 r[1] 바의 High 값과 Open 및 Close의 최대값 사이의 차이는 외부 변수로 설정된 포인트 개수 미만이어서는 안됩니다.
가운데 바의 그림자와 바디의 비율은 외부 변수로 설정된 값보다 작아서는 안됩니다.

r[3] 바가 오픈될 때 패턴 확인이 진행됩니다.

핀 바

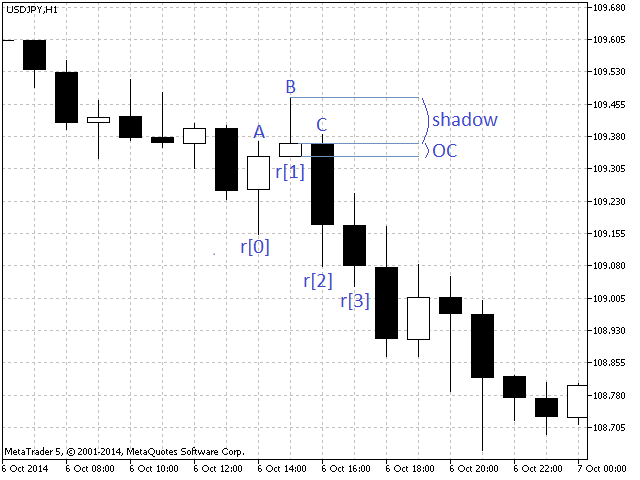
그림 7. '핀 바' 패턴

가격 하락 반전을 나타내는 핀 바 패턴을 찾는 코드는 다음과 같습니다.

   if(r[0].open<r[0].close && r[2].open>r[2].close && r[1].high>MathMax(r[0].high,r[2].high))
     {
     //--- eyes of the upper pin bar
      double oc=MathAbs(r[1].open-r[1].close)/_Point;
      if(oc>inp_pb_max_OC)
         return(0);
      double shdw=(r[1].high-MathMax(r[1].open,r[1].close))/_Point;
      if(shdw<inp_pb_min_shdw)
         return(0);
      if(oc!=0)
        {
         if((shdw/oc)<inp_pb_min_ratio)
            return(0);
        }
      return(1);
     }

-->

가격 상승 반전의 경우도 마찬가지이죠. 따라서 핀 바 패턴의 존재 여부를 확인하는 함수는 다음과 같죠.

int IsPinbar(MqlRates &r[])
  {
   //--- there must be 4 values in the r[] array
   if(ArraySize(r)<4)
      return(0);
   if(r[0].open<r[0].close && r[2].open>r[2].close && r[1].high>MathMax(r[0].high,r[2].high))
     {
      //--- eyes of the upper pin bar
      double oc=MathAbs(r[1].open-r[1].close)/_Point;
      if(oc>inp_pb_max_OC)
         return(0);
      double shdw=(r[1].high-MathMax(r[1].open,r[1].close))/_Point;
      if(shdw<inp_pb_min_shdw)
         return(0);
      if(oc!=0)
        {
         if((shdw/oc)<inp_pb_min_ratio)
            return(0);
        }
      return(1);
     }
   else if(r[0].open>r[0].close && r[2].open<r[2].close && r[1].low<MathMin(r[0].low,r[2].low))
     {
      //--- eyes of the lower pin bar
      double oc=MathAbs(r[1].open-r[1].close)/_Point;
      if(oc>inp_pb_max_OC)
         return(0);
      double shdw=(MathMin(r[1].open,r[1].close)-r[1].low)/_Point;
      if(shdw<inp_pb_min_shdw)
         return(0);
      if(oc!=0)
        {
         if((shdw/oc)<inp_pb_min_ratio)
            return(0);
        }
      return(-1);
     }
   return(0);
  }

-->

전달된 기록 배열은 최소 4개의 엘리먼트를 가져야 합니다. 상위 핀 바가 탐지된 경우(가격 하락 반전) 해당 함수는 1을 반환합니다. 하위 핀 바가 탐지된 경우(가격 상승 반전) 해당 함수는 -1을 반환하죠. 핀 바가 나타나지 않는 경우 0을 반환합니다. 해당 함수는 다음의 입력 매개 변수를 이용합니다.

input uint   inp_pb_min_shdw     = 40;    // Pin bar min shadow, point
input uint   inp_pb_max_OC       = 20;    // Pin bar max OC, point
input double inp_pb_min_ratio    = 2.0;   // Pin bar shadow to OC min ratio

-->

핀 바를 적용한 가장 간단한 거래 전략을 이용할 겁니다. 가격 하락 반전이 예상되는 경우 매도하고 상승 반전이 예상되는 경우 매수합니다. 일반적으로 인디케이터를 한번 확인해야 하지만 이 경우 실험의 무결성과는 관련이 없으므로 넘어갑니다. 핀 바만을 사용할 겁니다.

'핀 바' 패턴을 이용하는 EA는 이동 평균을 이용하는 EA를 기반으로 합니다. 후자에서 CopyMABuffer() 함수를 삭제하고 CheckForOpen() 함수와 CheckForClose() 함수에서 해당 함수 호출도 삭제합니다. 필요한 기록 데이터 개수는 두 개에서 네 개로 늘어날 겁니다. r[3] 바의 시간을 이용해 새로운 바 오픈을 확인합니다.

   int copied;
   if(LC_on==true)
   {
      int shift = LC_shift;
      copied=GetRatesLC(0,4,rt,BaseTF,shift);
   }
   else
      copied = CopyRates(_Symbol,_Period,0,4,rt);
   if(copied!=4)
     {
      Print("CopyRates of ",_Symbol," failed, no history");
      return;
     }
   if(newbar(rt[3].time)==false)
      return;

-->

포지션 오픈 신호 확인은 다음과 같이 발생합니다.

   int pb=IsPinbar(rt);
   if(pb==1)       // upper pin bar
      signal=ORDER_TYPE_SELL; // sell conditions
   else if(pb==-1) // lower pin bar
      signal=ORDER_TYPE_BUY;  // buy conditions

-->

반대 핀 바가 나타나는 경우 다음의 방법으로 포지션을 청산합니다.

   if(type==(long)POSITION_TYPE_BUY && pb==1)
      signal=true;
   if(type==(long)POSITION_TYPE_SELL && pb==-1)
      signal=true;

-->

입력 변수를 엄격하게 조절하는 경우 핀 바 패턴은 거의 나타나지 않습니다. 따라서 핀 바만을 이용해 포지션을 청산할 때에는 수익을 잃거나 청산 시 손실이 발생할 위험이 있습니다.

그렇기 때문에 TP와 SL 레벨을 추가합니다. 해당 레벨은 각각 inp_tp_pp와 inp_sl_pp 외부 매개 변수로 설정됩니다.

   double sl=0,tp=0,p=0;
   double ask=SymbolInfoDouble(_Symbol,SYMBOL_ASK);
   double bid=SymbolInfoDouble(_Symbol,SYMBOL_BID);
   if(signal==ORDER_TYPE_SELL)
   {
     p=bid;
     if(inp_sl_pp!=0)
       sl=NormalizeDouble(ask+inp_sl_pp*_Point,_Digits);
     if(inp_tp_pp!=0)
       tp=NormalizeDouble(ask-inp_sl_pp*_Point,_Digits);
   } else {
     p=ask;
     if(inp_sl_pp!=0)
       sl=NormalizeDouble(bid-inp_sl_pp*_Point,_Digits);
     if(inp_tp_pp!=0)
       tp=NormalizeDouble(bid+inp_sl_pp*_Point,_Digits);
   }
   CTrade trade;
   trade.PositionOpen(_Symbol,signal,TradeSizeOptimized(),p,sl,tp);

-->

inp_tp_pp 또는 inp_sl_pp의 값이 0인 경우, TP 또는 SL은 설정되지 않습니다.

수정이 완료되었습니다. EA가 준비되었군요. 전체 코드는 pinbar_lc.mq5 파일에서 찾아볼 수 있습니다.

5. EA 최적화

EA를 최적화하여 시프트 차트의 효율성을 평가해 보겠습니다. 이때 가장 중요한 매개 변수는 수익, 드로우다운, 거래 건수입니다. 이동 평균을 이용한 EA는 인디케이터 전략의 예시로, '핀 바' 패턴을 이용하는 EA는 비인디케이터 전략의 예시로 사용될 겁니다.

MetaQuotes-Demo 서버의 지난 반년 간의 시세를 이용해 최적화하겠습니다. 이번 실험은 EURUSD, GBPUSD, USDJPY을 대상으로 합니다. 초기 예수금은 USD 3000이며 레버리지는 1:100입니다. 테스트 모드에서 'All ticks'를 선택합니다. 최적화 모드는 'fast(일반 알고리즘), Balance Max'입니다.

5.1. 이동 평균 EA 최적화 분석 결과

여러 모드에 대한 최적화 결과를 살펴보겠습니다. 시프트가 0인 경우, 정적 시프트가 있는 경우, 그리고 동적 시프트가 있는 경우(DSO와 DSC)입니다.

해당 테스트는 2014년 4월 1일부터 2014년 10월 25일까지의 EURUSD, GBPUSD, USDJPY를 대상으로 시행되었습니다. 타임프레임은 H1입니다.

EA 입력 매개 변수

매개 변수	값
Maximum Risk in percentage	0.1
Descrease factor	3.0
Moving Average period	12
Moving Average shift	6
BaseTF	1 Minute
LC_on	true
LC_shift	0

표 3. MA LC EA 입력 매개 변수

5.1.1. 시프트 모드 비활성화 시 EA 최적화

최적화된 매개 변수

매개 변수	시작	단계	정지
Moving Average period	12	1	90
Moving Average shift	6	1	30

표 4. 제로 시프트 모드에서 최적화된 MA LC EA 매개 변수

제로 시프트 모드 EA 최적화 그래프, EURUSD

제로 시프트 모드 최적화, EURUSD

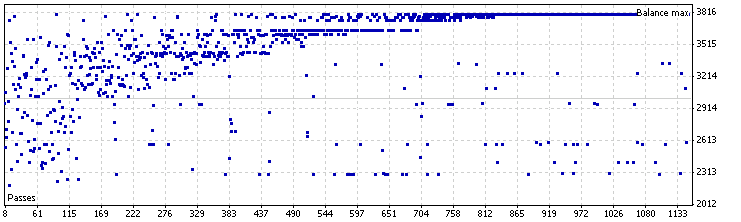
그림 8. 제로 시프트 모드 MA LC EA 최적화, EURUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift
3796,43	796,43	16,18	111	24	12
3776,98	776,98	17,70	77	55	22
3767,45	767,45	16,10	74	59	23
3740,38	740,38	15,87	78	55	17
3641,16	641,16	15,97	105	12	17

표 5. 제로 시프트 모드 EURUSD MA LC EA 최상 최적화 결과

제로 시프트 모드 EA 최적화 그래프, GBPUSD

제로 시프트 모드 최적화, GBPUSD

그림 9. 제로 시프트 모드 MA LC EA 최적화, GBPUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift
4025,75	1025,75	8,08	80	18	22
3857,90	857,90	15,04	74	55	13
3851,40	851,40	18,16	80	13	24
3849,48	849,48	13,05	69	34	29
3804,70	804,70	16,57	137	25	8

표 6. 제로 시프트 모드 GBPUSD MA LC EA 최상 최적화 결과

제로 시프트 모드 EA 최적화 결과, USDJPY

제로 시프트 모드 최적화, USDJPY

그림 10. 제로 시프트 모드 MA LC EA 최적화, USDJPY

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift
5801,63	2801,63	11,54	48	65	23
5789,17	2789,17	14,03	50	44	27
5539,06	2539,06	17,14	46	67	27
5331,34	2331,34	15,05	61	70	9
5045,19	2045,19	12,61	48	83	15

표 7. 제로 시프트 모드 USDJPY MA LC EA 최적화 최상 결과

5.1.2. 동적 시프트 모드 EA 최적화

최적화된 매개 변수

매개 변수	시작	단계	정지
Moving Average period	12	1	90
Moving Average shift	6	1	30
LC_shift	1	1	59

표 8. 정적 시프트 모드에서 최적화된 MA LC EA 매개 변수

정적 시프트 모드 EA 최적화 그래프, EURUSD

정적 시프트 모드 최적화, EURUSD

그림 11. 정적 시프트 모드 MA LC EA 최적화, EURUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift	LC_shift
4385,06	1385,06	12,87	100	32	11	8
4149,63	1149,63	14,22	66	77	25	23
3984,92	984,92	21,52	122	12	11	26
3969,35	969,35	16,08	111	32	11	24
3922,95	922,95	12,29	57	77	25	10

표 9. 정적 시프트 모드 EURUSD MA LC EA 최적화 최상 결과

정적 시프트 모드 EA 최적화 그래프, GBPUSD

정적 시프트 모드 최적화, GBPUSD

그림 12. 정적 시프트 모드 MA LC EA 최적화, GBPUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift	LC_shift
4571,07	1571,07	14,90	79	12	25	42
4488,90	1488,90	15,46	73	12	25	47
4320,31	1320,31	9,59	107	12	16	27
4113,47	1113,47	10,96	75	12	25	15
4069,21	1069,21	15,27	74	12	25	50

표 10. 정적 시프트 모드 GBPUSD MA LC EA 최적화 최상 결과

정적 시프트 모드 EA 최적화 그래프, USDJPY

정적 시프트 모드 최적화, USDJPY

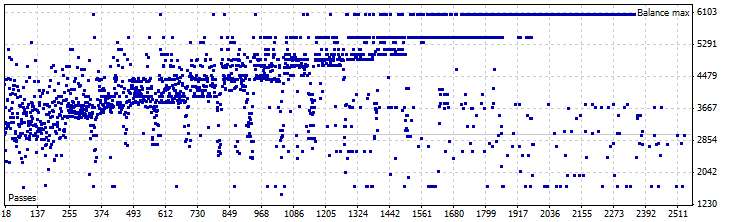
그림 13. 정적 시프트 모드 MA LC EA 최적화, USDJPY

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift	LC_shift
6051,39	3051,39	15,94	53	76	12	31
5448,98	2448,98	10,71	54	44	30	2
5328,15	2328,15	11,90	50	82	13	52
5162,82	2162,82	10,46	71	22	26	24
5154,71	2154,71	14,34	54	75	14	58

표 11. 정적 시프트 모드 USDJPY MA LC EA 최적화 최상 결과

5.1.3. 동적 시프트 모드 EA 최적화

최적화된 매개 변수

매개 변수	시작	단계	정지
Moving Average period	12	1	90
Moving Average shift	6	1	30
LC_shift	-2	1	-1

표 12. 동적 시프트 모드에서 최적화된 MA LC EA 매개 변수

동적 시프트 모드 EA 최적화 그래프, EURUSD

동적 시프트 모드 최적화, EURUSD

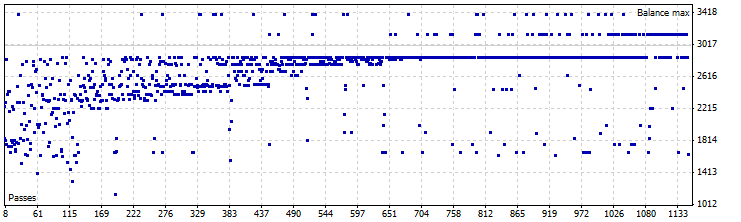
그림 14. 동적 시프트 모드에서 최적화된 MA LC EA

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift	LC_shift
3392,64	392,64	27,95	594	15	13	-2
3140,26	140,26	23,35	514	12	17	-2
2847,12	-152,88	17,04	390	79	23	-1
2847,12	-152,88	17,04	390	79	12	-1
2826,25	-173,75	20,12	350	85	22	-1

표 13. 동적 시프트 모드 EURUSD MA LC EA 최적화 최상 결과

동적 시프트 모드 EA 최적화 그래프, GBPUSD

동적 시프트 모드 최적화, GBPUSD

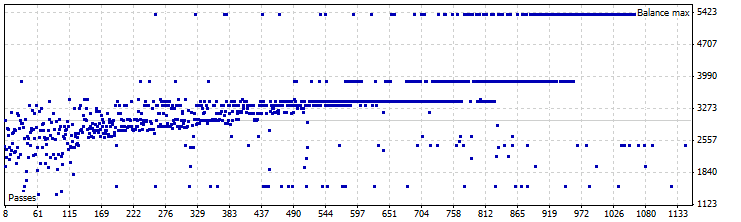
그림 15. 동적 시프트 모드 MA LC EA 최적화, GBPUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift	LC_shift
5377,58	2377,58	19,73	391	12	26	-2
3865,50	865,50	18,18	380	23	23	-2
3465,63	465,63	21,22	329	48	21	-2
3428,99	428,99	24,55	574	51	16	-1
3428,99	428,99	24,55	574	51	15	-1

표 14. 동적 시프트 모드 GBPUSD MA LC EA 최적화 최상 결과

동적 시프트 모드 EA 최적화 그래프, USDJPY

동적 시프트 모드 최적화, USDJPY

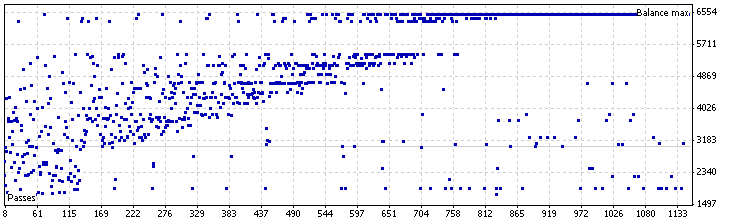
그림 16. 동적 시프트 모드 MA LC EA 최적화, USDJPY

최상의 결과

결과	수익	드로우다운(%)	거래 수	MovingPeriod	MovingShift	LC_shift
6500,19	3500,19	17,45	244	42	28	-2
6374,18	3374,18	19,91	243	54	24	-2
6293,29	3293,29	19,30	235	48	27	-2
5427,69	2427,69	17,65	245	90	8	-2
5421,83	2421,83	16,30	301	59	12	-2

표 15. 동적 시프트 모드 MA LC EA 최적화 최상 결과

5.2. '핀 바' 패턴을 이용한 EA 최적화 결과 분석

여러 모드에 대한 최적화 결과를 살펴보겠습니다. 시프트가 0인 경우, 정적 시프트가 있는 경우, 그리고 동적 시프트가 있는 경우(DSO와 DSC)입니다. 해당 테스트는 2014년 4월 1일에서 2014년 10월 25일까지의 EURUSD, GBPUSD USDJPY를 대상으로 시행할 겁니다. 타임프레임은 H1입니다.

EA 입력 매개 변수

매개 변수	값
Maximum Risk in percentage	0.1
Decrease factor	3.0
Pin bar min shadow, points	40
Pin bar max OC, points	110
Pin bar shadow to OC min ratio	1.4
SL, points(0: OFF)	150
TP, points(0: OFF)	300
LC Base Period	1 Minute
LC mode ON	true
LC shift	0

표 16. 핀 바 LC EA 입력 매개 변수

핀 바의 형태를 결정하는 매개 변수를 최적화할 겁니다. '코'의 길이, '코'의 길이와 가운데 바 바디 길이 비율, 그리고 최대 바디 크기를 결정하는 변수들이죠. TP 및 SL 레벨도 최적화하겠습니다.

5.2.1. 시프트 모드 비활성화 시 EA 최적화

최적화된 매개 변수

매개 변수	시작	단계	정지
Pin bar min shadow, points	100	20	400
Pin bar max OC, points	20	20	100
Pin bar shadow to OC min ratio	1	0.2	3
SL, points(0: OFF)	150	50	500
TP, points(0: OFF)	150	50	500

표 17. 제로 시프트 모드에서 최적화된 Pin Bar LC EA 매개 변수

제로 시프트 모드 EA 최적화 그래프, EURUSD

제로 시프트 모드 최적화, EURUSD

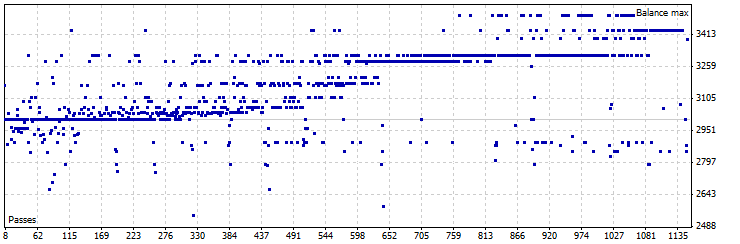
그림 17. 제로 시프트 모드 Pin Bar LC EA 최적화, EURUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP
3504,59	504,59	9,82	33	100	60	1.8	450	500
3428,89	428,89	8,72	21	120	60	2.8	450	350
3392,37	392,37	9,94	30	100	60	2,6	450	250
3388,54	388,54	9,93	31	100	80	2,2	450	300
3311,84	311,84	6,84	13	140	60	2,2	300	450

표 18. 제로 시프트 모드 EURUSD Pin Bar LC EA 최적화 최상 결과

제로 시프트 모드 EA 최적화 그래프, GBPUSD

제로 시프트 모드 최적화, GBPUSD

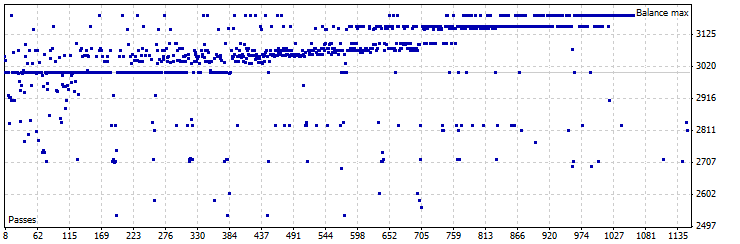
그림 18. 제로 시프트 모드 Pin Bar LC EA 최적화, GBPUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP
3187,13	187,13	11,10	13	160	60	2,6	500	350
3148,73	148,73	3,23	4	220	40	2,8	400	400
3142,67	142,67	11,27	17	160	100	1,8	500	350
3140,80	140,80	11,79	13	180	100	2	500	500
3094,20	94,20	1,62	1	260	60	1,6	500	400

표 19. 제로 시프트 모드 GBPUSD Pin Bar LC EA 최적화 최상 결과

제로 시프트 모드 EA 최적화 결과, USDJPY

시프트 모드 비활성화 최적화, USDJPY

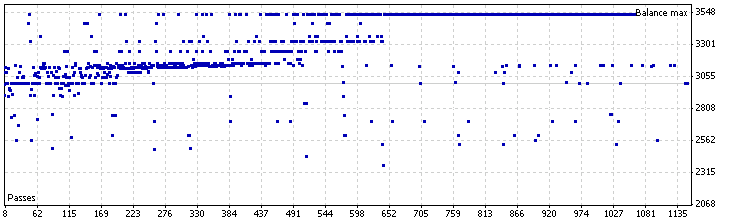
그림 19. 제로 시프트 모드 Pin Bar LC EA 최적화, USDJPY

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP
3531,99	531,99	9,00	6	160	60	2.2	450	500
3355,91	355,91	18,25	16	120	60	1,6	450	400
3241,93	241,93	9,11	4	160	40	2,8	450	500
3180,43	180,43	6,05	33	100	80	1,8	150	450
3152,97	152,97	3,14	6	160	80	2,8	150	500

표 20. 제로 시프트 모드 USDJPY Pin Bar LC EA 최적화 최상 결과

5.2.2. 동적 시프트 모드 EA 최적화

최적화된 매개 변수

매개 변수	시작	단계	정지
Pin bar min shadow, points	100	20	400
Pin bar max OC, points	20	20	100
Pin bar shadow to OC min ratio	1	0.2	3
SL, points(0: OFF)	150	50	500
TP, points(0: OFF)	150	50	500
LC shift	1	1	59

표 21. 정적 시프트 모드에서 최적화된 Pin Bar LC EA 매개 변수

정적 시프트 모드 EA 최적화 그래프, EURUSD

정적 시프트 모드 최적화, EURUSD

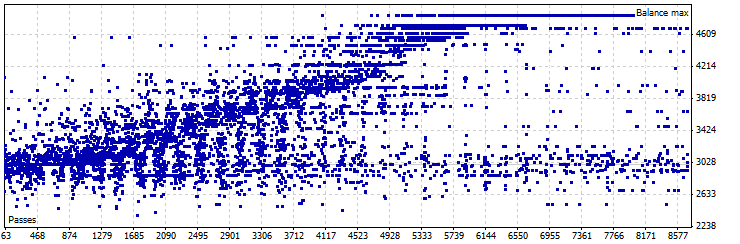
그림 20. 정적 시프트 모드 Pin Bar LC EA 최적화, EURUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP	LC shift
4843,54	1843,54	10,14	19	120	80	1,6	500	500	23
4714,81	1714,81	10,99	28	100	100	1,6	500	500	23
4672,12	1672,12	10,16	18	120	80	1,8	500	500	23
4610,13	1610,13	9,43	19	120	80	1,6	450	450	23
4562,21	1562,21	13,94	27	100	100	1,6	500	400	25

표 22. 정적 시프트 모드 EURUSD Pin Bar LC EA 최적화 최상 결과

정적 시프트 모드 EA 최적화 그래프, GBPUSD

정적 시프트 모드 최적화, GBPUSD

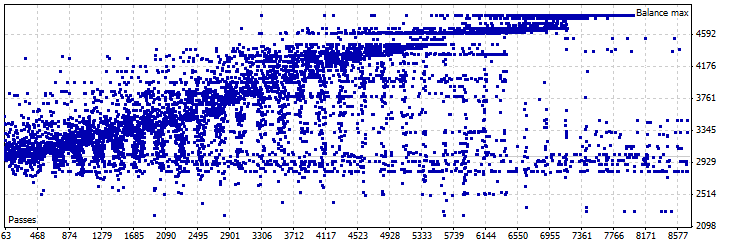
그림 21. 정적 시프트 모드 Pin Bar LC EA 최적화, GBPUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP	LC shift
4838,10	1838,10	5,60	34	100	40	2,4	450	500	24
4797,09	1797,09	5,43	35	100	40	2,6	400	500	24
4755,57	1755,57	7,36	42	100	100	2	400	500	24
4725,41	1725,41	8,35	45	100	80	1	400	500	24
4705,61	1705,61	8,32	41	100	100	2	450	500	24

표 23. 정적 시프트 모드 GBPUSD Pin Bar LC EA 최적화 최상 결과

정적 시프트 모드 EA 최적화 그래프, USDJPY

정적 시프트 모드 최적화, USDJPY

그림 22. 정적 시프트 모드 Pin Bar LC EA 최적화, USDJPY

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP	LC shift
4108,83	1108,83	6,45	9	140	40	1,4	500	450	55
3966,74	966,74	7,88	12	140	60	2,8	450	500	45
3955,32	955,32	9,91	21	120	80	2	500	500	45
3953,80	953,80	6,13	10	140	60	2,8	450	450	47
3944,33	944,33	6,42	6	160	100	2,6	500	400	44

표 24. 정적 시프트 모드 USDJPY Pin Bar LC EA 최적화 최상 결과

5.2.3. 동적 시프트 모드 EA 최적화

최적화된 매개 변수

매개 변수	시작	단계	정지
Pin bar min shadow, points	100	20	400
Pin bar max OC, points	20	20	100
Pin bar shadow to OC min ratio	1	0.2	3
SL, points(0: OFF)	150	50	500
TP, points(0: OFF)	150	50	500
LC shift	-2	1	-1

표 25. 동적 시프트 모드에서 최적화된 Pin Bar LC EA 매개 변수

동적 시프트 모드 EA 최적화 그래프, EURUSD

동적 시프트 모드 최적화, EURUSD

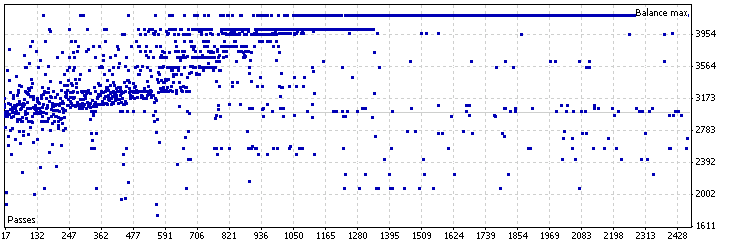
그림 23. 동적 시프트 모드 Pin Bar LC EA 최적화, EUR USD

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP	LC shift
4185,65	1185,65	13,22	49	200	100	1,8	450	500	-2
4011,80	1011,80	13,75	49	200	100	2	400	500	-2
3989,28	989,28	12,01	76	140	20	1,2	350	200	-1
3979,50	979,50	16,45	157	100	20	1	450	500	-1
3957,25	957,25	16,68	162	100	20	1	400	500	-1

표 26. 정적 시프트 모드 EURUSD Pin Bar LC EA 최적화 최상 결과

동적 시프트 모드 EA 최적화 그래프, GBPUSD

동적 시프트 모드 최적화, GBPUSD

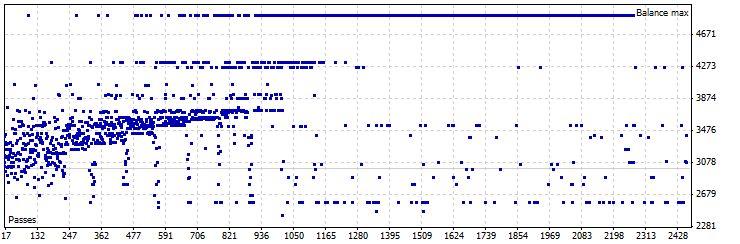
그림 24. 동적 시프트 모드 Pin Bar LC EA 최적화, GBPUSD

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP	LC shift
4906,84	1906,84	10,10	179	120	40	1,8	500	500	-2
4316,46	1316,46	10,71	151	120	20	2,4	450	500	-1
4250,96	1250,96	12,40	174	120	40	1,8	500	500	-1
4040,82	1040,82	12,40	194	120	60	2	500	200	-2
4032,85	1032,85	11,70	139	140	40	2	400	200	-1

표 27. 동적 시프트 모드 GBPUSD Pin Bar LC EA 최적화 최상 결과

동적 시프트 모드 EA 최적화 그래프, USDJPY

동적 시프트 모드 최적화, USDJPY

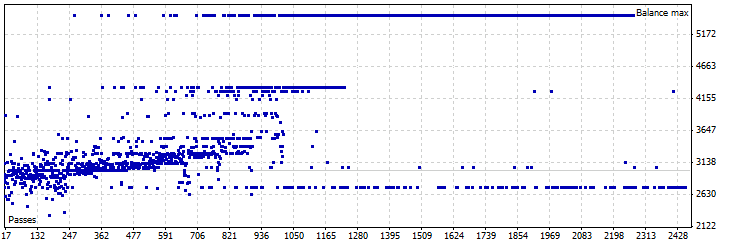
그림 25. 동적 시프트 모드 Pin Bar LC EA 최적화, USDJPY

최상의 결과

결과	수익	드로우다운(%)	거래 수	Pin Bar 최소 그림자	Pin Bar 최대 OC	Pin Bar 그림자 -OC 최소 비율	SL	TP	LC shift
5472,67	2472,67	13,01	138	100	20	2,4	500	500	-1
4319,84	1319,84	15,87	146	100	20	2,2	400	500	-1
4259,54	1259,54	19,71	137	100	20	2,4	500	500	-2
4197,57	1197,57	15,98	152	100	20	1	350	500	-1
3908,19	908,19	16,79	110	120	40	3	400	400	-1

표 28. 동적 시프트 모드 USDJPY Pin Bar LC EA 최적화 최상 결과

6. 최적화 결과 비교

비교 표를 만들겠습니다. 최상의 결과가 나타난 표의 수익, 드로우다운 및 거래 건수의 최대값을 모두 선택하겠습니다. 정적 또는 동적 시프트 모드에서 획득한 값 옆에 제로 시프트 모드의 값과 비교한 변화(%)를 적어 넣겠습니다.

6.1. 이동 평균을 이용하는 EA

수익

	제로 시프트	정적 시프트	동적 시프트
EURUSD	796,43	1385,06 (+74%)	392,64 (-51%)
GBPUSD	1025,75	1571,07 (+53%)	2377,58 (+132%)
USDJPY	2801,63	3051,39 (+9%)	3500,19 (+25%)

표 29. MA LC EA 최적화 최고 결과표 최대 수익값 비교

드로우다운

	제로 시프트	정적 시프트	동적 시프트
EURUSD	17,7	21,52 (+22%)	27,95 (+58%)
GBPUSD	18,16	15,46 (-15%)	24,55 (+35%)
USDJPY	17,14	15,94 (-7%)	19,91 (+16%)

표 30. MA LC EA 최적화 최고 결과표 최대 드로우다운값 비교

거래 건수

	제로 시프트	정적 시프트	동적 시프트
EURUSD	111	122 (+10%)	594 (+435%)
GBPUSD	137	107 (-22%)	574 (+319%)
USDJPY	61	71 (+16%)	301 (+393%)

표 31. MA LC EA 최적화 최고 결과표 최대 거래 건수 비교

동적 시프트 모드에서 진입 시점의 개수가 크게 늘어난 것이 눈에 띕니다. 하지만 드로우다운 또한 상당히 증가했으며 EURUSD의 경우 수익은 두 배로 줄었습니다.

해당 EA의 경우 정적 시프트 모드를 이용했을 때의 수익성이 더 좋네요. GBPUSD와 USDJPY의 경우 드로우다운이 감소했고 EURUSD와 GBPUSD의 경우 수익이 크게 증가했습니다.

6.2. '핀 바' 패턴을 이용하는 EA

수익

	제로 시프트	정적 시프트	동적 시프트
EURUSD	504,59	1843,54 (+265%)	1185,65 (+135%)
GBPUSD	187,13	1838,10 (+882%)	1906,84 (+919%)
USDJPY	531,99	1108,83 (+108%)	2472,67 (+365%)

표 32. Pin Bar LC EA 최적화 최고 결과표 최대 수익값 비교

드로우다운

	제로 시프트	정적 시프트	동적 시프트
EURUSD	9,94	13,94 (+40%)	16,68 (+68%)
GBPUSD	11,79	8,35 (-29%)	12,4 (+5%)
USDJPY	18,25	9,91 (-46%)	19,71 (+8%)

표 33. Pin Bar LC EA 최적화 최고 결과표 최대 드로우다운 비교

거래 건수

	제로 시프트	정적 시프트	동적 시프트
EURUSD	33	28 (-15%)	162 (+391%)
GBPUSD	17	45 (+165%)	194 (+1041%)
USDJPY	33	21 (-36%)	152 (+361%)

표 34. Pin Bar LC EA 최적화 최고 결과표 최대 거래 건수 비교

동적 시프트 모드의 경우 다시 한번 거래 건수가 크게 증가했습니다. 하지만 드로우다운의 엄청난 증가는 EURUSD 통화쌍의 경우에만 발생했습니다. 다른 통화쌍의 경우 약 5~8% 정도의 드로우다운만이 발생했습니다.

동적 시프트 모드에서는 최적화 결과 GBPUSD와 USDJPY의 수익이 제한적으로 나타났습니다. 그래도 해당 통화쌍에 대한 눈에 띄는 드로우다운 감소가 있었습니다. EURUSD의 경우 증가했죠. 해당 EA의 경우 정적 시프트 모드 사용 시 수익성이 떨어지는 것 같군요.

결론

'리퀴드 차트'의 플로팅 원칙을 알아보고 인디케이터를 사용하거나 사용하지 않는 EA의 최적화 결과에 대한 해당 차트의 영향을 확인해 봤습니다.

다음의 결론이 나옵니다.

인디케이터 전략을 이용하는 EA의 경우 정적 시프트 모드가 더 잘 맞습니다. 보다 정확한 시장 진입 지점을 알 수 있으므로 드로우다운이 감소하고 수익이 증가하죠.
패턴을 이용하는 EA의 경우 동적 시프트 모드가 더 적절합니다. 드로우다운이 증가하긴 하지만 동시에 진입 지점도 더 많아지죠.
동적 시프트 모드를 훌륭한 자금 관리 시스템과 함께 이용하는 경우 뛰어난 결과를 가져올 수 있습니다.
인디케이터 전략에 적합해 보이기는 하지만 정적 시프트 모드에는 한 가지 큰 단점이 있습니다. 최적의 결과를 낳는 시프트 값이 다른 입력 변수 목록의 변수라는 건데요. 우선 이 목록을 제대로 맞추는 게 문제이기 때문이죠.

MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/1208

파일 첨부됨 |

ZIP파일 다운로드

liquid_chart.mq5 (27.15 KB)

moving_average_lc.mq5 (16.98 KB)

pinbar_lc.mq5 (18.61 KB)

liquidchart.mqh (8.32 KB)

경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.

이 작가의 다른 글

MQL5 Expert Advisor의 GSM 모뎀 작업

토론으로 가기

MQL5 프로그래밍 기초: 터미널 글로벌 변수

이 문서에서는 터미널에서 글로벌 변수 작업을 용이하게 하는 객체 생성을 위한 MQL5 언어의 객체 지향 기능에 중점을 두고 알아보겠습니다. 실전적인 예를 들어보자면, 글로벌 변수가 프로그램 단계 구현을 위한 제어점으로 사용되는 경우를 고려합니다.

MQL4, MQL5로 프랙탈을 이용한 추세선 그리기

이번 글에서는 MQL4와 MQL5로 프랙탈 인디케이터를 기반으로 하는 자동 추세선 플로팅에 관한 내용을 다룹니다. 두 언어의 솔루션을 서로 비교할 수 있도록 작성되었습니다. 추세선은 가장 마지막으로 생성된 두 개의 프랙탈을 기반으로 플로팅됩니다.

트레이더의 통계 도우미: 가설들

이 문서에서는 수리통계학의 기초 중 하나인 가설에 대해 다뤄보겠습니다. 다양한 가설들은 실제 예시에 수리통계적 관점으로 접근해서 검토, 검증됩니다. 실제 데이터는 비모수적 방법을 사용하여 일반화됩니다. 데이터 처리에는 Statistica 패키지와 포팅된 ALGLIB MQL5 수리분석 라이브러리가 사용됩니다.

MQL5 쿡북: BookEvent 핸들링

이번 글은 시장 심도 이벤트와 그 원리 및 프로세스를 다룹니다. 시장 심도를 다루는 MQL 프로그램을 예로 들겠습니다. 해당 프로그램은 객체 지향 접근법을 적용해 작성되었습니다. 핸들링 결과는 화면에 패널 및 시장 심도 레벨로 표시됩니다.