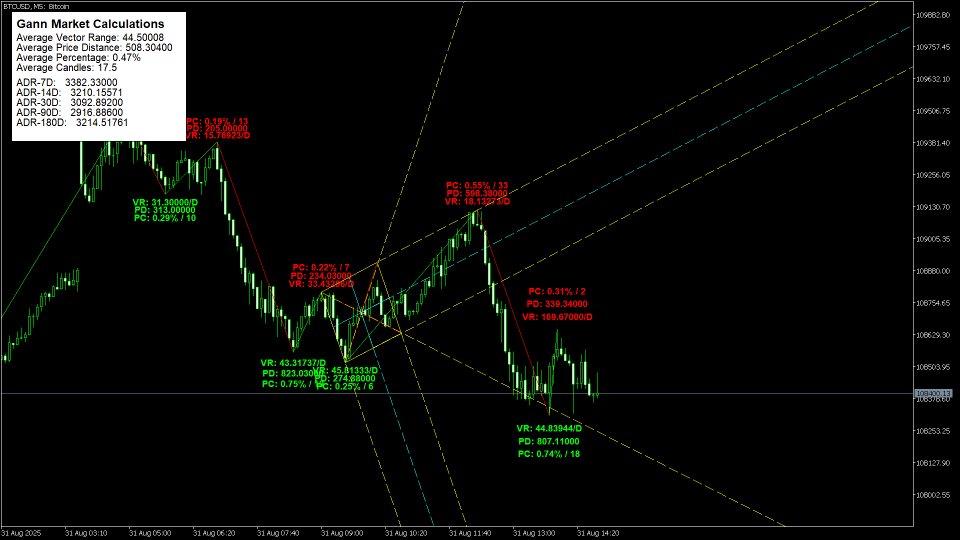
Gann Swing Calculations Methods

Introducción

William Delbert Gann (1878-1955) es uno de los operadores más enigmáticos y exitosos de la historia financiera, ya que desarrolló un sofisticado marco matemático que combinaba geometría, astronomía y leyes naturales para predecir los movimientos del mercado. Su teoría se basaba en formas geométricas naturales y matemáticas antiguas. La teoría de Gann afirma que los patrones y ángulos de un activo en el mercado pueden servir para predecir los movimientos futuros del precio.

Un elemento central de la metodología de Gann era su enfoque del swing trading, un método sistemático para identificar los puntos de inflexión del mercado mediante cálculos matemáticos que eliminaban el "ruido" del mercado y revelaban la estructura geométrica subyacente de los movimientos de los precios.

La base del marco matemático de Gann

Filosofía básica y teoría de la vibración del mercado

Según esta teoría, el comportamiento humano no es aleatorio y crea vibraciones predecibles en todo el mercado. Gann operaba en los mercados financieros basándose en la idea de que el comportamiento humano colectivo forma un patrón repetitivo específico que se desarrolla a lo largo del tiempo.

Gann creía que los mercados se movían según leyes naturales, con relaciones matemáticas que regían cada movimiento de los precios. Su enfoque se basaba en tres pilares fundamentales:

1. Análisis de precios: relaciones matemáticas entre los niveles de precios.
2. Análisis temporal: patrones cíclicos y relaciones temporales geométricas.
3. Análisis de patrones: ángulos geométricos y proporciones naturales.

El cuadrado del precio y el tiempo

Más tarde formuló su teoría en lo que se conoce como el cuadrado del precio y el tiempo. Este concepto representa la piedra angular del enfoque matemático de Gann, según el cual los movimientos de los precios y los intervalos de tiempo siguen relaciones proporcionales basadas en progresiones de raíces cuadradas y ángulos geométricos.

Construcción y matemáticas de los gráficos oscilantes de Gann

Metodología básica de los gráficos oscilantes

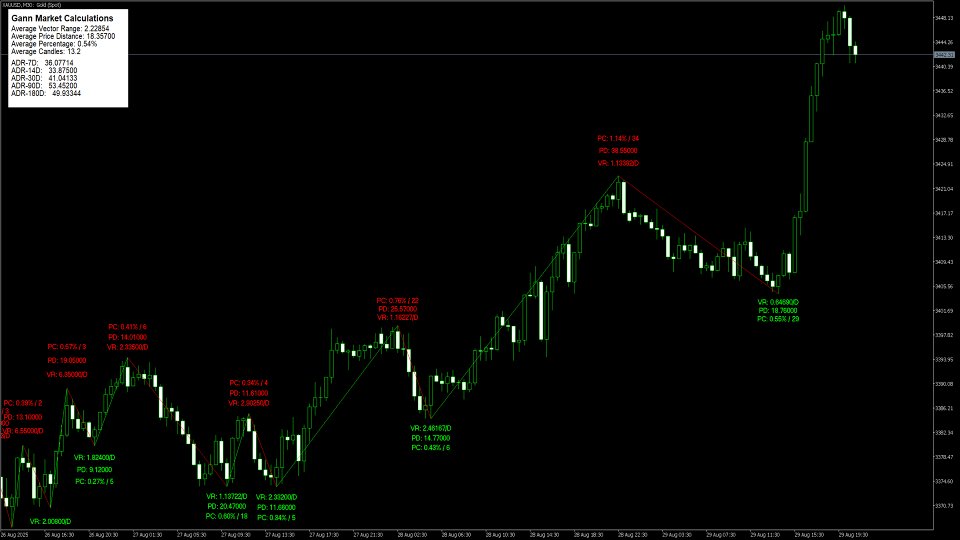
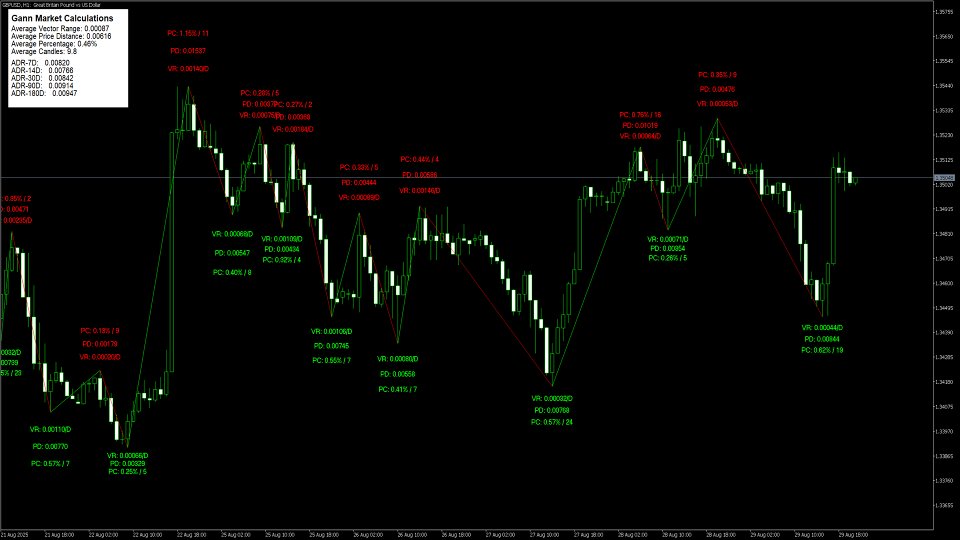
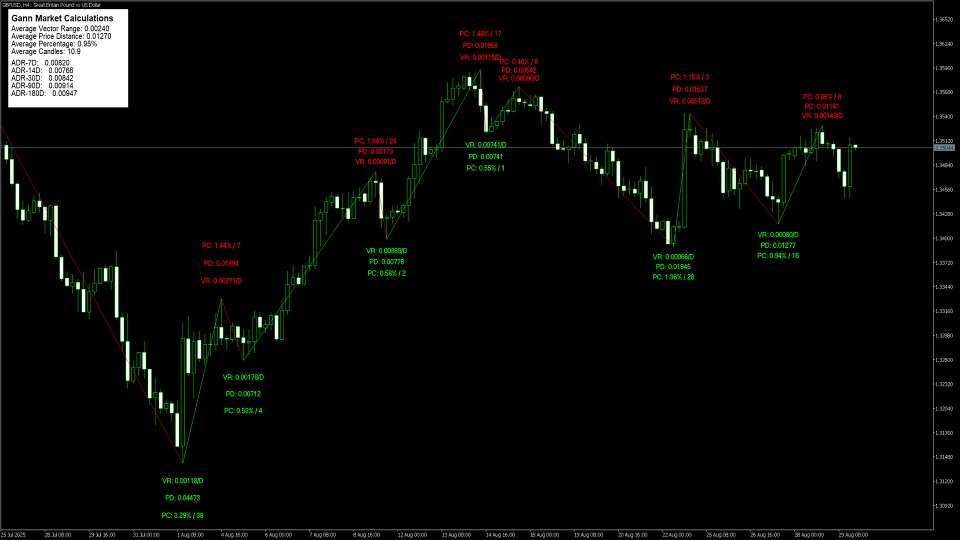
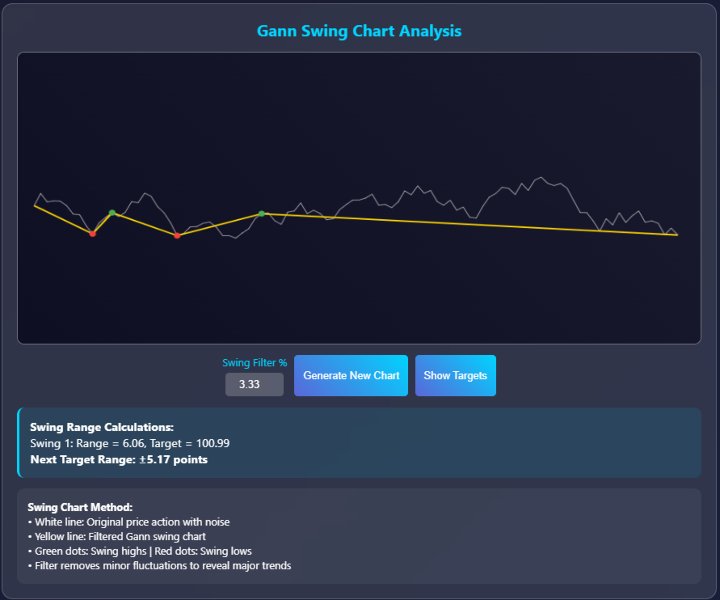
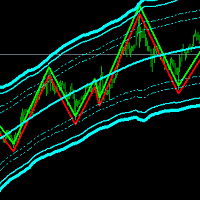
El método de los gráficos oscilantes de Gann filtra sistemáticamente la acción de los precios para identificar las oscilaciones significativas del mercado. El objetivo principal del uso de los gráficos de Gann es eliminar el "ruido" de los gráficos de precios regulares, revelando la estructura de tendencia subyacente.

Reglas matemáticas para la identificación de oscilaciones

Requisitos para la subida:

• El precio debe superar el máximo de la oscilación anterior en un porcentaje o valor en puntos predeterminado.
• El movimiento debe mantenerse por encima del nivel de ruptura durante un periodo de tiempo determinado.
• A menudo se requiere la confirmación del volumen para la validación

Requisitos de la fase descendente:

• El precio debe romper por debajo del mínimo de oscilación anterior según los mismos criterios matemáticos
• Ruptura sostenida por debajo del nivel de infracción
• Confirmación temporal de la nueva dirección de giro

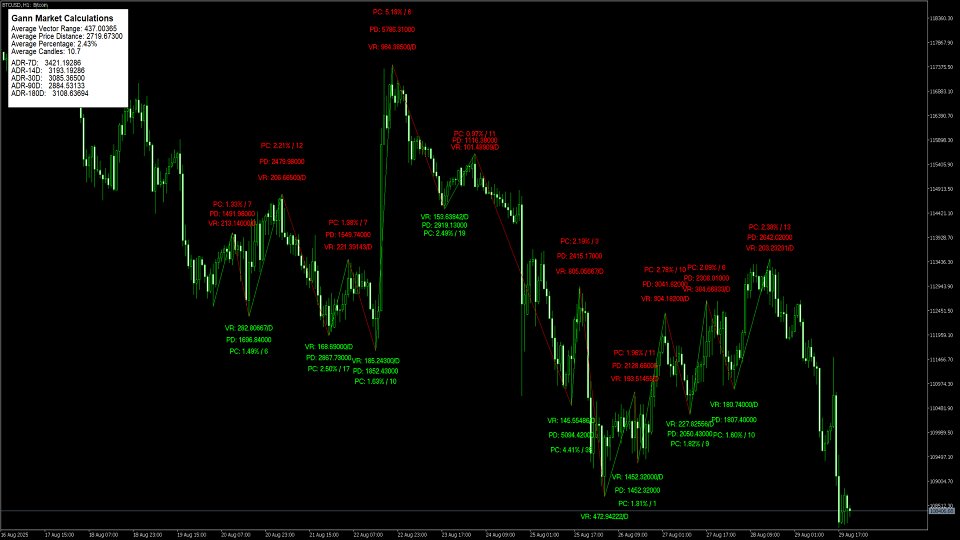
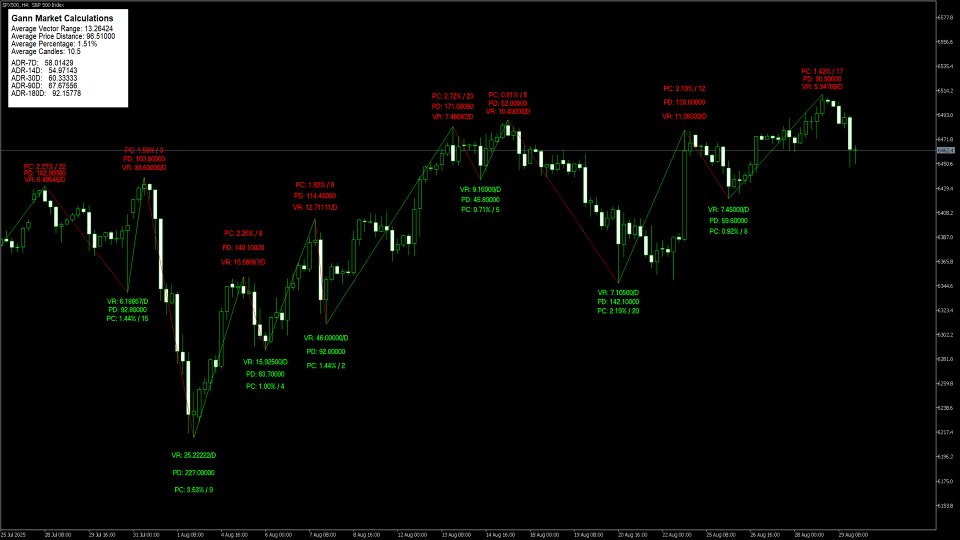
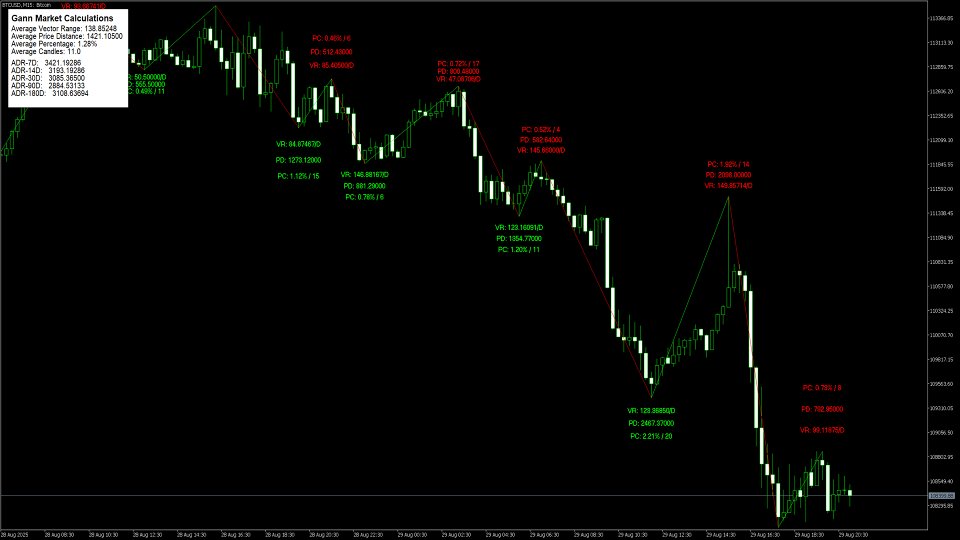
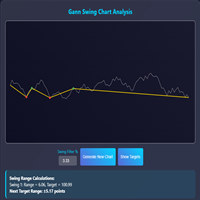
Fórmulas de cálculo del swing

Método de cálculo del rango

Objetivos Swing - añadir el rango a mover a la parte superior de ese movimiento para averiguar el objetivo para el próximo movimiento alcista o inverso en el mercado bajista.

Fórmula:

Objetivo del próximo swing = Extremo del swing actual + Rango del swing anterior

Donde:

• Extremo de oscilación actual = Máximo (tendencia alcista) o mínimo (tendencia bajista) del movimiento actual
• Rango de oscilación anterior = Diferencia absoluta entre el máximo y el mínimo de la oscilación anterior

Filtros de oscilación basados en porcentajes

Gann empleó filtros porcentuales específicos para definir las oscilaciones válidas:

Filtro de OscilaciónPequeña: 3-5% de movimiento del precioFiltro de Oscilación Media: 5-10% de movimiento del precio
Filtro de Oscilación Grande: 10%+ de movimiento del precio

Progresión de la raíz cuadrada en el análisis de swings

Gann descubrió que los niveles de precios significativos a menudo se alineaban con relaciones de raíz cuadrada:

Cálculo de la raíz cuadrada:

Próxima resistencia = √(Precio actual²) + 1 Próximo soporte = √(Precio actual²) - 1

El cuadrado de los números y el 50% de la diferencia entre esos cuadrados son soportes y resistencias significativos, pero no se pueden operar por sí mismos.

Conceptos matemáticos avanzados

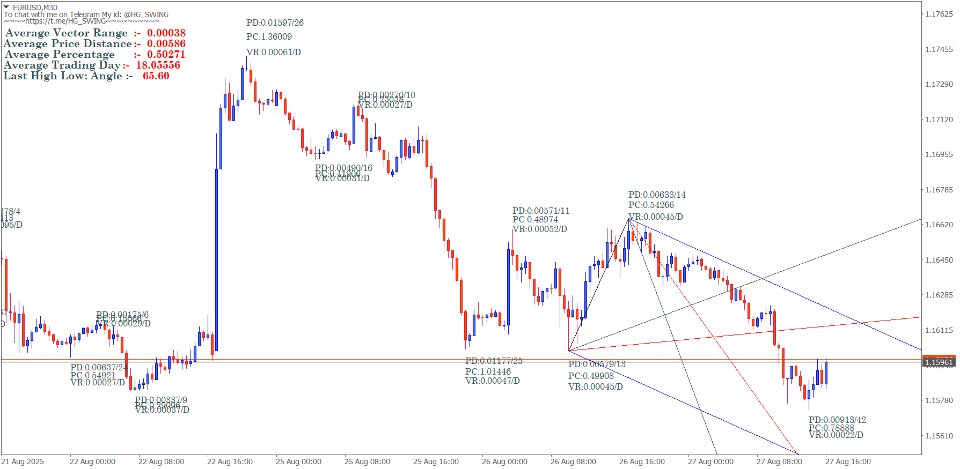
Ángulos de Gann y progresión geométrica

El sistema de ángulos de Gann representa una de sus aportaciones matemáticas más sofisticadas. Estos ángulos se derivan de la relación entre el precio y el tiempo utilizando proporciones geométricas específicas:

Ángulos de Gann primarios:

• 1×1 (ángulo de 45 grados) - Una unidad de precio por una unidad de tiempo
• 1×2, 1×3, 1×4, 1×8 - Relaciones precio-tiempo variables
• 2×1, 3×1, 4×1, 8×1 - Relaciones inversas

Construcción matemática de los ángulos de Gann

Cálculo del ángulo = arctan(Movimiento del precio / Movimiento del tiempo)

Para un ángulo 1×1 en un gráfico donde 1 día = $1:

• Pendiente = 1/1 = 1
• Ángulo = arctan(1) = 45 grados

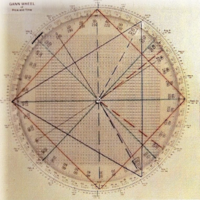
El cuadrado de nueve

Esto representa la herramienta matemática más compleja de Gann, incorporando:

Matemáticas en espiral: Números dispuestos en cuadrados en expansión con movimientos direccionales específicos que crean cálculos de resistencia y soporte.

Puntoscardinales: posiciones de 0° , 90°, 180°, 270° dentro del cuadradoPuntos cruzados: posiciones intermedias de 45° , 135°, 225°, 315

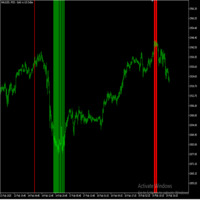
Cálculos del ciclo temporal

WD Gann, un famoso trader, creía que los movimientos del mercado estaban influenciados por ciclos temporales predecibles.

Periodos naturales:

• Ciclos solares (365 días)
• Ciclos lunares (29,53 días)
• Ciclos estacionales (trimestres de 90 días)
• Progresiones geométricas (7, 14, 21, 30, 45, 60, 90, 120, 180, 360 días)

Aplicación práctica de las matemáticas del Swing de Gann

Métodos de confirmación de tendencias

Para confirmar que una tendencia estaba en progreso, Gann buscaba la formación de máximos más bajos y mínimos más altos después de un cambio importante en la tendencia.

Confirmación de tendencia alcista:

1. El precio crea máximos oscilantes más altos
2. El precio mantiene los mínimos más altos
3. Los ángulos de Gann proporcionan soporte direccional

Confirmación de tendencia bajista:

1. El precio crea máximos oscilantes más bajos
2. El precio mantiene mínimos de oscilación más bajos
3. Los ángulos de Gann proporcionan resistencia direccional

Gestión del riesgo a través de las matemáticas

La principal filosofía de negociación de Gann consistía en operar con un stop loss cercano y seleccionar las operaciones más oportunas en la dirección de la tendencia principal.

Colocación matemática de Stop Loss:

• 3-5% por debajo de los mínimos para posiciones largas
• 3-5% por encima de los máximos para posiciones cortas
• Violaciones del ángulo de Gann como niveles alternativos de stop

Cálculos de objetivos de swing

Método de objetivo primario:

Objetivo = Precio de entrada ± (Rango de oscilación anterior × 1,0)

Método del objetivo secundario:

Objetivo = Precio de entrada ± (Rango de oscilación anterior × 1,618)

Método Objetivo Raíz Cuadrada:

Objetivo = Próximo nivel de raíz cuadrada perfecta

Aplicación moderna de las matemáticas de Gann

Adaptaciones a la era digital

Los operadores contemporáneos aplican los principios matemáticos de Gann utilizando:

Detección automatizada de oscilaciones: Algoritmos que identifican oscilaciones basándose en filtros porcentuales o basados en puntos.

Ángulos de Gann generados por ordenador: software que traza automáticamente líneas angulares basadas en relaciones matemáticas.

Herramientas de análisis de ciclos: Programas que identifican confluencias de ciclos temporales utilizando los periodos naturales de Gann

Combinación de matemáticas tradicionales con herramientas modernas

Integración de Fibonacci: Combinación de niveles de Gann con retrocesos de Fibonacci para el análisis de confluencias.

Análisis del perfil de volumen: uso de los niveles de precios de Gann con soportes y resistencias basados en el volumen

Análisis multitemporal: aplicación de los principios de oscilación de Gann en múltiples horizontes temporales

Análisis crítico y limitaciones

Precisión matemática frente a la realidad del mercado

Aunque el enfoque matemático de Gann proporciona un análisis estructurado del mercado, hay varias consideraciones que afectan a la aplicación práctica:

Subjetividad en la identificación de los puntos de giro: Diferentes operadores pueden identificar diferentes puntos de giro utilizando criterios idénticos.

Cambios en la estructura del mercado: Los mercados electrónicos modernos pueden no responder de forma idéntica a las relaciones matemáticas identificadas en la época de Gann.

Riesgo de ajuste de curvas: la complejidad de los métodos de Gann puede conducir a una optimización retrospectiva en lugar de a una precisión predictiva.

Equilibrio entre el rigor matemático y la psicología de la negociación

El éxito de la aplicación requiere comprender que la precisión matemática debe equilibrarse con:

• Análisis del sentimiento del mercado
• La consideración de los factores fundamentales
• Principios de gestión del riesgo
• Matemáticas de dimensionamiento de posiciones

Conclusión

El swing trading de W. D. Gann y las matemáticas de cálculo del mercado representan un sofisticado intento de descubrir la ley natural dentro de los mercados financieros. El legendario método de swing trading de W. D. Gann ha sido imparable durante los últimos 7 años. Su enfoque geométrico del análisis de los mercados, que combina la precisión matemática con los ciclos naturales, sigue influyendo en los operadores casi un siglo después de su desarrollo.

El atractivo perdurable de los métodos de Gann reside no sólo en su elegancia matemática, sino en su enfoque sistemático del análisis de los mercados, que elimina la toma de decisiones emocionales en las operaciones. Aunque los mercados modernos han evolucionado mucho desde la época de Gann, las relaciones matemáticas subyacentes que él identificó siguen proporcionando valiosos conocimientos a los operadores contemporáneos dispuestos a dominar su complejidad.

El éxito con los métodos de Gann requiere un estudio dedicado tanto de los fundamentos matemáticos como de las técnicas de aplicación práctica. La precisión geométrica de su enfoque exige una aplicación disciplinada, pero para quienes dominan estos cálculos, la metodología de swing trading de Gann ofrece una perspectiva única de la estructura del mercado que trasciende los enfoques convencionales del análisis técnico.

Nota: Las operaciones basadas en cualquier sistema matemático implican un riesgo significativo. El rendimiento histórico de los métodos analíticos no garantiza resultados futuros. Antes de poner en práctica cualquier estrategia de inversión basada en los principios matemáticos de Gann, es esencial una gestión adecuada del riesgo y la realización de pruebas retrospectivas exhaustivas.

link:- https://claude.ai/public/artifacts/4579f122-c256-455a-a251-a0c9f934cfd0