
Market math: profit, loss and costs
Contents
Introduction
While developing Expert Advisors, I have not paid any attention to what certain values mean when calculating profit or loss. Creation of EAs does not require delving into this issue. Indeed, why should I grasp all these values considering that MQL5 and even MQL4 contain all the necessary functionality to perform calculations? However, after a certain time and a certain amount of experience, questions inevitably start arising. Eventually, we begin to notice such details that previously seemed insignificant to us. After giving some thought to it, you realize that an EA is a pig in a poke. All data on the issue I managed to find on the Internet turned out to be scanty and unstructured. So I have decided to structure it myself. After reading this article, you will receive a complete and working mathematical model, as well as learn to understand and correctly calculate everything related to orders.
Equations for calculating profits or losses of orders
To develop an efficient trading system, first of all, it is necessary to understand how the profit or loss of each order is calculated. We are all able to calculate our profits and losses somehow to maintain our money management system. Someone does that intuitively, someone performs rough estimations, but almost any EA has the necessary calculations of all the necessary quantities.
Developing EAs disciplines your thoughts and makes you understand what and how is calculated, which is priceless. Now let's get to the point. It is worth starting with the simplest idea of how the profit of an order is calculated. Personally, I have always known that the profit calculation is quite complex in its essence, but is based on a few simple considerations. To simplify understanding, let's suppose that spread, swap and commission do not exist. I think, many people do not even take these values into account at first. Of course, the MQL5 language provides built-in functions, such as OrderCalcProfit, and possibly others, but in this article I want to go through the basics so that everyone understands what is calculated and how. Such meticulousness can be bewildering, but not paying attention to such parameters as spread, commission and swap is a fatal mistake that many traders make. Each of these values affects profit or loss in its own way. In my calculations, I will take everything into account and show how such little things can be of help. Profit and loss of orders excluding spreads, commissions and swaps:
- PrBuy = Lot * TickValue * [ ( PE - PS )/Point ] — profit for a buy order
- PrSell = Lot * TickValue * [ ( PS - PE )/Point ] — profit for a sell order
- Point — minimum possible price change on a selected symbol
- TickValue — profit value for a profitable position when the price moves by “1” Point
- PE — trade closing price (Bid)
- PS — trade opening price (Bid)
Such values as Point and TickValue in MQL5 are defined at the level of predefined variables or are available within the built-in functionality in the form of the return value of SymbolInfoDouble type functions. I will regularly touch the topic of MQL5 in my articles in one way or another because it is often possible to get to the bottom of many matters just by analyzing how MQL5 or its certain functionality is built.
Now let's slightly expand the understanding of this equation. A Buy order is opened at Ask, while a Sell order is opened at Bid. Accordingly, a Buy order is closed at Bid, while a Sell order is closed at Ask. Let's rewrite the equations taking into account the new amendments:
- PrBuy = Lot * TickValue * [ ( Bid2 – Ask1 )/Point ] — profit for a buy order
- PrSell = Lot * TickValue * [ ( Bid1 – Ask2 )/Point ] — profit for a sell order
- Bid1 — Sell trade open price
- Ask1 — Buy trade open price
- Bid2 — Buy trade close price
- Ask2 — Sell trade close price
The fragment of the specification below contains most of the data we will need later:

This is only part of the data that will be needed for the calculation. The rest of the data can be obtained using various built-in MQL5 functions. Let's take USDJPY as an example. In fact, we do not need a specification to write a code, but understanding where this data is displayed may prove very useful.
Let's go ahead and consider the commission this time. The commission per order can be calculated in various ways, but all the main methods come down to a percentage of lots we trade. There are other ways to charge a trading commission, but I will not consider them here since we will not need them. I will consider two possible scenarios for calculating the commission. I believe, they are sufficient. If we take the swap as a basis, then the swap examples may suggest another common calculation method that can be applied to the commission — calculation in points.
As a result, we have two seemingly different methods. However, as we will see, these methods are just a convenient form of perceiving the same “taxation” method, including the spread. Below are two equations for calculating the commission:
- Comission = Lot * TickValue * ComissionPoints
- Comission = Lot * ContractSize * BidAlpha * ComissionPercent/100
Here we see the new value “ContractSize”, which also has an implementation in MQL5 at the level of a built-in functionality that receives information from the trade server. This value is one of the most important ones and is present in absolutely all profit and loss calculations, although in an implicit form, in order to simplify the calculations for programmers. I see the validity of such simplifications from the programmer's point of view. But our current objective is to understand everything. You will see why this is needed towards the end of the article. Besides, I have introduced an additional BidAlpha variable. I will also reveal its meaning below. The following values specified in the symbol specification appear as well:
- ComissionPoints – commission in points
- ComissionPercent – commission as a percentage of the contract size
- BidAlpha = 1 (if the base currency is the same as the deposit currency)
- BidAlpha = Bid (of the selected symbol)
- BidAlpha = Bid (of the corresponding rate, where the base currency of the selected symbol is the same as the base currency of the transitional symbol, and the second currency is the same as the deposit currency)
- BidAlpha = 1/Ask (of the corresponding rate, where the base currency of the selected symbol is the same as the second currency of the transitional symbol, and the base currency is the same as the deposit currency)
Indeed, if the contract size is applied to the USDCHF pair, it is clear that the base currency of the selected pair is USD. Suppose we have a deposit in USD, then the transitional currency becomes USDUSD and, accordingly, its rate is always one. The second case is even simpler. Suppose that we have a EURUSD pair, which is also the conversion rate, so its Bid is the required value. The third case might be like this. Suppose that our currency is EURNZD. Then it turns out, we have to find the conversion rate from EUR and USD. The EURUSD rate and the Bid of this rate are what we need. In the fourth case, things are a little more complicated. Suppose that we have selected CHFJPY. It is clear that the transitional pair is USDCHF, since there is no CHFUSD exchange rate on Forex. Of course, we can create our own synthetic symbol and work with CHFUSD. In this case, we can use the previous case. But in fact, we just need to turn this symbol over, then its rate will become equal to “1/Ask” of the current "inconvenient" rate. In fact, we create a synthetic symbol without focusing on it. The same things are true for swaps. There are some other questions as well. For example, what rate should be used in the transitional currency - Bid, Ask or Mid? This question cannot be solved within the current approach. We will gradually come up with the right approach along the way. And now let's define the framework for improvement at least approximately. To do this, we should write at least the first approximate version of the general profit and loss equation, taking into account all the “taxation” options, such as spread, swap and commission.
To calculate swaps, we get similar equations:
- Swap = Lot * TickValue * SwapPoints * SwapCount(StartTime,EndTime)
- Swap = Lot * ContractSize * BidAlpha * SwapPercent/100 * SwapCount(StartTime,EndTime)
The equations are indeed pretty similar. The only difference is that the certain multiplier has appeared here in the form of the SwapCount function. I hope you will allow me some freedom of terminology. I call it the "function", because swaps are not charged immediately, while its size depends on the order opening and closing times. In a rough approximation, we can, of course, do without the multiplier and write the following:
- SimpleCount = MathFloor( (EndTime -StartTime) / ( 24 * 60 * 60 ) )
If we assume that EndTime and StartTime are of the 'datetime' type, then their difference is equal to the number of seconds between the order opening and closing points. The swap is charged once a day, so you just need to divide this value by the number of seconds in one day. This way we can get the first idea of how swap positions can be evaluated. Of course, this equation is far from perfect but it gives the answer to the question what kind of function it is and what it returns. Besides, it can suggest how (at least approximately) the swap is calculated. It returns the number of accrued swaps during the position lifetime. Similarly, the commission in the specification will be one of two possible values for the swap with the obligatory indication of the calculation method:
- SwapPoints – swap for a single position rollover in points
- SwapPercent – swap for a single position rollover in % of the contract size
If in the case of the commission the equations are simpler and do not require clarifications, then in case of the swap everything is much more complicated, but we will deal with the subtleties and nuances of these simplifications later. First, let's bring the profit and loss equations, excluding commissions and swaps, into a more consistent form:
- PrBuy = Lot * TickValue * [ ( Bid2 – (Bid1+S1*Point) )/Point ] — profit for a buy order
- PrSell = Lot * TickValue * [ ( Bid1 – (Bid2+S2*Point) )/Point ] — profit for a sell order
- S1 — spread when opening a buy order
- S2 — spread when closing a sell order
It is clear that Ask includes both spread and Bid. Let's separate the profit or loss of the order resulted from the spread, making it a separate summand:
- PrBuy = Lot * TickValue * [ ( Bid2 – Bid1)/Point ] + ( - Lot * TickValue * S1 ) — profit for a buy order
- PrSell = Lot * TickValue * [ ( Bid1 – Bid2)/Point ] + ( - Lot * TickValue * S2 ) — profit for a sell order
It can be seen that in both equations a certain summand has been separated, which is the part charged by the broker. Of course, this is not the whole amount, but at least now you can see more clearly what we get and what the broker takes. Note that in the first case, our “tax” on the spread depends only on the spread value when opening a “Buy” position, and in the second case, when closing a “Sell” position. It turns out that we give the broker part of our profit in the form of a spread exactly at the time of purchase at all times. Indeed, if we delve deeper into Forex trading, it becomes clear that opening a Buy position and closing a Sell position is an equivalent action confirmed by our equations. In this case:
- S1 — spread in points when opening any position
- S2 — spread in points when closing any position
These values are exactly the ones you can see in the Market Watch window if you want to display the spread. The corresponding built-in SymbolInfoInteger MQL5 function with the corresponding inputs returns exactly the same values. You can find the inputs in the MQL5 Help. My task in this case is to create a convenient mathematical calculation model tied to the MQL5 language so that these equations can be immediately coded into any EA or any other useful MQL5 code. Here is our summand, which is now similar to both swap and commission:
- SpreadBuy = - Lot * TickValue * S1
- SpreadSell = - Lot * TickValue * S2
Spread at opening and closing
Conventionally, the spread is calculated at the Buy point, but I will now show you why this is incorrect. I did a lot of market research, and the most predictable point of price movement turned out to be the “0:00” point. This is the transition point from one day to another. If you carefully observe this point, you will see approximately the same thing on all currency pairs — a jump towards the rate downward movement. This happens due to an increase in the spread at this point. The jump is followed by an equal rollback. What is spread? Spread is a gap between Bid and Ask. Conventionally, this gap is believed to be a consequence of the market depth. If the market depth is saturated with limit orders, the spread tends to zero, and if players leave the market, the spread increases. We can call this a market depth disintegration. Even at first sight, we can say that Bid is not the main thing here. It turns out that Ask and Bid are fundamentally equal. This is easy to understand if we imagine that, for example, it is possible to construct a USDEUR mirror instrument from “EURUSD”, and then Bid becomes Ask and, vice versa, Ask becomes Bid. Simply put, we just reverse the market depth.
The Ask line is usually not displayed on the chart, although that would be useful:
As we can see, Ask and Bid start to merge along with an increase in the chart period. Perhaps, due to these considerations, no terminal displays both lines, although I personally think that this is a necessary option. However, knowing about the presence of these values and their difference is not so important, because you can still use these things in an EA. I have not drawn Mid here, but I think everyone understands that this line is exactly in the middle between Bid and Ask. Clearly, for high periods the difference between these values practically does not play a role, and it seems like you do not even need to take into account the presence of Ask, but in fact it is necessary. These details are very important.
With this in mind, we can now say with absolute certainty that the middle of the market depth is an invariant during such transformations. This value can be calculated as follows:
- Mid = (Ask + Bid) / 2
Considering such a representation and using the last equation, we can see that:
- Bid = Mid * 2 – Ask
- Ask = Mid * 2 - Bid
Next:
- Bid = Mid * 2 – (Bid + S*Point) = Mid – (S*Point)/2
- Ask = Mid * 2 – (Ask - S*Point) = Mid + (S*Point)/2
These expressions can now be substituted into the original equations for calculating the profit or loss of orders. It was important to get exactly these expressions, because I want to show you something you did not understand before. It turns out that the amount charged by the broker actually depends not on the buy point solely, but on both entry and exit points, as well as on any position. Let's see what our equations will turn into when we insert new extended definitions there. We can see the following:
- PrBuy = Lot * TickValue * [ ( (Mid2 – (S2*Point)/2) – (Mid1 + (S1*Point)/2) ) )/Point ]
- PrSell = Lot * TickValue * [ ( (Mid1 – (S1*Point)/2) – (Mid2 + (S2*Point)/2) ) )/Point ]
After the appropriate transformations, we can see this:
- PrBuy = Lot * TickValue * [ (Mid2 – Mid1)/Point ] - Lot * TickValue * ( S1/2 + S2/2 )
- PrSell = Lot * TickValue * [ (Mid1 – Mid2)/Point ] - Lot * TickValue * ( S1/2 + S2/2 )
Considering that:
- Bid1 = Mid1 – (S1*Point)/2
- Bid2 = Mid2 – (S2*Point)/2
- Ask1 = Mid1 + (S1*Point)/2
- Ask2 = Mid2 + (S2*Point)/2
And keeping in mind that:
- Mid1 — middle of the market depth when opening any position
- Mid2 — middle of the market depth when closing any position
For convenience, we denote the negative summand defining the loss from spreads as follows:
- Spread = -Lot * TickValue * ( (S1*Point)/2 + (S2*Point)/2 )
And, accordingly, the summand indicating a profit or loss excluding spread, commission and swap, for example:
- ProfitIdealBuy = Lot * TickValue * [ (Mid2 – Mid1)/Point ]
- ProfitIdealSell = Lot * TickValue * [ (Mid1 – Mid2)/Point ]
Now we can write convenient equations considering all losses from spread, commission and swaps. Let's start with the expression prototype. Let's take the latest order profit and loss equations as a basis with the spread being the only thing considered here:
- TotalProfitBuy = ProfitIdealBuy + (Spread + Comission + Swap)
- TotalProfitSell= ProfitIdealSell + (Spread + Comission + Swap)
Perhaps, I should have written this equation at the very beginning, but I think that it is more appropriate here. We can see that the obscure TickValue is present almost everywhere. The main question is how it is calculated and how one and the same value can be used for calculation at different time points. Time points mean entries and exits from positions. I think, you understand that this value is dynamic in nature, and moreover, it is different for each trading symbol. Without decomposing this value into components, we will get errors that are larger the more distant "targets" we have. In other words, the obtained equations are only an approximation. There is an absolutely exact equation devoid of these shortcomings. The ratios obtained above serve as its limit. The limits themselves can be expressed as follows:
- Lim[ dP -> 0 ] ( PrBuy(Mid1, Mid1+dP… ) ) = TotalProfitBuy(Mid1, Mid1+dP…)
- Lim[ dP -> 0 ] ( PrSell(Mid1, Mid1+dP… ) ) = TotalProfitSEll(Mid1, Mid1+dP…)
- Mid1+dP = Mid2 — the new price is obtained from the previous one plus the delta tending to zero
- TotalProfitBuy = TotalProfitBuy(P1,P2… ) — as it was determined, profit or loss is a function of Mid values and many others
- TotalProfitSell = TotalProfitSell(P1,P2… ) — similar
In general, equivalent limits for a general understanding of the situation can be drawn up in many ways. There is no need to multiply them. In our case, one is sufficient for clarity.
Although we have received some equations and they even work, the limits of applicability are very conditional. Next, we will be engaged in obtaining the initial equations entailing such approximate equations. Without knowing the building blocks a profit or a loss is built from, we will never get these equations. In turn, these equations will help us not only find the most accurate ratios for calculating profit and loss, but also find the imbalance of market processes, which can subsequently yield a profit.
Most accurate method for calculating the profit and loss of orders
In order to understand how to build these equations, we need to get back to the basics, namely what are Buy and Sell. But first, I think it is important to remember that buying actually means exchanging your money for a product. Another currency can be viewed as a commodity since it symbolizes the ability to own certain goods. Then it is clear that the sale is the reverse process of exchanging the second currency for the first. But if we omit all the conventions, it turns out that buying and selling are equivalent actions. One currency is exchanged for another and the only difference is which currency we give away and which one we receive in return.
While searching for information about these calculations, I found strange conventions I personally was unable to grasp for quite a long time, because they have no basis. Since I am a techie having quite a lot of experience in studying various technical material, I have determined two very simple truths. If the material is not clear for you and raises questions, then:
- The authors do not fully understand it themselves, so they do their best to convince you of the opposite by all means (this is usually done using anti-logical statements)
- Details are deliberately omitted in order to hide unnecessary information from you.
The image below develops the idea further making it easier to understand. It shows opening and closing two types of market orders:
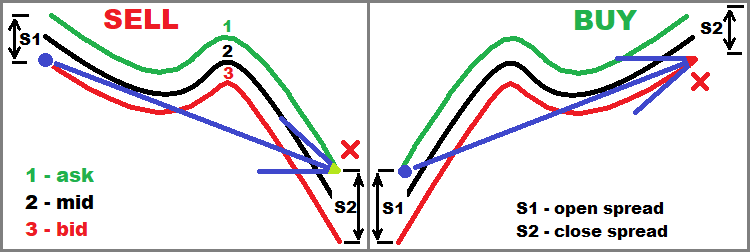
Now, I think the spreads section and the current section will become clearer. In general, this image is relevant for the entire article, but it is most useful in this block.
Of course, I am sure that there are correct calculations in the specialized literature, but it is obvious that finding this information is more difficult than guessing what is missing on your own. The convention states that when we buy, for example, EURUSD, we buy EUR and sell USD. Let's write this out:
- EUR = Lot * ContractSize
- USD = - Ask1 * Lot * ContractSize = - (Bid1 + S1*Point) * Lot * ContractSize
In this case, it turns out that when buying, we get a positive amount of the base currency and a negative amount of the second currency. I believe, I am not the only one who thinks this is complete nonsense. After giving some though to it, I came to the conclusion that the ratios are correct, but they are presented in a rather unintuitive way. Let's change it the following way… To buy EUR, we need another currency USD, which we should take from our balance sheet, borrow from a broker or use both methods. In other words, we first take USD from some shared storage borrowing it. It looks like this:
- USD1 = Ask1 * Lot * ContractSize = (Bid1 + S1*Point) * Lot * ContractSize — this is what we borrowed
- EUR1 = Lot * ContractSize — this is what we bought with borrowed funds at the Ask exchange rate at the time of purchase
The negative value will appear later. In fact, it cannot be here at the moment. The negative value appears when we close our position. So, if the position is open, then it should be closed. It turns out that we need to perform the Sell action using the same lot. If we adhere to standard considerations:
- EUR2 = Lot * ContractSize
- USD2 = Bid2 * Lot * ContractSize
It turns out that we already sell EUR and buy USD. Regard our transformations, it turns out that we take those EUR we exchanged borrowed funds for from ourselves and change them back to the borrowed currency. A profit or a loss will be obtained by subtracting borrowed funds from the received funds:
- Profit_EUR = EUR1 – EUR2 = 0
- Profit_USD = USD2 – USD1 = Bid2 * Lot * ContractSize - (Bid1 + S1*Point) * Lot * ContractSize = Lot * ContractSize * ( Bid2 – Bid1 – S1*Point)
It turns out that the EUR disappears and only USD remain. If our deposit is made in USD, then we do not need to convert the resulting currency into the deposit currency, since they are the same. The equation is very similar to the one that we took as a basis at the very beginning, the only difference is that commission and swap are not taken into account here because they are considered separately. Let's now rewrite this expression a bit:
- Profit_USD = Lot * (ContractSize*Point) * [ ( Bid2 – Bid1 – S1*Point) / Point ]
Here we simply divide and multiply the right side by Point and get our original equation. The same equation can be obtained if we use the original system of conventions stating that we sell and buy at the same time regardless of a trade direction. In this case, everything borrowed has a minus sign, symbolizing that we owe, while the purchased amount is left with a plus sign. In such a system of conventions, we do not need to consider what we are changing to what and from where. Let's do the same using this approach:
- EUR1 = Lot * ContractSize
- USD1 = - Ask1 * Lot * ContractSize = - (Bid1 + S1*Point) * Lot * ContractSize
This is a buy. Action one.
- EUR2 = - Lot * ContractSize
- USD2 = Bid1 * Lot * ContractSize
This is a sell. Action two.
Further on, everything is simplified, because we do not need to think about what to subtract from what and how. We simply need to add up all EUR and all USD separately. The base currency disappears anyway leaving only the second currency. Let's add up and make sure that the equations are identical to the previous ones:
- Profit_EUR = EUR1 + EUR2 = 0
- Profit_USD = USD1 + USD2 = - (Bid1 + S1*Point) * Lot * ContractSize + Bid2 * Lot * ContractSize = Lot * ContractSize * ( Bid2 – Bid1 – S1*Point)
It turns out that the profit of any symbol is considered exclusively in the second currency (not the base one), and the base currency always disappears during the full open-close cycle. Naturally, everything is mirrored for selling. Let's write all this to make our calculations complete. Now we sell EURUSD, and then we close this position by doing a "Buy":
- EUR1 = - Lot * ContractSize
- USD1 = Bid1 * Lot * ContractSize
This is a sell. Action one.
- EUR2 = Lot * ContractSize
- USD2 = - (Bid2 + S2*Point) * Lot * ContractSize
This is a buy, action two.
Now let's add all the values in the same way:
- Profit_EUR = EUR1 + EUR2 = 0
- Profit_USD = USD1 + USD2 = Bid1 * Lot * ContractSize - (Bid2 + S2*Point) * Lot * ContractSize = Lot * ContractSize * ( Bid1 – Bid2 – S2*Point)
As you can see, the equation differs only in that Bid1 and Bid2 are swapped. And of course, the spread is charged at the closing point of the position, because the closing point is the buy point. So far, everything is in strict accordance with the original equations. It is also worth noting that now we know what TickValue is, at least if the second currency (not the base one) of our symbol matches the currency of our deposit. Let's write the equation of this value:
- TickValue = ContractSize * Point
However, this value is again suitable only for symbols, in which the currency of a profit equals the currency of our deposit. But what if we use, say, a cross rate, such as AUDNZD? The main thing here is not the symbol itself, but the fact that this value is always calculated in relation to the currency of our deposit, and we receive it from the trade server. But if we use this equation in relation to the cross rate, then it turns out that it, of course, works, but it will respond to us not in our deposit currency, but in the symbol's second currency. To convert this into the deposit currency, it is necessary to multiply this value by a certain ratio, which, in fact, is the conversion rate we considered in the previous block.
- TickValueCross = ContractSize * Point * BidAlphaCross
The conversion rate calculation is pretty simple:
- Look at the second currency in our symbol (not the base one)
- Look for a symbol that contains this currency and the currency of our deposit
- Make an exchange at the appropriate rate
- If necessary, transform the symbol (mirror course)
For example, if we trade EURCHF, and we have a deposit in USD, then the initial profit will be in CHF, so we can use the USDCHF instrument and its rate. So, we need to exchange CHF for USD, then it turns out that we need to buy USD for CHF. But since CHF = PBid * USD, then USD = (1/PAsk) * CHF and accordingly:
- BidAlphaCross = 1/PAsk
Let's use another symbol for the second example. For example, we trade AUDNZD, and we get profit in NZD, then we can take the NZDUSD rate and, since USD = PBid * NZD, then in this case:
- BidAlphaCross = PBid
Let's figure it out. Converting CHF to USD means “+USD ; -CHF”. In other words, we lose one currency and gain another. This means buying USD, selling at the USDCHF rate, at the price of PAsk, which actually means just the following: “USD = (1/PAsk) * CHF”. It is easier to perceive it in the following way: when buying, we should receive a little less USD than it could be if the broker took nothing from our exchange operation. This means that if we divide by a larger PAsk, we get a value smaller than 1/P.
In the second case, the situation is reversed. Converting NZD to USD means “+USD ; -NZD”, which means selling at the PBid price using the NZDUSD rate. Let's set a similar ratio for “USD = PBid * NZD”. The exchange is again made at a slightly worse rate, which is “PBid”. Everything matches. All is transparent and easy to grasp. Keep in mind that the primary perfect rate is "PMid", which I considered above. Considering this, it is easy to understand that the spread is nothing but the percentage the broker charges in the form of the exchanged currency. Therefore, each trade, whether it is opening or closing a position, is accompanied by a broker's tax on currency exchange called the spread. The rest of this tax is contained in commission and swap.
The conversion rate is not required and the ratio is equal to one only if the profit currency matches the currency of our deposit, so the ratio disappears in case of major currency pairs and makes the tick size fixed for all these pairs. As in the previous case, our trading symbol may turn out to be a transitional rate, so we do not have to search for it among other symbols.
Considering the presence of the new BidAlphaCross value, rewrite the order profit and loss equations without commission and swap:
- BuyProfit = BidAlphaCross * Lot * ContractSize * ( Bid2 – Bid1 – S1*Point)
- SellProfit = BidAlphaCross * Lot * ContractSize * ( Bid1 – Bid2 – S2*Point)
Taking into account that:
- Bid1 = Mid1 – (S1*Point)/2
- Bid2 = Mid2 – (S2*Point)/2
Let's rewrite the equations in a more visual form, substituting the ratios for Mid there:
- BuyProfit = BidAlphaCross * Lot * ContractSize * ( Mid2 – (S2*Point)/2 – Mid1 + (S1*Point)/2 – S1*Point)
- SellProfit = BidAlphaCross * Lot * ContractSize * ( Mid1 – (S1*Point)/2 – Mid2 + (S2*Point)/2 – S2*Point)
Let's simplify all this:
- BuyProfit = Lot * BidAlphaCross * ContractSize * Point * [ ( Mid2 – Mid1 )/ Point - ( S1/2 + S2/2 ) ]
- SellProfit = Lot * BidAlphaCross * ContractSize * Point * [ ( Mid1 – Mid2 )/ Point - ( S1/2 + S2/2 ) ]
Yet more simplification:
- BuyProfit = Lot * TickValueCross * [ ( Mid2 – Mid1 )/ Point ] - Lot * TickValueCross * ( S1/2 + S2/2 )
- SellProfit = Lot * TickValueCross * [ ( Mid1 – Mid2 )/ Point ] - Lot * TickValueCross * ( S1/2 + S2/2 )
Now, I think, it has become easier and clearer. I deliberately removed the summand associated with the spread, so that we can see that this is exactly the charged value, regardless of how long our position or order remains active.
Swap exact calculation function
Now it remains to clarify the swap equations. Let's recall the equations that we received at the beginning of the article:
- Swap = Lot * TickValue * SwapPoints * SwapCount(StartTime,EndTime)
- Swap = Lot * ContractSize * BidAlpha * SwapPercent/100 * SwapCount(StartTime,EndTime)
In the last block, we found out that TickValue is not a single-digit value and is calculated differently for different currency pairs. It was determined that:
- TickValue = ContractSize * Point
But this only works for those pairs where the profit currency matches the deposit currency. In more complex cases, we use the following value:
- TickValueCross = ContractSize * Point * BidAlphaCross
where BidAlphaCross is also a different value, which depends on the deposit currency and the selected symbol. All this we have defined above. Based on this, we need to rewrite the first version of the equation replacing the standard constant:
- Swap = Lot * TickValueCross * SwapPoints * SwapCount(StartTime,EndTime)
But this equation is still far from perfect. This is because, unlike a commission or a spread, a swap can be credited an arbitrarily large number of times while your position remains open. It turns out that in the case of cross rates, one TickValueCross value is not enough to describe the entire total swap, because it turns out that at each swap accrual point, this value is slightly different because the BidAlphaCross value changes. Let's write the complete equations for calculating swaps for the two "taxation" options:
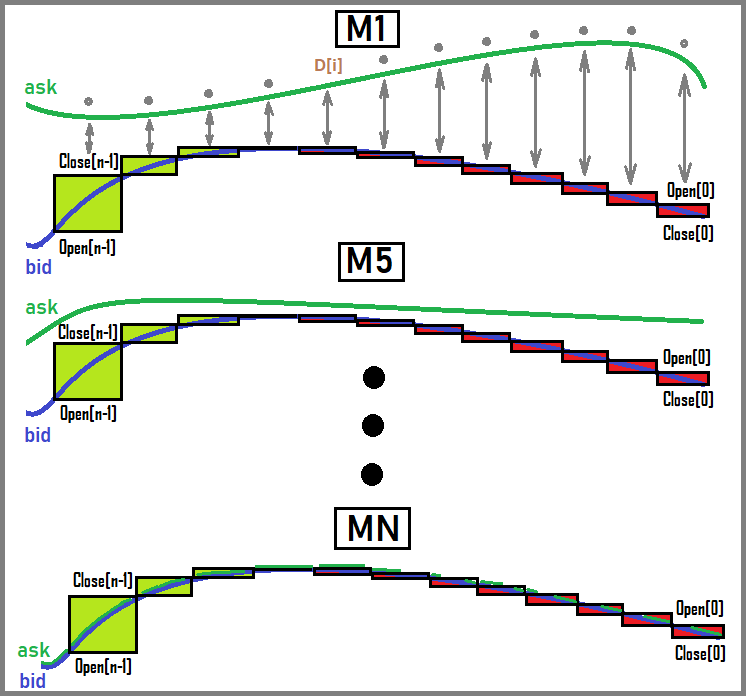
- Swap = SUMM(1 … D) { Lot * (SwapPoints * K[i]) * TickValueCross[i] } — sum of all accrued swaps in points, for each crossed point 0:00
- Swap = SUMM(1 … D) { Lot * ContractSize * BidAlpha[i] * (SwapPercent/100 * K[i]) * } — in %
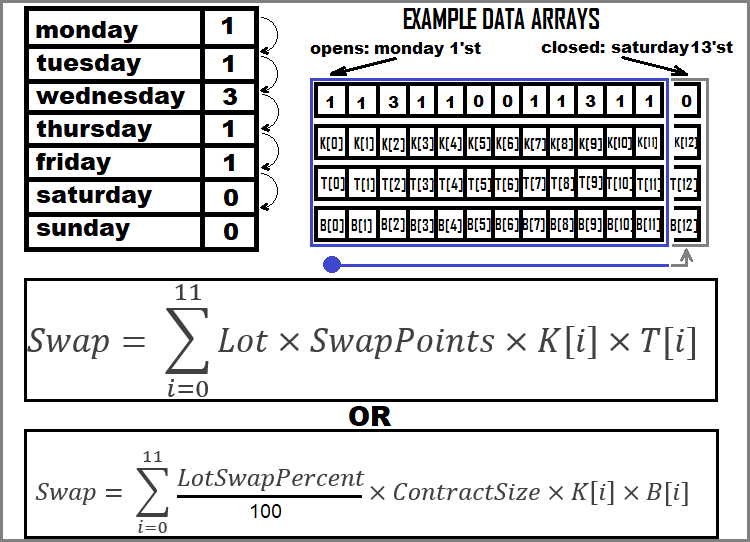
Arrays to sum:
- K[i] = 1 or 3 — if the ratio is “3”, this means that it was the day of the triple swap accrual
- TickValueCross[i] — array of tick sizes at swap points
- BidAlpha[i] — array of adjustment rates at points of swap charging
Let's look at an example of swap calculation for an arbitrary order. To do this, I will introduce the following short notations:
- TickValueCross[i] = T[i]
- BidAlpha[i] = B[i]
- K[i] = K[i]
Now let's graphically depict how we will sum the swaps:
We have analyzed all possible examples of calculating the order profit and loss.
Practical part
In this section, we will test our mathematical model. In particular, I would pay special attention to the issues of calculating profit or loss without taking into account commissions and swaps. If you remember, I was wondering at what time point I should calculate the TickValueCross value if we calculate the profit at the cross rate? This moment is the only uncertainty in the entire model I am going to test. To do this, let's first implement all the necessary functionality to calculate the profit or loss of any order using our mathematical model, test it in the strategy tester, and after all this, compare our calculations with real order data from the trading history. The final goal is to test our mathematical model and compare it with the MQL5 reference function such as OrderCalcProfit at the same time.
In order to evaluate all this, it is necessary to introduce four quantities:
- Real — order profit from history
- BasicCalculated — the same profit calculated when opening an order using the OrderCalcProfit function
- CalculatedStart — profit calculated at the time of opening the order using our mathematical model
- CalculatedEnd — profit calculated at the time of closing the order using our mathematical model
This entails three types of average deviation of the profit value:
- AverageDeviationCalculatedMQL = Summ(0..n-1) [ 100 * MathAbs(BasicCalculated - Real)/MathAbs(Real) ] / n : relative profit deviation by MQL5 code
- AverageDeviationCalculatedStart = Summ(0.. n-1 ) [ 100 * MathAbs(CalculatedStart - Real)/MathAbs(Real) ] / n : relative profit deviation by our code when opening an order
- AverageDeviationCalculatedEnd = Summ(0.. n-1 ) [ 100 * MathAbs(CalculatedEnd - Real)/MathAbs(Real) ] / n : relative profit deviation by our code when closing an order
Similarly to this, you can enter three types of maximum deviation:
- MaxDeviationCalculatedMQL = Max(0.. n-1 ) [ (100 * MathAbs(BasicCalculated - Real)/MathAbs(Real)) ] - relative profit deviation by MQL5 code
- MaxDeviationCalculatedStart = Max(0.. n-1 ) [ (100 * MathAbs(CalculatedStart - Real)/MathAbs(Real)) ] - relative profit deviation by our code when opening an order
- MaxDeviationCalculatedEnd = Max(0.. n-1 ) [ (100 * MathAbs(CalculatedEnd - Real)/MathAbs(Real)) ] - relative profit deviation by our code when closing an order
where:
- Summ(0..n-1) — sum of all relative deviations of all "n" orders
- Max(0..n-1) — maximum relative deviation from all "n" orders
We can test our mathematical model by implementing these calculations in the code of an arbitrary EA. Let's start by implementing our profit equation. I have made this the following way:
double CalculateProfitTheoretical(string symbol, double lot,double OpenPrice,double ClosePrice,bool bDirection) { //PrBuy = Lot * TickValueCross * [ ( Bid2 - Ask1 )/Point ] //PrSell = Lot * TickValueCross * [ ( Bid1 - Ask2 )/Point ] if ( bDirection ) { return lot * TickValueCross(symbol) * ( (ClosePrice-OpenPrice)/SymbolInfoDouble(symbol,SYMBOL_POINT) ); } else { return lot * TickValueCross(symbol) * ( (OpenPrice-ClosePrice)/SymbolInfoDouble(symbol,SYMBOL_POINT) ); } }
Here we have two equations in one: for buying and for selling. The "bDirection" marker is responsible for this. The additional function calculating the tick size is highlighted in green. I have implemented it the following way:
double TickValueCross(string symbol,int prefixcount=0) { if ( SymbolValue(symbol) == SymbolBasic() ) { return TickValue(symbol); } else { MqlTick last_tick; int total=SymbolsTotal(false);//symbols in Market Watch for(int i=0;i<total;i++) Symbols[i]=SymbolName(i,false); string crossinstrument=FindCrossInstrument(symbol); if ( crossinstrument != "" ) { SymbolInfoTick(crossinstrument,last_tick); string firstVAL=StringSubstr(crossinstrument,prefixcount,3); string secondVAL=StringSubstr(crossinstrument,prefixcount+3,3); if ( secondVAL==SymbolBasic() && firstVAL == SymbolValue(symbol) ) { return TickValue(symbol) * last_tick.bid; } if ( firstVAL==SymbolBasic() && secondVAL == SymbolValue(symbol) ) { return TickValue(symbol) * 1.0/last_tick.ask; } } else return TickValue(symbol); } return 0.0; }
There are also two implementations inside for the following cases:
- Profit currency of the symbol is the same as the currency of our deposit
- All other cases (looking for a transitional rate)
The second scenario also divides into two cases:
- The deposit currency is at the top of the conversion rate
- The deposit currency is at the bottom of the conversion rate
Everything is in strict accordance with the mathematical model. In order to implement the last divisions, we first need to find the right tool to calculate the conversion rate:
string FindCrossInstrument(string symbol,int prefixcount=0) { string firstVAL; string secondVAL; for(int i=0;i<ArraySize(Symbols);i++) { firstVAL=StringSubstr(Symbols[i],prefixcount,3); secondVAL=StringSubstr(Symbols[i],prefixcount+3,3); if ( secondVAL==SymbolBasic() && firstVAL == SymbolValue(symbol) ) { return Symbols[i]; } if ( firstVAL==SymbolBasic() && secondVAL == SymbolValue(symbol) ) { return Symbols[i]; } } return ""; }
To do this we need to know how to "take out" the base currency from a symbol name:
string SymbolValue(string symbol,int prefixcount=0) { return StringSubstr(symbol,prefixcount+3,3); }
And get the profit currency using the built-in MQL5 function:
string SymbolBasic() { return AccountInfoString(ACCOUNT_CURRENCY); }
Compare all this with currencies in all Market Watch symbols before the first match. Now we can use this functionality at the time of opening and closing orders. If you wish, you can see the rest of the code in the file attached below. I added the calculation of deviations after the end of the backtest. They are written to the terminal log. I tested all twenty-eight major currency pairs and cross rates, and put the result in a table so that we can evaluate the performance of our mathematical model and compare it with the MQL5 implementation. The results were divided into three conditional blocks. The first two look as follows:
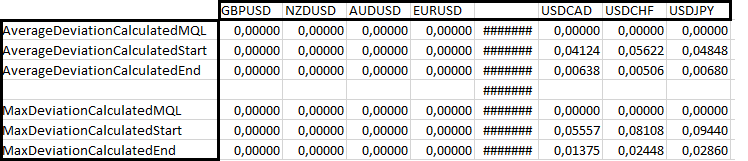
As you can see, for the first four currency pairs, both the MQL5 and our implementation work perfectly because the profit currency is the same as the deposit one. Next comes a block of three currency pairs, in which the base currency is the same as the profit currency. In this case, the MQL5 implementation works best, but nevertheless, it is already clear that the calculation error when opening an order is much higher than the same error when closing. This indirectly shows that the calculation should really be performed at the moment the order is closed. Let's have a look at other currency pairs:
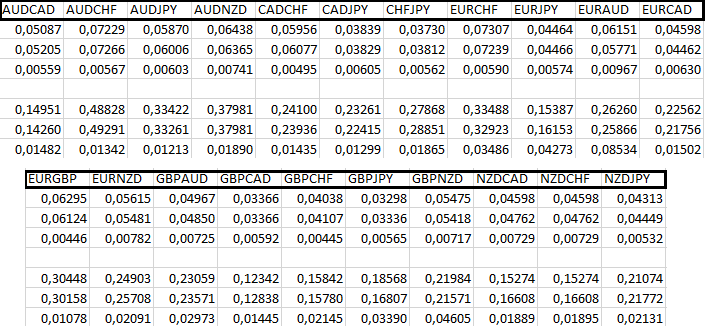
Here my functionality is not inferior to the basic MQL5 one. In addition, it is clear that the calculations performed when closing a position are much more accurate at all times. The only thing I cannot explain is the presence of zeros in the first line of the second block. There can be many reasons, but it seems to me that they are not related to my model, although I can be wrong. As for checking equations for commissions and swaps, I do not think it is necessary. I am confident in those equations as there is nothing particularly tricky about them.
Conclusion
In this article, I have come up with a mathematical model created from scratch and guided only by fragments of information. The model contains everything you need to calculate orders for major currency pairs and cross rates. The model has been tested in the strategy tester and is ready for immediate use in any EA, indicator or useful script. In fact, the applicability of this model is much wider than just calculating profits, losses or costs, but this is a topic for another article. You can find all the necessary functionality and examples of its use in the research EA that I used to compile the table. The EA is attached to the article. You can run it yourself and compare the results with the table. Most importantly, I believe that I have managed to create a simple and logical "manual".
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/10211
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 DIY technical indicator
DIY technical indicator
 Developing a trading Expert Advisor from scratch (Part 27): Towards the future (II)
Developing a trading Expert Advisor from scratch (Part 27): Towards the future (II)
 Learn how to design a trading system by Fractals
Learn how to design a trading system by Fractals
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
... but if it's important to correct of course ...
-- here TickSize is correct -- well, and further on in the text.
-- here TickSize is correct -- well, and further on in the text
I have everything correct, otherwise the calculations would not add up. I made a short script. It is not for you personally, but for everyone. These values are different and you should understand their difference. I'll think how to correct it. But in this case, everything is correct. There is no need to cross out.
I would like to point out that there is a major flaw regarding the calculations of profit/loss in this article.
You are using Tick Value and Point Size together. That is incorrect. You should be using Tick Value with Tick Size, not Point Size.
Also the Point Size is not the smallest change in price. That would be the Tick Size. Point Size is the smallest numerical resolution required to represente the price quote, not the smallest price change.
Here are examples of symbols with different point and tick sizes ...
There is another flaw with your approach: you use the sell rate of the conversion pair (Bid or 1/Ask if indirect) for all trade types, whether buy or sell.
This is not correct. The rate used for conversion of profits/losses from profit currency -> account currency, must match the trade type on the traded pair.
It is a simple rule: The trade type on the conversion pair is the same as that of the traded pair.
The choice of price type (BID/ASK) of the profit/account conversion pair depends to two things: (a) the type of the order (b) position of account currency in the conversion pair (first or second).