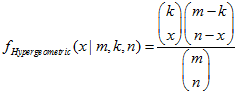#include <Graphics\Graphic.mqh>
#include <Math\Stat\Hypergeometric.mqh>
#include <Math\Stat\Math.mqh>
#property script_show_inputs
//--- input parameters
input double m_par=60; // Gesamtzahl der Objekte
input double k_par=30; // Anzahl der Objekte mit der gewünschten Eigenschaft
input double n_par=30; // Anzahl der gezogenen Objekte
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//--- Anzeige des Preischarts deaktivieren
ChartSetInteger(0,CHART_SHOW,false);
//---
MathSrand(GetTickCount());
//--- Stichprobe einer zufälligen Größe erzeugen
long chart=0;
string name="GraphicNormal";
int n=1000000; // Anzahl der Werte in der Stichprobe
int ncells=15; // Anzahl der Intervalle im Histogramm
double x[]; // Zentren der Intervalle des Histogramms
double y[]; // Anzahl der Werte aus der Stichprobe, die innerhalb des Intervalls liegen
double data[]; // Stichprobe
double max,min; // der höchste und der niedrigste Werte in der Stichprobe
//--- Stichprobe aus der hypergeometrischen Verteilung erhalten
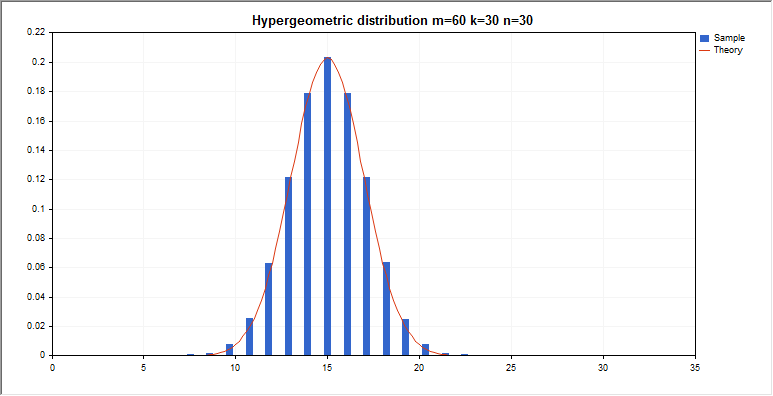
MathRandomHypergeometric(m_par,k_par,n_par,n,data);
//--- Daten für das Zeichnen des Histogramms berechnen
CalculateHistogramArray(data,x,y,max,min,ncells);
//--- Grenzen der Sequenz und Schritt für das Zeichnen einer theoretischen Kurve erhalten
double step;
GetMaxMinStepValues(max,min,step);
PrintFormat("max=%G min=%G",max,min);
//--- theoretisch berechnete Daten im Intervall [min,max] erhalten
double x2[];
double y2[];
MathSequence(0,n_par,1,x2);
MathProbabilityDensityHypergeometric(x2,m_par,k_par,n_par,false,y2);
//--- skalieren
double theor_max=y2[ArrayMaximum(y2)];
double sample_max=y[ArrayMaximum(y)];
double k=sample_max/theor_max;
for(int i=0; i<ncells; i++)
y[i]/=k;
//--- Charts ausgeben
CGraphic graphic;
if(ObjectFind(chart,name)<0)
graphic.Create(chart,name,0,0,0,780,380);
else
graphic.Attach(chart,name);
graphic.BackgroundMain(StringFormat("Hypergeometric distribution m=%G k=%G n=%G",m_par,k_par,n_par));
graphic.BackgroundMainSize(16);
//--- plot all curves
graphic.CurveAdd(x,y,CURVE_HISTOGRAM,"Sample").HistogramWidth(6);
//--- und nun die theoretische Kurve der Verteilungsdichte zeichnen
graphic.CurveAdd(x2,y2,CURVE_LINES,"Theory").LinesSmooth(true);
graphic.CurvePlotAll();
//--- plot all curves
graphic.Update();
}
//+------------------------------------------------------------------+
//| Calculate frequencies for data set |
//+------------------------------------------------------------------+
bool CalculateHistogramArray(const double &data[],double &intervals[],double &frequency[],
double &maxv,double &minv,const int cells=10)
{
if(cells<=1) return (false);
int size=ArraySize(data);
if(size<cells*10) return (false);
minv=data[ArrayMinimum(data)];
maxv=data[ArrayMaximum(data)];
double range=maxv-minv;
double width=range/cells;
if(width==0) return false;
ArrayResize(intervals,cells);
ArrayResize(frequency,cells);
//--- Zentren der Intervalle setzen
for(int i=0; i<cells; i++)
{
intervals[i]=minv+(i+0.5)*width;
frequency[i]=0;
}
//--- Frequenzen des Auftretens innerhalb des Intervalls füllen
for(int i=0; i<size; i++)
{
int ind=int((data[i]-minv)/width);
if(ind>=cells) ind=cells-1;
frequency[ind]++;
}
return (true);
}
//+------------------------------------------------------------------+
//| Calculates values for sequence generation |
//+------------------------------------------------------------------+
void GetMaxMinStepValues(double &maxv,double &minv,double &stepv)
{
//--- die absolute Spannweite der Sequenz berechnen, um die Genauigkeit der Normalisierung zu erhalten
double range=MathAbs(maxv-minv);
int degree=(int)MathRound(MathLog10(range));
//--- den höchsten und den niedrigsten Wert mit der angegebenen Genauigkeit normalisieren
maxv=NormalizeDouble(maxv,degree);
minv=NormalizeDouble(minv,degree);
//--- den Schritt der Erzeugung einer Sequenz auch basierend auf der angegebenen Genauigkeit setzen
stepv=NormalizeDouble(MathPow(10,-degree),degree);
if((maxv-minv)/stepv<10)
stepv/=10.;
}
|