Какие это такие запросы? Вы свой запрос перечитайте, запрос так запрос, - я на первом предложении то застрял, а развитие мысли "какие после каких бывают" добил меня окончательно.
PS: Жаль, что у Вас нет компаса. Хорошая штука - стороны света разные там показывает, направления всякие ...
Какие это такие запросы? Вы свой запрос перечитайте, запрос так запрос, - я на первом предложении то застрял, а развитие мысли "какие после каких бывают" добил меня окончательно.
PS: Жаль, что у Вас нет компаса. Хорошая штука - стороны света разные там показывает, направления всякие ...
好吧,我没什么可说的,唉。:(
Ну мне сказать тут нечего, увы. :(
关于罗盘?- 这是个笑话,我想它会适合你的 "心理类型"。:о)
Алексей, тебя мое решение устраивает ?
Думаешь для 7-го это слишком круто (не общий, а частный случай 25 одноклассников) ?
是的,对于7岁的孩子来说,这有点太贵了。但它是初级的,这很好。
Yurixx 写道(a)>> 两个元素必须有相同的值。
不难发现,在N=26的情况下(即班上没有零关系的学生),这个重复数=13。
我唯一不明白的是为什么是13而不是14或2。你和你的顺序分区程序使我的大脑软化了--但也许这就是你应该寻找的解释,为什么它是13:)
顺便说一句,你使用了迪里切特原理,却没有说出它的名字。
А почему так?
好问题)
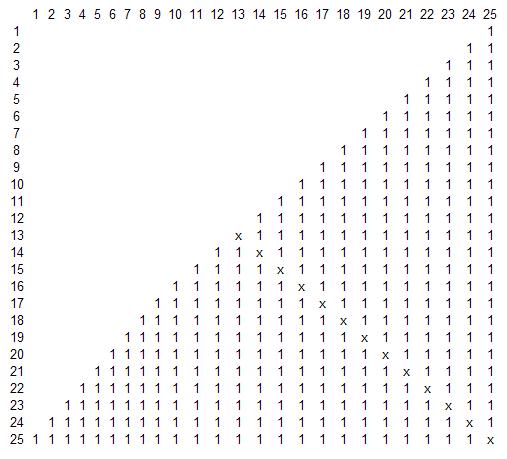
照片是(从1到25)。
对角线xxx,没有人和自己是朋友,有必要做的是Petya,所以它是可见的十三次))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
在0到24的情况下,你可以忽略一个同学,得到24*24和12个X的平方。
如果是奇数大小的正方形,对角线=(N+1)/2,如果是偶数大小的正方形,则为N/2。
你可以把它看作是有Petya和没有Petya的班级中友谊的差异)。
这听起来不像是一个严格的证明。这更像是一个指点江山的图解,没有明确的理由,到底是12还是13。好吧,让我们考虑一下。
我唯一不明白的是为什么是13而不是14或2。你和你的顺序分区程序软化了我的思想--但也许这就是你应该寻找解释的地方,为什么是13:)
顺便说一句,你使用了迪里切特原理,却没有说出它的名字。
关键是,在这种分区下(而且它只服从一个原则--每个人都有不同数量的朋友,因此相当普遍)Petya根本不参与。他是26名学生中的一员,与其他人绝对平等。结果发现,每个人都不可能有不同数量的朋友--从1到N-1的系列不可能连续编号为N个不同的数字(这在最后的证明中)。因此,两个学生的朋友数量必须相同。而这两个学生在这一排的中心位置彼此相邻。因此,事实证明,Petya一定是这两个中的一个。只是在这种情况下,其他人都有不同数量的朋友。任何其他标记都不能满足这一条件。
如果你尝试在中心地带进行手工分区,你会看到自己的情况。
斯旺的 表格说明了这一点。
我希望我对你的问题理解正确。
我想我并没有使用迪里切特原理,而是提供了一个关于其特例的基本证明。
我个人很喜欢它。
它很优雅。
这让我想起了关于灵活的小高斯和老师的寓言故事,老师给全班同学布置了从1到99的加法任务,并打算离开一段时间--而孩子们正在加法。
他们已经知道乘法,但重复是学习之母。
高斯骗过了老师--答案马上就出来了。
;)
Swetten у нас самая дружелюбная.
:)
В коллективе из N сотрудников не может быть ситуации когда у каждого разное количество друзей
А вот если добавить - "у двух возможно одинаковое количество друзей" тогда нет проблем
Остается обозвать Петей одного из этих двух
是的,这几乎是正确的。
如果你合法地阅读这个问题,那么彼得可能和其他的人有相同数量的朋友。
我告诉过你--这个问题是不正确的--通过任何条件的阅读。我 也许可以 证明这一点,而且是以各种方式。但我还不会.....。