RSA Library for asymmetric encryption in MQL5 - libreria per MetaTrader 5

Example Usages

Raw RSA Implementation:

This simple example demonstrates how the RSA encryption could be implemented. First, create an instance of the RSA class then prepare your message (the data that you want to encrypt) as uchar[], where each element is one byte. Finally, call EncryptPKCS1v15 (plain, cipher) to do the encryption. The result is as a char array and stored in cipherData[]:

//+------------------------------------------------------------------+
//|                                           RSA_Implementation.mq5 |
//|                                Vahid Irak , SiavashNourmohammadi |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Vahid Irak , SiavashNourmohammadi"
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <RSA.mqh>

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
 

   MQL5_RSA rsa;
   //public key is consisted of modulus and exponent 
   string modulusHex = "f5746ac76303ef6b74ed9f6914c8f848d55ade9b16d0014d021c12fb1b0f8a63b6409b15b887735b9f08d1e2b96c331b7793b4bcae04e94187e8a08e813251bcedaedd597a14bed263bbe7e0f6406e9d8dad526bc8aecf879afe2eb4fa1d88d707c48e9675b5d3fdb5fea2473b00dccb7b5066c8bed8515fd6f389b9f7f02c5f"; // Your modulus in hex
   int exponent = 65537;

  
/* original format of public key and private key equivalent to the above hex format keys . 
   
   -----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQD1dGrHYwPva3Ttn2kUyPhI1Vre
mxbQAU0CHBL7Gw+KY7ZAmxW4h3NbnwjR4rlsMxt3k7S8rgTpQYfooI6BMlG87a7d
WXoUvtJju+fg9kBunY2tUmvIrs+Hmv4utPodiNcHxI6WdbXT/bX+okc7ANzLe1Bm
yL7YUV/W84m59/AsXwIDAQAB
-----END PUBLIC KEY-----
   
   
   -----BEGIN RSA PRIVATE KEY-----
MIICXAIBAAKBgQD1dGrHYwPva3Ttn2kUyPhI1VremxbQAU0CHBL7Gw+KY7ZAmxW4
h3NbnwjR4rlsMxt3k7S8rgTpQYfooI6BMlG87a7dWXoUvtJju+fg9kBunY2tUmvI
rs+Hmv4utPodiNcHxI6WdbXT/bX+okc7ANzLe1BmyL7YUV/W84m59/AsXwIDAQAB
AoGAT5slMmtbkF/SeWq1Aue3FrATm5TDDk0Ns7x1L3l0TdbO+h8SKVnMwQ9QJfoZ
Vw0wQFToTjVGJHx7XqgL77zpIvF9TJMsb5sASMJeeuGK1W6zGfkL70DWPEhNzOVf
K8bBezdDt0DWaGpOH5f59vYgtmKbnL/fWb+wQoVAXYQDLZECQQD8IcOZs7OrsCIs
grHBzuW8plJmHxd1fIiOcDsA4jAr2daeZ0tg8UhMY4nQVLOEBtYtBTGmbrt9ZlEe
1gsWA13HAkEA+ThtzNGVPrw4Zg58r2Hgo2xvjZKnUHSM0Ktr+ZynHDM17wQOxN7V
zeJvKHp5ITs4Sr2iq6DA1XGpUayUcN6cqQJBANGVC2/fddGYhr+zICm3XzbSlpn2
7Fwn2ad1WUahvmMlIAbqXDlIN83vy+YWEmcD+9LOh3gOgeF6RKI6UFrLD48CQHE8
9JcF+7w/pZipqHnADWP0F1PKeP+TlZAS88K9LSkhE7aAr31AiwE7i6pmy7cPw2oi
dFFrf3L8bCTSN7h5TdECQGoF6kvT209ImVT8PbBAXs9mE+/9P3nKaE/3kuo7AJBr
+tDPu9bXxfjFl/bgxBJv37bavVviT4x06eO/kwxpOkk=
-----END RSA PRIVATE KEY--
   
   */
   
   rsa.Init(modulusHex, exponent);

   string plainText = "Hello RSA!";
   uchar plainData[];
   StringToCharArray(plainText, plainData, 0, StringLen(plainText));

   uchar cipherData[];
   if(rsa.EncryptPKCS1v15(plainData, cipherData))
   {
      string base64Cipher = rsa.Base64Encode(cipherData);
      Print("Encrypted: ", base64Cipher);
   }
   else
   {
      Print("Encryption failed!");
   }

   return(INIT_SUCCEEDED);
  }

The result of encryption is printed into the console. This result will change every time due to padding behavior

string chipertext = "Y9k1Qjxnh/IiQZeeGkf+8Og5iU6OQh8JUVUpc9E4bZTlGHRZPc/xqFUQxE8vTjQRMuB3hNoaT5GLmv7VabwZoRiplAbBR+KiD5bfLQ+CvqTe1W8g4C+7aLTurj0LY6pjiuyZKnM8wYolxRKBkXVMs8gy12TbD8gcH//1rZhrHdo=";

Using RSA + AES in a real project:

In real-world cryptographic systems—including secure trading platforms, web servers, and distributed APIs—RSA is rarely used to encrypt large data directly. RSA encryption is computationally intensive and limited by key size, making it unsuitable for large payloads. To achieve both high-performance and strong security, RSA is typically combined with AES in a hybrid encryption model that leverages the strengths of both algorithms.

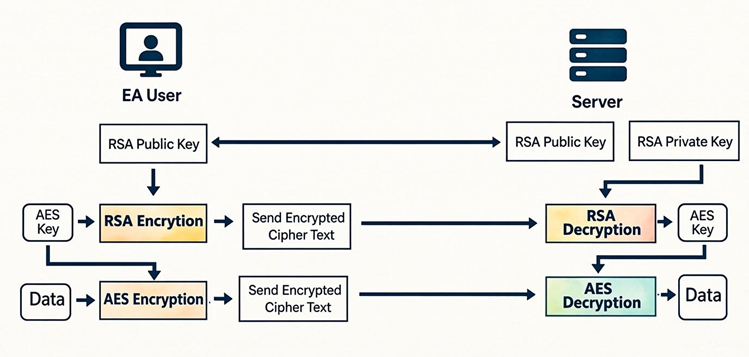
The hybrid encryption workflow generally follows these steps:

1. Generate a random AES session key (for example, 128 or 256 bits).
2. Encrypt this AES key using the RSA public key. Only the owner of the corresponding private key can later decrypt it.
3. Encrypt the actual data payload using AES — a fast, symmetric cipher ideal for large messages or files.
4. Transmit both components together:
   • The AES-encrypted data (fast and compact).
   • The RSA-encrypted AES key (small but secure).

This approach combines the advantages of both algorithms. RSA enables secure key exchange between two parties without a pre-shared secret, while AES provides high-speed encryption for the actual data. In this model, RSA functions as the key protector, and AES functions as the data protector. Together, they form the foundation of modern secure communication protocols, such as SSL/TLS, HTTPS, and VPN tunnels.

In the context of MQL5, this strategy allows developers to secure communications between Expert Advisors, indicators, and external servers, even when using standard HTTP or socket connections. The RSA class implemented in this article can be used to encrypt the AES key, while the built-in MQL5 functions CryptEncode() and CryptDecode() handle AES encryption and decryption of the actual message.

This enables a fully self-contained security layer inside MetaTrader 5, effectively creating a lightweight version of “HTTPS over HTTP.” It can be used to protect sensitive data, such as trading commands, authentication credentials, or configuration messages, without relying on external encryption libraries or DLLs.

Step 1—Server generates RSA public key:

Use Python, Java, OpenSSL, or any backend environment to generate modulus (hex string), exponent (normally 65537), and private key (kept on your server side).

The EA will only use the public values. Do not expose the private key to the client side.

modulusHex = "A1B2C3…";
exponent   = 65537;

Step 2— EA creates an RSA instance and loads the key:

#include <RSA.mqh>  

MQL5_RSA rsa;  
rsa.Init(modulusHex, exponent);

Step 3 — EA prepares a request message:

Example payload can be a login request containing:EA ID, account number, and timestamp. Make a proper JSON string for your request. You can use any third-party library to make the JSON string. The snippet below demonstrates what the expected JSON string should look like:

string json =
   "{\"cmd\":\"login\","
   "\"account\":" + IntegerToString(AccountInfoInteger(ACCOUNT_LOGIN)) + ","
   "\"ts\":" + IntegerToString((int)TimeCurrent()) + ","
   "}"; 
uchar plain[];
StringToCharArray(json, plain, 0, StringLen(json));

Step 4 — EA encrypts the AES session key with RSA:

The AES key used for the rest of the session:

uchar aesKey[];
GenerateAESKey(aesKey);   // 16 random bytes (AES-128)
uchar encryptedAes[];
rsa.EncryptPKCS1v15(aesKey, encryptedAes);
string encryptedAesBase64 = rsa.Base64Encode(encryptedAes);

Step 5 — EA encrypts the actual data with AES:

uchar encryptedPayload[];
CryptEncode(CRYPT_AES128, plain, aesKey, encryptedPayload);
string payloadBase64 = CryptBase64Encode(encryptedPayload);

Step 6 —EA sends everything to the server:

string body =
   "{\"key\":\"" + encryptedAesBase64 + "\","
   + "\"data\":\"" + payloadBase64 + "\"}";

string result;
char headers[];
int status = WebRequest("POST", url, headers, 5000, body, result);

Step 7 — Server-side decryption (conceptual):

On the server, first perform base64-decode for the RSA-encrypted AES key, then decrypt AES key using the private RSA key. Once the AES key is recovered, it can be used to decrypt the data payload. Since the AES key is randomly generated for each session, each message remains unique and secure, even if an attacker intercepts the traffic. This mechanism effectively establishes a secure session, analogous to a simplified HTTPS tunnel.

Step 8 — Client side decrypts server response:

uchar responseCipher[];
CryptBase64Decode(result, responseCipher);
uchar responsePlain[];
CryptDecode(CRYPT_AES128, responseCipher, aesKey, responsePlain);

string serverReply = CharArrayToString(responsePlain);
Print("Server replied: ", serverReply);

By following these steps, real-world cryptography can be implemented directly within the MetaTrader 5 environment, resulting in a reliable and fully portable solution for end users. You can read this article to get more information about RSA encryption system.

The RSA library

Here is the RSA class source code. You can also use this library for big Integer arithmetic.

//+------------------------------------------------------------------+
//|                                                          RSA.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"


// MQL5_RSA_fixed.mq5
// Fixed and documented pure-MQL5 RSA implementation (encryption PKCS#1 v1.5)
// TL;DR: The original logic bug was in HexToBytes (it appended character codes, not hex chars)
// and the modulo routine was extremely slow (repeated single-subtractions). I fixed HexToBytes,
// added a byte-shift long-division style Mod implementation, seeded the RNG for padding,
// and made minor robustness improvements.

/*
Plan / Pseudocode:
1. Initialization
   - Convert hex modulus string to byte array correctly
   - Normalize (remove leading zeros)
   - Store exponent
2. PKCS#1 v1.5 padding
   - Check max length
   - Build EM: 0x00 || 0x02 || PS (non-zero random bytes) || 0x00 || M
   - Seed RNG once in constructor
3. Big-integer helpers (big-endian byte arrays)
   - Normalize: strip leading zeros
   - Compare: compare lengths then lexicographically
   - SubtractInPlace: a = a - b (assume a >= b), big-endian
   - LeftShiftBytes: shift by whole bytes (append zeros at end)
   - Multiply: schoolbook, big-endian
   - MulMod: multiply then reduce modulo
   - Mod: implement long-division by shifting divisor to align with remainder and subtracting multiples (fast enough for modest key sizes)
4. ModExp: fast exponentiation using MulMod
5. Base64 encoding helper (unchanged logic)

Notes on correctness:
- Arrays are big-endian: index 0 = most-significant byte
- Functions avoid destructive changes to external arrays by copying when needed
- RNG seeded with MathSrand for unpredictable padding
*/

#property strict

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class MQL5_RSA
  {
private:
   uchar             modulus[]; // modulus (n), big-endian
   int               exponent;  // public exponent (e)
   bool              debugMode;

public:
                     MQL5_RSA(bool debug=false)
     {
      debugMode = debug;
      // seed RNG once
      MathSrand((int)TimeLocal());
     }

   void              Init(string modulusHex, int e)
     {
      ArrayResize(modulus,0);
      if(debugMode)
         PrintFormat("Init: modulus hex len=%d, e=%d", StringLen(modulusHex), e);
      HexToBytes(modulusHex, modulus); // fixed conversion
      Normalize(modulus);
      exponent = e;
      if(debugMode)
         PrintFormat("Init completed: modulus bytes=%d", ArraySize(modulus));
     }

   bool              EncryptPKCS1v15(uchar &plain[], uchar &cipher[])
     {
      int k = ArraySize(modulus);
      int mlen = ArraySize(plain);

      if(debugMode)
         PrintFormat("Encrypt: key bytes=%d, plain=%d, max=%d", k, mlen, k-11);

      if(mlen > k - 11)
        {
         if(debugMode)
            Print("Error: data too large for key");
         return false;
        }

      // build EM
      uchar em[];
      ArrayResize(em, k);
      ArrayInitialize(em, 0);
      em[0] = 0x00;
      em[1] = 0x02;

      int psLen = k - mlen - 3;
      for(int i=0;i<psLen;i++)
        {
         uchar b=0;
         // ensure non-zero padding byte
         do
           {
            b = (uchar)(MathRand() % 256);
           }
         while(b==0);
         em[2+i] = b;
        }
      em[2+psLen] = 0x00;
      // copy message into em at position 3+psLen
      ArrayCopy(em, plain, 3+psLen, 0, mlen);

      if(debugMode)
         Print("EM constructed");

      // modular exponentiation
      uchar cBig[];
      if(!ModExp(em, exponent, modulus, cBig))
        {
         if(debugMode)
            Print("ModExp failed");
         return false;
        }

      // ensure ciphertext length matches modulus length (leading zeros)
      int clen = ArraySize(cBig);
      ArrayResize(cipher, k);
      if(clen < k)
        {
         // zero-fill
         ArrayInitialize(cipher, 0);
         ArrayCopy(cipher, cBig, k-clen, 0, clen);
        }
      else
        {
         ArrayCopy(cipher, cBig);
        }

      if(debugMode)
         Print("Encryption finished");
      return true;
     }

   string            Base64Encode(uchar &data[])
     {
      string chars = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/";
      int len = ArraySize(data);
      string out = "";

      for(int i=0;i<len;i+=3)
        {
         int b0 = data[i];
         int b1 = (i+1 < len) ? data[i+1] : 0;
         int b2 = (i+2 < len) ? data[i+2] : 0;
         int val = (b0 << 16) | (b1 << 8) | b2;

         out += StringSubstr(chars, (val >> 18) & 0x3F, 1);
         out += StringSubstr(chars, (val >> 12) & 0x3F, 1);
         out += (i+1 < len) ? StringSubstr(chars, (val >> 6) & 0x3F, 1) : "=";
         out += (i+2 < len) ? StringSubstr(chars, val & 0x3F, 1) : "=";
        }

      return out;
     }

private:
   // --- helpers ---
  // Correct HexToBytes: keeps only hex chars and converts pairs -> bytes
// Convert single hex char → nibble (0-15)
int HexNibble(ushort c)
{
   if(c >= '0' && c <= '9') return (int)(c - '0');
   if(c >= 'A' && c <= 'F') return (int)(c - 'A' + 10);
   if(c >= 'a' && c <= 'f') return (int)(c - 'a' + 10);
   return 0;
}

// Correct HexToBytes for MQL5
void HexToBytes(string hex, uchar &out[])
{
   string clean = "";
   int L = StringLen(hex);

   // keep only hex chars
   for(int i = 0; i < L; i++)
   {
      ushort c = StringGetCharacter(hex, i);
      if((c >= '0' && c <= '9') || (c >= 'A' && c <= 'F') || (c >= 'a' && c <= 'f'))
         clean += StringSubstr(hex, i, 1);
   }

   // ensure even length
   if(StringLen(clean) % 2 == 1)
      clean = "0" + clean;

   int n = StringLen(clean) / 2;
   ArrayResize(out, n);

   for(int i = 0; i < n; i++)
   {
      ushort c1 = StringGetCharacter(clean, i*2);
      ushort c2 = StringGetCharacter(clean, i*2+1);

      int high = HexNibble(c1);
      int low  = HexNibble(c2);

      out[i] = (uchar)((high << 4) | low);
   }
}


   void              Normalize(uchar &a[])
     {
      int size = ArraySize(a);
      int leading = 0;
      while(leading < size && a[leading] == 0)
         leading++;
      if(leading == 0)
         return;
      int newSize = size - leading;
      if(newSize <= 0)
        {
         ArrayResize(a, 0);
         return;
        }
      uchar temp[];
      ArrayResize(temp, newSize);
      ArrayCopy(temp, a, 0, leading, newSize);
      ArrayResize(a, newSize);
      ArrayCopy(a, temp);
     }

   int               Compare(const uchar &a_in[], const uchar &b_in[])
     {
      // non-destructive compare
      uchar a[];
      ArrayCopy(a, a_in);
      uchar b[];
      ArrayCopy(b, b_in);
      Normalize(a);
      Normalize(b);
      int na = ArraySize(a), nb = ArraySize(b);
      if(na > nb)
         return 1;
      if(na < nb)
         return -1;
      for(int i=0;i<na;i++)
        {
         if(a[i] > b[i])
            return 1;
         if(a[i] < b[i])
            return -1;
        }
      return 0;
     }

   void              SubtractInPlace(uchar &a[], const uchar &b[])
     {
      // assume a >= b; big-endian arrays
      int na = ArraySize(a);
      int nb = ArraySize(b);
      int borrow = 0;
      for(int i=0;i<na;i++)
        {
         int ai = (int)a[na-1-i];
         int bi = (i < nb) ? (int)b[nb-1-i] : 0;
         int diff = ai - bi - borrow;
         if(diff < 0)
           {
            diff += 256;
            borrow = 1;
           }
         else
            borrow = 0;
         a[na-1-i] = (uchar)diff;
        }
      Normalize(a);
     }

   void              LeftShiftBytes(const uchar &in[], int shiftBytes, uchar &out[])
     {
      int n = ArraySize(in);
      if(n==0 || shiftBytes==0)
        {
         ArrayCopy(out, in);
         return;
        }
      ArrayResize(out, n + shiftBytes);
      for(int i=0;i<n;i++)
         out[i] = in[i];
      for(int i=n;i<n+shiftBytes;i++)
         out[i] = 0; // append zeros at LSB side
     }

   void              Multiply(const uchar &a[], const uchar &b[], uchar &result[])
     {
      int na = ArraySize(a);
      int nb = ArraySize(b);
      if(na==0 || nb==0)
        {
         ArrayResize(result,0);
         return;
        }
      int nRes = na + nb;
      int temp[];
      ArrayResize(temp, nRes);
      ArrayInitialize(temp,0);

      for(int i=na-1;i>=0;i--)
        {
         int carry = 0;
         for(int j=nb-1;j>=0;j--)
           {
            int prod = (int)a[i] * (int)b[j] + temp[i+j+1] + carry;
            temp[i+j+1] = prod % 256;
            carry = prod / 256;
           }
         temp[i] += carry;
        }

      ArrayResize(result, nRes);
      for(int i=0;i<nRes;i++)
         result[i] = (uchar)temp[i];
      Normalize(result);
     }

   
// Big integer modulo using long division (fast)
bool Mod(const uchar &a_in[], const uchar &m_in[], uchar &result[])
{
   if(ArraySize(m_in) == 0) return false;

   // Normalize inputs
   uchar dividend[]; ArrayCopy(dividend, a_in); Normalize(dividend);
   uchar modv[];     ArrayCopy(modv, m_in);   Normalize(modv);

   if(Compare(dividend, modv) < 0)
   {
      ArrayCopy(result, dividend);
      return true;
   }

   int m = ArraySize(dividend);

   // working remainder
   uchar rem[];
   ArrayResize(rem, 0);

   for(int i = 0; i < m; i++)
   {
      // shift left rem by 1 byte and add next dividend byte
      int rlen = ArraySize(rem);
      ArrayResize(rem, rlen + 1);
      rem[rlen] = dividend[i];
      Normalize(rem);

      // subtract modulus while remainder >= modulus
      while(Compare(rem, modv) >= 0)
      {
         SubtractInPlace(rem, modv);
      }
   }

   Normalize(rem);
   ArrayCopy(result, rem);
   return true;
}


bool MulMod(const uchar &a[], const uchar &b[], const uchar &m[], uchar &out[])
{
   uchar product[];
   Multiply(a, b, product);   // standard schoolbook multiply
   return Mod(product, m, out);
}

   bool              ModExp(const uchar &base[], int exp, const uchar &modn[], uchar &result[])
     {
      if(debugMode)
         PrintFormat("ModExp: exp=%d", exp);
      uchar baseCopy[];
      ArrayCopy(baseCopy, base);
      Normalize(baseCopy);
      // reduce base modulo modn
      if(Compare(baseCopy, modn) >= 0)
        {
         if(!Mod(baseCopy, modn, baseCopy))
            return false;
        }

      uchar res[];
      ArrayResize(res,1);
      res[0] = 1;
      Normalize(res);
      uchar basePow[];
      ArrayCopy(basePow, baseCopy);

      int e = exp;
      while(e > 0)
        {
         if((e & 1) == 1)
           {
            uchar tmp[];
            if(!MulMod(res, basePow, modn, tmp))
               return false;
            ArrayCopy(res, tmp);
           }
         e >>= 1;
         if(e > 0)
           {
            uchar tmp2[];
            if(!MulMod(basePow, basePow, modn, tmp2))
               return false;
            ArrayCopy(basePow, tmp2);
           }
        }

      Normalize(res);
      ArrayCopy(result, res);
      return true;
     }
  };




/*
Usage notes:
- Create instance: MQL5_RSA rsa(true); rsa.Init("<hex modulus>", 65537);
- Prepare plaintext as uchar[] where each element is one byte.
- Call EncryptPKCS1v15(plain, cipher).
*/

// Example usage:
/*
void OnStart()
{
   MQL5_RSA rsa;
   string modulusHex = "A1B2C3D4E5F6..."; // Your modulus in hex
   int exponent = 65537;

   rsa.Init(modulusHex, exponent);

   string plainText = "Hello RSA!";
   uchar plainData[];
   StringToCharArray(plainText, plainData, 0, StringLen(plainText));

   uchar cipherData[];
   if(rsa.EncryptPKCS1v15(plainData, cipherData))
   {
      string base64Cipher = rsa.Base64Encode(cipherData);
      Print("Encrypted: ", base64Cipher);
   }
   else
   {
      Print("Encryption failed!");
   }
}
*/
//+------------------------------------------------------------------+