В статье есть одно серьёзное противоречие. С одной стороны, мы установили с помощью индикатора трендовости, что реальной курс – трендовый. С другой стороны, мы утверждаем, что реальный курс колеблется в границах горизонтального фундаментального канала. А горизонтальный канал – очень сильный признак антитрендовости.
Es gibt hier keinen Widerspruch. Das grundlegende Gesetz von Angebot und Nachfrage sagt diese Effekte voraus. Der springende Punkt ist, dass das gesamte Modell dynamisch betrachtet werden sollte, d.h. die Grenzen des horizontalen Fundamentalkanals ändern sich mit der Zeit. Um zu verstehen, wovon ich spreche, ist es notwendig, zunächst ein klassisches statisches Angebots-Nachfrage-Modell (für das "Hier und Jetzt") zu betrachten:
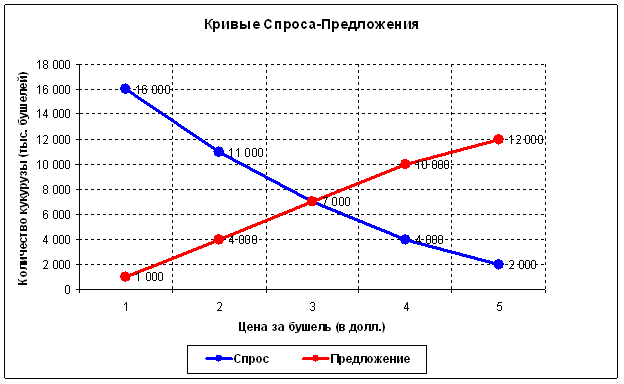
Das heißt, zu jedem Zeitpunkt gibt es nur einen maximal effizienten Austauschpunkt für ein Gut (in diesem Fall 7000 Scheffel zu einem Preis von 3 Dollar). An allen anderen Punkten werden weniger Güter für weniger Geld getauscht. Die gesamtwirtschaftliche Situation ändert sich ständig, was bedeutet, dass sich auch dieser effiziente Tauschpunkt selbst ändert. Der Markt ist jedoch effizient, und seine Hauptaufgabe besteht darin, ständig nach einem solchen Punkt oder dem Gleichgewichtspreis zu suchen ("alle, die kaufen wollten - kauften, alle, die verkaufen wollten - verkauften"). Das Volumen an diesem Punkt sollte groß sein, weil an diesem Punkt die maximale Menge an Waren ausgetauscht wird. Der Markt braucht Zeit, um ein solches Volumen zu realisieren. Diese Theorie sagt den Effekt der Volumenakkumulation voraus:
Der Markt befindet sich die meiste Zeit in der Konsolidierungsphase (im Bereich seiner maximalen Effizienz).
Die Weltwirtschaft als Ganzes entwickelt sich jedoch ständig weiter. Neue Technologien tauchen auf, der Lebensstandard verbessert sich. Infolgedessen werden einerseits immer mehr Waren und Dienstleistungen benötigt, und andererseits ermöglicht der wissenschaftliche und technische Fortschritt die Herstellung von immer mehr Waren und Dienstleistungen. Die Liquidität nimmt mit der Zeit zu. Das Volumen der Weltmärkte muss wachsen, und infolgedessen nimmt ihre Volatilität zu, so dass das Ausmaß von Krisen zusammenbricht. Da die Nachfrage mit der Zeit zunimmt, steigt der Preis. Gleichzeitig versorgt der wissenschaftliche und technische Fortschritt diese Nachfrage mit immer mehr Waren und Dienstleistungen. Infolgedessen verschiebt sich der Gleichgewichtspunkt im Allgemeinen im Laufe der Zeit nach oben und nach rechts. Der Markt, der ständig um diesen Punkt herumwandert, wird im Allgemeinen ebenfalls wachsen (er neigt zu hohen Preisen).

Daher rührt dieser "Trend-Effekt". Das alles lässt sich mathematisch so gut durchrechnen, dass es einfach atemberaubend ist. Auf jeden Fall sollten wirtschaftliche Effekte die mathematischen Abhängigkeiten erklären, aber keinesfalls umgekehrt.
Es gibt eine Ungenauigkeit in dem Artikel. Wenn wir einen betrunkenen Seemann als Analogie nehmen, dann ist die Größe des Schritts unterschiedlich. Grob gesagt ist ein Schritt 80 cm lang, wenn man sich von der Kneipe wegbewegt, ein Schritt zurück (zur Kneipe) 60 cm. Der Trend ist der gleiche, es ist auch bekannt, dass die Abwärtsbewegung des Marktes schneller ist als die Aufwärtsbewegung. Und in dem Artikel sind alle Schritte die gleichen +1 oder -1.
Dieses Modell kann also nicht als angemessen betrachtet werden. Es handelt sich lediglich um eine Münze, deren Verteilungseigenschaften seit langem bekannt und untersucht sind.
Der Artikel enthält eine Ungenauigkeit. Wenn wir den betrunkenen Seemann als Analogie nehmen, dann ist die Größe des Schritts unterschiedlich. Grob gesagt ist 1 Schritt 80 cm lang, wenn man sich von der Kneipe weg bewegt, der Schritt zurück (zur Kneipe) 60 cm. Der Trend ist der gleiche, es ist auch bekannt, dass die Abwärtsbewegung des Marktes schneller ist als die Aufwärtsbewegung. Und in dem Artikel sind alle Schritte die gleichen +1 oder -1".
Die Münze hat ein kontinuierliches Analogon - das Modell der geometrischen Brownschen Bewegung. Es wird hier beschrieben http://algoritmus.ru/?p=2889.
"Stochastischer Ansatz zur Lösung von Problemen des algorithmischen Handels".
Autoren: Arsen Yakovlev, Grigory Franguridi
Veröffentlicht: Zeitschrift "D-Shtrich" Nr. 16/6 September 2010
Dieser Artikel enthält die gleichen Ideen wie mein Artikel, nur mehr Mathematik. Ob man ein diskretes oder kontinuierliches Modell nimmt, ist Geschmackssache. Sie sind identisch. Nur hat das eine Modell Integrale und das andere Summen. Und das Münzmodell wird bereits von Schülern verstanden, während das kontinuierliche Modell nur von Studenten verstanden wird.
"Es ist auch bekannt, dass die Abwärtsbewegung des Marktes schneller ist als die Aufwärtsbewegung" - das ist für mich sehr interessant - können Sie mir einen Link zu der Forschung/dem Artikel geben - ich brauche ihn für die Selbstbildung.
"Dieses Modell kann also in keiner Weise als angemessen betrachtet werden. Es handelt sich lediglich um eine Münze, deren Verteilungseigenschaften seit langem bekannt sind und untersucht wurden." - Kein Modell beschreibt die Realität zu 100 Prozent adäquat. Das gilt auch für den Münzkurs als Marktmodell. Deshalb mussten wir ein Modell einer Münze mit einem Trend erfinden, um dem Markt besser gerecht zu werden.
- 2010.09.13
- val
- algoritmus.ru
Warum genau eine Münze? Sie hat zwei Seiten - was spiegeln sie wider? Nur eine ideale zufällige Wanderung auf einer geraden Linie (analog - oben, unten), d.h. eindimensional. Der Preis kann einen anderen Zustand annehmen - flach, d.h. er ist bereits eine Münze mit drei Seiten, d.h. wir haben einen 2-dimensionalen Random Walk. Aus den obigen Diagrammen können wir ersehen, dass ein solcher Marktzustand praktisch nicht modelliert wird - wir können keinen harten Flat sehen.
Die gelbe Kurve in Abbildung 2 kommt einer Abflachung am nächsten. Die engste Fläche erhält man, wenn man den Parameter a=-0,5 nimmt. Dann erhalten wir eine horizontale Linie +1 -1 +1 -1 -1 +1 -1 -1 ...... Zwei Seiten der Medaille reichen also aus, um ein Flat zu beschreiben. Übrigens wird "flach" im Sinne des Artikels als "Anti-Trend" bezeichnet.
Aber dann wird das ganze Diagramm horizontaler, wenn ich das richtig verstehe, und auf dem realen Markt kann es sowohl einen scharfen Trend als auch ein hartes Flat geben, d.h. diese Phänomene sind unabhängig. Unabhängigkeit bedeutet, dass es eine dritte Seite der Medaille geben muss. Ganz einfach, der Markt wandert auf der Ebene, weil der Faktor Zeit wandert, und die Münze hat ein eindimensionales Modell der Wanderung, und eine einfache (ohne Wanderung) Sweep dieses Modells für die Zeit ist nicht ganz korrekt. Aber trotzdem ist dieser Artikel sehr nützlich.
Genau richtig, in der Münze Modell mit einem Trend, trendiness wird als konstant über die gesamte Lebensdauer des Marktes. Und wie der Trendindikator für den Realkurs zeigt, ändert sich die Trendhaftigkeit ständig. Und nur im Durchschnitt über einen langen Zeitraum (Jahre) wird die Tendenz als konstant gemessen.
Damit das Modell "Münzkurs mit Trend" dem Markt entspricht, kann man es verkomplizieren. Man kann den Parameter "a" chaotisch zeitabhängig machen oder etwas anderes erfinden. Das ist eine kreative Sache. Streng genommen ist es nicht nötig, eine zweite Dimension einzuführen, aber wenn man möchte, kann man neben "a" einen zweiten chaotischen Multiplikator hinzufügen.
Ein einfaches Modell mit konstantem Trend wird benötigt, um zum Beispiel diesen Indikator New Moving Mini-Max Technical Analysis Indicator und seine Implementierung in MQL5 zu testen . Es ist nicht realistisch, mit einem solchen Indikator auf dem realen Kurs zu arbeiten, aber es wäre eine schöne Sache, ihn an einem einfachen Modell mit konstantem Trend zu testen.
...Ob man sich für ein diskretes oder ein kontinuierliches Modell entscheidet, ist eine Frage des Geschmacks. Sie sind identisch. Nur hat das eine Modell Integrale und das andere Summen. Und das Münzmodell wird schon von Schülern verstanden, das kontinuierliche Modell nur von Studenten...
Und genau da liegt der Fehler.
1. Der Übergang vom kontinuierlichen Modell zum diskreten Modell muss richtig gemacht werden.
2. beide Modelle können gleich sein (kontinuierlich und diskret), aber es ist notwendig, die Bedingung zu erfüllen, dass der Schritt in + und in - der gleiche sein muss. Seine Größe.
3. hat Balken genommen, um zu analysieren, dass Ihre Aussage "Sie sind gleich" wahr wäre. Nur ein Modell hat Integrale und das andere hat Summen." Beweisen Sie, dass alle Balken gleich sind. Können Sie das beweisen?
4. nur ein Chart hat diese Eigenschaft, der Renko-Chart...Sie können ihn durch +1 -1(https://www.mql5.com/de/code/9447#25419) ersetzen.
Danke für den Link zu dem Artikel. Ich habe ihn gelesen. Er schlägt vor, das ARFIMA-Modell zu verwenden, Sie den Random Walk. Dies sind unterschiedliche Modelle. Es wäre interessant, den folgenden Artikel zu lesen, sowohl Ihren als auch den des Autors. Dort wird nachgewiesen, dass die von Ihnen vorgeschlagenen Marktmodelle angemessen sind. Nicht nur in Worten behauptet, sondern mathematisch bewiesen ... und angesichts der Berechnung dieser Zahl ...
H.Y. Gerade viele Menschen begreifen dieses schöne Wort Angemessenheit, wissen aber nicht einmal, wie man sie berechnet. Sie haben in Ihrem Beitrag geschrieben, dass es kein 100% adäquates Modell gibt. Da stimme ich Ihnen voll und ganz zu. Die Frage ist, inwieweit das vorgeschlagene Modell 20, 30 oder 99,999999999%.... dem Markt angemessen ist.
Versuchen Sie, einen Stapel zu modellieren, der Stapel hat eine klare Struktur, der Stapel sieht Aufträge für eine bestimmte Anzahl von Punkten nach oben und unten.
Der Generator durchläuft alle Zellen (es kann sich nicht um +1 -1 handeln, sondern um die Generierung von Zufallsvolumina), und nachdem alle Zellen des Stapels vom Generator durchlaufen wurden, wird berechnet, wohin der mittlere Punkt des Stapels zu verschieben ist.
Und vergessen Sie nicht, SRAND nach der Erzeugung von 32768 Rand neu zu starten, sonst wird Ihre Sequenz wiederholt.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Random Walk und der Trendindikator :
Der Random Walk sieht realen Marktdaten sehr ähnlich, hat aber einige wichtige Besonderheiten. In diesem Beitrag betrachten wir die Besonderheiten des Random Walk, der mithilfe eines Münzwurfs simuliert wird. Für die Analyse der Eigenschaften der Daten wird der Trendindikator entwickelt.
Autor: Гребенев Вячеслав