Die Frage ist also: Wie kann man sie erfinden? Bislang funktioniert das nur in iterativer Form:
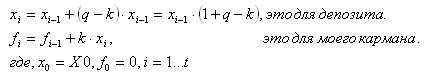
Wir müssen sie in analytischer Form darstellen (als funktionale Abhängigkeit von der Zeit t).
Aha! Dann sieht es so aus:
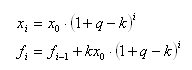
Und der Ausdruck für den Geldbetrag, der über einen Zeitraum von t Monaten abgehoben wird, kann wie folgt geschrieben werden:
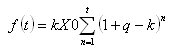
Wenn ja, ist das besser. Was nun? Sie müssen die Menge loswerden...
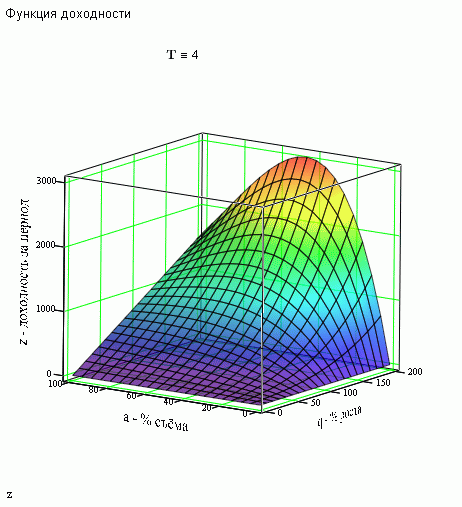
würde etwa so aussehen.
Niemals!...
Können Sie das genauer erläutern? Ich meine in Form einer Formel.
So können Sie wirklich das Optimum in Bezug auf den Prozentsatz der Entfernung sehen!
Wenn ja, ist das besser. Was kommt als Nächstes? Wir müssen die Summe loswerden...
Erinnern Sie sich an die Formel für die Summe der ersten n Terme einer geometrischen Progression
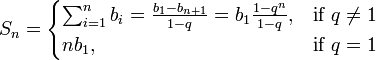
Erinnern Sie sich an die Formel für die Summe der n ersten Terme einer geometrischen Progression
Shaitan! In der Tat, 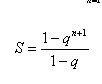 .
.
Der Ausdruck für die Summe der entnommenen Gelder lautet dann schließlich wie folgt:
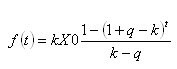
Alles, was bleibt, ist, die zeitliche Ableitung zu nehmen und sie mit Null gleichzusetzen... Ja, ja.
Hallo zusammen!
Ich habe eine Kaution von X0 Rubel für t Monate verwenden dürfen. Jeden Monat erhält die Einlage einen festen Prozentsatz q vom aktuellen Wert der Einlage X. Ich darf jeden Monat einen Prozentsatz k vom Konto abheben, der den Wert von q nicht übersteigt.
Das Problem besteht also darin, den Betrag, der über einen Zeitraum von t Monaten abgehoben wird, zu maximieren.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo zusammen!
Ich habe eine Kaution von X0 Rubel für t Monate verwenden dürfen. Jeden Monat wird ein fester Prozentsatz q des aktuellen Wertes der Einlage X eingezahlt. Ich darf jeden Monat einen Prozentsatz k vom Konto abheben, der den Wert von q nicht übersteigt.
Die Aufgabe besteht also darin, den über einen Zeitraum von t Monaten abgehobenen Geldbetrag zu maximieren. Es liegt auf der Hand, dass die monatliche Abhebung der gesamten aufgelaufenen Zinsen q nicht die beste Option ist, da in diesem Fall die Einlage nicht wächst und bei geringerer Belastung des Kontos der letztendlich abgehobene Betrag größer sein kann... Andererseits darf der Wert von k nicht auf Null sinken, da in diesem Fall auch der abgehobene Geldbetrag auf Null sinkt. Offenbar liegt die Wahrheit irgendwo in der Mitte. Aber wo genau?
Helfen Sie mir, dieses Problem analytisch und allgemein zu lösen.
P.S. Ich habe nicht in einem Zweig von zadacha gepostet , der nicht mit dem Handel zu tun hat, weil das vorgeschlagene Thema mit letzterem zusammenhängt.