Интуитивно понятно, что любой прогноз должен основываться на выявлении некоторых закономерностей в прошлом и применении их к анализу настоящей ситуации. Поэтому необходимо перед началом проведения прогноза выявить какие критерии (это могут быть макро- и микроэкономические данные, торговые данные, оценки общественно-политических событий) оказывали влияние на прогнозируемую величину (возможными прогнозируемыми величинами для данной системы являются доходность и ценовые показатели), т.е. определить прогнозируемую величину и набор критериев прогноза. Хотя существуют методы, позволяющие установить насколько данный критерий влияет на прогнозируемую величину (например вычислить корреляцию), все-таки качество выбора критериев прогноза в основном зависит от опыта и интуиции аналитика. Финансовые рынки являются динамичной, развивающейся системой, поэтому критерий оказывающий влияние на некоторую прогнозируемую величину два месяца назад, совершенно не работает сегодня. Следовательно, нет смысла во-первых формировать большие выборки для проведения прогноза, во-вторых включать в число критериев те данные, которые не оказывали влияние на интересующую величину или не изменяли свое значение в течении периода формирования выборки. Т.о. по окончании данного подготовительного этапа имеются некоторые временные ряды прогнозируемой величины и критериев прогноза, а необходимо по имеющимся критериям на некоторый будущий момент времени определить значение прогнозируемой величины.
В общем случае зависимость
прогнозируемой величины от критериев для данной предметной области достаточно
линейна, поэтому имеет смысл на первом этапе прогноза вычислить эту линейную
составляющую. Т.е. вектор-столбец прогнозируемой величины Y можно представить
как: где линейную составляющую можно представить как
где линейную составляющую можно представить как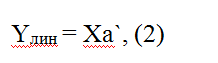 где X - матрица критериев
прогноза,
где X - матрица критериев
прогноза,![]() количество критериев,
количество критериев, ![]() значение j-го критерия на i-ый
момент времени
значение j-го критерия на i-ый
момент времени ![]() параметры линейной функции. Линейная составляющая
может быть вычислена методом наименьших квадратов либо путем прямого
решения матричного уравнения
параметры линейной функции. Линейная составляющая
может быть вычислена методом наименьших квадратов либо путем прямого
решения матричного уравнения ![]() либо одним из методов
безусловной минимизации Т.о. следующей задачей
становится аппроксимация оставшейся нелинейной составляющей некоторой
нелинейной функцией
либо одним из методов
безусловной минимизации Т.о. следующей задачей
становится аппроксимация оставшейся нелинейной составляющей некоторой
нелинейной функцией ![]()
![]() искомые параметры нелинейной
функции. Не трудно заметить, что качество аппроксимации нелинейной
составляющей зависит от качества нахождения параметров a`` и способности Fнелин
аппроксимировать данную зависимость. В данной статье не рассматривается задача
нахождения параметров нелинейной функции,
далее статья будет посвящена проблеме построения моделей, представляющих
нелинейную функцию.
искомые параметры нелинейной
функции. Не трудно заметить, что качество аппроксимации нелинейной
составляющей зависит от качества нахождения параметров a`` и способности Fнелин
аппроксимировать данную зависимость. В данной статье не рассматривается задача
нахождения параметров нелинейной функции,
далее статья будет посвящена проблеме построения моделей, представляющих
нелинейную функцию.
Рассмотрим два пути
формирования аппроксимирующей нелинейной функции: построение нейронной сети,
где нелинейными преобразователями реализуются некоторые непрерывные, везде
дифференцируемые, ограниченные функции и построение нейронной сети, реализующую
некоторую модель, созданную в рамках теории детерминированного хаоса. Т.о.
предоставляется возможность сравнить результаты работы полученных моделей с
аналогичными по сложности моделями, построенными на основе традиционно
применяющихся в нелинейных преобразователях функциях.Функции, традиционно
применяющиеся в нелинейных преобразователях, считаются достаточно хорошими для
аппроксимации фактически любой нелинейной зависимости.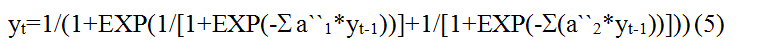 (т.е. нейронная сеть 1-2-1 с
сигмоидным нелинейным преобразователем) реализует функцию
(т.е. нейронная сеть 1-2-1 с
сигмоидным нелинейным преобразователем) реализует функцию ![]() с точностью не ниже 5%. Указанная функция получена при
изучении некоторых хаотических систем, данное исследование показывает, что два
пути решения задачи взаимозаменяемы, встает только вопрос о разнице в
погрешностях.
с точностью не ниже 5%. Указанная функция получена при
изучении некоторых хаотических систем, данное исследование показывает, что два
пути решения задачи взаимозаменяемы, встает только вопрос о разнице в
погрешностях.
. Причины, натолкнувшие на рассмотрение моделей детерминированного хаоса.
В своей часто цитируемой книге "Хаос и порядок на рынке капитала" Петерс говорит, что в рамках теории хаоса можно получить ряд моделей, способных воспроизводить развитие событий на финансовых рынках. В этих моделях предлагается детерминированное объяснение для некоторых аспектов поведения финансовых цен, которые, вообще говоря, считаются случайными и непредсказуемыми. Применение моделей детерминированного хаоса согласуется с принципом ограниченной рациональности Саймона, согласно которому эффективность рынка ограничена в силу ограниченных возможностей человека в обработке информации.Если считать, что изменения цен, вопреки соображениям эффективности на продолжительных отрезках времени, определяются многочисленными и часто нелинейными обратными связями, то на основе теории детерминированного хаоса можно построить улучшенные модели, описывающие влияние прошлого на настоящее. Для рассмотрения полученных моделей функций необходимо хотя бы в самом общем виде изложить основные положения теории детерминированного хаоса, чему и посвящен следующий раздел.
Основные положения теории хаоса.
Под детерминированным хаосом подразумевается нерегулярное или хаотическое движение, порожденное нелинейными системами, для которых динамические законы однозначно определяют эволюцию во времени состояния системы при известной предыстории.
Нелинейность - необходимое, но не достаточное условие возникновения хаотического движения. Наблюдаемое во времени хаотическое поведение возникает не из-за внешних источников шума (их нет в уравнениях Лоренца), не из-за бесконечного числа степеней свободы (в системе Лоренца их только 3) и не из-за неопределенности, связанной с квантовой механикой (рассматриваемые системы чисто классические). Настоящая первопричина нерегулярности определяется свойством нелинейных систем экспоненциально быстро разводить первоначально близкие траектории в ограниченной области фазового пространства. Таким образом, становится практически невозможно предсказать длительное поведение таких нелинейных систем, поскольку реально начальные условия можно задать лишь с конечной точностью, а ошибки экспоненциально возрастают. Если попытаться решить такую нелинейную систему на ЭВМ, результат на все более дальних временах зависит от все большего количества цифр в числах, представляющих начальные условия. А так как числа в иррациональных числах распределены нерегулярно, траектория становится хаотической. Классификация основных систем, которые проявляют детерминированный хаос, приведена на рис.1
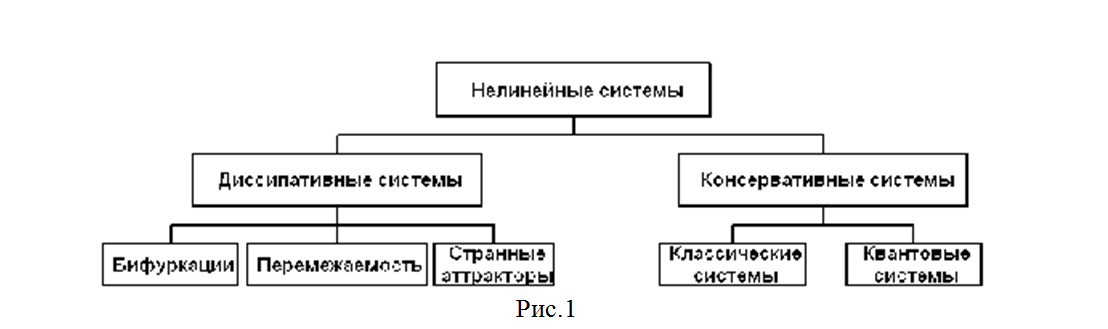
Различают консервативные системы, для которых элемент в фазовом пространстве {x} только изменяет форму, но сохраняет объем и диссипативные системы, для которых объем фазового пространства сокращается с течением времени. Мы рассматривали только диссипативные системы.
Критерии хаотичности системы:1) сигнал "выглядит случайным";
2) в спектре мощности наблюдается широкополосный шум на низких частотах;
3) автокорреляционная функция быстро спадает;
4) сечение Пуанкаре состоит из точек, заполняющих пространство.
Данные системы могут быть описаны системой дифференциальных
уравнений 1-го порядка малой размерности![]() которые автономны (т.е. F не содержит явно времени) и
нелинейны.Поток, описываемый уравнениями движения (7), удобно
исследовать с помощью соответствующего (d - 1)-мерного отображения Пуанкаре:
которые автономны (т.е. F не содержит явно времени) и
нелинейны.Поток, описываемый уравнениями движения (7), удобно
исследовать с помощью соответствующего (d - 1)-мерного отображения Пуанкаре: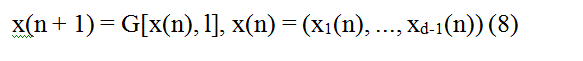
Переход к хаосу через бифуркации.
Данное свойство систем при
переходе к хаосу рассматривается при помощи логистического отображения![]() где r - внешний параметр.Фейгенбаум показал, что при
некоторых ограничениях, переход к хаосу, найденный для данного логистического
отображения, встречается во всех разностных уравнениях первого порядка xn+1
= f(xn),в которых после
соответствующего изменения масштаба f(xn) имеет единственный максимум в
интервале 0 <= xn <= 1. Фейгенбаум установил также, что качественное поведение при
переходе к хаосу описывается универсальными константами (константами
Фейгенбаума a и d), величина которых зависит от
характера максимума.
где r - внешний параметр.Фейгенбаум показал, что при
некоторых ограничениях, переход к хаосу, найденный для данного логистического
отображения, встречается во всех разностных уравнениях первого порядка xn+1
= f(xn),в которых после
соответствующего изменения масштаба f(xn) имеет единственный максимум в
интервале 0 <= xn <= 1. Фейгенбаум установил также, что качественное поведение при
переходе к хаосу описывается универсальными константами (константами
Фейгенбаума a и d), величина которых зависит от
характера максимума.
Описание процесса перехода к хаосу через бифуркацию выглядит следующим образом: число периодических точек отображения fr(x), к которым итерации сходятся, при определенных увеличивающихся значениях параметра rn удваиваются. При r = r¥ число периодических точек становится бесконечным, а за пределами этого (конечного) значения r поведение итераций для большинства r хаотично. Бифуркация лежит в основе механизма последовательного удвоения периодических точек.
Итерации логистического отображения при интегрировании уравнения (9) для разных значений r представлены на рис.2.
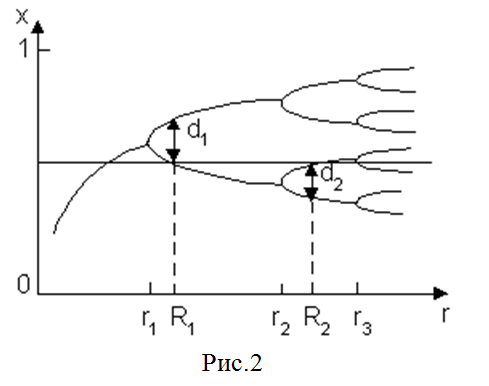
Различают бифуркационный режим при 1 < r < r¥, где показатель Ляпунова l всегда отрицателен (равным нулю он становится лишь в бифуркационных точках rn) и хаотический режим при r¥< r<= 4, где большинство значений l положительно, что указывает на хаотическое поведение. Хаотический режим прерывается r-окнами, где последовательность {fnr(x0)} вновь оказывается в пределе периодической, что соответствует неравенству l<0. При этом имеют место некоторые закономерности, которые не представляется возможным привести в данной статье.
Переход к хаосу через перемежаемость.
Под перемежаемостью понимают такой вид сигнала, в котором случайным образом чередуются длинные регулярные (ламинарные) фазы (так называемые окна) и относительно короткие нерегулярные всплески. При этом число хаотических всплесков нарастает при увеличении внешнего параметра, а это означает, что перемежаемость представляет собой непрерывный переход от регулярного движения к хаотическому.
Переход к хаосу через перемежаемость может быть исследован
с помощью модели Лоренца: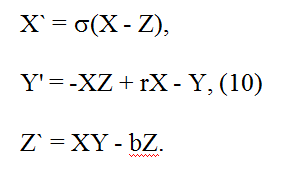
Y-компонента ведет себя следующим образом. При r < rc реализация Y(t) представляет собой устойчивое периодическое движение. При превышении порога rc колебания прерываются хаотическими всплесками, которые с ростом r становятся все более частыми, пока движение полностью не хаотизируется. Объясняется это следующим образом. Устойчивым колебаниям при r < rc соответствует устойчивая неподвижная точка на отображении Пуанкаре. При r > rc эта точка становится неустойчивой. Различают три рода перемежаемости, для иллюстрации поведения финансовых рынков используется только перемежаемость первого рода.
Перемежаемость первого рода. Модель Лоренца и логистическое отображение xn+1 = fr(xn) = rxn(1 - xn) относятся именно к этому типу. Отображение имеет вид:
xn+1 = e + xn + uxn2 (11)
Для этого перехода (см. рис.3) характерна обратная
касательная бифуркация, при которой две неподвижные точки (устойчивая и
неустойчивая) сливаются. При r > rc отображение не имеет
устойчивых неподвижных точек. Однако существует некоторая "память" об
исчезнувшей неподвижной точке, так как движение сильно замедляется вблизи xc
и требуется много итераций для того, чтобы пройти через узкий канал между
кривой отображения и биссектрисой. Это приводит к появлению длинных ламинарных
областей при небольшом превышении r над rc. После выхода траектории
из канала начинается хаотический всплеск, который завершится, когда траектория
попадает вновь в окрестность xc и начнется новая регулярная фаза.
При достаточном увеличении r движение полностью хаотизируется. Обратная
касательная бифуркация (в противоположность бифуркации удвоения) представляет
единственный механизм, при котором в логистическом отображении может появиться
нечетное число неподвижных точек. При этом имеют место некоторые
закономерности, которые не представляется возможным привести в данной статье.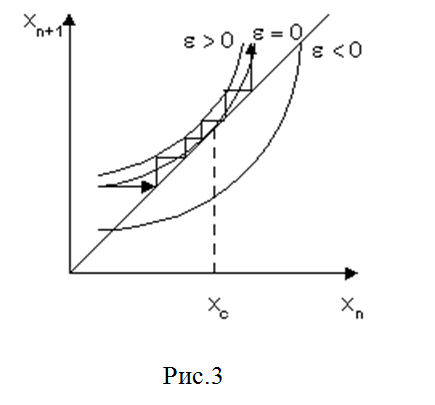
Перемежаемость второго рода. Отображение имеет вид:
rn+1 = (1 + e)rn + urn3 (12)
qn+1 = qn + W
Перемежаемость третьего рода. Отображение имеет вид:
xn+1 = -(1 + e)xn - uxn3 (13)
Понятие странного аттрактора.
Странный аттрактор обладает следующими свойствами:
1) он является аттрактором, т.е. занимает ограниченную область фазового пространства {x}, к которой по истечении большого интервала времени притягиваются все достаточно близкие траектории из так называемой области притяжения. Сам аттрактор состоит как бы из одной траектории, т.е. траектория с течением времени должна пройти через каждую точку аттрактора;
2) чувствителен к начальным условиям, т.е., несмотря на сжатие в объеме, не происходит сокращения длин во всех направлениях и расстояния между первоначально сколь угодно близкими точками на аттракторе через достаточно большое время становятся конечными;
3) аттрактор должен быть структурно устойчивым и типичным, т.е. малые изменения параметра в F (x = F(x)) изменяют структуру аттрактора непрерывным образом и множество параметров, для которых x = F(x) порождает странный аттрактор, не должно быть множеством меры 0.
Все обнаруженные к настоящему времени странные аттракторы имеют дробную хаусдорфову размерность, при чем по теореме Пуанкаре-Бендикссона размерность порожденных потоками странных аттракторов больше двух. Понятие странного аттрактора не ограниченно диссипативными потоками (x = F(x)): диссипативные отображения (x(n + 1) = G[x(n)]; x(n) = [x1(n), ..., xd(n)) также могут порождать странные аттракторы, при чем теорема Пуанкаре-Бендикссона несправедлива для отображений, т.к. отображения порождают дискретные точки и снимаются ограничения, связанные с непрерывностью.
Странный аттрактор можно наблюдать в случае диссипативного отображения Хенона - это двумерный аналог логистического отображения:
xn+1 = 1 - axn2 + yn (14)
yn+1 = bxn, |b| < 1
или упрощенный одномерный вариант:
xn+1 = 1 - axn2 + bxn-1, |b| < 1 (15)
Одним из важнейших понятий для понимания происхождения странного аттрактора является понятие бифуркаций Хопфа. Простой бифуркацией Хопфа соответствует рождение предельного цикла из неподвижной точки.Биффуркация Хопфа вводит в систему новую основную частоту. Рюэль и Такенс показали, что после двух бифуркаций Хопфа регулярное движение может стать сильно неустойчивым и перейти в хаотическое движение на странном аттракторе. При этом подразумевается, что хаотическое движение становится возможным только после двух бифуркаций Хопфа, когда траектория может выходить в дополнительные измерения, так как двухпериодическое движение соответствует траектории на торе, на котором появление хаоса запрещается теоремой Пуанкаре-Бендикссона. Однако после двух бифуркаций Хопфа появление странного аттрактора не только возможно, но и неизбежно.
Основные пути перехода к хаосу.
В таблице 1 приведен перечень основных путей перехода к хаосу.
Таблица 1. Перечень основных путей перехода к хаосу
Описание функций, полученных в рамках теории детерминированного хаоса.
Во всех вышеперечисленных экспериментах, в которых наблюдался хаос и различные виды перехода к нему, присутствовала возможность проведения достаточного числа наблюдений как при плавно изменяющихся, различных значениях внешних управляющих параметров, так и при одних и тех же. При работе же с финансовыми рынками такая возможность, естественно, полностью исключена. Можно выявить достаточно полный набор критериев, оказывающих в данный момент влияние на некоторый финансовый инструмент, и разработать общее правило, согласно которому из этих критериев будут формироваться внешние параметры. Но из-за постоянного, хаотичного изменения критериев, а соответственно и управляющих параметров, для получения результатов, наглядно доказывающих, что действительно данная система является хаотической, при переходе к хаосу наблюдаются следующие явления и систему с достаточной точностью можно описать следующей моделью, требуется значительное время наблюдения. И тут возникает следующее серьезное осложнение: модель, описывающая поведение цен на финансовых рынках, может претерпеть сильное изменение даже за очень короткий промежуток времени.
Для всех функций подразумевается, что y Î [0, 1]. Т.о. в общем случае необходимо предварительное преобразование данных.
Функции, полученные на основе (9):
В общем случае можно представить как
- yn+1 = f(yn, x, a``) = yn* f1(x, a``) - yn2 * f2(x, a``), (16)
где f1(x, a``) и f2(x, a``) везде положительны.
Область значений yn+1 ограничена интервалом:
[0, max{f1(x, a``)}/min{ f2(x, a``) }], если max{f1(x, a``)}/min{ f2(x, a``) }<1, в противном случае правая граница равна [0, 1].
В качестве функций f(x, a``) предложены следующие:
m
- f(x, a``) = (S(a``i * xi))v, (17)
i=1
где v - некоторая четная, целочисленная, большая нуля константа;
m
- f(x, a``) = c1 / (c2 + (S(a``i * xi))v), (18)
i=1
где v, с1, c2 - некоторые константы, v - четная, целочисленная и большая нуля, с1>0, c2>0;
m
- f(x, a``) = c1 / (LN(c2 + (S(a``i * xi))v)) + c3), (19)
i=1
где v, с1, c2, c3 - некоторые константы, v - четная, положительная и целочисленная, с1>0, c2>=1, c3>0;
m
- f(x, a``) = c / [1 + EXP(-S(a``i * xi))], (20)
i=1
где с - некоторая константа, большая нуля.
Функции, полученные на основе (11):
В общем случае можно представить как
- yn+1 = f(yn, x, a``) = f1(x, a``) + yn* f2(x, a``) + yn2* f3(x, a``), (21)
где область значений f2(x, a``) и f3(x, a``) положительна.
Левая граница области значений yn+1 равна min{f1(x, a``)}, если min{f1(x, a``)>0, и 0 в обратном случае; правая граница равна max{f1(x, a``)}+max{f2(x, a``)}+max{f3(x, a``)}, если max{f1(x, a``)}+max{f2(x, a``)}+max{f3(x, a``)}<1 и 1 в обратном случае.
Здесь для реализации f2(x, a``) и f3(x, a``) предложены функции (17)-(20), а для реализации f1(x, a``):
m m
- f(x, a``) = [EXP(S(a``i * xi)) - с1] / [EXP(S(a``i * xi)) + с2], (22)
i=1 i=1
где с1 и c2 - некоторые константы, большие нуля;
m
- f(x, a``) = COS(S(a``i * xi)), (23)
i=1
m
- f(x, a``) = SIN(S(a``i * xi)). (24)
i=1
Функции, полученные на основе (15):
В общем случае можно представить как
- yn+1 = f(yn, x, a``) = f1(x, a``) - yn* f2(x, a``) + yn-1* f3(x, a``), (25)
где область значений f1(x, a``) и f2(x, a``) положительна, а |f3(x, a``)| < 1.
Левая граница области значений yn+1 равна min{f1(x, a``)} - max{ f2(x, a``) }, если min{f1(x, a``)} - max{ f2(x, a``) } > 0, и 0 в противном случае; правая граница равна max{f1(x, a``)} + max{ f3(x, a``) }, если max{f1(x, a``)} + max{ f3(x, a``) } < 1 и 1 в противном случае. Здесь для реализации f1(x, a``) и f2(x, a``) предложены функции (17)-(20), а для реализации f3(x, a``) - (22) при c1=c2=1.
В любом случае, кроме всех перечисленных требований к функциям f1(x, a``), f2(x, a``) и f3(x, a``), они должны быть определены таким образом, чтобы область значений f(yn, x, a``) охватывала все возможные для данной выборки значения y.
Результаты применения моделей, полученных в рамках теории детерминированного хаоса.
На первый взгляд возникают трудности с представлением в виде данной нейронной сети моделей, описанных в 4. Но ведь все их можно представить так, что каждая функция нелинейного преобразователя в общем случае еще умножается на некоторую константу, являющуюся элементом вектора результатов нелинейного анализа, возведенного в некоторую степень. Алгоритмы обучения сети, построенной с помощью таких моделей, мало чем отличаются от предложенных для стандартной реализации нейронной сети.
За время эксплуатации итоговая погрешность прогноза для сетей, реализующих традиционные модели (в нашей системе реализована двухслойная сеть с произвольным числом нейронов, число которых за время эксплуатации было не более 10), не превышала:
1) для рынка облигаций при прогнозировании цен 0,3%, доходности - 2%;
2) для рынка акций при прогнозировании цен 1,5%;
3) для валютного рынка -1,8%.
А при применении моделей детерминированного хаоса погрешность не превышала:
1) для рынка облигаций при прогнозировании цен 0,25%, доходности - 1,4%;
2) для рынка акций при прогнозировании цен 1,1%;
3) для валютного рынка -1,3%.
При чем в следствии упрощения архитектуры сети удалось значительно уменьшить время прогноза.
На рисунке 4 представлен график нелинейной составляющей
цены акции РАО ЕЭС (обычная линия), пунктирной линией показана аппроксимация с
помощью традиционной модели, крестиками отмечены точки, в которых аппроксимация
с помощью моделей детерминированного хаоса дает значительно лучший результат.
Выводы.
Все рассмотренное выше подтверждает, что применение специализированных моделей, построенных в рамках теории детерминированного хаоса, в нейронных сетях для прогнозирования тенденций финансовых рынков приводит к улучшению качества прогноза. И позволяет предположить, что дальнейшее изучение данного вопроса является весьма перспективной задачей. Данная статья в состоянии только сделать краткий обзор вопроса создания моделей детерминированного хаоса применительно к финансовым рынкам.


