Non riesco a districarmi nel labirinto del codice, ma vorrei confrontarlo.
Preventivo iniziale
Abbiamo le seguenti varianti di lisciatura:
Risultato dello spianamento
Equazione di regressione:
eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)
Stima dell'equazione di regressione
| Variabile | Coefficiente | Stand.osh. | Statistica t | probabilità |
| EURUSDSM(-1) | 0.759607 | 0.049127 | 15.46225 | 0.0000 |
| REND | 0.000207 | 5.79E-05 | 3.577804 | 0.0005 |
| C | 0.314884 | 0.065276 | 4.823886 | 0.0000 |
Quadrato R = 0,788273
Errore standard della regressione = 0,015172
Dai dati ottenuti, notiamo che
tutti i coefficienti di regressione sono significativi (la probabilità che siano uguali a zero è pari a zero)
un R-quadro piuttosto alto (ma non altissimo), che indica che la regressione spiega il 78% della varianza
l'errore standard è di 151 pip. Si tratta di una cifra enorme.
Possiamo fidarci dei numeri risultanti?
Io non mi fiderei, dato che secondo Jarque-Bera la probabilità che la serie smussata abbia una distribuzione normale è del 31%.
Facciamo una previsione:
L'errore di previsione non è molto lontano dall'errore di regressione e supera i 100 pip.
Osserviamo il grafico dell'errore di previsione:
Ebbene, questo è un finale completo: l'errore è variabile, il che significa che il comportamento futuro della previsione è sconosciuto!
Per scoprirne il motivo, osserviamo la correlazione dei coefficienti dell'equazione di regressione:
Possiamo considerare che i coefficienti c(1) e c(3) sono correlati quasi al 100%.
La mia conclusione è che non possiamo utilizzare lo smoothing esponenziale per la previsione.
Perché abbiamo risultati diversi?
Mi sembra ovvio che i parametri ottimali che avete trovato non sono altro che un banale adattamento. La regressione stessa è senza speranza, i suoi coefficienti sono correlati.
Mi sembra evidente che i parametri ottimali che avete trovato non sono altro che un banale adattamento. La regressione stessa è senza speranza, i coefficienti in essa contenuti sono correlati.
Grazie per il suo interesse per l'articolo.
Per favore, chiarisca cosa intendeva dire? Quali risultati non convergono e quali sono i parametri ottimali?
Per favore, chiarisci cosa intendi dire?
Mi scusi, lei dice che si può usare, ma la mia conclusione è che non si può.
Cosa usare e perché?
In conclusione, va notato che i modelli di smoothing esponenziale in alcuni casi sono in grado di produrre previsioni altrettanto accurate di quelle ottenute con modelli più complessi, confermando così ancora una volta il fatto che il modello più complesso non è sempre il migliore.
La mia conclusione è che lo smoothing esponenziale non dovrebbe essere utilizzato per le previsioni.
Quali sono le vostre domande e perché le ponete?
La mia conclusione è che non è possibile utilizzare lo smoothing esponenziale per le previsioni.
A cosa si riferiscono le sue domande e perché le pone?
Mi piacerebbe provare a rispondere a qualcosa, ma ho bisogno di conoscere almeno la domanda. Altrimenti dovrò tirare a indovinare e fantasticare.
Cercherò di chiarire ancora una volta.
I modelli di smoothing esponenziale non possono essere utilizzati per prevedere la coppia eurusd, qualche citazione o mai?
P.S..
Nel testo si legge: "Equazione di regressione:eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Perché la regressione, l'articolo parla di modelli di smoothing esponenziale, e c'è un modello diverso, invece di c(3) c'è una variabile casuale con una certa distribuzione e dispersione?
Nel testo: "Equazione di regressione:eurusd = c(1)*eurusdsm(-1) + c(2)*trend + c(3)". Perché la regressione, l'articolo parla di modelli di smoothing esponenziale, e c'è un modello diverso, dove al posto di c(3) c'è una variabile casuale con una certa distribuzione e varianza?
Non funziona, si parla da ciechi a sordi. Rimandiamo.
Complimenti ancora per l'ottimo articolo.
Non funziona, parlare da cieco a sordo. Rimandiamo.
Complimenti ancora per l'ottimo articolo.
Sono molto curioso di conoscere il suo punto di vista sulle previsioni con lo smoothing esponenziale. Ci sono molte cose che proprio non so e sono sempre felice di cercare di scoprire qualcosa di nuovo ad ogni occasione, ecco perché faccio domande.
Se non è troppo disturbo, mi spieghi perché se la distribuzione della sequenza originale (o della sequenza originale lisciata) non è normale, la previsione non può essere attendibile? Oppure ho capito male?
Grazie per i complimenti.
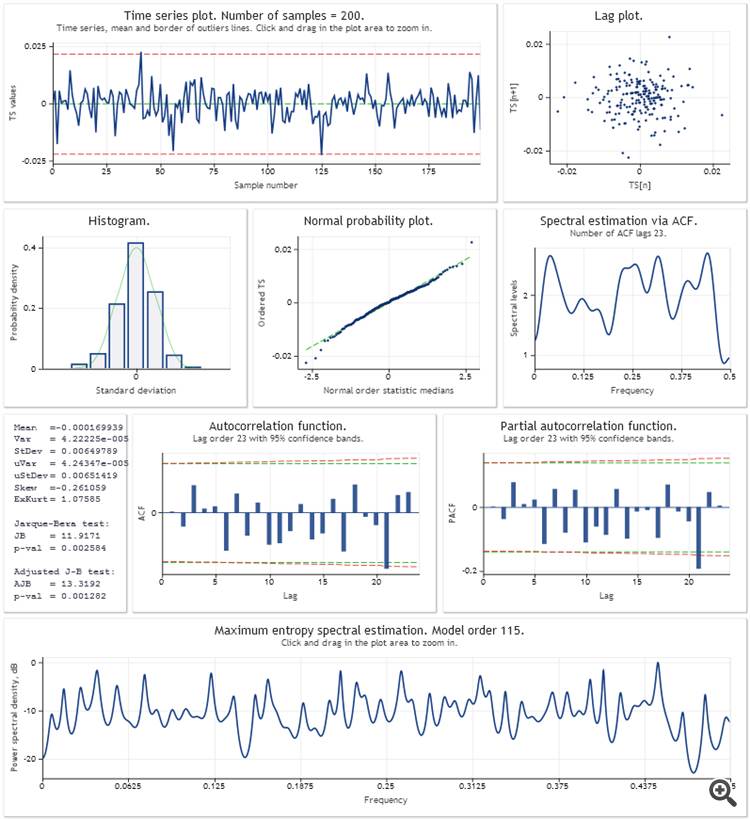
Ecco un'analisi dell'errore di previsione one step ahead per il modello di crescita lineare additivo con smorzamento. I parametri del modello sono stati ottimizzati utilizzando un campione degli ultimi 200 valori di USDJPY,M1. Come nello script Optimisation_Test.mq5 dell'articolo.
https:// www.mql5.com/ru/articles/292
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Il nuovo articolo Previsione di serie temporali mediante livellamento esponenziale è stato pubblicato:
L'articolo permette al lettore di familiarizzare con i modelli di livellamento esponenziale utilizzati per la previsione a breve termine delle serie temporali. Inoltre, tocca le questioni relative all'ottimizzazione e alla stima dei risultati di previsione e fornisce alcuni esempi di script e indicatori. Questo articolo sarà utile come prima conoscenza dei principi di previsione sulla base di modelli di livellamento esponenziale.
Con ogni nuova barra, l'indicatore trova i valori ottimali dei parametri del modello, effettua calcoli nel modello per un dato numero di barre NHist, costruisce una previsione e definisce i limiti di confidenza della previsione.
L'unico parametro dell'indicatore è la lunghezza della sequenza elaborata, il cui valore minimo è limitato a 24 barre. Tutti i calcoli nell'indicatore sono effettuati sulla base dei valori open[]. L'orizzonte di previsione è di 12 barre. Il codice dell'indicatore IndicatorES.mq5 e il file CIndicatorES.mqh si trovano alla fine dell'articolo nell'archivio Files.zip.
Autore: Victor